Оценка эффективности лазерной системы управления направлением разлета поражающих элементов снаряда при поражении воздушных целей

ник (МФП), блок оценки дальности до цели, блок оценки угловых координат, блок определения угла сближения, при котором должна формироваться команда на отстрел. В процессе полета снаряда и его вращения вокруг своей оси со скоростью n ( t ) полупроводниковый лазер формирует в направлении цели непрерывное лазерное излучение, которое, отражаясь от АКП, попадает на вход матричного фотоприемника в виде импульса оптического излучения. При этом конструктивное размещение ППЛ в снаряде и формируемое лазерное излучение с заданной расходимостью луча с учетом вращения снаряда вокруг своей оси должны обеспечивать угловой рабочий сектор 2 α уст (где α уст – конструктивно установленный на снаряде угол отстрела поражающих элементов). По принимаемым матричным фотоприемникам в моменты времени t 1 и t ₂ импульсам (рис. 1) производится оценка текущей дальности до АКП (от снаряда) D 1 и D ₂ [5], измерение текущих угловых координат на АКП (относительно снаряда) а 1 , а ₂ [6-8] и определение угла сближения, при котором должна формироваться команда на отстрел.

Определение момента подрыва боевой части снаряда

Ограничения и допущения, принимаемые при разработке и оценке эффективности данного способа:

• 1.    Стрельба (поражение) осуществляется на встречных курсах.

• 2.    Значения скоростей снаряда и АКП, а также период оборота (вращения) снаряда постоянны.

• 3.    Минимальное количество измерений – 2.

• 4.    При попадании АКП в зону активной локации системы должно выполняться условие: n(t ) • T > 2, где T - период оборота (вращения) снаряда.

С учетом вышесказанного скорости изменения угла сближения и дальности (расстояние от ППЛ снаряда до АКП) можно представить в виде отношений:

а - а а = 2    1

T

D & = D - D

T

где а 1 , а ₂ - угловые координаты АКП (относительно снаряда), измеренные в моменты времени 1 1 и 1 ₂ соответственно; D 1 , D ₂ - дальности до АКП, измеренные в моменты времени 1 1 и 1 ₂ соответственно.

Введем в рассмотрение время инерционности формирования взрыва τ n и скорость полета облака поражающих элементов и _пэ .

АКП

Рис. 1

Тогда угол сближения, при котором должна формироваться команда на отстрел,

a

( к ) от

^а уст

a -a (D a2 a1 пэ

I + T

T I U пэ

где α_уст – конструктивно установленный на снаряде угол отстрела поражающих элементов; D пэ – дальность полета поражающих элементов от снаряда до АКП.

Дальность полета поражающих элементов от снаряда до АКП D_пэ можно определить как

I

Dпэ = D2 + D(t3 - t2), где 13 - момент времени формирования облака поражающих элементов.

Если последнее измерение дальности было выполнено в момент времени 1 ₂, а 1 ₃ - 1 ₂ = T, то

•                                                                     е

D_пэ = D 2 + D ( t з — 1 2 ) = D 2 + DT = 2 D 2 — D i .

С учетом выражений (1), (3) и зависимости а и D от времени получим следующее соотношение:

( к )

от        уст

^{2 D} ( t ) - ^D ( t - T ) _{+ т} ) .         ^ипэ              п )

позволяющее, задаваясь параметрами снаряда, рассчитывать по результатам оценки текущих дальности и угла сближения по двум текущим измерениям в моменты времени t – T и t угол сближения, при котором должна формироваться команда на отстрел.

При рассмотрении эпизода стрельбы пушечным вооружением вертолета по АКП на встречных курсах проведены расчеты для следующих исходных данных: скорость снаряда υ c = 1000 м/с; скорость АКП υ a = 250 м/с; дальность выстрела 500 м; ошибка прицеливания 0,5 град; υ пэ = 2000 м/с; τ п = 0,01 с; α уст = 60 град; T = 4 мс.

На рис. 2 представлены графики зависимостей угла сближения, при котором должна формироваться команда на отстрел, и текущего угла сближения снаряда с целью от времени.

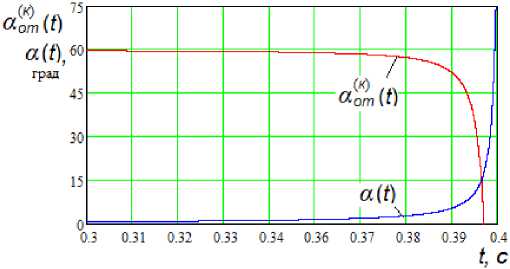
Рис. 2

В соответствии с полученными результатами угол сближения, при котором должна формироваться команда на отстрел, при вышеуказанных исходных данных должен быть равен 15 град, а время отстрела – 0,397 с (пересечение зависимостей на рис. 2).

Задача прогнозирования угла сближения снаряда и АКП

Однако очевидно, что расчеты с использованием выражения (4) будут давать существенные ошибки, обусловленные значимым увеличением скорости изменения угла сближения а ( t ) по мере приближения снаряда к цели. Поэтому для повышения точности определения угла сближения а от ) ( t ) необходимо уменьшение периода формирования зондирующих импульсов ППЛ T . При этом существуют определенные ограничения в возможности уменьшения периода формирования зондирующих импульсов ППЛ T , обусловленные периодом (оборота) вращения снаряда и его конструкционными особенностями. Поэтому возникает задача прогнозирования угла сближения a ( t ).

Для решения этой задачи примем допущение о том, что ошибка прицеливания на протяжении полета снаряда остается постоянной (т.е. траектории полетов снаряда и АКИ параллельны). Тогда, решая несложную геометрическую задачу, получим следующее соотношение:

^{d a} (t ) dt

1 dD ( t ) D ( t ) dt

• tg a (t ).

Решая данное дифференциальное уравнение для начальных условий a(t ₀), D(t ₀), где t ₀ - момент выстрела, получим следующее выражение для прогноза угла сближения снаряда и АКП:

« пр ⁽ t ) = arcsin

f sin a ( 1 0 ) • D ( 1 0 )

I   DW

Ввиду того, что траектория снаряда нелинейная, возникают расхождения полученной прогнозной зависимости с реальной a(t ) (особенно на конечном участке, рис. 3). Кроме того, необходим также прогноз дальности D ( t ).

Для аппроксимации угла сближения по зондирующим импульсам ППЛ с фиксированным периодом T (t > t k ) может быть получено следующее выражение:

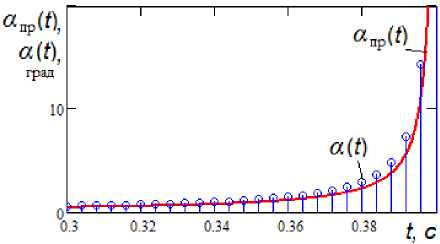
Рис. 3

а пр ( t ) = arcsin <

D (t k ) +

sin ^{a (} t k ) D ⁽ t k ) __________

D ⁽ t k ) - D ⁽ t k "  T ) ( t - t k )

где t k = 0, T, 2 T... - время приема зондирующих импульсов; t - текущее время.

Результаты расчетов с использованием выражения (7) представлены на рис. 4.

Прогнозирование угла сближения a(t ) с учетом его аппроксимации в текущий момент времени (выражение (7)) позволяет рассчитывать время отстрела снаряда следующим образом:

t np = t n - ~ - Т п ,                                                           (8)

U где tn - прогнозируемое время поражения цели при a(t) = ауст, тп = 0 и тпэ = Dпэ / ипэ = 0 (рис. 5).

Из выражения (7) получим tn = tk + T

^{D (} t k ) [ sin ^{a (}t k ) - sin ^а уст ] [ D ( t k ) - D ( t k - T ) ] sin а уст ■

В выражении (8) дальность полета поражающих элементов от снаряда до АКП в момент подрыва снаряда может быть определена следующим образом:

D пэ ( t np ) = D ( t k ) + D ( t k ) D ( t k T ) ( t np ~ tk )■                                    (10)

Решая систему уравнений (8), (9), (10), окончательно получим выражение для определения времени подрыва снаряда на основе прогноза дальности до цели и угла сближения снаряда и цели:

^D(t k ) [ sin ^{a (}t k ) ^- sin а уст ]   D(t_k )      D ( t k ) - D(t_k - T )

t np ⁽ t k ) =

*‘ ⁺ T [ D ( , . ) - D ( t k -T ) ] sin a„ -⁺t k        T U:,         ^Т п

1 + D ( t k ) - D ( t k - T )                         ■⁽¹¹⁾

T U n,

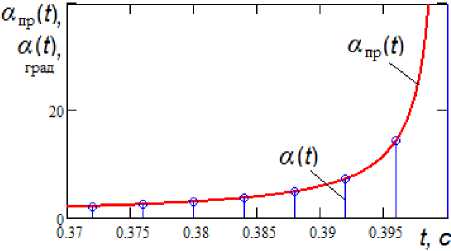
Рис. 4

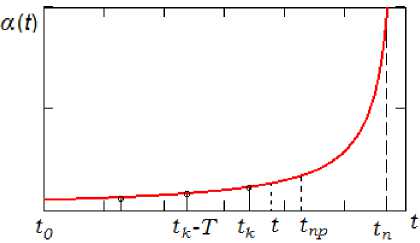
Рис. 5

Fig. 5

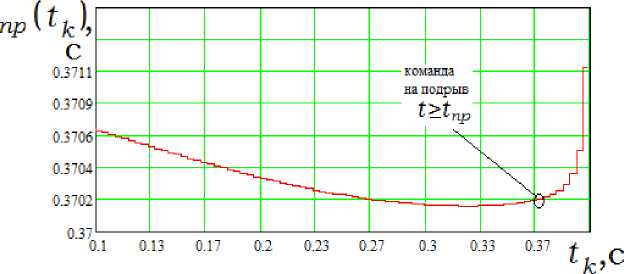
Рис. 6

Fig. 6

В соответствии с выражением (11) для указанных выше исходных данных были произведены расчеты и получен график зависимости прогнозируемого времени подрыва снаряда от времени приема зондирующих импульсов (рис. 6).

На рис. 7 представлена функциональная схема имитационной модели, реализующей вычисления в соответствии с полученным выражением (11).

Имитационная модель процесса определения времени подрыва боевой части снаряда и угла сближения снаряда и цели

Предположим, что ошибки определения угла сближения и текущей дальности в моменты времени t k = 0, T , 2 T … распределены по нормальному закону со среднеквадратическим отклонением (СКО) 0,02 рад и 0,2 м соответственно.

В результате имитационного моделирования (число измерений 500) были получены статистические значения ошибок оценки момента времени, при котором должна формироваться команда на отстрел, представленные в виде гистограммы на рис. 8. При нормально распределенных ошибках оценок угловых координат и дальности математическое ожидание ошибки оценки времени отстрела m Δ t _пр составило – 3,7 · 10^–3 с, а СКО σ Δ t _пр – 4,5 · 10^–3 с.

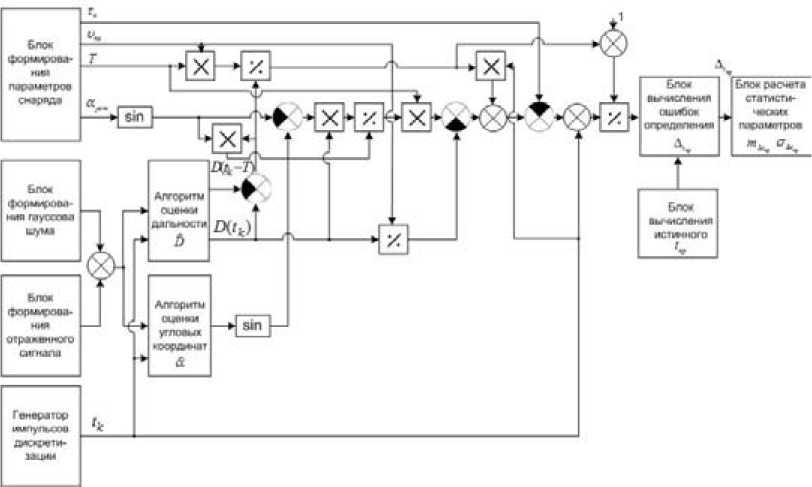
Рис. 7

Fig. 7

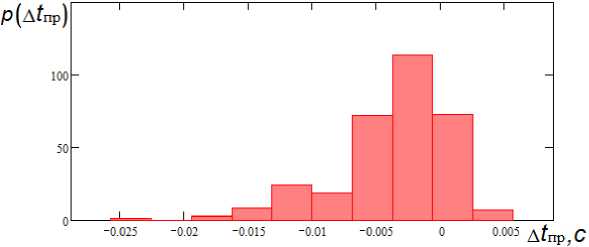
Рис. 8

Fig. 8

Заключение

Таким образом, обоснован способ поражения авиационных комплексов перехвата пушечным вооружением вертолета с использованием снаряда с лазерной системой управления направлением разлета поражающих элементов. Получено выражение для определения времени подрыва снаряда на основе прогноза дальности до цели и угла сближения снаряда и цели. Разработана имитационная модель оценки момента времени, при котором должна формироваться команда на отстрел поражающих элементов в направлении цели. Произведена оценка эффективности предложенной лазерной системы управления.