Оценка эффективности нанесения ущерба групповой воздушной цели без учета противодействия противника

Основным способом уничтожения авиации противника в воздухе является воздушный бой. Наличие в составе авиационных эшелонов ударных тактических истребителей с увеличенным боевым радиусом, оснащенных управляемым оружием класса «воздух – воздух» большой и средней дальности, создает угрозу их массового проникновения к объектам оперативно-стратегического назначения, что обусловливает необходимость первоочередной борьбы с воздушным противником на дальних подступах путем ведения дальних групповых воздушных боев.

Проанализировав назначение, состав и алгоритмы функционирования радиоэлектронной системы управления истребителем и ракетами класса «воздух – воздух» с активно-пассивными головками самонаведения (далее – ГСН), можно сделать вывод, что в большинстве случаев методы самонаведения работают для наведения ракет на одиночные

Оценка эффективности нанесения ущерба групповой воздушной цели без учета ...

Аюш Карам Хасан адъюнкт кафедры авиационного вооружения и эффективности боевого применения, Военный учебно-научный центр Военно-воздушных сил «Военно-воздушная академия имени профессора Н.Е. Жуковского и Ю.А. Гагарина», город Воронеж. Сфера научных интересов: повышение эффективности группового применения управляемых авиационных ракет с активно-пассивными системами самонаведения. Автор более 10 опубликованных научных работ.

воздушные цели и не всегда дополнительно обеспечивают требуемые условия радиолокационного наблюдения отраженных от десяти и более воздушных целей сигналов в бортовой радиолокационной станции (РЛС) летательного аппарата. Следовательно, методы самонаведения ракет не являются оптимальными и не обеспечивают минимальный промах относительно элементарной цели из состава групповой [1].

Расчет математического ожидания количества управляемых авиационных ракет класса «воздух – воздух» для нанесения необходимого ущерба

Чтобы структурно связать частные показатели в интересах получения общей оценки эффективности, на предварительных этапах моделирования разрабатывается сценарий действий в операции. Под операцией понимаются целенаправленные действия, проводимые с использованием различных вариантов сил, средств и способов их действий. Сценарий представляет собой неформализованное описание, отражающее последовательность действий моделируемых сил и средств участников операций. Часто такой сценарий представляется эпизодами, которые формализуются случайными событиями в виде так назы- ваемой марковской цепи, используемой в качестве приема в одноименной теории случайных процессов.

Основным допущением теории марковских процессов, позволяющих описывать войсковую операцию, является предложение о том, что состояние системы на каждом из последующих этапов не зависит от ее состояния на предшествующих этапах и определяется самостоятельно. Финальная вероятность достижения успеха в операции pm может быть определена как произведение вероятностей pi достижения успеха в каждом из составляющих ее фрагментов [2]:

P m = P 1 ^П P 2 ^П P 3 ^П ... ^П P m

^ P m = P 1 ■ P 2 ■ P 3 • ••• • P m                                     (1)

m

^ P m = П Pi, i = 1

где p_m – вероятность поражения всех элементов групповой воздушной цели (далее –

ГВЦ); m – количество элементов ГЦ; p_i – вероятность поражения элемента i .

Если ГЦ является групповой воздушной целью и ее поражение осуществляется управ- ляемыми авиационными ракетами класса «воздух – воздух» типа изделия 180Б, то pi примет фиксированное значение, определяемое параметрами ракеты ( р0 = 0,7 ). Соответственно, соотношение (1) примет вид

m

P m = П P 0

i = 1

m

^ P m = P 0 .

Анализ рисунка 1 показывает, что увеличение количества элементов в ГВЦ приводит к экспоненциальному уменьшению значения вероятности поражения всех ее элементов при равном количестве применяемых ракет, пока значение этой вероятности не достигнет значения, близкого к нулю, для ГВЦ, состоящей из 10 элементов. Следовательно, если в состав ГВЦ входит пять элементов и произведен пуск по этим элементам пятью ракетами, то вероятность поражения такой групповой цели составит 0,17.

Снижение значения вероятности поражения всех элементов ГВЦ при увеличении количества ее элементов является одной из важнейших задач, которую необходимо решить. В настоящее время доступным решением является увеличение количества ракет, предназначенных для уничтожения каждого элемента.

Величина p0 называется вероятностью поражения цели при пуске одной ракеты. Если по цели производится пуск ракет, каждая из которых поражает цель с вероятностью pn , то вероятность поражения цели ракетами без учета ущерба, наносимого каждой ракетой, можно определить по формуле

Pn = 1 -(1 -P0)n , где n – количество ракет, выпущенных по одному элементу ГВЦ. Тогда отношение (2) принимает вид

[ m

^{1 - (1 -} P 0 ) ] .

При учете важности элемента m предыдущее соотношение принимает вид

Оценка эффективности нанесения ущерба групповой воздушной цели без учета ...

p m

1 - (1 - p -) " k e

m

> 1 при k_e <  p ₀

1 ^пр^и k e = p о

недопустимый недопустимый

истр

Pm = 1 p m

Pm ^ПР^и k e = ¹

бомб p при ke > 1

малоеажный ёе мент >, без учета еажности еажныйэлемент

истр где ke - коэффициент важности; p - вероятность поражения элемента групповой цели - истребителя; p- вероятность поражения элемента групповой цели - бомбардировщика.

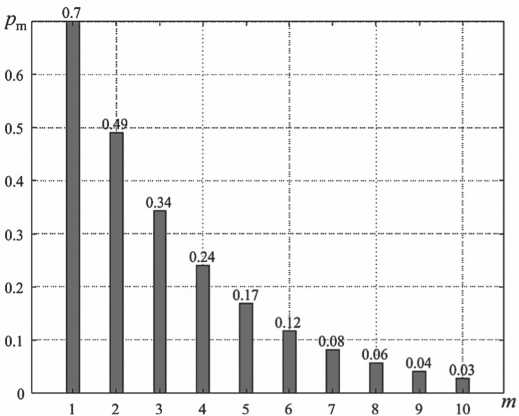
Рисунок 1. Зависимость вероятности поражения всех элементов ГВЦ от количества элементов в ГВЦ

Из соотношений (4), (5) находится вероятность поражения всех элементов ГВЦ ( p ), состоящей из m элементов, при распределении на каждый элемент n ракет, которая представлена графически на рисунке 2.

Анализ рисунка 2 показывает, что вероятность поражения всех элементов ГВЦ увеличивается, когда количество ракет, применяемых для поражения каждого элемента ГВЦ, растет. Например, для поражения 8 элементов ГВЦ при одной ракете по одной цели вероятность p = 0,05; для поражения 8 элементов ГВЦ при пуске трех ракет ( n = 3) по одной цели p = 0,8 и т. д. (Рисунок 2). Проведенный анализ позволяет обосновать число ракет (не более 4) по каждому элементу ГВЦ.

Увеличение количества ракет в зависимости от решаемой боевой задачи связано:

• •    с нерациональным и экономически невыгодным их применением;

• •    сложностью в достижении боевого превосходства в проводимой воздушной операции при наведении большого количества ракет и самолетов-носителей и управлении ими;

• •    мероприятиями при выполнении динамического целераспределения ракет по элементам ГВЦ.

0.2 0.1

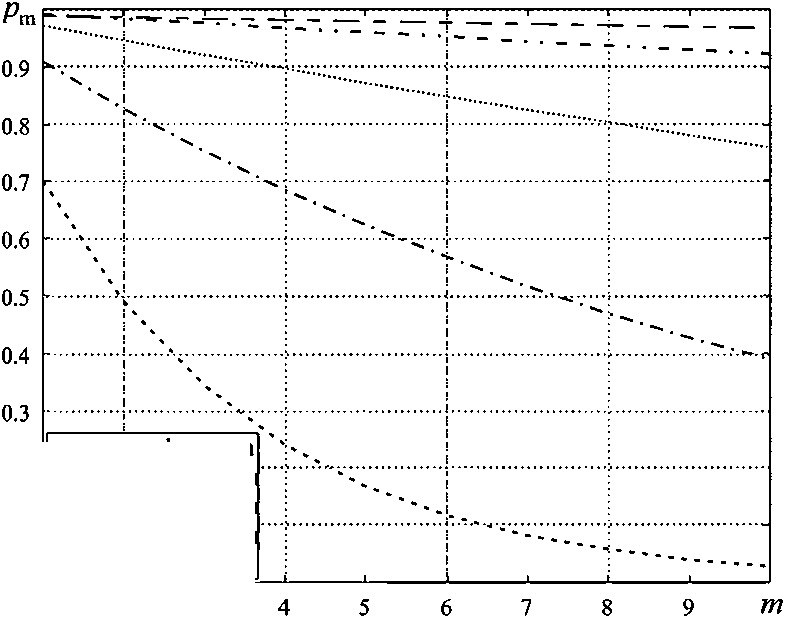
1        2        3

......./7=1 ракета ------/7=2 ракеты ................/7=3 ракеты: -----/7=4 ракеты:

- /7=5 ракет

Рисунок 2. Зависимость вероятности поражения всех элементов ГВЦ от количества элементов в ГВЦ при увеличении количества ракет, распределяемых по каждому элементу

Цели распределяются по элементам групповой воздушной цели таким образом, чтобы на каждый элемент приходилось определенное количество ракет с учетом того, что эти элементы ГВЦ отличаются друг от друга по оценкам важности и характеристикам (возможности элемента ГВЦ воздействовать средствами радиоэлектронного, огневого и маневренного противодействия). В случае ГВЦ 8 истребителей обеспечивают прикрытие двух бомбардировщиков.

Бомбардировщик (В-52) воспринимается как большой (ЭПР составляет 100 м ² ), маломаневренный и большой важности, истребитель (F-16) – как малый (ЭПР примерно 12 м ² ), маневренный и менее важный [3].

Из этого следует важность процесса ранжирования выбранных воздушных целей. Поэтому разработан способ ранжирования целей, учитывающий:

• •    степень их важности при воздействии противника;

• •    сформированный ракетный залп, необходимый для поражения ГВЦ с вероятностью не менее 0,9.

Количество ракет в группе определяется в зависимости от количества элементов в групповой цели; характера (учет важности) групповой цели; чем больше число важных элементов в ГВЦ, тем большее количество ракет противодействуют им.

Способы уничтожения ГВЦ будут анализироваться сначала без учета ранжирования элементов в ГВЦ (далее – первый случай ), а затем с использованием способа, учитыва-

Оценка эффективности нанесения ущерба групповой воздушной цели без учета ...

ющего ранжирование важности элементов в групповой воздушной цели (предлагаемый способ, который в дальнейшем будет называться вторым случаем ).

Главной задачей залпа ракет является поражение воздушных целей или предотвращение их прорыва к обороняемому объекту. Под поражением ГВЦ понимается ее уничтожение или нанесение ей такого ущерба, при котором она не в состоянии выполнить свою боевую задачу.

В исследуемом случае имеются две большие цели (2 бомбардировщика) и пять малых элементарных (8 истребителей). Из вышеизложенного понятно, что основная задача защиты от такой ГВЦ состоит в уничтожении двух бомбардировщиков.

Важнейшей числовой характеристикой закона поражения является математическое ожидание (далее - МОЖ) числа попаданий, необходимое для поражения цели ( ® N ).

Рассмотрим модель исследуемого процесса, при которой фиксируются результаты каждого попадания ракеты в картинную плоскость цели и которая прекращается при достижении поражения элементарной цели при N попаданиях.

Рассматриваемый процесс является дискретной однородной цепью марковского процесса, так как объект может находиться в одном из A состояний ( A ( n ) – состояний ущерба от n попаданий ракет). Смена состояний (шаг процесса) осуществляется в фиксированные моменты времени (при попадании). Известны или могут быть вычислены вероятности того, что система (объект поражения), которая до очередного шага была в состоянии p ( n - 1 ) , в результате этого шага перейдет в состояние p ( n ) . Обратный переход невозможен. Переходы системы в возможные состояния составляют полную группу несовместных событий.

Переходные вероятности такого процесса определяются выражением p ( n ) - p ( n - 1 ) . Вероятность того, что в такой «стрельбе» будет ровно N попаданий, равна вероятности непоражения цели предыдущими ( N - 1 ) попаданиями: 1 - p ( N - 1 ) .

По правилам определения МОЖ дискретной случайной величины найдем как

N - 1

toN = S, n [ p ( n )-p ( n-1)] + N [1-p ( N-1)] = n=1

1 - p ( 1 ) - b p ( 0 ) + 2 ■ p ( 2 ) - 2 ■ p ( 1 ) + 3 ■ p ( 3 ) - 3 - p ( 2 ) + ... + ( N - 1 ) - p ( N - 1 ) -

• - ( N - 1 ) - p ( N - 2 ) + N - N ■ p ( N - 1 ) =                                          (6)

• - p ( 0 ) - p ( 1 ) - p ( 2 ) - ... - N ■ p ( N - 1 ) + N =

N - 1

• [ 1 - p ( ⁰ ) ] + [ 1 - p ( 1)M1 - p ( ² ) ] + ... + [ 1 - p ( ^N "O^H ¹ - p ( n ) ] ,

n = 0

где to N - МОЖ числа попаданий, необходимое для поражения цели.

Для расчета математического ожидания количества ракет, распределенных по каждому элементу ГВЦ, в первом случае (без учета ранжирования важности элементов) ГВЦ будем рассматривать как группу элементов равной важности, а во втором случае (с учетом важности ранжирования важности элементов) группа элементов ГВЦ будет разделена на две подгруппы. В первую подгруппу войдут наиболее важные элементы цели (2 бомбардировщика), имеющие значение коэффициента важности больше единицы ( кв > 1). Вто- рая подгруппа будет включать в себя наименее важные элементы цели (8 истребителей), которые будут иметь коэффициент важности со значением в диапазоне кв е]p0,1[. Значение коэффициента важности определяется на основании мнения экспертов и результатов многих экспериментов. В исследуемом случае этот коэффициент принимает следующие значения:

k

k

истр

' в бомб

в

= 0,8

= 2,

где к_в р - коэффициент важности истребителя; к_в - коэффициент важности бомбардировщика.

На основании вышеизложенного сформирована таблица 1.

Таблица 1

Расчет математического ожидания количества ракет, распределенных по каждому элементу ГВЦ

Тип случая	Учитывая важность		Без учета важности
Количество групп (бомбардировщики, истребители)	2		1
Количество элементов в группе m	2	8	10
Вероятность уничтожения одного элемента одной ракетой, p 0	0,7	0,7	0,7
Коэффициент важности, к в	2	0,8	1
Математическое ожидание, to N	3,982 * 4	1,793 * 2	2,934 * 3
Количество ракет, необходимое для уничтожения всех элементов, N m	8	16	30
Количество ракет, необходимое для уничтожения ГВЦ, N	24		30

Из таблицы 1 следует, что для поражения всех важных элементов ГВЦ в составе 2 бомбардировщиков и 8 истребителей (нанесение ей ущерба, при котором ГВЦ не в состоянии выполнить свою боевую задачу) необходимо принять следующее решение: для первого случая – применение 30 УРВВ, при котором целераспределение осуществляется по три ракеты на каждую цель; для второго случая – применение 24 УРВВ, при котором целера-спределение осуществляется по четыре ракеты на каждую важную цель (бомбардировщик), а на каждую менее важную цель (истребитель) – по две ракеты.

Оценка эффективности использования метода, учитывающего ранжирование важности элементов в ГВЦ

Изучив числовые характеристики закона поражения – МОЖ числа попаданий, необходимое для поражения цели, вероятности попадания в цель, можно перейти к вопросу оценки эффективности.

Если закон распределения случайных отклонений не меняется от выстрела (пуск ракеты) к выстрелу (например, не меняется дальность), то вероятность попадания остается постоянной ( p ₀ ). В этом случае выстрелы можно представить последовательностью независимых испытаний, в которых результатом каждого из испытаний может быть один из двух исходов (попал / не попал), и вероятность поражения одной ракетой является фик-

Оценка эффективности нанесения ущерба групповой воздушной цели без учета ...

сированной величиной. Такие опыты называются схемой испытаний Бернулли. В изучаемом случае определим вероятность поражения ( M = 10 ) элементов при n ракетах.

Если выполняются эти условия, то вероятность определенного числа попаданий при независимых выстрелах при неизменной вероятности попадания подчиняется биноминальному закону распределения [4]

mm   М-т pMm = CM - P -(1 -P)    ,                           (8)

где pM,m - вероятность уничтожения m элементов из ГВЦ (m = 10); CM — биномиальный коэффициент (число сочетаний); M – количество всех элементов ГВЦ; m – количество уничтоженных элементов ГВЦ; (M - m) - количество элементов ГВЦ, которые не были уничтожены.

Действительно, m попаданиям и (M - m) промахам соответствует произведение ве роятностей pm -(1 -p)М т , которое должно быть умножено на число сочетаний из M по m, чему соответствуют все возможные случаи m попаданий, различающиеся хотя бы одним номером (в общей последовательности ракет) попавших ракет. Биноминальные коэффициенты обычно табулированы и определяются выражением

C

m

M =

M !

m ! ( M - m ) !

Поскольку число попаданий подчинено биноминальному распределению, МОЖ числа уничтоженных элементов наиболее важных ГВЦ определяется следующим образом [4]:

M

W ( m ) ⁼ ^ m - P ( m ) , m = 0

где W ( m ) - математическое ожидание количества уничтоженных элементов наиболее важных ГВЦ.

МОЖ количества уничтоженных ГВЦ дает точную оценку эффективности поражения цели [2].

На основании вышеизложенного представим табличные значения МОЖ количества уничтоженных важных элементов ГВЦ (Таблица 2).

Таблица 2

Расчет математического ожидания количества уничтоженных важных элементов ГВЦ

Первый случай					Второй случай
(без учета ранжирования важности элементов в ГВЦ)					(учет ранжирования важности элементов в ГВЦ)
m	m CM	p ( m )	m SДЖ'	важ. / \ p ( тйаж ) л у аиж. у	m	mвaж.	m CM	важ. /       \ p ( m^a ж ) важ
0	1	0	0	0	0	0	1	0
1	10	0	1	0,2394	1	1	2	0,016
2	45	0			2	2	1	0,984
3	120	0			3	–	–	–
4	210	0			4	–	–	–
5	252	0			5	–	–	–
6	210	0,0001			6	–	–	–
7	120	0,002			7	–	–	–
8	45	0,0264			8	–	–	–
9	10	0,211			9	–	–	–
10	1	0,7606	2	0,7606	10	–	–	–
W ( тв« ) = 1,7606 у О^ж .у '					W ( meoЖ ) = 1,9838 у важ . у '

Из таблицы 2 следует, что для расчета математического ожидания уничтоженных важных элементов в ГВЦ ( первый случай ) необходимо рассчитать следующие вероятности p⁸¹” ' ( т_вож . ) (Рисунок 3), то есть значения внутри круговой диаграммы:

• 1.    Вероятность того, когда не уничтожен ни один важный элемент ( m_aM . = 0 , при m = 0 ):

• 2.    Вероятность уничтожения одного из важных элементов ( тваж. = 1, при m = 1|2\ ...|9 ): p8a^(1) = p(1) + p(2) +... + p(9) = 0,2394 .(12)

• 3.    Вероятность уничтожения двух важных элементов ( т_важ = 2 ); этот случай достигается только при m = 10 , когда все важные и неважные элементы цели уничтожены:

p8“'(0) = p(0) = 0 .(11)

p60x(2) = p(10) = 0,7606 .(13)

Расчет МОЖ уничтоженных важных элементов в ГВЦ ( второй случай ) сопрягается с вычислением биномиального коэффициента C^m_M , вероятностями уничтожения важных элементов p ^ea^ ( т_вож ) и выполняются для каждого случая: не уничтожен ни один элемент m_важ = 0 ; уничтожен один элемент и не уничтожен другой т_важ = 1 ; уничтожено два элемента m_8M . = 2 . Напрямую это связано с тем, что важные элементы в ГВЦ были определены (Рисунок 3), то есть значения p^8t™' ( т_вож ) находятся снаружи круговой диаграммы.

Оценка эффективности нанесения ущерба групповой воздушной цели без учета ...

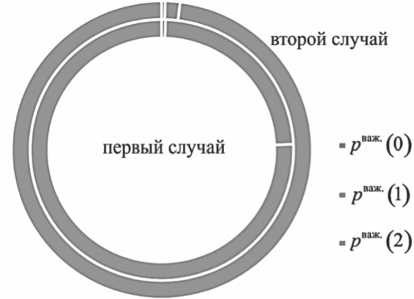
Рисунок 3. Вероятности поражения наиболее важных объектов ГВЦ

Заключение

Таким образом, выполненные исследования (Рисунок 4) показывают, что выполнение расчетов с учетом ранжирования важности элементов в ГВЦ позволит увеличить значение вероятности уничтожения двух важных элементов в ГВЦ (серый цвет), при явном уменьшении значения вероятности уничтожения одного элемента при условии неунич-тожения другого (оранжевый цвет).

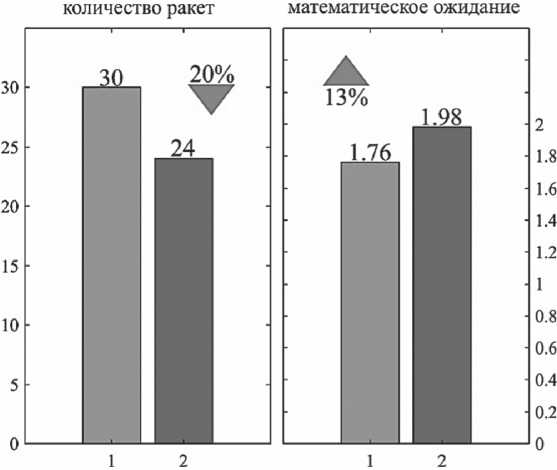
Рисунок 4. Количество ракет, необходимое для поражения ГВЦ, и МОЖ поражения важных элементов ГВЦ при существующих условиях (1) и с учетом ранжирования важности элементов ГВЦ (2)

Рисунок 4 показывает, что снижению потребного наряда ракет на 20 % при уничтожении всех элементов ГВЦ ( М = 10) способствует учет ранжирования важности элементов ГВЦ с ущербом, при котором она не в состоянии выполнить свою боевую задачу.

Учитывая факт уменьшения количества ракет и использование модернизированного метода Т. Саати, можно достичь увеличения значений МОЖ поражения важных элементов ГВЦ с 1,76 до 1,98, то есть прирост эффективности составит 13 %.