Оценка эффективности регионального здравоохранения с применением DEA-подхода и пространственного анализа

Развитие медицинских технологий в сочетании с демографическим переходом, изменившим соотношение между возрастными группами в структуре населения, определяет долгосрочный тренд на увеличение затрат в общественном здравоохранении. В связи с этим в условиях ограниченности ресурсов актуализируется задача создания эффективной системы здравоохранения, обеспечивающей оптимальное использование ресурсов для достижения общественно значимых результатов. Одним из наиболее популярных подходов к количественной оценке эффективности здравоохранения является Data Envelopment Analysis (DEA). Данный подход базируется на фундаментальной работе (Farrell, 1957), в которой была предложена концепция эффективности, а также ориентированный на данные подход к ее измерению. В статьях (Charnes et al., 1978; Banker et al., 1984) представлены базовые модели DEA-подхода. К настоящему моменту инструментарий значительно расширился. Подробный обзор истории развития и современного состояния подхода DEA можно найти в (Zhu, 2014).

В работе (Cantor, Poh, 2017) систематизированы его преимущества и недостатки для оценки эффективности в здравоохранении. Основными преимуществами метода являются следующие: способность работать с множеством показателей ресурсов и результатов одновременно без явного задания функции, отражающей связь между ними; сравнение каждого объекта с другими однородными объектами, в силу чего оценивается относительная, а не абсолютная эффективность; выполнение расчетов без использования информации о ценах. В то же время авторы отмечают следующие недостатки этого подхода: чувствительность результатов к выбору переменных - входов и выходов; неспособность объяснить вариацию оценок эффективности; неработоспособность метода при наличии пропусков в данных. Частично перечисленные недостатки преодолеваются за счет интеграции DEA с другими аналитическими приемами.

В настоящее время подход DEA широко применяется для оценки эффективности объектов здравоохранения различного уровня, включая медицинские учреждения (Федотов и др., 2017), региональные (Авксентьев и др., 2015) и национальные (Radojicic et al., 2019; Perez-Carceles et al., 2017) системы здравоохранения.

Относительно новой идеей в сравнительном анализе эффективности региональных систем здравоохранения является учет пространственных эффектов. Как отмечают авторы в работе (Olejnik et al., 2021), базовый подход DEA позволяет проводить многомерный анализ эффективности однородных независимых центров принятия решений (Decision Making Units, DMUs). Однако в региональных исследованиях предположение о независимости не кажется обоснованным. Соседние территории взаимодействуют друг с другом, что может приводить к возникновению перетоков. В отношении здравоохранения пациенты могут жить в одном регионе, а лечиться в другом, в связи с чем уровень здоровья населения региона может зависеть не только от работы в регионе проживания учреждений здравоохранения, но и от функционирования здравоохранения в соседних регионах. Проникновение новых медицинских технологий также может происходить из регионов-лидеров в первую очередь в близлежащие территории в силу низких транспортных издержек и интенсивных профессиональных и социальных контактов. Для учета пространственных эффектов авторы предлагают модификацию базовой DEA-модели путем включения в нее пространственных лагов ресурсов и результатов.

Целью данного исследования является сравнительная оценка эффективности систем здравоохранения регионов РФ, а также идентификация пространственных эффектов в распределении региональных показателей здравоохранения. В силу того что российские регионы очень неоднородны по размеру и численности населения, в анализ были включены только «европейские» регионы РФ, характеризующиеся небольшими размерами, более высокой плотностью населения, более развитой транспортной инфраструктурой. Перечисленные факторы усиливают межрегиональное взаимодействие и способствуют возникновению пространственных эффектов (Коломак, 2010; Демидова, 2014). В работе выполнен расчет DEA-модели, дающий оценки эффективности и структуру объектов- эталонов, а также определены пространственные эффекты с применением локальных и глобальных одномерных и двумерных индексов Морана.

Теоретические основы исследования

Анализу содержания категории «эффективность здравоохранения» посвящена работа (Lötscher-Stamm, Lenzin, 2024), выполненная в форме разновидности систематического обзора, а именно обзора предметного поля по методологии PRISMA-ScR.

Проведенный анализ 389 релевантных научных статей позволил выделить две разновидности эффективности здравоохранения – производственную и аллокационную. Производственная эффективность предполагает получение максимальных результатов при фиксированных объемах потребления ресурсов или, напротив, заданных результатов при минимальных объемах потребления ресурсов. Аллокационная эффективность – это получение общественно оптимального набора результатов при заданных объемах потребления ресурсов. Производственная эффективность в свою очередь разделяется на четыре подтипа: техническую, ценовую, масштабную, аллокационную. Под технической эффективностью понимается достижение максимального количества результатов при фиксированных объемах потребляемых ресурсов или, напротив, достижение заданных результатов при минимальных объемах потребления ресурсов. Ценовая эффективность предполагает достижение результатов при минимальной стоимости затраченных ресурсов. Масштабная эффективность означает выбор оптимального объема производства. Под аллокационной эффективностью понимается использование такого набора ресурсов, который обеспечивает максимум стоимости результатов.

Согласно исследованию (Lötscher-Stamm, Lenzin, 2024), в большинстве случаев (77,3%) авторы не дают явного определения эффективности, что приводит к путанице и снижает возможности для сравнительного анализа исследований, при этом основной объем работ (99%) посвящен изучению производственной эффективности, в большинстве случаев технической (93%). Метод DEA является наиболее популярным инструментом (74,1% работ), на втором месте – SFA (Stochastic Frontier Analysis, 10,1% исследований).

В научной литературе DEA позиционируется, во-первых, как метод, предназначенный для оценки эффективности, во-вторых, для поиска наилучших практик. Теоретическая концепция эффективности, на которой основан DEA, предложена в работе (Farrell, 1957). Первоначально данная концепция позиционировалась как подход к решению проблемы измерения производственной эффективности, в силу чего DEA «имеет тесные связи» с экономической теорией, в частности с теорией производственных функций (Charnes et al., 1978). Однако общность и гибкость предложенного подхода была осознана очень быстро: уже в работе (Charnes et al., 1981) авторы продемонстрировали применение DEA в области, весьма далекой от экономики, а именно в изучении эффективности социальных программ подготовки детей к обучению в школе. На сегодняшний день DEA нашел применение в самых различных сферах, включая здравоохранение (Кутышкин, Шульгин, 2023), общественную безопасность (Aristovnik et al., 2013), логистику (Suzuki et al., 2011), туризм (Suzuki et al., 2011), общественные финансы (Акиндинова и др., 2024), трансфер-технологий (Дранев и др., 2023) и т. д. Расширение области применения DEA способствовало, во-первых, разработке новых моделей, включая, например, модели с нежелательными выходами (Chen, 2014), двухстадийные модели DEA для работы с многоэтапными процессами (Chen et al., 2010), во-вторых, применению DEA в сочетании с другими аналитическими приемами, чаще всего с регрессионным анализом (Дранев и др., 2023; Afonso, Aubyn, 2011; Husseiny, 2023). Обстоятельный обзор эволюции подхода DEA можно найти в работе (Шапошников, Ратнер, 2023).

Базовое представление о том, как определяется эффективность в рамках DEA-подхода, можно получить, используя графические представления на рис. 1a и 1b.

Оба рисунка соответствуют ситуации, когда объекты, чья эффективность оценивается, используют два ресурса x ₁ и x ₂ и производят один результат y . Кривая S ₁ S ₂ на рисунке 1а представляет собой границу эффективности. Каждая точка на этой кривой показывает, какое минимальное количество ресурса x ₂ требуется для производства единицы результата при фиксированном количестве ресурса x ₁. Все точки, принадлежащие этой кривой, технически эффективны. Каждый из объектов, чья эффективность оценивается, представляется как точка на координатной плоскости, чьи координаты показывают, сколько единиц первого и второго ресурсов использует объект для производства единицы результата.

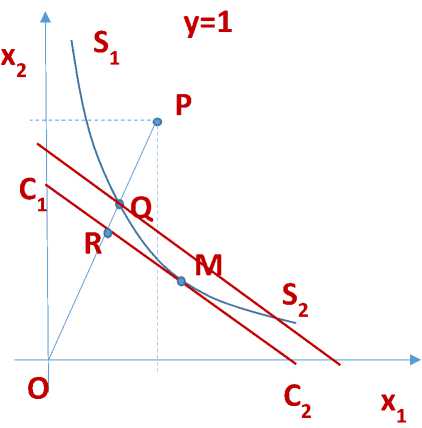
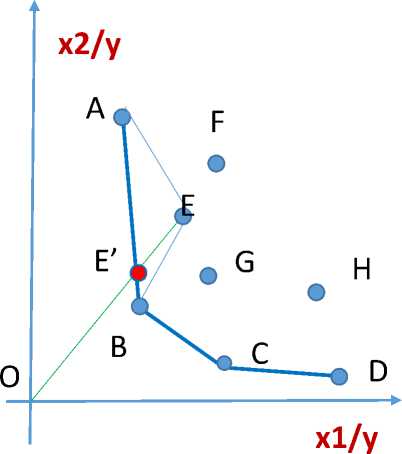
Рис. 1b. Построение границы эффективности в DEA-модели, ориентированной на входы

Рис. 1а. Концепция эффективности по Farrell

Источник: (Farrell,1957).

Если точка лежит на кривой S ₁ S ₂, то объект признается технически эффективным. Если же она расположена правее, как, например, точка P , то объект является технически неэффективным. Мерой его технической эффективности можно считать отношение длин отрезков OQ / OP . Эта величина будет равна единице для технически эффективного объекта и меньше единицы для технически неэффективного. Чем меньше будет эта величина, тем дальше объект от границы эффективности и, соответственно, тем он менее эффективен.

Кроме того, на кривой S ₁ S ₂ существует точка M , соответствующая минимальной стоимости ресурсов, обеспечивающей производство единицы результата (предполагается, что цены на ресурсы фиксированы и одинаковы для всех объектов). Отношение длин отрезков OR / OQ показывает, во сколько раз можно снизить стоимость ресурсов для получения единицы результата, т. е. является мерой экономической эффективности. Мерой общей эффективности является отношение длин отрезков OR / OP . Нетрудно заметить, что общая эффективность может быть найдена как произведение технической и экономической. Также важно отметить, что для измерения экономической эффективности необходимо знание цен на ресурсы, в то время как техническая эффективность определяется без них.

Практическое применение концепции эффективности Farrell затрудняется тем, что граница эффективности практически всегда неизвестна и обосновать ее теоретически крайне сложно. Идея DEA состоит в том, чтобы построить оценку границы эффективности на основе имеющихся данных об объемах потребления ресурсов и производства результатов по пулу однородных независимых объектов. На рисунке 1b координаты каждой точки – это количество первого и второго ресурсов, использующихся для производства единицы результата каждого из объектов пула. Кусочно-линейная кривая ABCD, на которой все точки лежат либо на ней, либо за ней, представляет собой оценку границы эффективности. Объекты, соот- ветствующие точкам A, B, C, D, признаются эффективными. Точки, лежащие за кривой, – неэффективными, например точка E. Отрезок OE пересекает кривую ABCD в точке E'. Отношение длин отрезков OE'/ OE дает оценку технической эффективности объекта, соответствующего точке E. Нетрудно заметить, что точка E' лежит на отрезке AB, следовательно, ее координаты можно представить как линейную комбинацию координат точек A и B. Точки A и B, во-первых, эффективны, во-вторых, наиболее близки к E, т. е. похожи в плане сочетания использования ресурсов среди всех эффективных, поэтому соответствующие им объекты можно рассматривать как «эталоны», или «лучшие практики» для E.

В общем случае, т. е. при любом количестве ресурсов и результатов, задача построения границы эффективности сводится к задаче математического программирования. В силу того что решение таких задач требует значительной подготовки, поначалу метод не получил широкого распространения. Однако с появлением программного обеспечения, автоматизирующего расчеты, количество публикаций с применением DEA стало стремительно нарастать (Hollingsworth, 2008).

Применение DEA для оценки эффективности и поиска наилучших практик в области здравоохранения имеет длительную историю. В относительно старой работе (Hollingsworth, 2008) представлен систематический обзор 317 работ, посвященных оценке эффективности объектов здравоохранения, включая больницы, врачей, программы, службы, а также национальные системы здравоохранения в целом. Согласно этому обзору, 48% исследований использовали DEA, еще 19% базировались на применении DEA в сочетании с регрессионным анализом. Поначалу основной объем исследований был посвящен сравнительному анализу эффективности больниц. Однако в последнее десятилетие вырос интерес к сравнительному анализу эффективности национальных и региональных систем здравоохранения. В силу того что метод DEA базируется на включении в анализ однородных объектов, обычно при изучении национальных систем здравоохранения ограничиваются странами, объединенными географической близостью или членством в каких-либо союзах или объединениях. Например, работа (Afonso, Aubyn, 2011) посвящена эффективности здравоохранения в странах – членах OECD, исследование (Dhaoui, 2019) ограничено странами Ближнего Востока и Северной Африки, работа (Husseiny, 2023) касается эффективности национальных систем здравоохранения в арабских странах.

Работ, посвященных сравнительной оценке региональных систем здравоохранения, относительно немного, однако примеры таких исследований можно найти, например в Словакии (Stefko et al., 2018), Саудовской Аравии (Abdelfattah, Alanazi, 2024), Тайване (Wu, 2023), России (Авксентьев и др., 2015), Китае (Lin et al., 2021), Турции (Manavgat, Demirci, 2020).

Быстрое развитие геоинформационных систем, начавшееся во второй половине XX века и продолжающееся по сей день, способствовало появлению и развитию пространственного анализа, позволяющего исследовать различные закономерности с учетом географического положения, окружения и взаимодействия объектов. Как и в случае с DEA, появление специализированных пакетов и модулей, значительно облегчающих техническую сторону использования инструментов пространственного анализа, привело к резкому увеличению числа научных публикаций с его использованием (Демидова, 2014).

Инструменты пространственного анализа весьма востребованы в современных региональных исследованиях, в том числе в российском научном сегменте. Географические размеры России, а также значительная неоднородность регионов по размерам, плотности населения, природно-климатическим условиям обусловливают одновременно и ценность, и сложность применения инструментов пространственного анализа. В ряде исследований доказано, что экономические закономерности могут формироваться по-разному в западной и восточной части страны. В работе (Коломак, 2010) установлено, что в западных регионах экономический рост в регионе не локализуется в границах территории, а выходит за его пределы, распространяясь на соседние регионы и далее. При этом в восточных регионах экономический рост территории ассоциируется со снижением темпов роста соседних территорий. Автор объясняет это тем, что большие расстояния, низкая плотность экономической активности и инфраструктуры мешают распространению в пространстве положительных влияний экономического роста и приводят к доминированию отрицательных эффектов межрегиональной конкуренции.

Работ, использующих сочетание DEA с инструментами пространственного анализа в исследованиях по эффективности здравоохранения, относительно немного, однако их число растет в последнее время. В работе (Olejnik et al., 2021) наличие пространственных эффектов продемонстрировано на данных региональных систем здравоохранения европейских стран. С применением базовых инструментов пространственного анализа установлено, что существует значимая положительная пространственная автокорреляция по всем показателям, использующимся в качестве входов и выходов, а также по уровню эффективности регионального здравоохранения. Кроме того, выявлено несколько пространственных кластеров, т. е. объединений регионов по уровню эффективности здравоохранения. Также доказано наличие пространственной корреляции между показателями-ресурсами и показателями-результатами, подтверждающей гипотезу о том, что высокий (низкий) уровень ресурсов соседних регионов положительно (отрицательно) сказывается на показателях здоровья населения региона. В работе (Lin et al., 2021) исследуется динамика эффективности здравоохранения в городах одной из провинций Китая. По результатам исследования выявлена положительная автокорреляция по уровню эффективности, а также наличие пространственных кластеров.

Работа (Manavgat, Demirci, 2020) посвящена изучению эффективности здравоохранения в турецких провинциях. Как и в двух предыдущих исследованиях, выявлена положительная пространственная автокорреляция по уровню эффективности.

Материалы и методы

На первом этапе в данной работе выполнена оценка базовой модели DEA (ориентированной на входы, с переменным эффектом масштаба) для оценки эффективности систем здравоохранения российских регионов. Модель, ориентированная на входы, стремится уменьшить потребление ресурсов при сохранении того же уровня результатов. Выбор в пользу модели с переменным эффектом масштаба связан с тем, что регионы РФ значительно отличаются друг от друга, и использование моделей с переменным масштабом обеспечивает сравнение каждой региональной системы с наиболее схожими «аналогами».

С математической точки зрения, оценка DEA-модели сводится к решению задачи на условный экстремум (формулы (1); Zhu, 2014). В представленных формулах (1) y_r j - r -й выход у j -го объекта, г = 1.. s; х^ - i -й вход у j -го объекта, i = 1.. т ; s - количество выходов, m - количество входов, n - количество объектов.

0 * = min 0

ограничения:

• 2)    для каждого неэффективного объекта получить объект-эталон как линейную комбинацию эффективных объектов; эффективные объекты, входящие в объект-эталон с ненулевыми весами (A j ) , наиболее схожи с неэффективным объектом, и их опыт может быть полезен для повышения эффективности функционирования объекта;

• 3)    для каждого неэффективного объекта оценить избыточное потребление ресурсов или недополучение результатов.

На втором этапе выполнялась оценка пространственных эффектов, в качестве инструментов использовались глобальный индекс Морана, локальные индексы Морана (LISA), глобальный двумерный индекс Морана, а также тесты на оценку их статистической значимости (Anselin, 2024). Глобальный индекс Морана является пространственным аналогом коэффициента автокорреляции и рассчитывается по формуле 2:

[ MG

gUS^l^ • fa - X) • fe - ^1 £^ 1 ^ ?=!^ ₍₂₎

Е Г=1 (х_;-х)² /п              ^,()

где:

X j , y j - значения показателей в j -м регионе;

х, У - средние значения показателей;

N – количество регионов;

w^ - элементы взвешивающей матрицы ^W = (Ч х,

^i:

п

7 = 1

^■j ' ^x ij

io

Vr:

h j •y rj — У г0

п j=1

^ j

= 1

^ — 0

Оценка модели, заданной формулами, позволяет:

1) оценить 9 j - эффективность каждого объекта: объект признается эффективным, если 9 * = 1 , если 9 ? <  1 , объект признается неэффективным; чем меньше 9*, тем более неэффективен объект;

Если 1^ма >  - 1/(п- 1) , то имеет место положительная пространственная автокорреляция, т. е. регионы с высоким (низким) значением показателя в основном окружены регионами с высокими (низкими) значениями этого же показателя. И наоборот, если i^MG< - 1/(п -1) , то имеет место отрицательная пространственная автокорреляция, т. е. регионы с высоким (низким) значением показателя в основном окружены регионами с низкими (высокими) значениями этого же показателя. В данной работе глобальные индексы Морана использовались для оценки пространственной автокорреляции показателей входов, выходов и эффективности региональных систем здравоохранения

для проверки гипотезы о наличии значимых эффектов межрегионального взаимодействия.

Локальный индекс Морана, или локальный индекс пространственной автокорреляции (Local Index of Spatial Autocorrelation, LISA), рассчитываемый по формуле (3), интерпретируется так же, как и глобальный, но считается для каждого региона:

_ ^(xi^-x) • ^=1 W ij • (x - ^x) jy^iY^i W^

^{L i} =         S^-X)² /» ■          , ⁽³⁾

где:

X j , y j - значения показателей в j -м регионе;

• х, у - средние значения показателей;

• N – количество регионов;

Wij - элементы взвешивающей матрицы ^W = «X. .

Локальные индексы Морана используются для выявления региональных кластеров, т. е. групп пространственно связанных регионов с низкими или высокими значениями показателя, а также регионов-«выбросов», т. е. регионов с высокими (низкими) значениями показателя, окруженных регионами с низкими (высокими) значениями показателя.

Двумерный глобальный индекс Морана jbvMG является аналогом линейного коэффициента корреляции Пирсона, позволяя оценивать пространственную корреляцию между двумя переменными (формула 4):

[ bvMG _

Е "₌₁ Е "₌₁ wy • (х ₍ - х) • (у - у)/У^ У^^ w j

У^Х-х)2 /п          , где:

X j , y j - значения показателей в j -м регионе;

X, у - средние значения показателей;

N – количество регионов;

Wij - элементы взвешивающей матрицы ^W = «X. .

В данной работе двумерные глобальные индексы Морана использовались для оценки пространственной корреляции показателей-входов с показателями-выходами для проверки гипотезы о том, что высокий

(низкий) уровень ресурсов здравоохранения в соседних регионах способствует формированию высокого (низкого) уровня результатов в данном регионе.

Все описанные индексы Морана базируются на использовании взвешивающей матрицы. В рамках пространственного анализа предложено множество подходов к ее формированию. В рамках данного исследования использовался один из базовых вариантов, а именно матрица соседства «по правилу ферзя». В рамках этого подхода соседними считаются регионы, имеющие хотя бы одну общую точку на границах. Среднее число соседей у включенных в анализ регионов составило 4,45.

Расчеты выполнялись в программе RStudio. Оценка DEA-модели осуществлялась с применением функций пакета deaR, картограммы строились с применением пакетов ggplot и bispdep, матрица весов формировалась с применением функций пакета spdep, индексы Морана рассчитывались с использованием пакетов spdep и bispdep.

Выбор показателей ресурсов и результатов выполнялся «по аналогии» с существующими работами в области оценки эффективности здравоохранения и с учетом доступности данных. В этом отношении значительную ценность представляет работа (Radojicic et al., 2019), в которой выполнен систематический обзор 44 научных статей, использовавших метод DEA для оценки эффективности национальных систем здравоохранения. Согласно этому исследованию, в качестве показателей входов наиболее часто используют удельные расходы на здравоохранение, количество врачей, среднего медицинского персонала, коек, в качестве показателей выходов – продолжительность жизни, младенческую выживаемость/ смертность, выживаемость/смертность в возрасте до 5 лет, потерянные годы жизни с поправкой на инвалидизацию (Disability Adjusted Life Years, DALYs). В настоящем исследовании в качестве показателей-ресурсов в анализ включены, во-первых, количество врачей и среднего медицинского персонала как индикаторы трудовых ресурсов, количество больничных коек как индикатор размера основных фондов, а также уровень финансирования региональной системы здравоохранения из средств бюджетов всех уровней и территориальных фондов обязательного медицинского страхования. В качестве результативных показателей использовались, во-первых, продолжительность жизни и младенческая выживаемость – практически стандарт де-факто в исследованиях по оценке эффективности здравоохранения. Во-вторых, были добавлены еще два индикатора – выживаемость мужчин и женщин в трудоспособном возрасте. Включение этих показателей представляется обоснованным по следующим причинам. Во-первых, значительный разрыв (более 10 лет) в продолжительности жизни мужчин и женщин является специфической особенностью российской демографической ситуации (Родионова, Копнова, 2020). Во-вторых, именно потери населения в трудо- способном возрасте наносят основной социально-экономический ущерб. В-третьих, в значительной мере потери населения в трудоспособном возрасте являются предотвратимыми, в том числе за счет своевременного и качественного медицинского обслуживания. Информационная база исследования сформирована на основе статистических сборников «Регионы России»1, «Здравоохранение в России»2, а также данных, извлеченных из системы ЕМИСС. Массив данных включает показатели за 2022 год по 58 российским регионам, расположенным в Центральном, Северо-Западном, Южном, Северо-Кавказском и Приволжском федеральных округах. Уровень финансирования региональной системы здравоохранения корректировался с учетом различия цен в регионах путем деления на стоимость фиксированного набора потребительских товаров и услуг. В силу того что подход DEA требует, чтобы показатели-ресурсы были

Таблица 1. Описательная статистика

№	Показатель	Краткое обозначение	Min	Q1	Me	Q3	Max	Moran I	p-value
1	Удельные расходы на здравоохранение	Расходы	0,887	1,197	1,305	1,422	1,450	0,4062	<0,001
2	Численность врачей на 10000 чел. населения	Врачи	33,60	42,17	46,40	47,99	53,15	-0,0644	0,7051
3	Число больничных коек на 10000 чел. населения	Койки	43,50	73,35	80,20	79,13	84,62	0,2040	0,007
4	Численность среднего медицинского персонала на 10000 чел. населения	СМП	66,4	92,2	101,5	101,1	108,1	0,3361	<0,001
5	Ожидаемая продолжительность жизни при рождении	ПрЖиз-ни	68,95	71,22	72,09	72,48	73,31	0,4356	<0,001
6	Младенческая выживаемость	МлВыж	992,0	995,0	995,8	995,5	996,2	-0,0446	0,6186
7	Выживаемость мужчин в трудоспособном возрасте	ВыжМТр	987,4	990,1	991,0	991,4	992,6	0,5895	<0,001
8	Выживаемость женщин в трудоспособном возрасте	ВыжЖТр	996,3	997,2	997,7	997,7	998,0	0,5998	<0,001
Примечание: Мин – минимум, Q1 – нижний квартиль, Me – медиана, Q3 – верхний квартиль, Max – максимум, Moran I – глобальный индекс Морана, p-value – уровень значимости. Источник: расчеты автора.

1 Регионы России. URL:

2 Здравоохранение в России. Приложение: информация в разрезе субъектов Российской Федерации. URL:

«чем меньше, тем лучше», а показатели-результаты «чем больше, тем лучше», показатели смертности преобразованы в показатели выживаемости. Описательная статистика по используемым в работе показателям представлена в таблице 1 .

Как следует из таблицы 1, имеет место значительная вариация показателей по регионам. Кроме того, по большинству показателей (кроме двух - численность врачей на 10000 чел. населения и младенческая выживаемость) имеет место значимая положительная пространственная автокорреляция. Аналогичный результат получен в работе по регионам Европейского союза (Olejnik et al., 2021).

Результаты и обсуждение

Оценки эффективности региональных систем здравоохранения приведены в таблице 2 .

Как следует из таблицы 2, 16 регионов оценены как эффективные: г. Москва, г. Севастополь, Ленинградская область, Чеченская Республика, Республика Дагестан, Республика Ингушетия, Республика Адыгея, Чувашская Республика, Вологодская область, Ставропольский край, Кабардино-

Балкарская Республика, Саратовская область, Калужская область, Республика Татарстан, Липецкая область, Удмуртская Республика. Наименее эффективными регионами являются Ненецкий автономный округ, Республика Коми, Мурманская область, Республика Карелия, Архангельская область. Картограмма эффективности представлена на рисунке 2 .

Как видно из рисунка 2, наиболее неэффективные регионы расположены преимущественно в северо-восточной локации, что позволяет выдвинуть гипотезу о роли климатического фактора в эффективности здравоохранения. Теоретически это можно обосновать тем, что показатели здоровья населения, проживающего в неблагоприятных климатических условиях, при прочих равных условиях ниже, вследствие чего оценка эффективности здравоохранения этих регионов занижается. Однако возможны и другие объяснения: на нее оказывают влияние, например, низкая плотность населения и инфраструктуры в этих регионах. В научной литературе есть немало работ, в которых с применением регрессионного анализа выполняется анализ факторов, обусловливающих вариацию эффективности.

Таблица 2. Оценки эффективности региональных систем здравоохранения

№	Регион	Оценка эффективности	Рейтинг	LISA	LISA_p
1	г. Москва	1	1	1,1306	0,1268
2	г. Севастополь	1	1	-0,8966	0,4154
3	Ленинградская область	1	1	-0,3029	0,5423
4	Чеченская Республика	1	1	0,8276	0,1052
5	Республика Дагестан	1	1	0,8773	0,1411
6	Республика Ингушетия	1	1	0,4940	0,4950
7	Республика Адыгея	1	1	0,5830	0,5749
8	Чувашская Республика	1	1	0,3822	0,3852
9	Вологодская область	1	1	-0,8339	0,0222
10	Ставропольский край	1	1	0,7545	0,0294
11	Кабардино-Балкарская Республика	1	1	0,6182	0,2951
12	Саратовская область	1	1	-0,1877	0,6897
13	Калужская область	1	1	0,2260	0,5567
14	Республика Татарстан	1	1	0,1209	0,6913
15	Липецкая область	1	1	-0,8005	0,0627
16	Удмуртская Республика	1	1	-0,4096	0,4570

Окончание таблицы 2

№	Регион	Оценка эффективности	Рейтинг	LISA	LISA_p
17	Московская область	0,9939	2	0,1351	0,6494
18	Ростовская область	0,9805	3	0,2448	0,5036
19	Карачаево-Черкесская Республика	0,9705	4	0,7227	0,1084
20	Республика Марий Эл	0,9660	5	0,0549	0,8611
21	Псковская область	0,9660	6	0,1415	0,6836
22	Краснодарский край	0,9421	7	0,3272	0,1566
23	Владимирская область	0,9416	8	-0,1474	0,5408
24	Смоленская область	0,9366	9	0,1920	0,3069
25	Ульяновская область	0,9216	10	0,1560	0,2510
26	Республика Калмыкия	0,9147	11	0,1192	0,3338
27	Костромская область	0,9014	12	-0,0539	0,4540
28	Калининградская область	0,8926	13	-0,0093	0,8758
29	Республика Мордовия	0,8902	14	-0,0067	0,7992
30	Волгоградская область	0,8898	15	0,0071	0,7701
31	Брянская область	0,8817	16	0,0040	0,6587
32	Тульская область	0,8692	17	-0,0252	0,6709
33	Республика Северная Осетия – Алания	0,8664	18	-0,1730	0,0285
34	Самарская область	0,8641	19	-0,0919	0,3043
35	Тамбовская область	0,8590	20	-0,0023	0,9893
36	Белгородская область	0,8574	21	0,2256	0,1877
37	Новгородская область	0,8565	22	-0,1478	0,2355
38	Республика Башкортостан	0,8488	23	-0,0640	0,6950
39	Ярославская область	0,8457	24	-0,1012	0,4732
40	Пензенская область	0,8357	25	-0,0174	0,9423
41	Оренбургская область	0,8321	26	-0,0912	0,7489
42	Нижегородская область	0,8321	27	0,0210	0,8751
43	Ивановская область	0,8297	28	0,0161	0,9333
44	Тверская область	0,8219	29	-0,2621	0,2532
45	Воронежская область	0,8192	30	-0,1177	0,6033
46	г. Санкт-Петербург	0,8067	31	-0,4141	0,4198
47	Республика Крым	0,7939	32	-0,6734	0,2580
48	Пермский край	0,7880	33	0,6018	0,1540
49	Астраханская область	0,7721	34	-0,1777	0,8263
50	Рязанская область	0,7689	35	-0,1874	0,6334
51	Орловская область	0,7567	36	-0,1757	0,7646
52	Курская область	0,7481	37	0,2408	0,6180
53	Кировская область	0,7338	38	0,2893	0,4471
54	Ненецкий автономный округ	0,7074	39	3,8140	0,0006
55	Республика Коми	0,6590	40	3,3812	0,0004
56	Мурманская область	0,6508	41	4,9178	0,0165
57	Республика Карелия	0,6377	42	1,4761	0,1416
58	Архангельская область	0,6044	43	3,2639	0,0014
Источник: расчеты автора.

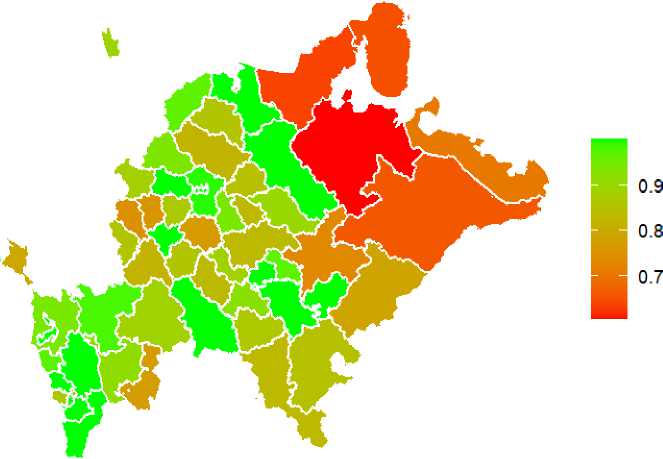
Рис. 2. Картограмма регионов европейской части РФ по уровню эффективности здравоохранения

В работе (Afonso, Aubyn, 2011), посвященной анализу эффективность национальных систем здравоохранения в 44 развитых странах мира, установлено, что значимое влияние на эффективность здравоохранения оказывают социальноэкономические факторы (ВВП на душу населения, темп роста ВВП), а также факторы образа жизни населения (распространенность ожирения и потребления табака). В исследовании (Radojicic et al., 2019) выполняется сравнительный анализ эффективности здравоохранения в 38 странах – членах OECD или BRICS. Согласно этой работе, значимое влияние на уровень эффективности имеет распространенность ожирения. Другие включенные в анализ факторы (ВВП на душу населения, доля населения с высшим образованием, потребление табака, особенности финансирования здравоохранения) оказались незначимыми.

Как видно из рисунка 3, локальный индекс Морана для большинства регионов незначим. Четыре региона (Мурманская область, Ненецкий автономный округ, Архангельская область, Республика Коми) формируют кластер регионов с низкой эф- фективностью. Вологодская область представляет собой регион-«выброс», демонстрируя высокий уровень эффективности в окружении низкоэффективных регионов. Республика Северная Осетия – Алания, также идентифицируется как «выброс», являясь низкоэффективным регионом, окруженным регионами с высоким уровнем эффективности здравоохранения.

Глобальный индекс Морана по уровню эффективности получился равным 0,345 (p < 0,001), что указывает на наличие положительной пространственной автокорреляции по уровню эффективности здравоохранения. Это доказывает существование эффектов перетоков. В целом полученные в этой части результаты хорошо согласуются с расчетами по эффективности регионального здравоохранения в других странах (Lin et al., 2021; Manavgat et al., 2020; Olejnik et al., 2021).

Формирование объектов-эталонов для пяти наименее неэффективных и пяти наиболее неэффективных объектов по модели, ориентированной на выходы, приведено в таблице 3 , востребованность эффективных регионов в формировании эталонов представлена на рисунке 4 .

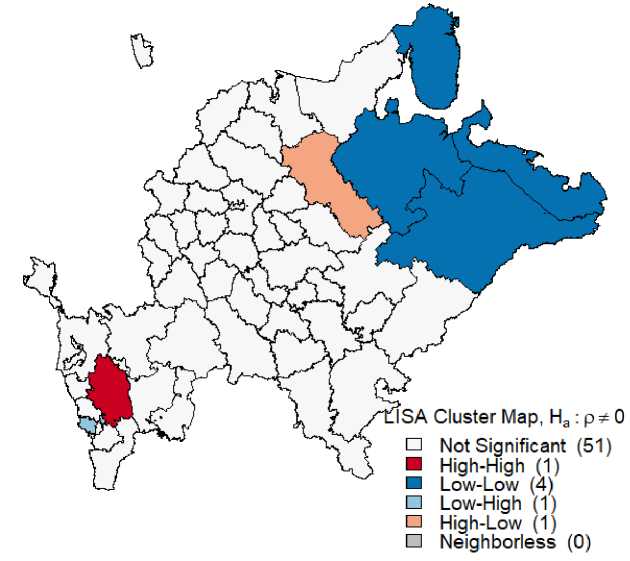
Рис. 3. Картограмма регионов РФ по локальному индексу Морана

Таблица 3. Формирование эталона для неэффективных объектов

Регион	^
Московская область	г. Севастополь (0,12469), Калужская область (0,07360), Ленинградская область (0,59650), Республика Татарстан (0,02999), г. Москва (0,17523)
Ростовская область	г. Севастополь (0,26997), Республика Адыгея (0,01177), Чеченская Республика (0,52101), Ленинградская область (0,19725)
Карачаево-Черкесская Республика	Республика Ингушетия (0,11096), Кабардино-Балкарская Республика (0,12808), Ставропольский край (0,34829), Чеченская Республика (0,23203), Республика Дагестан (0,18065)
Республика Марий Эл	Республика Адыгея (0,36787), Чеченская Республика (0,36630), Вологодская область (0,26583)
Псковская область	Чеченская Республика (0,91304), Вологодская область (0,08696)
Ненецкий автономный округ	Республика Ингушетия (0,19630), Ленинградская область (0,75676), Москва (0,04694)
Республика Коми	Чеченская Республика (0,15519), Ленинградская область (0,21529), Вологодская область (0,62952)
Мурманская область	Чеченская Республика (0,05346), Ленинградская область (0,38524), Вологодская область (0,56131)
Республика Карелия	Республика Ингушетия (0,23794), Чеченская Республика (0,18840), Ленинградская область (0,57366)
Архангельская область	г. Севастополь (0,00942), Республика Ингушетия (0,11002), Чеченская Республика (0,28335), Калужская область (0,17769), Ленинградская область (0,41951)

Источник: расчеты автора.

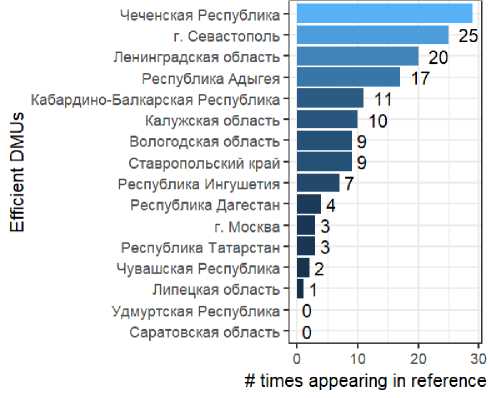
Рис. 4. Востребованность эффективных регионов в формировании объектов-эталонов

Как видно из таблицы 3 и рисунка 4, наиболее часто в объект-эталон с ненулевыми весами входят Чеченская Республика, г. Севастополь и Ленинградская область, наименее востребованы Липецкая и Саратовская области, а также Удмуртская республика. Отметим, что в силу ряда специфических особенностей Чеченская Республика «плохо подходит» на роль эталона для многих регионов РФ, так же как города Москва и Санкт-Петербург, где сосредоточены все федеральные медицин- ские центры и объемы финансирования несоизмеримы по сравнению с другими регионами. Поэтому, если целью применения DEA является именно поиск наилучших практик для определенного объекта, следует более строго подходить к выбору пула однородных объектов, изначально включая в него только «сопоставимые аналоги».

Коэффициенты пространственной корреляции между переменными – входами и выходами приведены в таблице 4 .

Таблица 4. Двумерная пространственная корреляция между показателями – входами и выходами

WX	Y	Двумерный индекс Морана	p-value
Расходы	ПрЖизни	–0,293	< 0,001
Врачи	ПрЖизни	0,003	0,937
Койки	ПрЖизни	–0,327	<0,001
СМП	ПрЖизни	–0,219	0,002
Расходы	МлВыж	0,078	0,246
Врачи	МлВыж	0,075	0,257
Койки	МлВыж	0,019	0,775
СМП	МлВыж	0,034	0,621
Расходы	ВыжМТр	–0,335	<0,001
Врачи	ВыжМТр	0,018	0,778
Койки	ВыжМТр	–0,384	<0,001
СМП	ВыжМТр	–0,264	<0,001
Расходы	ВыжЖТр	–0,357	<0,001
Врачи	ВыжЖТр	–0,024	0,731
Койки	ВыжЖТр	–0,372	<0,001
СМП	ВыжЖТр	–0,209	0,003
Источник: расчеты автора.

Согласно данным, коэффициенты пространственной корреляции между переменными – входами и выходами либо незначимы, либо отрицательны, что идет вразрез с гипотезой о том, что высокий (низкий) уровень ресурсов здравоохранения в близлежащих регионах способствует росту (снижению) показателей-выходов в регионе. В этом отношении наши результаты не согласуются с результатами, полученными в (Olejnik et al., 2021) для европейских регионов. По-видимому, межрегиональные перетоки пациентов в РФ или не столь интенсивны, или происходят не по принципу «ближайшего соседа».

Заключение

Проблема эффективного управления ресурсами здравоохранения является актуальной задачей практически для всех стран мира, в том числе для России. Подход DEA имеет следующие характеристики, обусловливающие его привлекательность для количественной оценки эффективности здравоохранения: теоретическая обоснованность, способность работать с множеством входов и выходов; ориентированность на данные; получение, помимо собственно оценок

эффективности, объектов-эталонов, а также перерасхода ресурсов или недополучения результатов.

В настоящей работе DEA-модель была использована для оценки эффективности систем здравоохранения 58 «европейских» регионов РФ. По результатам расчета 16 регионов были идентифицированы как эффективные, 42 региона – как неэффективные. Среди эффективных регионов наиболее востребованными в качестве эталона оказались Чеченская Республика, г. Севастополь и Ленинградская область.

Дополнение инструментами пространственного анализа позволяет частично преодолеть проблему допущения подхода DEA о независимости однородных центров принятия решений, не выполняющегося в случае, если в качестве таких центров выступают взаимосвязанные регионы. Это и составляет основную научную новизну работы. Согласно нашим расчетам, индикаторы деятельности здравоохранения, включая индикаторы ресурсов, результатов и эффективности, демонстрируют положительную пространственную автокорреляцию, что подтверждает гипотезу о наличии межрегиональных перетоков.