Оценка эффективности статического анализа для поиска дефектов естественной семантики программных объектов

тического анализа (СА), которые автоматизированно, а в некоторых случаях автоматически, на основе различных представлений программного кода обнаруживают дефекты и указывают их точную локализацию, обеспечивая полное покрытие исходного кода проверками. Применение программного кода в качестве входных данных анализатора дает возможность использовать СА на ранних стадиях разработки ПО, что в целом позволяет получить выигрыш в снижении затрат на его создание [1, 3]. Применение СА только для поиска нефункциональных дефектов ПО ограничивает эффективность данной методологии и не дает минимизировать суммарные затраты на разработку. Исследование возможностей СА для поиска функциональных дефектов (ФД) является актуальной научной задачей.

Для автоматизации процесса обнаружения некоторых ФД предлагается подход, основанный на СА исходного кода программ, оперирующих данными с ясным физическим смыслом (ускорение, скорость, длина, плоский угол и т.д.), и заключающийся в контроле выполнения принципа размерной однородности уравнений, нарушение которого предлагается называть дефектом естественной семантики (ДЕС). Естественная семантика – понятие, введенное для обозначения неизменных признаков программных объектов (переменных, функций и т.п.), отличных от семантики, определяемой требованиями спецификации языка программирования. В частности, в данной работе под естественной семантикой понимается размерность физической величины, интерпретируемая в объекте программы. Размерность величин, отталкиваясь от операций со степенями сомножителей формулы размерности физической величины, формализуется в виде вектора естественной семантики (ВЕС) некоторого линейного пространства с определенными операциями поэлементного сложения и умножения на скаляр [4].

Возможность использования вышеописанного подхода к обнаружению ФД должна быть исследована на предмет определения влияющих на него факторов и подкреплена оценкой его эффективности - комплексного свойства, отражающего качество получаемых результатов анализа. Показателями эффективности СА являются:

полнота (П СА ) – доля истинных среди существующих дефектов;

точность (ТСА) – доля истинных среди обнаруженных дефектов [5].

Полнота и точность СА для поиска ДЕС, исходя из соотношения множеств существующих и обнаруженных дефектов, может быть оценена до программной реализации алгоритма и представлена в терминах теории вероятностей. Ввиду того, что исследуемый подход не дает ложных срабатываний при анализе, но обладает другим недостатком - условно истинным обнаружением ряда вариантов искажений, предлагается вероятность обнаружения представлять суммой вероятностей истинного и условно истинного срабатывания анализатора. Тогда выражения для показателей эффективности будут иметь вид

D ИСТ _ | D ист|

D СУЩ   I D ОБН | + ^D ПРОП

р

ИСТ

— р + р

¹ ОБН ⁺ ‘ ПРОП

Р

ИСТ р + Р + Р

1 ИСТ + 1 УСЛ + 1 ПРОП

X = | D ИСТ | _ ^Р ИСТ _     ^Р ИСТ

| DОБН |   РОБН   PHCT + РУСЛ где DСУщ = DОБН U DПРОП - множество существующих дефектов; DОБН - множество обнаруженных дефектов; DПРОП - множество пропущенных дефектов; DИСТ - множество истинных дефектов; PОБН – вероятность обнаружения дефектов; PИСТ – вероятность истинного обнаружения дефектов; PУСЛ – вероятность условно истинного обнаружения дефектов; PПРОП – вероятность пропуска дефектов при анализе.

Расчет показателей полноты и точности СА для поиска ДЕС выполняется на графовых моделях, описывающих состояния анализатора в терминальных вершинах графа и варианты локализации дефектов в конструкциях вида: а К b , где а и b - операнды, представленные программными объектами; ⊗ – бинарная операция (арифметическая, присваивания, сравнения). Предполагается, что в рассматриваемой конструкции имеется только одно искажение в любой из составляющих. Моделирование производится при условии возможности искажения как операндов ( а ^ def, b ^ def) , имеющих ненулевые ВЕС ( ns ( а ) 4 0, ns ( b ) 4 0), так и операций ^{( К} > def ) с одинаковой вероятностью P ДЕФ , и допускает следующие состоя ния анализатора:

истинное срабатывание – указание на наличие ДЕС (на рис. 1, 3, 5 вершины серого цвета с непрерывным контуром);

условно истинное срабатывание – указание на наличие ДЕС при определенном сочетании составляющих конструкции программного кода (на рис. 1, 3, 5 вершины с прерывистым контуром);

пропуск – отсутствие сигнала при наличии ДЕС (на рис. 1, 3, 5 вершины белого цвета с непрерывным жирным контуром);

норма – отсутствие сигнала при отсутствии ДЕС (на рис. 1, 3, 5 вершины белого цвета с непрерывным контуром).

Логика определения состояния анализатора в терминальных вершинах графа модели ДЕС рассматриваемой конструкции а К b строится на утверждении об априорной известности результирующего ВЕС ns ( rec ) для выражения преобразования естественной семантики: ns ( а ) К ns ( b ), где ns ( а ) и ns ( b ) - ВЕС операндов программных объектов; Ф = {+, -, =} - операция с ВЕС. Состояния анализатора в терминальной вершине устанавливаются исходя из условия ns ( rec ) = ns ( а ) К ns ( b ) и варианта локализации ДЕС в исходной конструкции а К b , зависящего от возможности совпадения ВЕС истинного и искажающего программных объектов, а также от типа операции с программными объектами (арифметическая, присваивания и сравнения).

Для задания условия корректности моделей используется свойство, согласно которому сумма вероятностей несовместных событий, образующих полную группу: дефект существует, который может быть либо обнаружен ( P _ОБН = P ИСТ + P _УСЛ), либо пропущен ( P _ПРОП), и дефект отсутствует ( P ОТСУТ ) – должна равняться единице:

^P ИСТ ^{+ P} УСЛ ^{+ P} ПРОП ^{+ P} ОТСТ = 1. ⁽³⁾

Цель данной работы – разработка и использование для оценки эффективности СА графовых моделей ДЕС программных объектов для операций, которым возможно задать условие корректности согласно принципу размерной однородности физических уравнений.

Граф модели ДЕС для конструкций с арифметическими операциями {+, -, %, *, /} представлен на рис. 1. Пусть вершина a , соответствующая левому операнду бинарной операции, является начальной, из которой с вероятностью P _ДЕФ возможен переход в вершину a ^ def, отражающую ситуацию искажения операнда a . Распознавание искажения операнда возможно в случае изменения его ВЕС ns ( a ) 4- ns ( def) • Ситуация, когда дефект операнда существует, но его семантика осталась неизменной ns ( a ) = ns ( def) , происходит с вероятностью P _СВ и не обнаруживается. Вероятность P _СВ определяется диапазоном возможных значений естественной семантики программных объектов, т.е. чем больше объектов одной физической размерности в исходном коде программы, тем выше вероятность их появления в качестве искажающего воздействия.

Альтернативой ситуации наличия искажения левого операнда a → def служит событие в вершине a → a , иллюстрирующее отсутствие дефекта в a и происходящее с вероятностью 1 – P _ДЕФ. Событие искажения правого операнда соответствует вершине b → def , происходит с вероятностью P ДЕФ и является аналогичным искажению левого операнда.

Вершина ® соответствует ситуации возможного дефекта операции, которая исключает дефекты операндов и проявляется с вероятностью 1 - PДЕФ. Возникновение конкретной арифметической операции происходит с вероятностью Pi, каждая из которых может быть искажена с оди-i наковой вероятностью Pj, показывающей изменение i-й операции наj-ю, где i, j е {+, -, %, *, /}. Отсутствие дефекта операции проявляется с вероятностью Pi.

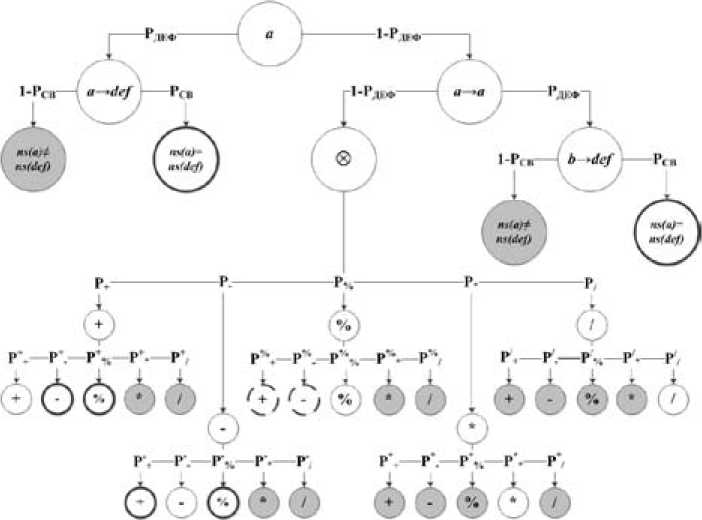
Рис. 1. Граф модели ДЕС программных объектов в арифметических конструкциях

Fig. 1. Model graph of software objects NSD for arithmetic construction

Ситуации искажения арифметических операций {+,-}, не изменяющих ВЕС программных объектов при преобразовании ( Р - , Р „% , Р „% , Р - ), не распознаются, так как ns ( res ) = ns ( a ) = ns ( b ). В случае замены операциями {+,-} исходной операции {%}, корректность преобразования естественной семантики которой контролируется по условию ns ( res ) = ns ( a ), возможны варианты появления условно истинных срабатываний анализатора при ns ( a ) = ns ( b ).

Вероятность существования и отсутствия дефекта арифметической операции в конструкциях программного кода при условии равной вероятности их искажения и равенства вероятностей искажения операций и операндов имеет вид:

Р _ДЕф = 4 P i , P i = const , i * j , ДЕФ j , j            ,        ,

1 — Р ДЕФ = P i , V i e { + , -%,*,/ } .

Вероятности истинного и условно истинного обнаружения дефектов в арифметических конструкциях, а также вероятность пропуска дефекта на основе графа модели ДЕС и соотношения (4) равны:

P" = ^{Р деф} [^{( 1 -} Р СВ ) ( ² - ^р двФ ) ⁺ 2 ( 1 ^{- Р}Д* ) ( 1 ⁺ P * ⁺ P ) ) , <«>

А

УСЛ

= 1 P Р деф ( 1 - Р деф ) 2 , 2

А

ПРОП

= Р деф ( ^ св + ( 1 — Р деф ) Р св + | ( 1 — Р деф ) 2 ( P ₊+      .

V                      ²                     V

Вероятность отсутствия дефекта в арифметической конструкции, исходя из соотношений (4) и (5), представляет собой

Р _ОАТСУТ = (1 - Р деф )²( P + P + + P - P + P % P % + P P * + P P^ = (1 - Р д_Еф ) 3 .        (9)

Корректность модели ДЕС программных объектов для арифметических конструкций подтверждается путем подстановки в соотношение (3) выражений (6), (7), (8) и (6).

Исходя из (1), (2), (3), (7) и (8), выражения для полноты и точности СА для поиска ДЕС в арифметических конструкциях следующие:

П

А

СА

( 1 — Р=, > ( ² - ^{р дЕ}Ф ) + 2 ( 1 - P Ф > о + P * + P ) ^Pk. - ^{3 Р} ДЕФ + ³

_{Т С}А_А

( 1 ^{- Р} СВ ) ( ^{2 - Р дЕф} ) + ¹ ( 1 ^{- Р дЕф} Г ( 1 ^{+ P +} P )   .

( 1 - Р СВ ^{) ( 2} - ^{Р дЕ}Ф ^{) +} 2 ^{( 1} - ^{Р дЕ}Ф ) ^{( 1} + ^Р- + ^Р + ^р % )

Зависимость полноты и точности СА для поиска ДЕС в арифметических конструкциях от вероятности наличия дефекта операнда или операции при фиксированных значениях вероятности совпадения ВЕС и вероятностей появления операций {*,/} и {%} в коде представлена на рис. 2.

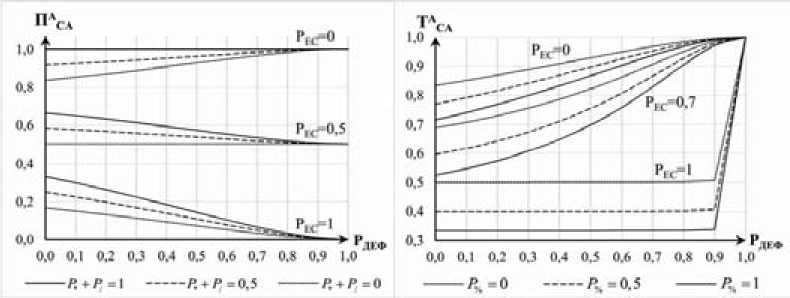
а)                                                             б)

Рис. 2. Графики зависимости полноты (а) и точности (б) СА для поиска ДЕС в арифметических конструкциях от вероятности наличия дефекта операции или операнда

Fig. 2. Schedules of dependence SA completeness (a) and accuracy (б) for searching NSD in arithmetic construction from probability of operation or operand defect existence

Полнота анализа арифметических конструкций возрастает при росте доли операций {*,/} в программном коде, для которых обнаруживаются все возможные варианты искажений. Точность анализа увеличивается при снижении доли операций {%}, так как для них существует возможность условно истинного срабатывания анализатора. Кроме того, сужение диапазона возможных ВЕС программных объектов, т.е. увеличение вероятности их совпадения, ведет к уменьшению показателей эффективности СА.

Для конструкций присваивания {=, +=, –=, %=, *=, /=} графовая модель ДЕС программных объектов изображена на рис. 3. Данная модель характеризуется наличием операций, которые с точки зрения принципа размерной однородности и принятых допущений моделей ДЕС являются некорректными {*=, /=}, так как при ненулевом ВЕС второго операнда в данных конструкциях будет наблюдаться дефект: ns ( res ) = ns ( a ) 4 ns ( a ) ± ns ( b ), ns ( b ) 4 0. Значит, вероятность наличия дефекта для операций {*=, /=} следующая:

РДЕф = 6 Pj = 1, Pj= const, Vi e{* =,/ =}.(12)

Вероятности существования и отсутствия дефекта операций {=, +=, -=, %=}, исключая заведомо неправильные конструкции с операциями {*=, /=}, при допущении о равенстве вероятностей дефекта операнда и операции представляет собой:

Рдеф = 5Р , Pj = const, i ^ j,(13)

1 -Рдеф = Р, Vi е{=, + =,-=,% =}.(14)

Анализатор пропускает взаимное искажение операций {=, +=, -=, %=} ввиду невозможности выявить несоответствие априорно известного результирующего ВЕС и результата – 12 –

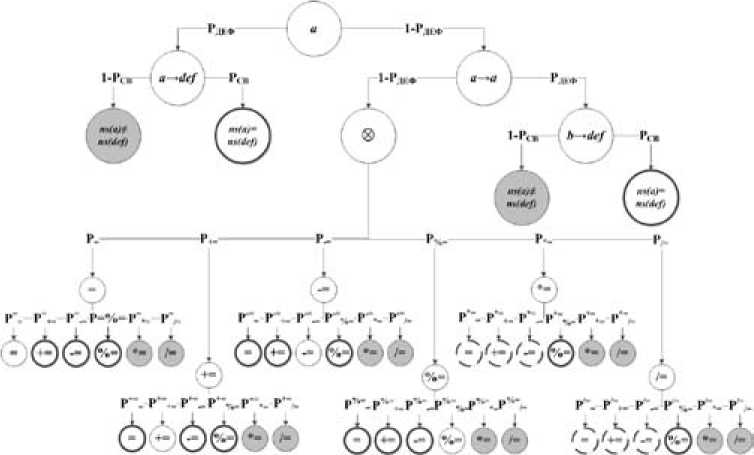
Рис. 3. Граф модели ДЕС программных объектов в конструкциях присваивания

Fig. 3. Model graph of software objects NSD for assignment construction

преобразования ВЕС операндов для операций, имеющих одинаковое условие корректности ns ( res ) = ns ( a ) = ns ( b ).

Состояние условно истинного срабатывания анализатора достигается для операций {*=, /=} при замене их на {=, +=, –=} вследствие неоднозначности результата проверки условия корректности для искажающих операций ns ( res ) = ns ( a ) = ns(b ). Ситуация наблюдается при совпадении ВЕС операндов ns (a ) = ns ( b ).

Исходя из соотношения (13), состояния истинного и условно истинного срабатывания анализатора, а также пропуск дефекта для конструкций присваивания происходят со следующими вероятностями:

П2

ИСТ ДЕФ (     СВ )(^ J ДЕФ) + ( ДЕФ) А х[2 РдЕ. ( Р . Р    Р_ + Р .1РД*. ( Р . Р.)),

Р УСЛ = 2 Р ДЕф ( 1 - Р ДЕФ )’ ( Р = + Р = ) .

Т ПРОП = ^Р ДЕФ Р СВ ^{( 2} — ^Р ДЕФ ) ^{+ ( 1} — ^Р ДЕФ ) ^х х| ³ Р дв ^ф( P + P₊ + P + P ) + ¹ P 1Е^ф ( P + P ) | . 1 5 ^Д "          -"     %"’ 6 ^Д "       ’)

Вероятность отсутствия дефекта в конструкции присваивания, основываясь на выражениях (12), (13), (14), имеет вид

роП   =(1 -P  )2(pp =+PP+=+pp-=+P p%=) =

ОТСУТ        ^ДЕФ = =    += +=     = =      % = % =

= ( 1 - ^Р Д^ЕФ ) ( ^P =^{+ P} +=^{+ P -}= ^{+ P} % = ) .

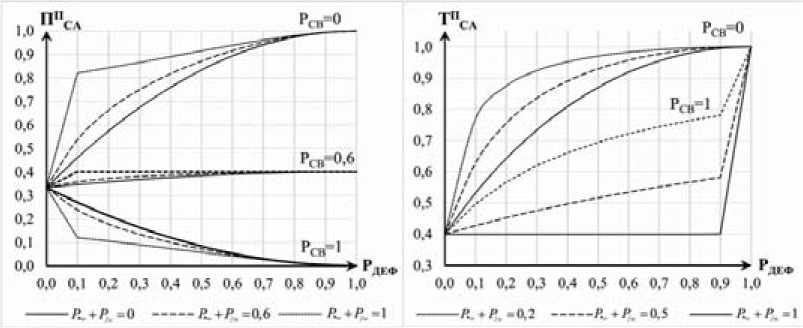
а)                                                             б)

Рис. 4. Графики зависимости полноты (а) и точности (б) СА для поиска ДЕС в конструкциях присваивания от вероятности наличия дефекта операции или операнда

Fig. 4. Schedules of dependence SA completeness (a) and accuracy (б) for searching NSD in assignment construction from probability of operation or operand defect existence

Исходя из (1), (2), (15), (16) и (17), выражения для полноты и точности СА для поиска ДЕС в конструкциях присваивания следующие:

П

П

СА

2 f 2                         1

РДЕФ (1- РСВ)(2 - рДЕФ) + (1- РдЕФЦ 5 РдЕФ + (P   P.) [ з

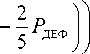
РдЕФ (2 РдЕФ) + (1 РдЕФ) (РдЕФ +(P*=+ P/=)(1 РдЕФ))

/                              /                X \

2

П

^Т СА

Р ДЕФ ( 1 — Р СВ ) ( 2 — Р ДЕФ ) + ( 1 — Р ДЕФ ) к Р ДЕФ + ( ^Р= + Р - ) к — Т Р дЕФ I I

77TV . (20)

Р (Х-Р Ш-р VU-P )² f2Р   р₊рх 5-2Р ))

ДЕФ (      СВ ) (^ ¹ ДЕФ ) ⁺ ( ДЕФ ) I г ¹ ДЕФ ⁺ ( *= + / = ) I       с ДЕФ I I

75             765   ))

С использованием выражений (19) и (20) получена зависимость полноты и точности СА для поиска ДЕС в конструкциях присваивания от вероятности наличия дефекта операнда или операции при фиксированных значениях вероятности совпадения ВЕС и вероятностей появления операций {*=, /=} в коде (рис. 4).

Полнота СА конструкций присваивания растет при уменьшении вероятности совпадения ВЕС. До уровня PCB ≈ 0,675 полнота анализа убывает при уменьшении вероятности появления в коде операций {*=, /=}, после данного значения зависимость принимает обратный характер. Точность СА конструкций присваивания зависит от частоты появления операций {*=, /=} и , увеличивается при снижении их доли в коде программы.

Операции сравнения {<, >, <=, >=, ==, !=} применяются только к операндам, обладающим одинаковыми ВЕС (рис. 5), откуда следует условие корректности для данных конструкций – 14 –

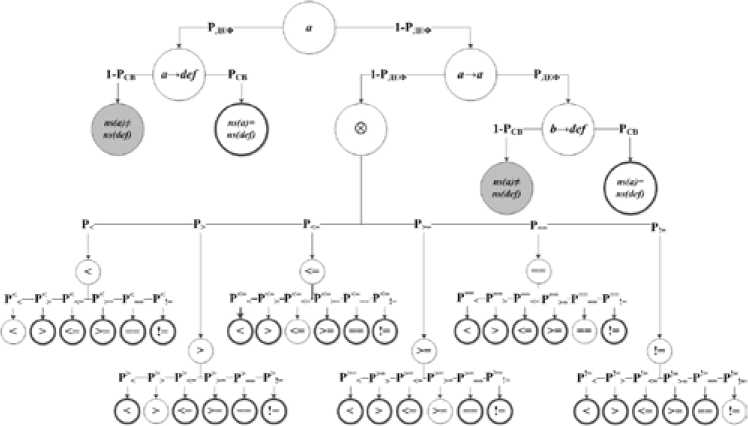
Рис. 5. Граф модели ДЕС программных объектов в конструкциях сравнения

Fig. 5. Model graph of software objects NSD for comparison construction

ns ( a ) = ns ( b ). Результатом выполнения операций сравнения является значение истина или ложь, что не позволяет определить наличие дефекта самой операции. Эффективность анализа конструкций сравнения зависит только от вероятности совпадения ВЕС операндов при искажении ( P св ) и не зависит от представленного в коде диапазона операций сравнения.

Условно истинных срабатываний анализатора при поиске дефектов в конструкциях сравнения не возникает ( Р _У ^С _СЛ =0), поэтому точность СА согласно соотношению (2) следующая:

С

Т СА ¹

.

События наличия и отсутствия дефекта операции сравнения, а также ее операндов проявляются со следующими вероятностями:

Р деф = 5 Р , Р = const , i * j ,

1 - Р деф = P i , V i е { < , > , <= , >= , == ,! = } .                                    (23)

Аналогично рассуждениям для вышеописанных моделей ДЕС программных объектов и на основании соотношений (22) и (23) для конструкций сравнения имеем:

С

^Р ИСТ P ДЕФ (^ P ДЕФ ) ( ^Р СВ ) ,

Р УСЛ = о,

P COn = ^Р ДЕФ ( Р СВ + ^{( 1} — ^РДЕФ ) Р СВ + ( ¹ — ^РДЕФ ) ) , P^0TcyT = ^{( 1} — ^Р ДЕФ ) .

Модель ДЕС программных объектов для операций сравнения корректна по соотношению (3) для полученных выражений (24), (25), (26), (27).

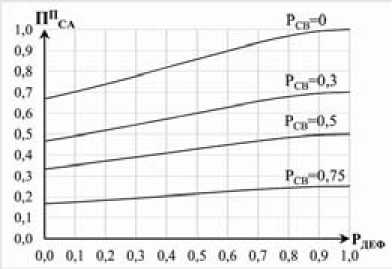
Рис. 6. Графики зависимости полноты СА для поиска ДЕС в конструкциях сравнения от вероятности наличия дефекта операции или операнда

Fig. 6. Schedules of dependence SA completeness for searching NSD in comparison construction from probability of operation or operand defect existence

Полнота СА для поиска ДЕС в конструкциях сравнения, исходя из соотношений (1), (24), (25), (26) такова:

С = ( 1 Р СВ ) ( ^{2 Р} ДЕФ )

СА      2

ДЕФ ДЕФ +

Согласно выражению (28) получена зависимость полноты анализа конструкций сравнения для поиска ДЕС от вероятности наличия дефекта операнда или операции при фиксированных значениях вероятности совпадения ВЕС (рис. 6).

Из анализа зависимости (рис. 6) следует, что полнота СА конструкций присваивания при уменьшении вероятности совпадения ВЕС повышается.

Таким образом, проведенное исследование позволяет сделать вывод о возможности применения СА для поиска нового типа функциональных дефектов – ДЕС программных объектов. Расчеты показали, что для ПО АС ВН, программные объекты которых интерпретируют широкий диапазон возможных значений естественной семантики, разрабатываемый подход является высокоэффективным. Данный факт открывает новые возможности по снижению затрат на верификацию ПО АС ВН.

• [1]    Ицыксон В.М., Моисеев М.Ю., Цесько В.А., Захаров А.В., Ахин М.Х. Алгоритм интервального анализа для обнаружения дефектов в исходном коде программ. Информационно-управляющие системы , 2009, 2, 34-41 [Itsykson V.M., Moiseev M.Ju., Tsesko V.A., Zakharov A.V., Akhin M.H. Interval analysis algorithm for detecting defects in the software source code. Informationcontrol systems , 2009, 2, 34-41 (in Russian)]

• [2]    Липаев В.В. Технико-экономическое обоснование проектов сложных программных средств. М.: СИНТЕГ, 2004. 284 с. [Lipaev V.V. Feasibility study of complex software projects. Moscow, SINTEG, 2004, 284 p. (in Russian)]

• [3]    Кулямин В.В. Методы верификации программного обеспечения. М.: Институт системного программирования РАН, 2008. 117 с. [Kuljamin V.V. Methods of software verification . Moscow, Institut sistemnogo programmirovanija RAN, 2008, 117 p. (in Russian)]

• [4]    Жидков Р.Е. Методика верификации программного обеспечения автоматизированных систем военного назначения по семантической модели. Сборник статей XXVIII Всероссийской научно-технической конференции школы-семинара «Передача, прием, обработка и отображение информации о быстропротекающих процессах» , М.: ИД «Академия Жуковского», 2017, 189-196 [Zhidkov R.E. Military automated system software verification technique by semantic model. Digest of articles XXVIII All-Russian Scientific Technical Conference school-seminar “Transmission, reception, processing and display of information on fast processes” , 2017, 189-196 (in Russian)]

• [5]    Глухих М.И., Ицыксон В.М., Цесько В.А. Использование зависимостей для повышения точности статического анализа программ. Моделирование и анализ информационных систем , 2011, 4(1), 68-79 [Glukhikh M.I., Itsykson V.M., Tsesko V.A. The use of dependencies for improving the precision of program static analysis. Modeling and analysis of information systems , 2011, 4(1), 68-79 (in Russian)]