Оценка эффективности влияния трубчатого турбулентного аппарата на кинетику процессов получения полимеров

В условиях модернизации существующих циклов непрерывного производства ведутся активные исследования, позволяющие изменить активность применяемых катализаторов и оказать значимое влияние на свойства получаемой продукции. Ключевой особенностью микрогетерогенных каталитических систем является получение продукта с достаточно высоким значением полидисперсности, что является следствием наличия в системе различных типов активных центров, способных проявлять различную реакционноспособность и стереоспецифичность[1]. С целью воздействия на кинетическую неоднородность применяются различные подходы, к которым можно отнести как изменение химического состава катализатора [2], так и изменение гидродинамического режима [3] в зоне реакции.

Проведенные экспериментальные исследования [4; 5] демонстрируют огромный эффект, который возникает после гидродинамического воздействия с использованием трубчатого турбулентного аппарата на состав, активность катализатора и, как следствие, на кинетику процессов получения полимеров.

В условиях действующего промышленного производства оценить эффективность гидродинамического воздействия на физико-химические свойства конечного продукта практически невозможно, что определяет актуальность модельного подхода к математическому описанию процесса, позволяющего воспроизвести необходимые сценарии ведения производства.

Целью данной работы является создание необходимых цифровых инструментов, позволяющих оценить эффективность использования трубчатого турбулентного аппарата на кинетику процессов получения полимерной продукции.

Обзор литературы

Вследствие микрогетерогенности используемых катализаторов изменение их дисперсного состава способно оказывать значимое влияние на свойства производимого полимерного продукта. В работе С. А. Будера1 впервые было показано, что при увеличении интенсивности перемешиваний реакционной смеси для процесса стереоспецифической полимеризации изопрена наряду с ростом скорости процесса наблюдается заметное снижение расхода катализатора.

Впервые конструкция такого трубчатого турбулентного аппарата (ТТА) была предложена А. А. Берлином2. Проводимые дальнейшие исследования [6]3 определяли возникающий эффект при интенсивном перемешивании. В своих научных обоснованиях исследователи руководствовались идеей разделения всех характерных для сложного процесса реакций на быстрые и медленные стадии, протекающие в различных потоках. Для формирования и последующего инициирования активных центров свойственна достаточно высокая скорость, что является причиной возникающих диффузионных ограничений и предопределяет неоднородность распределения образующихся активных центров [7-10]. Изменение гидродинамического режима с использованием ТТА позволяет отделить быстрые стадии и обеспечить практически идеальные условия протекания процесса.

В ранее проведенных исследованиях достаточно подробно изучались вопросы влияния турбулентного перемешивания на размеры частиц каталитической системы [11], а также на кинетические параметры, характеризующие скорости отдельных элементарных реакций [12].

Для оценки гидродинамического влияния исследователи руководствуются изменением числа активных центров, инициирующих процесс полимеризации. Изучение характера кинетической неоднородности катализатора проводится путем постановки и решения обратной задачи на основании первичной физико-химической информации в виде кривой молекулярно-массового распределения (ММР).

Классический подход, позволяющий оценить эффективность гидродинамического воздействия в турбулентных потоках на кинетическую неоднородность катализатора, предполагает решение задачи идентификации функции распределения активных центров ф ( X ) исходя из выражения:

X

q„ (м М» (а) к (^ м) d^ (1)

где λ – статистический параметра Френкеля; K ( X , M) - ядро интегрального уравнения, отражающее механизм полимери-зационного процесса; q _эксп( M ) - вектор, определяющий ММР продукта. В качестве ядра интегрального уравнения для микрогетерогенных каталитических систем чаще всего используется распределение Флори [13]

K ( X, M ) = Л² Me ~ ^{X M}. (2)

Задача вида (1) является некорректно поставленной и успешно решается с помощью метода регуляризации, предложенного академиком А. Н. Тихоновым⁴. Ранее данный подход успешно применялся для восстановления характера кинетической неоднородности каталитической системы на основе сольвата хлорида гадолиния [14; 15]. В частности, в работе В. П. Захарова и соавторов было описано исследование кинетической неоднородности титансодержащей и неодимсодержащей каталитических систем в условиях предварительного гидродинамического воздействия в турбулентных потоках, продемонстрировавшее снижение кинетической неоднородности [16]. Л. А. Бигаевой [17] с соавторами была решена обратная задача формирования молекулярно-массового распределения ионно-координационной полимеризации образца полиизопрена, синтезированного на каталитической системе TiCl₄– пиперилен-Al(i-C₄H₉)₃. В свою очередь А. С. Зиганшина [18] проводила исследование активности частиц каталитической системы TiCl 4 -Al(i-C 4 H₉)₃ путем изменения дисперсионного состава в процессе получения полибутадиена.

Во всех указанных случаях решения обратной задачи формирования молекулярно-массового распределения большое внимание уделяется параметру, характеризующему погрешность экспериментальных данных. Большая ошибка эксперимента приводит к «размыванию» хроматограмм, что отражается на получаемой кривой распределения активных центров и способствует неверной интерпретации результатов.

Материалы и методы

Программная реализация и вычислительные эксперименты, проведенные ранее, показали высокую чувствительность подхода к решению обратной задачи, основанного на методе регуляризации А. Н. Тихонова, к исходным экспериментальным данным. В работе [19] показано, что при погрешности лабораторных измерений более чем 10 % становится практически невозможно оценить доли активных центров, на которых образуются фракции полимеров с наиболее низкой молекулярной массой. Все это определяет необходимость учета влияния параметров погрешности на возможность корректного решения обратной задачи формирования молекулярно-массового распределения [20].

Кроме того, в ряде случаев часто возникали проблемы, связанные с высокой осцилляцией получающегося решения на концах, которые не позволяли качественно интерпретировать расчетные результаты. Часто успех решения обратной задачи зависел от корректности выбора параметра регуляризации α , единственным критерием для которого выступает минимизация функции невязки, определяющей абсолютную разность между экспериментальными и расчетными значениями распределения. При проведении вычислительных экспериментов нередко возникали ситуации, когда численные методы решения задачи в формуле (1) давали отличающиеся друг от друга результаты в виде совокупности параметров α и p_i , что определяло необходимость дополнительного анализа получающегося решения.

Проблемы возникают и в тех случаях, когда потенциальные активные центры 392

Том 33, № 3. 2023 расположены достаточно близко друг к другу. В частности, в работе [21] для полиизопрена на TiCl₄–ДФО–пиперилен– Al(i-C₄H₉)₃ авторы столкнулись с задачей разложения «размытых» максимумов, т. е. когда перекрывание отдельных функций существенно.

В условиях возникающих проблем была реализована альтернативная методика решения обратной задачи, позволяющая на основании единственного допущения о том, что распределение на каждом типе активных центров описывается одним из модельных распределений, в автоматическом режиме решить задачу подбора числа активных центров и долей каждого типа, а также кинетических параметров, способствующих образованию полимеров с заданной молекулярной массой на каждом активном центре.

Основная идея нового имитационного подхода заключается в том, что программным образом «разыгрываются» различные сценарии ведения процесса, определяемые числом активных центров – N , долей каждого активного центра в общем составе катализатора – p_i и кинетическими параметрами, которые определяют статистический параметр Френкеля – λ_i и приводят к формированию различных вариантов ММР. Воспроизводимое таким образом ММР, которое наилучшим образом описывает результаты эксперимента, в свою очередь определяет искомый набор параметров p_i и λ_i ( i = 1... N ). Таким образом, если классический подход к анализу кинетической неоднородности предполагает решение обратной задачи, то в условиях реализации новой методики проводится многократное решение прямой задачи воспроизведения вида ММР как суперпозиции распределений, характерных для каждого типа активного центра, и выбирается тот набор параметров p_i и λ_i , которые определяют ММР, максимально приближенное к экспериментальному.

Однако при всей логичности и структурированности предлагаемого подхода при его реализации потребовалось решить ряд возникающих проблем. Во-первых, неизвестно каким образом идентифицировать точное число активных центров, инициирующих процесс полимеризации. Действительно, если исходное ММР может быть описано наличием лишь N типов активных центров, то оно также легко может быть описано с помощью N +1 активных центров. В связи с этим в рамках реализации данного подхода к решению обратной задачи необходимо руководствоваться критерием минимизации возможного количества активных центров. Следовательно, на начальном этапе закладывается лишь один тип активного центра и определяются возможные кинетические параметры, позволяющие приблизить ММР к экспериментальному. Если же разница между экспериментальным и расчетным ММР превышает допустимую погрешность, то число активных центров увеличивается до двух и определяются возможные кинетические параметры, соответствующие каждому типу. Алгоритм повторяется до тех пор, пока разница между экспериментальным и расчетным ММР не станет менее максимально допустимого размера ошибки.

Вторая проблема выражается в достаточно низкой скорости обработки огромного количества сценариев при проведении вычислительных экспериментов. Для того чтобы многократный перебор различных вариантов молекулярно-массового распределения стал осуществимым, алгоритм пошагового воспроизведения был оптимизирован: все расчетные зависимости выведены за пределы итерационного поиска, шаг сдвига функционально зависит от величины ошибки. Однако наибольшее влияние на скорость расчетов оказала интеграция технологий параллельного программирования и технологий облачных вычислений [22‒24], эффективность которых уже была ранее продемонстрирована при исследовании сложных физико-химических процессов [25‒28].

Результаты исследования

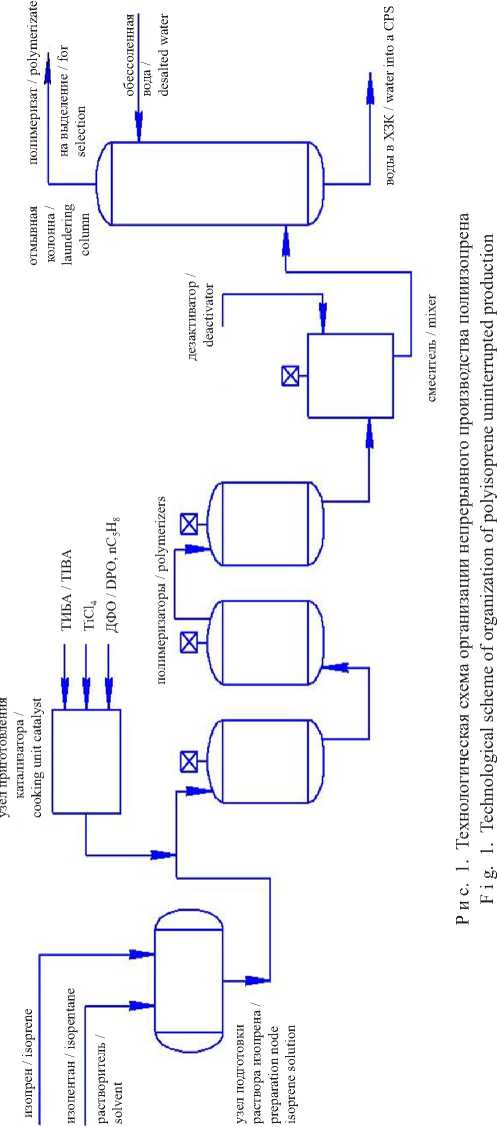
Апробация имитационного подхода к оценке кинетической неоднородности осуществлялась на промышленном производстве. Согласно технологическим условиям, непрерывный процесс получения полиизопрена организован в каскаде реакторов идеального перемешивания (рис. 1) объемом до 16,6 м3. Каждый реактор снабжен мешалкой, мощность электродвигателя которой составляет 30 кВт, что позволяет поддерживать постоянную скорость перемешивания (20÷40 оборотов в минуту). Поскольку организация какого-либо подвода теплоносителя отсутствует, то регулирование температуры ведения процесса осуществляется только за счет температуры поступающей реакционной смеси. Раствор мономера, который поступает в основную линию промышленного производства, формируется в результате смешения изопрена и возвратного растворителя.

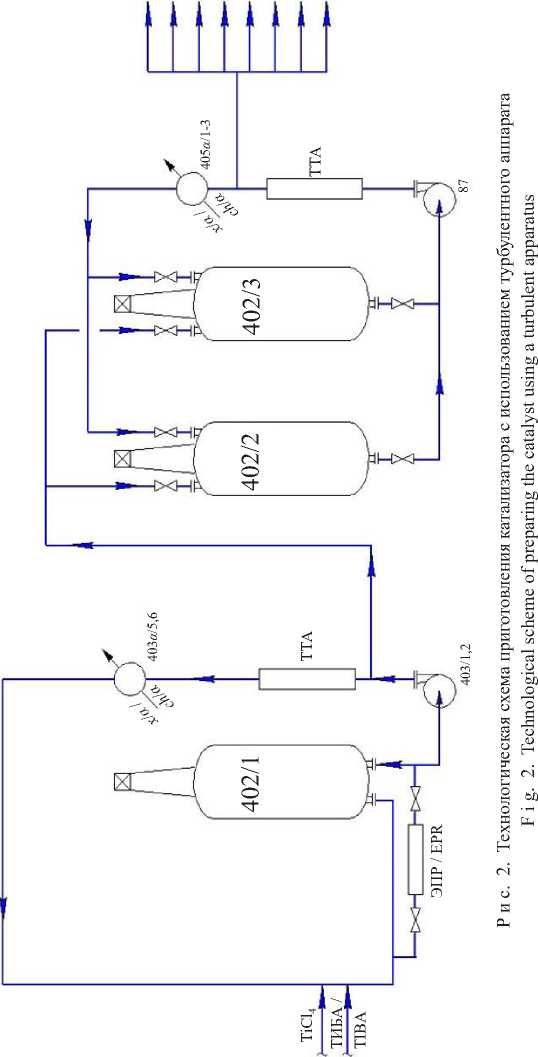
С целью воздействия на поверхностную структуру катализатора на стадии его приготовления установлен малогабаритный ТТА (рис. 2), оказывающий существенное влияние на характер кинетической неоднородности катализатора.

Непрерывный процесс получения полиизопрена в присутствии титанового катализатора предполагает использование всего двух реакторов каскада, а суспензию каталитического комплекса при этом получают при -10 ºC путем сливания толуольных растворов TiCl 4 (катализатор) с Al( i - C 4 H 9 ) 3 (со-катализатор), p-электродонорной добавкой дифенилоксида (ДФО) и -электродонорной добавкой пиперилена.

В полимеризаторе 8 батарей / In polymerizers 8 batteries

Состав катализатора формировали исходя из мольного соотношения TiCl4/ТИБА/ ПП/ДФО =1/1/0,2/0,15 c дозировкой 1 моль TiCl4/980 моль изопрена.

Полученный полиизопрен исследовался методом гель-проникающей хроматографии (ГПХ). Метод измерения основан на различии времен удерживания макромолекул полимера, растворенных в элюенте, в зависимости от их размеров в порах носителя разделяющей системы.

Апробация имитационного подхода проводилось последовательно. Согласно результатам эксперимента, индекс полидисперсности получаемого продукта составляет M w / M n = 2,56. Результаты проведенных расчетов для предполагаемых условий существования лишь одного типа активного центра представлены на рисунке 3. При этом было получено расчетное значение статистического параметра Френкеля λ = 1,6·10^-6. Для количественной оценки согласованности расчетного молекулярно-массового распределения с экспериментальным рассчитывалась величина ошибки

• 52 =L(qэксп [i]- qрасч [i])2,

  Том 33, № 3. 2023

которая составила 0,02. Очевидно, что если закладывать в систему организации расчетов лишь один тип активного центра, то он не способен будет обеспечить необходимую ширину молекулярно-массового распределения, а исходное молекулярно-массовое распределение нельзя описать моноцентровой моделью.

Продолжение работы алгоритма для случая использования двух типов активных центров позволило идентифицировать значения p = (0,91; 0,09) для λ = (1,5·10^-6; 8,7·10^-6). Величина ошибки δ² при этом составила 7,3·10^-4 (рис. 4). Дополнительных шагов для реализации имитационного подхода к решению обратной задачи не требуется, поскольку расчетное молекулярно-массовое распределение, получаемое в результате суперпозиции распределений, характерных для каждого типа активного центра, достаточно хорошо согласуется с итогами эксперимента.

В результате проведенных вычислений имитационный подход к решению обратной задачи формирования ММР позволил идентифицировать наличие двух активных центров: тип АTi - lnM = 13,4, тип ВTi - lnM = 11,7, при этом доля активных центров типа АTi составила 0,91; тип ВTi – 0,09.

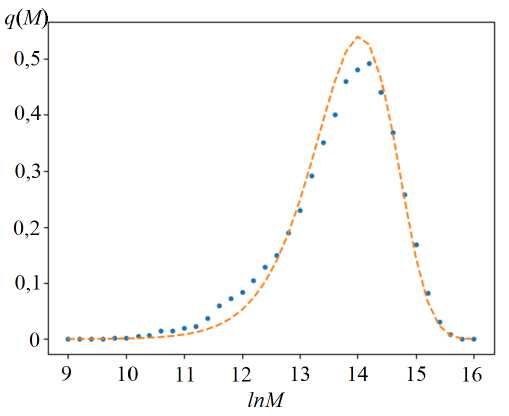
Р и с. 3. Результаты работы имитационного подхода к решению обратной задачи (точки – исходная кривая молекулярно-массового распределения; штрих – расчетная кривая)

F i g. 3. Results of the simulation approach to solving the inverse problem (dots are the initial curve of the molecular weight distribution; dashed line is the calculated curve)

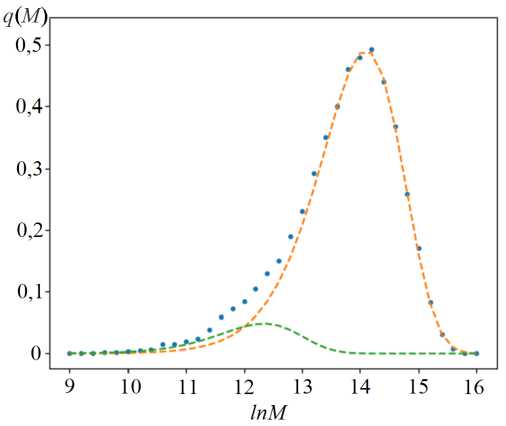
Р и с. 4. Результаты работы имитационного подхода к решению обратной задачи (точки – исходная кривая молекулярно-массового распределения; штрих – расчетная кривая для активных центров 1 и 2 типа)

F i g. 4. Results of the simulation approach to solving the inverse problem (dots are the initial curve of the molecular weight distribution; dashed line is the calculated curve for active centers of types 1 and 2)

Обсуждение и заключение

Таким образом, разработана методология решения обратных задач, которая позволяет на основании известной физико-химической информации определять влияние внешних факторов на кинетическую активность и неоднородность активных центров. В частности, на основании исходной кривой молекулярно-массового распределения представленный имитационный подход позволил оценить эффективность гидродинамического воздействия в турбулентных потоках на исходный состав катализатора в непрерывном производстве 1,4-цис-полиизопрена. Поскольку гидродинамическое воздействие оказывает существенное влияние на характер кинетической неоднородности и способствует усреднению реакционной способности активных центров, то часто максимумы могут быть расположены

близко друг к другу и сложно поддаются однозначной идентификации. Использование имитационного подхода в этом случае становится оправданным.

Апробация нового имитационного подхода к решению обратной задачи позволила оценить эффективность влияния трубчатого турбулентного аппарата на кинетику процесса получения полиизопрена в присутствии титанового катализатора и идентифицировать наличие двух активных центров: тип АTi - lnM = 13,4, тип ВTi - lnM = 11,7, при этом доля активных центров типа АTi составляет 0,91; типа ВTi – 0,09.

На основании полученных данных становится возможным проводить постановку и решение обратных задач идентификации кинетических параметров с целью дальнейшего модельного описания системы.

Поступила 05.07.2023; одобрена после рецензирования 01.08.2023; принята к публикации 20.08.2023.

Об авторах:

Все авторы прочитали и одобрили окончательный вариант рукописи.

Submitted 05.07.2023; revised 01.08.2023; accepted 20.08.2023.