Оценка экономической целесообразности разработки газового месторождения
Автор: Скиба А.К., Скиба Н.К.
Журнал: Труды Московского физико-технического института @trudy-mipt
Рубрика: Информатика и управление
Статья в выпуске: 2 (50) т.13, 2021 года.
Бесплатный доступ
Описывается непрерывная агрегированная динамическая модель газового месторождения. Исследуются три стратегии разработки газового месторождения при различных эксплуатационных условиях. Ставится и решается задача оптимального управления на максимум дисконтированной прибыли. Доказывается, что найденное решение является единственным. Предлагается численный алгоритм его поиска. Определяется критерий экономической целесообразности разработки газового месторождения.Основным математическим аппаратом является принцип максимума Понтрягина в форме Эрроу.
Динамическая модель газового месторождения, задача оптимального управления со свободным правым концом, фиксированным временем и со смешанным ограничением, максимизация прибыли, экономическая целесообразность разработки газового месторождения
Короткий адрес: https://sciup.org/142231482
IDR: 142231482 | УДК: 519.86 | DOI: 10.53815/20726759_2021_13_2_135
Текст научной статьи Оценка экономической целесообразности разработки газового месторождения
Природный газ является ценным сырьем, используемым в различных отраслях промышленности. Спрос на. него велик. В естественных условиях он находится глубоко под землей в основном в виде отдельных скоплений (газовые залежи) при высоком давлении и температуре [1]. Извлечение газа, из недр земли осуществляется скважинами, которые стараются разместить равномерно по всей территории месторождения.
Производственная добыча, газа, и его подготовка. - это сложный и трудоемкий, финансово затратный процесс, растянутый во времени на несколько десятков лет. Поэтому необходимо всесторонне исследовать этот и другие динамические процессы, затрагивающие
различные степени изученности рассматриваемого объекта. В этой связи особый интерес представляют математические модели.
В отделе Математических методов регионального программирования ФИЦ ИУ РАН на протяжении многих лет велись работы по математическому моделированию разработки нефтяных и газовых месторождений [2-4]. Данные модели при различных их модификациях подвергались всестороннему анализу. На них ставились и решались интересные оптимизационные задачи. Кроме того, рассматриваемые в отделе динамические модели использовались для численных расчетов при решении многих практических задач.
Среди оптимизационных задач, поставленных и решенных, особый интерес представляют две задачи: задача максимизации накопленной добычи для группы газовых месторождений с ограничением на пропускную способность газопровода [5] и задача максимизации длины их общей «полки» [6]. Первая из приведенных задач имеет экономическое содержание как максимизация совокупного дохода для группы газовых месторождений. Можно поставить и другие оптимизационные задачи с экономическим содержанием. Это минимизация затрат и максимизация прибыли.
Настоящая статья посвящена полному решению задачи максимизации прибыли с учетом коэффициента дисконтирования для одного газового месторождения. Данные задачи принадлежат к классу задач оптимального управления со смешанными ограничениями. Основным математическим аппаратом, используемым при их решении, является принцип максимума Понтрягина в форме Эрроу [7]. Результатом решения задачи является определение критерия экономической целесообразности.
1. Принцип максимума Понтрягина в форме Эрроу
Во второй половине прошлого столетия была опубликована статья К. Эрроу [7], ставшего впоследствии лауреатом Нобелевской премии по экономике. В основе работы лежит принцип максимума Понтрягина [8]. К. Эрроу модифицирует принцип и формулирует предложения, которые позволяют решать задачи оптимального управления со смешанными ограничениями. В предложения дополнительно включены некоторые элементы нелинейного программирования такие, как Лагранжиан, множители Лагранжа и условия дополняющей нежесткости. Автор настоящей статьи использовал модифицированный принцип в своей работе [9].
Сформулируем предложения К. Эрроу.
Предложение 1. Пусть v(t) - управления (0 6 t 6 Т ), максимизирующие функционал
[ U[cc(t), v(t), t] dt при условии
-
( а ) Х = G[x(t), v(t), t],
ограничениях на управления
-
(b) F[x(t),v(t),t] > 0 ,
которые, возможно, включают переменные состояния, начальных условиях на переменные состояния и граничных условиях
х(Т ) > 0 .
Если условия регулярности выполнено, то существуют сопряженные переменные p(t) такие, что для каждого момента t
-
(с) v(t) максимизирует Н [x(t), v,p(t), t] относительно ограничений (b), где
Н (x,v,p,t) = U (x,v,t) + pG(x,x,t);
-
(d) p = -dL/dxi пр и x = x(t), v(t) = v(t), p = p(t), где
-
(е) L(x,v,p,q,t) = H (x,v,p,t') + qF (x,v,t)
и множители Лагранжа q такие, что
(f) dL/d^k = 0 при x = x(t), v(t) = x(t), p = p(t),
2. Построение модели и исследование некоторых стратегий освоения газового месторождения
q > 0, qF [x(t), v(t), t] = 0.
В предложении 1 вектор x(t) имеет размерность п, а вектор v(t) - размерность т. Перейдем к описанию модели и постановки задач.
Рассмотрим модель функционирования газового месторождения с взаимовлияющими скважинами [2-4]. Введем следующие обозначения:
t - время, будем считать, что мы наблюдаем за разработкой газового месторождения, начиная с момента t = 0:
q(t) - средний дебит добыва ющих скважин в момент t:
q° - начальный средний дебит добывающих скважин;
n(t) - количество скважин, вводимых в строй в едпшщу времени (следует отметить, что п - величина целочисленная, но для простоты исследования будем допускать для нее любые неотрицательные действительные значения, что можно сделать ввиду большого количества скважин, обычно бурящихся на месторождении);
nt) - максимальные возможности по вводу в строй новых скважин;
N (t) - общий фонд добывающих скважин в момент t:
N 0 - начальный фонд добывающих скважин;
N (t) - действующий фонд добыватощнх скважин в момент t:
N‘(t) - резервный фонд добыв;мощих скважин в момент t:
Q(t) - текущая добыча газа;
Q - пропуская способность трубопровода;
-
V(t) - извлекаемый запас газа, оставшийся в месторождении в момент t;
-
V 0 - начальный извлекаемый запас газа;
-
8 - коэффициент дисконтирования;
с - продажная цена природного газа;
к - стоимость строительства одной скважины.
Между описанными выше переменными устанавливается взаимосвязь, которую мы представляем в виде системы обыкновенных дифференциальных уравнений:
-
V = -Q(t) = -N (t)q(t),(1)
q0
-
q = — V0 q(t)N(t) = -«q(t)N(t),<
N = n(t)(3)
при ограничениях
0 < N(t) < TV(t),(4)
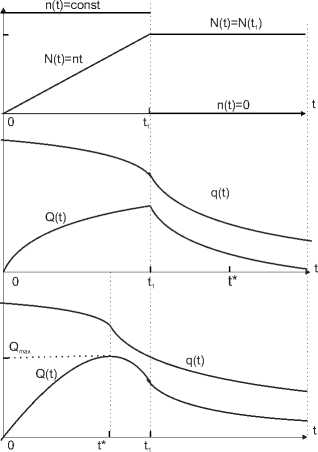
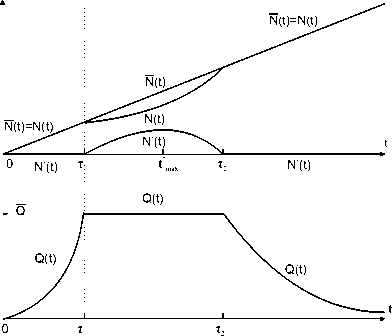
0 < n(t) с начальными условиями V0 > 0,(6) q0 > 0,(7) N0 > 0, Заметим, что параметр a = ф0 , используемый в написании дифференциального уравнения (2), предназначен только для упрощения вида математических выражений. Кроме того, в любой момент t общий фонд скважин равен сумме резервных и действующих фондов скважин, т.е. N (t) = N '(t) + N (t). Предполагаем, что в любой момент t месторождение покрыто равномерной сеткой скважин. Управление динамическим процессом разработки месторождения осуществляется за счет ввода новых скважин n(t) и величиной действующего фонда добывающих скважин N(t) Кроме того, будем считать, что бурение скважины и возможность её ввода в разработку месторождения происходят в один и тот же момент времени. Для иллюстрации возможностей модели рассмотрим три стратегии освоения одного газового месторождения. Стратегия 1. Предположим, что мы имеем одно месторождение с известным запасом газа V0 и один трубопровод с заданной его пропускной способностью Q. Необходимо нам в динамике определить величину действующего фонда сквасисин N(t), которое обеспечивало нам полное извлечение всего запаса газа при постоянном заранее заданном уровне его добычи Q. Интерес в постоянном уровне добычи газа проявляется как со стороны потребителей газа, так и со стороны промысловиков. Потребителям газа постоянный уровень добычи необходим при решении вопроса о стабильном объёме закупок газа. Промысловикам постоянный уровень добычи необходим для закупки и настройки промыслового и транспортного оборудования под обеспечение добычи газа требуемого уровня. Приведённые выше доводы делают интересными теоретическое исследование данной стратегии освоения газового месторождения. Перейдём к формальному описанию и исследованию упомянутого режима. Объем действующего фонда скважин описывается следующей формулой: N (t)= — Q q° — aQ t . (Ю) В последней формуле дебит скважины q(t) изменяетмя по линейному закону. Таким образом, мы определяем функция (10) на полуинтервале [0.t*), г де t* = ^О. Согласно рассматриваемой модели фазовая переменная N(t) удовлетворяет неравенству (4) и соотношению ^ N(0) = |0 < N0 в начальный момент. В конечный момент t* происходит полное извлечение запасов газа из месторождения. В то же время limt^t* N(t) = то. Следовательно, в этом случае сетка скважин должна быть уплотнена до бесконечности. Эту стратегию невозможно полностью реализовать на практике. Однако она может быть реализована частично. Этапу постоянной добычи газа предшествует этап нарастающей добычи, который для небольших газовых месторождений может и отсутствовать. За этапом постоянной добычи следует этап падающей добычи. Проблема увеличения периода постоянной добычи особо актуальна в настоящее время. Такая ситуация возникает, например, в случаях, когда неожиданно нарушаются объемы поставок с других газовых месторождений, и в соответствии с договором между поставщиком и потребителем газа необходимо оперативно компенсировать появившуюся недостачу. На рис. 1 схематично изображены в динамике два графика, относящиеся к добыче газа Q(t) и к действующему фонд у добывающих скважин N (t). Стратегия 2. Рассмотрим динамическое поведение описанной выше модели (1) - (8) на двух временных периодах разработки газового месторождения: на не нулевом первом периоде от 0 до t1 темп разбуривания месторомсдения постоянен, n(t) = п, и в дальнейшем при t > t1 бурение новых сквазісап прекращается, т.е. n(t) = 0. Предполагаем, что действующий фонд скважин совпадает с общим фондом при всех значениях t > 0 м N0 = 0. Рис. 1. Графики добычи газа Q(t) и действующего фонда добывающих скважин N(t) Мы получаем следующие основные динамические показатели: nt при t Е [0, ti] nti при t > ti; N(t) = { ( q° exp[—t2] при t G [0,ti] ( q(ti) exp[—N(ti)(t - ti)] при t > ti; v(t) = Г V0 exp[—TPt2] при t Е [0, ti] U ( V(ti)exp[-N(ti)(t - ti)] при t > ti; Q(t) = { q°nt exp[-TP t2] при t Е [0, ti] q(ti)N(ti) exp[—N(ti)(t — ti)] при t > ti. Исследование последней функции показвівает, что на началвном этапе бурения месторождения добыча газа Q(t) на нем возрастает. Данный факт объясняется следующим образом. Увеличение прироста добычи газа за счет ввода в эксплуатацию новых скважин n(t) превышает естественный темп снижения добычи. Если ti имеет небольшое значение, то в момент ti (в момент прекращения ввода новых скважин) добыча Q(t) достигает максимального значения. В этом случае на графике мы могли бы наблюдать характерный ярко выраженный излом. Далее добыча газа падает. Если ti имеет значительную величину, то прирост добычи газа за счёт ввода новых скважин будет со временем постепенно уменьшаться, и в момент Tnax (И) прирост совпадёт с естественным темпом падения добычи. В этот момент текущая добыча достигает своего максимального значения: Qmax ^ q0nV0 В дальнейшем добыча газа падает. Такие характерные особенности поведения добычи газа наблюдались на практике при бурении газовых месторождений. На рис. 2 схематично изображены в динамике основные показатели разработки газового месторождения: Рис. 2. Динамика основных показателей разработки газового месторождения: п(1) - количество скважин, вводимых в строй в единицу времени; N(1) - действующий фонд добывающих скважин; q(t) ~ средний дебит добывающих скважин в момент 1; Q(1) - текущая добыча газа • п(1) - количество скважин, вводимых в строй в единицу времени; • N(1) - действующий фонд добывающих скважин; • q(1) ~ средний дебит добывающих скважин в момент 1; • Q(1) ~ текущая добыча газа. Дебит скважины q(1) и добыча газа Q(1) дважды изображены на этом рисунке. Один раз это связано со случаем, когда прирост добывающих скважин прекращается на этапе возрастающей добычи Q(1). Другой раз - на этапе падающей добычи Q(1). На рис. 2 не изображена динамика извлекаемого запаса газа V(1). В этом нет особой необходимости, т.к. дебит скважины q(1) отличается от извлекаемого запаса газа V(1) на известную постоянную величину. Стратегия 3. Рассмотрим динамическое поведение модели (1) - (8) при 1 > 0. Делаем следующие предположения: • месторождение начинает разрабативатися при нулевом общем фонде скважин N0 = 0: • темп бурения скважтн на месторождении постоянен п(1) = п: • имеется ограничение сверху на пропускную способности трубопровода: _ / q°nV0 Q < Qmax — у ^ , где Qmax определяется из (16); • действующий фонд сквазісин равен оощему фонду скоаэісии при условии q(t)N(1) < Q. в противном случае q(1)N(1) — Q. Добыча газа состоит из трех последовательных этапов: этап возрастающей добычи, этап постоянной добычи и этап падающей добычи. На первом и последнем этапах N(1) — N(1). Рис. 3. Временные зависимости добычи газа Q(t), общего фонда добывающих скважин N(t), действующего фонда добывающих скважин N (t) и резервного фонда дсбывающих скважин N‘(t) На втором этапе согласно равенству (9) появляется ненулевой резервный фонд N‘(t) и N(t) Начало второго этапа ті находится из решения уравнения q°nte^n£2/2 = Q (14) на отрезке [0,tmax], г де tmax определяется из (11). С учетом (11) - (13) легко показать, что уравнение (14) имеет единственное решение на отрезке [0,tmax]. Учитывая (10) и линейную зависимость общего фонда скважин от времени, вычисляем время окончания второго этапа по следующей формуле: 1 Т2 = -----. апт1 Резервный фонд достигает своего максимального значения при t*max = ті + Т2 — фТ| т2. Оно равно величине п(Дт2 — Дту)2. На рис. 3 в динамике изображены добыча газа Q(t), общий фонд добывающих скважин N(t), действующий фонд добывающих скважин N(t) и резервный фонд добывающих скважин N‘(t). 3. Постановка и решение задачи на максимум прибыли Задача 1. О максимизации прибыли с учетом коэффициента дисконтирования для одного газового месторождения Для системы обыкновенных дифференциальных уравнений (1) - (3) с начальными условиями (6), (7) и NN0 = 0 (15) на фиксированном интервала времени [0,Т] требуется наити функции n(t) и N(t) удовлетворяющие ограничениям (4), (5) и соответствующую этим функциям траекторию (q(t),N(t)), которая доставляет максимальное значение функционалу I [cQ(t) — &n(t)j exp(—St) dt. Правый конец оптимальной траектории (g(t),N(t)) считается свободным. Функция n(t) в двойном неравенстве: (5) является постоянной величиной, равной значению п > 0. В этом случае двойное неравенство (5) представится в следующей форме: 0 < n(t) < п, п > 0. Заметим, что дифференциальные уравнения (1) и (2) взаимосвязаны, и фазовые переменные q(t) и V(t) имеют между собой линейную зависимость при любых допустимых управлениях, т.е. q(t) = aV(t) Поэтому в дальнейшем достаточно ограничиться только двумя фазовыми переменными q(t) и N(t) К управляющим параметрам относятся переменные n(t) II N(t) В описание прибыли (16) включен коэффициент дисконтирования 5, позволяющий соизмерять доходы и затраты, производимые в различные моменты времени. Сформулируем и докажем следующую теорему. Теорема 1. Оптимальные управления n(t) и N(t) в задаче максимизации прибили существуют и единственны. Управляющая переменная n(t) принимает один вид из двух возможных вариантов: / й n ри t € [0,т ], т € (0,Т) n(t) = t 0 nput Е (т,Т ]; n(t) = 0. (19) Другое оптимальное управление N(t) при всех значениях t Е [0, Т] принимает верхнюю границу неравенства (4), т.е. N(t) = N(t) Доказательство. Рассматриваемая задача 1 является задачей оптимального управления со свободным правым концом, фиксированным временем и со смешанным ограничением. Существование оптимального управления следует из теоремы, приведённой в монографии [10, § 4.2]. Доказательство единственности мы приведем в конце теоремы 1. При решении задачи 1 мы не можем применять принцип максимума Понтрягина [8, 11] в классической формулировке, поскольку в ее постановку включается смешанное ограничение (4). Для решения этой задачи мы используем принцип максимума Понтрягина в форме Эрроу [7]. Мы воспользуемся модифицированной формой представления гамильтониана Н, лагранжиана, L. сопряженных переменных ДД) ii p(t). множителей Лагранжа, 31,32,71 11 72. Такую же модифицированную форму использовал К. Эрроу в своей статье [7]. Согласно предложению 1, выпишем гамильтониан и лагранжиан: Н(q, N, n, Д Д) = cqN — kn — ^aqN + pn, (20) L(q,N,N,n,^,p, 31,32,71,72) = = cqN — kn — ^aqN + pn + 31(N — N) + 32N + 71 (n — n) + 72m Обращаем внимание, что в описании гамильтониана, (20) отсутствует в явном виде фазовая переменная N(t) однако она присутствует в описании лагранжиана. В каждый момент t Е [0, Т] управления N и n максимизируют гамильтониан: Н (q(t),N(t),n(t),^(t),P(ty) = max Н (q(t),N,n,3(t),p(ty). Nе[0,М; ne[G,n] Отсюда, и из (20) следует iv(t) = I ~ — N(t) при c > a3(t) при c< a^(t)]; n при p(t) > k при p(t) < k. Сопряженные уравнения представятся в виде ■ = бр — дь dq = бф — cN + ■aN; р = бР - dN = бР - 3ь Для множителей Лагранжа 31,32,71,72 справедливы следующие равенства: дЬ dN = cq—^as + 32— 3i = 0; дь — = р — k + 72 — 71 = 0; дп (24) 3i(7V — N) =0, 31 > 0; (25) 32N = 0, 32 > 0; (26) 71 (п — п) = 0, 71 > 0; (27) 72п = 0, 72 > 0. (28) Равенства (25) - (28) являются условиями дополняющей нежесткости. На правых концах сопряженных переменных ■ (t) и p(t) выполняются условия трансверсальности: ■(Т) = р(Т) = 0. Пусть в момент t Е [0, Т] выполняется неравенство c< аф(і), тогда из (21), (22) и положительности ■(t) следует дальнейшее возрастание сопряженной переменной ■(t). Условия трансверсальности (29) нарушаются. Значит, c > a^(t) и N(t) = N(t) при всех t Е [0, Т]. Из (26) вытекает 32 = 0. С учетом (24) перепишем уравнения (22) и (23): ф = бф — cN + ■aN; (30) р = бр — cq + ■aq. (31) Рассмотрим всевозможные сопряженные переменные ■ (t) и p(t). Среди функций ■ (t) и p(t) будем выделять сопряженные переменные, удовлетворяющие условиям трансверсальности (29). Утверждение 1. 1. Сопряэюенная переменная ■ (t), соответствующая оптимальной траектории, неотрицательна. 2. Пусть выполнено равенство ■(t) = 0 при некотором значении t Е [0,Т), тогда ■(t) = 0, n(t) = и справедливо следующее неравенство: ca° г , -^- [1 — exp(—6t)] < k. Доказательство. Из сопряженного уравнения (30) видно, что при отрицательных значениях переменной ■(t) условия трансверсальности (29) не выполняются. Переходим к рассмотрению второй части утверждения 1. Из предположения ■(t) = 0 при 0 < t < Т, условий трансверсальности (29) и сопряженного уравнения (30) вытекает, что ■ (t) = 0, n(t) = 0, N(t) = 0 не только на временном интервале [t, Т], но и на всем рассматриваемом периоде [0, Т]. Значит, месторождение не подвергается разработке и дебит скважины остается постоянным на всем рассматриваемом периодо [0, Т]. т.е. q(t) = q0. С учетом условий трансверсальности (29 проинтегрируем дифференциальное уравнение (32 (37) от 0 до Т при условиях: W(t) = 0 и q(t) = q° В результате мы получаем p(t) = ^{1 - exp[—5(Т — t)]}. (33) Из (33) видно, что p(t) убывающая функция. Поскольку оптимальное управление n(t) = 0 II при этом управлении достигается максимум гамильтониана. то p(0) < к. Отсюда и из соотношения (33) следует выполнение неравенства (32). Утверждение 1 доказано. Утверждение 2. Пусть (q(t),N(t)) является оптимальной траекторией при допол-нителъном условии NT) > 0, тогда на полуинтервале t Е [0.Т): 1. выполняется двойное неравенство 0 < ^(t) < ^ и ^(Т) = 0; 2. сопрямсенная переменная p(t поломсительна и строго убывает, и р(Т) = 0. Доказательство. Умножаем обе части сопряженного уравнения (30) на q и после несложных преобразований с учетом (2) получаем 4 W\ = SWq — cqN. (34) at Умножим обе части дифференциального уравнения (34) на exp(—St) и после несложных преобразований проинтегрируем обе части полученного равенства от t до Т. Учитывая условия трансверсальности (29), приходим к соотношению W(t)q(t) exp(—St) = с J о(Ө)1Ч(Ө) exp(—SӨ) дӨ. (36) В силу положительности q(t) и N(Т). непрерывности и пеотрптіателыюсти N(t) вытекает, что интеграл в правой части равенства (35) положителен. Отсюда положительна сопряженная переменная W(t) при t Е [0, Т) и ф(Т) = 0. Принимая во внимание (2), преобразуем (34). В результате получаем следующее дифференциальное уравнение: 4 [(W — -)qexP(-St)] = —qexP(-St). at a a С учетом условия трансверсальности (29) проинтегрируем обе части последнего соотношения от t по Т; [--W(t)l q(t) exp(-St) = —о(Т)exp(-ST) +I о(Ө) exp(—SӨ) дӨ. La J a a Jt Правая часть равенства (22) положительна. Значит, W(t) < д- Первая часть данного утверждения доказана. Переходим к доказательству последней части утверждения 2. С сопряженным уравнением (31) проделаем те же операции, что и с уравнением (30). После всех преобразований решение сопряженного уравнения (31) представится в виде интегрального выражения p(t) = exp[St] / [с — aW(Ө)]q(Ө) exp(-SӨ) дӨ. (36) Отсюда следует, что сопряженная переменная p(t) положительна на полуинтервале t Е [0.Т). Умножаем обе части сопряженного уравнения (30) на q, и после преобразований с учетом (2) получаем ^ [aWq — cq] = SaWq. Продифференцируем по t обе части сопряженного уравнения (31) и, подставив в полученное выражение последнее равенство, приходим к следующему дифференциальному уравнению второго порядка: p — Sp = SaWq. Умножаем обе части дифференциального уравнения на exp(—6t) и после преобразований с учетом (2), (29) и (31) проинтегрируем от t до Т полученный результат: p(t) = р(Т) exp[—5(Т — t)] — 5a J" 'ф(Ө)q(Ө) exp[—о(Ө — t)] dO = —cq(T) exp[—5(Т — t)] — 5a J ф(Ө)д(Ө) exp[—ДӨ — t)] dO. Отсюда следует, что сопряженная переменная p(t) строго убывает. Утверждение 2 доказано. Из утверждений 1 и 2 вытекает справедливость одного из соотношений (18) или (19). Переходим к доказательству единственности оптимальных управлений. Общая схема доказательства единственности состоит в следующем. Преобразовываем формулу (36) для определения сопряженной переменной p(t) и устанавливаем зависимость р(т). Доказываем строгую монотонность функции p(t) Следователь но, уравнение р(т) = к будет иметь на отрезке [0, Т] не более одного решения, что приводит нас к единственности оптимальных траекторий. Для упрощения вида формул при доказательстве единственности мы надчеркивание у переменных временно опускаем. Пусть решение задачи 1 описывается формулой (18). В этом случае с учетом (2), (3), (7) и (15) общий фонд добывающих скважин и дебит скважин изменяются следующим образом: V(t) = | nt при t Е [0, т], т Е (0, Т) пт при t Е (т,Т]; _(t) = Г q° exp[—ant2/2] при t Е [0, т], т Е (0, Т) q( q° exp[an(t2/2 — tт)] п put Е (т, Т ]. Представим в формуле (36) сопряженную переменную p(t) при т< t <Т в виде разности двух интегралов: p(t) = / cq(Ө) exp[—5(Ө — t)] dӨ — а / ^(Ө)q(Ө) exp[—5(Ө — t)] dӨ = 11 — 12. (39) С учетом (2), (3), (15) и (18) преобразуем интеграл 11; І1 = I cq(Ө) exp[—д(Ө — t)] dӨ = —q^ {1 — exp[—(апт + 5)(Т — t)]}. (40) Jt апт+о С учетом (37), (38) и т< t <Т преобразуем соотношение (35): ^(t)q(t) = cq(t)nт {1 — expHamr + 5)(Т —t)]}. апт + о Отсюда при т< t< Ө <Т получаем ф(Ө)q(Ө) exp[—5(Ө — t)] = cq^ т {1 — exp[—(апт + 5)(Т — t)]} exp[—(апт + 5)(Ө — t)]. апт + о Используя предыдущее соотношение, преобразуем интеграл І2 из (39): 12 = а J ф(Ө)q(Ө) exp[—д(Ө — t)] dӨ = = Cq(t)anT2{1 — exp[—(апт + 5)(Т — t)]} — С^(^а1. (Т — y)exp[—(апт+5)(Т — t)]. (апт + о ) апт + о С учетом (40) и последнего выражения для І2 перепишем функцию (39): , . cq(t) , г , _х cq("t^anт , г , _х Х1, ^(t) =----— {1 - ехр[-(апт + °)(Т - t)]} - -----{1 - ехр[-(апт + °)(Т - t)]}+ апт + о (апт + °)2 + 'q ' - exp[-(апт + °)(Т - t)]. апт + о В последнее выражение подставим (38) при t = т. В результате получаем ^(t) = cq0е-ап^/2{-----°—- [1 - е-(апт+5)(т-т)] + "7(т - т)е-(апт+8)(т-т)}. L (апт + °)2 апт + ° Продифференцируем функцию ^(т): ^'т —canтqoe ant2/2{°- е~(апт+<5)(Т-т) (апт + °)2 + апт(Т - т)е-(апт+5)(Т-т)} + апт + ° +cq0е-апt2/2{-(ап)2т(Т-(“^+5)(T Т) + апт(Т - т)е-(апт+8)(т-т)- -т[ап(Т - т)]2е-(аПт+<$)(т-т) +ап(Т -) - "'т:+5)(т-т) - аптс-(аПт+б)(т-т)-апт + ° апт + ° апт + ° 2°ап[1 - е-(апт+)(Т-т)] °е-(апт+^)(Т-т) °ап(Т - т)е-(апт+)(Т-т) (апт + °)3 апт + ° (апт + °)2 Докажем, что <^т < 0 ПРи т € [0,Т]. Все члены математического выражения разбиваем на три непересекающиеся группы. Каждую группу мы отделяем фигурными скобками с положительным множителем. Дополнительно мы вводим обозначения Ғ1, Ғ2 и Ғ3. ф'т = сапт q0е ant2/2{-° 1 е-(апт+5)(Т-т) (апт + °)2 апт (Т - т )е - (апт+8)(Т- т) апт + ° +(Т-т )е-(“пт+5)(Т-т)}+ +cq0е-апt2/2{ ап(Т - т)е-(“пт+5)(Т-т) апт + ° °ап(Т - т)е-(“пт+5)(Т-т) (апт + °)2 2°ап[1 - е-(апт+5)(Т-т)] (апт + °)3 (ап)2т(Т - т)е (“«т+^)(Т т) } + cq0е-ant2/2{-т[ап(Т - т)]2 (апт + °)2 апт + ° - 1}е-(“ит+5)(Т-т) = = cаптq0 е-“nt2/2F1 + cq0е-“nt2/2 F2 + cq0е-“nt2/2-(“nт+г)(T-т)Ғ3. Функция Ғ3 отрицательна, т.к. она содержит только отрицательные члены. Покажем, что (руикции Fi л Ғ2 отрицательны при т € [0, Т]. Действптелыю: = -° 1 е ( + )( ) - апт(Т т)е-(а«т+<5)(Т-т) + (т - т)е-(“"т+)(Т-т) = (апт + °)2 апт + ° хр — (апт+8)(Т—т) = - (апт + 1)2 +5)<Т-Г) - 1 - <“"т + ° " Т - т)]< 0 ғ _ ап(Т - т)е-(апт+5)(т-т) + °ап(Т - т)е-(апт+5)(т-т) 2°ап[1 - е-(апт+5)(т-т)] апт + ° (апт + °)2 (апт + °)3 (а-nA 2т(Т — -(апт+5)(т-т) 25ае-(апт+5)(т-т) , А -(ап) т(Т т)е = ----[е(апт+5)(Т-т) -1 - (апт+°)(Т-т)] < 0. (апт + °)2 (апт + °)3 Значит, функция y(t) строго убывает на отрезке [0, Т]. Если ^(0) > к, то уравнение ^(t) = к имеет единственное решение т > 0. В противном случае т = 0. Следовательно, параметр т однозначно единственным образом определяет оптимальные управления. Единственность и теорема 1 доказаны. Следствие 1. Пусть выполнено неравенство ^ [1 - exp(-5T)] >к, (41) тогда на оптимальной траектории N(Т) > 0. Положительность N(Т) вытекает из утверждения 1, дифференциального уравнения (3), начального условия (15) и ограничений на управление (17). Выполнение неравенства (41) определяет экономическую целесообразность разработки газового месторождения оптимальным способом. Существуют другие допустимые стратегии разработки, обеспечивающие положительные прибыли. Такие стратегии являются экономически оправданными, но с худшим результатом. Прибыль у них меньше. Следствие 2. Пусть выполнено неравенство ^ [1 — exp(-5T)] < к, (42) тогда на оптимальной траектории N(t) = 0. Из (42) следует, что месторождение экономически не выгодно разрабатывать, даже оптимальным способом. В завершении данного параграфа приведем алгоритм вычисления максимума прибыли. Для этого достаточно определить параметр т из формулы (18) теоремы 1. Сначала вычисляем ^(0) и сравниваем с величиной к. Если ^(0) < к, то полагаем т = 0. В противном случае для определения единственного решения уравнения р(т) = к можно использовать различные широко известные методы. Наиболее простым из них является метод деления отрезка пополам. В качестве начальных точек можно взять значения 0 и Т.
4. Заключение В настоящей работе исследуется непрерывная агрегированная динамическая расширенная модель освоения газового месторождения с взаимовлияющими скважинами. На базе рассматриваемой модели подвергаются анализу три стратегии освоения газового месторождения. Каждая стратегия разработки сопровождается графиками, представленными на отдельном рисунке. Первая стратегия представляет теоретический интерес, и она связана с попыткой как можно дольше удержать добычу газа на заранее заданном уровне. Было показано, что такой временной период конечен. Данный факт объясняется наличием ограниченного запаса газа. В конце всего временного периода количество всех действующих в разработке скважин стремительно неограниченно увеличивается, что практически невозможно. Во второй стратегии анализируется динамическое поведение добычи на газовом месторождении. Модель исследуется на двух этапах. На первом этапе разработки действующий фонд скважин, начиная с нулевого значения, меняется по линейному закону с постоянным темпом. Выявлены и обсуждены характерные особенности такой разработки. При исследовании третьей стратегии учитывается пропускная способность трубопровода. Действующий фонд скважин меняется по линейному закону на всем рассматриваемом временном периоде. Разработка месторождения состоит из трех этапов: этап возрастающей добычи, этап постоянной добычи и этап падающей добычи. На первом и последнем этапах общий фонд скважин совпадает с действующим фондом. На втором этапе не все скважины задействованы в разработке, появляется резервный фонд. Найдены формулы для описания начала и конца этапа постоянной добычи. Также найдено максимальное значение резервного фонда скважин. Последняя часть работы посвящена решению оптимизационной задачи на максимум прибыли с учетом коэффициента дисконтирования. Рассматриваемая задача является задачей оптимального управления со смешанными ограничениями. Применять в этом случае принцип максимума Понтрягина в классической формулировке не правомочно. Для решения этой задачи был использован принцип максимума Понтрягина в форме Эрроу. Для решения задачи на максимум прибыли было найдено оптимальное управление и доказана его единственность. Предложен алгоритм поиска оптимального решения. В заключительной части работы был получен критерий, определяющий экономическую целесообразность разработки газового месторождения.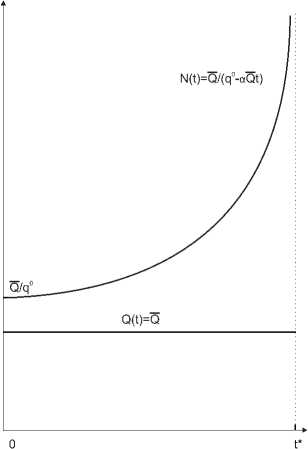
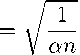
Список литературы Оценка экономической целесообразности разработки газового месторождения
- Вяхирев Р.И., Kopomaee Ю.П., Кабанов Н.И. Теория и опыт добычи газа. Москва : Недра, 1998.
- Хачатуров В.Р., Соломатлт А.Н., Злотов А.В. \и др.]. Планирование и проектирование освоения нефтегазодобывающих регионов и месторождений: Математические модели, методы, применение / под ред. В.Р. Хачатурова. Москва : УРСС : ЛЕНАНД, 2015.
- Маргулов Р.Д., Хачатуров В.Р., Федосеев А.В. Системный анализ в перспективном планировании добычи газа. Москва : Недра, 1992.
- Skiba А.К. Dvnamic model analvsis of gas deposit developments // 2018 Eleventh International Conférence Management Of Large-Scale System Development (MLSD). IEEE Conférence Publications, IEEE Xplore Digital Librarv. P. 619-622.
- Skiba A.K. Maximization of the Accumulated Extraction in a Gas Fields Model. Evtushenko Y., Jacimovic M., Khachav M., Kochetov Y., Malkova V., Posvpkin M. (eds), Int. Conf. on Optimization and Applications (OPTIMA 2018) // Communications in Computer and Information Science. Springer, 2019. V. 974. P. 453-469. DOI 10.1007/978-3-030-10934-9J52.
- Скиба, A.K. Поиск в модели газовых место рождений максимальной длины их общей «полки» // Труды МФТИ. 2019. Т. 11, № 2(42). С. 49-61.
- Эрроу К. Применение теории управления к экономическому росту// Матем. экономика. Москва : Мир, 1974. С. 7-45.
- Понтрягин Л. С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. Москва : Наука, 1976.
- Skiba A.K. Optimal Growth with a Convex-concave Production Function // Econometrica. 1978. V. 3(46). P. 527-539.
- Ли Э.Б., Маркус Л. Основы теории оптимального управления. Москва : Наука, 1972.
- Моисеев Н.Н. Элементы теории оптимальных систем. Москва : Наука, 1975.


