Оценка эксплуатационного состояния тяговых силовых трансформаторов с использованием таблиц решений при нечетких входных параметрах

Согласно стратегии развития ОАО «РЖД» до 2025 г., планируется произвести строительство 60 новых и техническое перевооружение существующих 359 тяговых подстанций (ТП) [1]. В связи с этим возросли требования к системе оценки текущего состояния электрооборудования (ЭО). Очередность технического обслуживания и ремонта (ТОиР) осуществляется путем оценивания текущего состояния электрооборудования ТП [2].

Состояния каждого энергообъекта (трансформаторов, воздушных линий, контактной сети, распределительных устройств) классифицируются таким образом: N – не требуется вмешательства в эксплуатацию ЭО в предстоящий период; A – требуется вмешательство без отключения оборудования в ближайшее время; В – требуется проведение ТОиР с отключением оборудования в течение предстоящего периода; R – требуется вывод ЭО из работы для ТОиР.

Для всего парка энергообъектов составляют списки с оценками текущего состояния и разрабатывают графики ТОиР на квартал и на год.

Для принятия управляющих решений в процессе эксплуатации энергообъектов используют результаты мониторинга основных параметров ЭО, например данные хроматографического анализа трансформаторного масла.

Принимая во внимание неопределенность параметров и неполноту сведений об условиях эксплуатации конкретного ЭО, считаем обоснованным использовать таблицы решений с нечеткими входными параметрами [3-5]. Такой подход становится необходимым дополнением к таблицам решений, чтобы учесть неопределенность диагностических параметров в процессе эксплуатации энергообъектов тяговой подстанции.

Метод оценки эксплуатационного состояния силового трансформатора

Таблицы решений (ТР) получили большое распространение в исследовании операций, системном анализе и для математического обеспечения ЭВМ как удобное средство, позволяющее четко и просто описывать сложные ситуации. Описывая как саму задачу, так и необходимый для ее решения алгоритм, ТР в наглядной форме позволяют определять, какие условия должны быть выполнены, прежде чем можно будет переходить к тому или иному эксплуатационному действию [4]. Таблицы решений – способ компактного представления модели со сложной логикой. ТР в простой форме могут демонстрировать связь между множеством независимых условий и действий.

Применяются различные формы записи ТР. Рассмотрим табл. 1.

Строка (или группа) в табл. 1 является основным импликантом для текущего состояния энергообъекта.

Таблица 1. Один из видов таблицы решений

Table 1. Main view of the solution table

Строка	Варианты условий (диагностических параметров)				Возможные действия после классификации состояния энергообъекта
	Y 1	Y 2	Y 3	Y 4
1	y 11	y 12	y 13	y 14	N
2	y 21	y 22	y 23	y 24	A
3	y 31	y 32	y 33	y 34	B
4	y 41	y 42	y 43	y 44	R

Теория нечетких множеств (ТНМ) представляет собой математический аппарат для работы с объектами, не имеющими жестких, однозначно задаваемых границ. Она позволяет формально описывать нестрогие, нечеткие, расплывчатые понятия и производить с ними различные операции. Применение ТНМ дает возможность формализовать процесс принятия решений в процессе эксплуатации при нечетких условиях [6-9].

Л. Заде ввел понятие лингвистической переменной [6], значениями которой являются слова или предложения естественного языка, которые описывают нечеткими значениями. Сегодня существуют достаточно четкие области, где классификация, а само собой и принимаемые решения, будут достаточно однозначными – область, близкая к идеальному состоянию ЭО, и область, близкая к полному износу ЭО [7]. Принимать решение сложней всего, когда состояние ЭО находится в переходном режиме между этими двумя крайними состояниями и когда этот переход не скачкообразен, а непрерывен. Такая ситуация типична для реально действующих систем, и многие понятия естественного языка не могут быть формализованы с помощью классических математических понятий, так как граница между двумя классифицируемыми состояниями (например, «новый» – «старый») является нечеткой, размытой [7].

Нечеткое подмножество А множества Х характеризуется функцией принадлежности m: Х →[0,1] ставит в соответствие каждому элементу х ∈ X число μ А (х ) из интервала [0,1], характеризующее степень принадлежности элемента х подмножеству А . Причем 0 и 1 представляют собой соответственно низшую и высшую степени принадлежности элемента к определенному подмножеству.

Таким образом, основное предположение состоит в том, что нечеткое множество, несмотря на расплывчатость его границ, может быть точно определено путем сопоставления каждому элементу х числа, лежащего между 0 и 1, которое представляет степень его принадлежности к А .

Над нечеткими множествами можно выполнять различные теоретико-множественные операции:

пересечения С = АоВ, jti_c(x) = //Дх) & //_д (х);

объединения С = A иВ , ц_с^ = //Дх) v //Дх);

дополнения С = А, /z_c(x) = l-/z^(x).

В работах [10, 11] был разработан метод так называемых треугольных нечетких чисел (ТНЧ), представляющих собой нечеткие числа с функцией принадлежности (ФП) в треугольном виде (рис. 1).

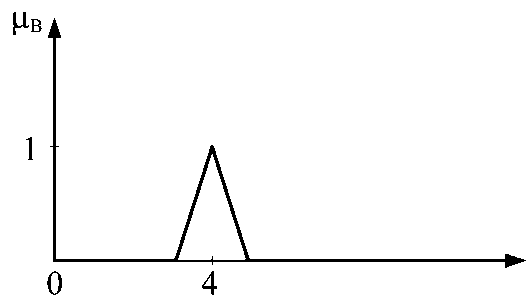
Рис. 1. Пример нечеткого множества. Пусть B -нечеткое число около 4

Fig. 1. Example of a fuzzy set. Let B be a fuzzy number about 4

Треугольное нечеткое число, которое часто обозначается A = ( a 1 , a 2 , a 3 ), определено следующей функцией принадлежности:

Ма(х) = -

(х-а^/^-а,) (а₃-х)/(а₃-а₃) О

если ^ < х < а2, если си < х < а3, если х<сц или х > а3.

Вычисление α - сечения A α треугольного нечеткого числа выполняется по выражению

Aa = [ ai + а( a 2 - a i ) a 3 — а(a 3 — a 2 )]. (2)

Каждый энергообъект получает оценки степени принадлежности к состояниям N , А, В, R в соответствии с данными мониторинга диагностических параметров {у ij }. Для этого используют функции принадлежности, показанные на рис. 2. Такие функции строят для каждого диагностического параметра. Здесь: Z – нулевой уровень, L – низкий уровень, М – средний уровень, Н – высокий уровень значения параметра. Если увеличение значения параметра у ij свидетельствует о деградации состояния, то Z отвечает нормальному состоянию N , L – состоянию А, М – В, Н – R . Если уменьшение значения параметра свидетельствует о деградации, тогда Z отвечает состоянию R , L – состоянию В, М – А, Н – N . Значения функции принадлежности μ k (у i ) лежат в интервале [0; 1]. Функции имеют треугольную или линейную форму с перегибом (горизонтальный участок вне рабочего отрезка значений параметров).

Пример. Для оценки текущего состояния силового трансформатора была выбрана тяговая подстанция «Кача». В табл. 2 приведены значения диагностических параметров для тягового трансформатора ТП «Кача». Количество наблюдений равно 7 ( j = 1,...,7), количество параметров – 7 ( i = 1,...,7).

Критические и нормальные значения параметров взяты из справочной литературы [12] и приведены в табл. 3 [ y i ] k k = 8,9,10,11 для абсолютно уверенного диагностирования k -го состояния объекта (при этих значениях параметров функция принадлежности имеет максимум μ k (у i ) =1).

Если произведены измерения и получен ряд значений [у i ] j , j = 1,…,7 для объекта или наблюдения j , причем, возможно, некоторые измерения отсутствуют, то ряд [у i ] k образует таблицу оценок [μ X ( y i )] k , а ряд [ y i ] j – таблицу [μ X ( y i )] j . Ниже приводятся две такие таблицы (табл. 4, 5) для рядов параметров и результатов наблюдений.

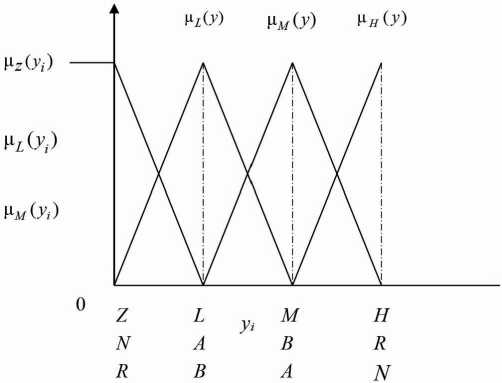
Рис. 2. Функции принадлежности диагностических параметров

• Fig. 2.    Functions of belonging of diagnostic parameters

Таблица 2. Результаты мониторинга параметров трансформаторного масла

Table 2. The monitoring results of parameters of transformer oil

Номер наблюдения	Дата анализа	Значения входных параметров у
		СО 2 , %	СН 4 , %	C 2 H 6 , %	С 2 Н 4 , %	С 2 Н 2 , %	CO, %	tgδ, %
1	28.01.19	0,098	0,0023	0,0012	0,009	0,0188	0,0137	0,15
2	25.02.19	0,107	0,0023	0,0012	0,0102	0,0194	0,0134	0,55
3	04.03.19	0,106	0,0024	0,0012	0,0102	0,0189	0,0146	1,15
4	20.05.19	0,135	0,0016	0,0011	0,0095	0,0175	0,0143	0,68
5	20.06.19	0,156	0,0013	0,0010	0,0083	0,0143	0,0193	0,88
6	19.07.19	0,150	0,0012	0,0009	0,0076	0,0125	0,0140	0,30
7	20.09.19	0,156	0,0009	0,0008	0,0069	0,0101	0,0159	0,53

Таблица 3. Ряды критических значений эксплуатационных параметров трансформаторного масла

Table 3. Series of critical values of operational parameters of transformer oil

& я о 2 к ^	Критические и нормальные значения параметров у
	СО 2 , %	СН 4, %	C 2 H 6 , %	С 2 Н 4 , %	С 2 Н 2 , %	CO, %	tgδ, %
	1	2	3	4	5	6	7
8	Критические уровни для состояния B (необходима смена масла)
	0,07	0,003	0,003	0,001	0,0002	0,03	3,0
9	Критические уровни для состояния R (необходим ремонт)
	0,2	0,01	0, 005	0,01	0,01	0,05-0,06	5,0
10	Критические уровни для состояния A (необходимо внимание)
	0,05-0,06	0,001	0,001	0,005	0,0001	0,015	1,0
11	Нормальные уровни параметров (состояние N )
	0,01	0,00013	0,0001	0,0002	0,00005	0,007	0,05

Таблица 4. Результаты наблюдений параметров [μ _X ( y_i )]₁

Table 4. The results of observations [μ X ( y i )] 1

i	1	2	3	4	5	6	7
H	0	0,4	0	0	0	0	0,857
M	0	0	1	0	0	0,857	0,14
L	0,14	0	0	0,7	0	0,14	0
Z	0,857	0,57	0	0,28	1	0	0

Таблица 5. Нормальные уровни параметров [μ X ( y i )] 11

Table 5. The results of observations [μ X ( y i )] 11

i	1	2	3	4	5	6	7
H	0	0	0	0	0	0	0
M	0	0	0	0	0	0	0
L	0	0	0	0	0	0	0
Z	1	1	1	1	1	1	1

Таблица 6. Таблица решений для состояния N

Table 6. Solution table for state N

Состояния трансформатора при уровнях параметров	Функции принадлежности параметров μ X ( yi )							Выход μ X ( y i ) ср
	1	2	3	4	5	6	7
R ( Z )	0	0	0	0	0	0	0	0
B ( L )	0	0	0	0	0	0	0	0
A ( M )	0	0	0	0	0	0	0	0
N ( H )	0	0,57	0	0	0	0	0,857	0,204

Накладывая таблицу [μ X ( y i )] 1 на [μ X ( y i )] 11 , отмечаем совпадение ненулевых элементов. Чем больше число совпадений, тем больше уверенность в том, что объект близок к состоянию 11, т.е. к N . Необходимо оценить степень уверенности. Для этого вычисляем в каждой клетке совмещенной таблицы степень принадлежности для пересечения размытых множеств X j и X k , которая определяется как минимум из μ X ( y i ) j и μ X ( y i ) k , и строим таблицу [μ X ( y i )] jk :

НД)Л = min(^(y,)y, М.Ш.                       (3)

Например, наложив приведенную выше таблицу [μ X ( y i )] 1 на [μ X ( y i )] 11 , получим таблицу решений [μ _X ( y_i )]_1,11 следующего вида (табл. 6).

При этом наложении отмечаем две точки совпадения лингвистических оценок. Мерой совпадения в каждой точке является степень принадлежности и уij ,и уik в этой точке к одному – 726 – и тому же множеству (любому из множеств Н, М, L, Z). Это значит, что эта мера представляет собой меру принадлежности к объединению нечетких множеств в каждой точке. Функция принадлежности к объединению в каждой точке совпадения i определяется как

Цл U) = max_YX [(Ц _v (x), ц_г (у)) ]_; , (4) здесь Y и X – лингвистические переменные для точки i ; μ X ( yi ) – мера совпадения значений параметра i (результата измерения или наблюдения) и критического значения (признака).

Для нашего примера значения μ X ( y i ) составят: 0; 0,57; 0; 0; 0; 0; 0,857; что в среднем дает μ X ( y i ) ср = [0,57+ 0,857]/7= 0,204. Это означает, что уверенность заключения о возможности состояния N объекта при наблюдении № 1 составляет около 20,4 % при семи критериях за выбранный период времени.

Аналогичным образом можно оценить возможности остальных состояний по всем наблюдениям. Значения функции принадлежности в соответствии с линейным характером ее изменения на отрезке между критическими значениями параметра вычисляют по следующим формулам:

V. (X)< V _z< V. (У), то Ц_у (у,), = [y_y.-у_ (X)] / [у, (У)-у, (X)];

I и I (5)

Ц.г(у)7=1-Цг(у)7;Х(У)еХ,45,Х

Когда наблюдения относятся к парку трансформаторов, то можно с помощью оценок уверенности сформировать списки и установить очередность обслуживания и ремонта. Если наблюдения относятся к различным моментам (датам) «жизни» одного трансформатора, то можно построить графики изменения уверенности в классификации состояний (рис. 3–6) и по ним прогнозировать остаточный ресурс, задав критические значения уверенности в необходимости производства ТОиР.

Таким образом, за отчетный период наблюдений для состояний A, В и R будут соответствовать следующие таблицы решений (табл. 7 – 9).

По приведенным графикам изменения уверенности состояний (рис. 3–6) можно утверждать, в какие периоды и в каком состоянии находились измеряемые параметры, превышали они допустимую норму или же нет, в какой момент состояние стабилизировалось. Например, рассматривая график уверенности состояния N (рис. 3), можно сказать, что за отчетный

Таблица 7. Таблица решений для состояния A

Table 7. Solution table for state A

Состояния трансформатора при уровнях параметров	Функции принадлежности параметров μ X ( yi )							Выход μ X ( y i ) ср
	1	2	3	4	5	6	7
R ( Z )	0	0	0	0	0	0	0	0
B ( L )	0	0	0	0	0	0	0	0
A ( M )	0	0	1	0	0	0,857	0	0,265
N ( H )	0	0	0	0	0	0	0	0

Таблица 8. Таблица решений для состояния B

Table 8. Solution table for state B

Состояния трансформатора при уровнях параметров	Функции принадлежности параметров μ X ( y i )							Выход μ X ( y i ) ср
	1	2	3	4	5	6	7
R ( Z )	0	0	0	0	0	0	0	0
B ( L )	0,14	0,56	0	0,7	0	0,14	0	0,220
A ( M )	0	0	0	0	0	0	0	0
N ( H )	0	0	0	0	0	0	0	0

Таблица 9. Таблица решений для состояния R

Table 9. Solution table for state R

Состояния трансформатора при уровнях параметров	Функции принадлежности параметров μ X ( y i )							Выход μ X ( y i ) ср
	1	2	3	4	5	6	7
R ( Z )	0,857	0	0	0,28	1	0	0	0,305
B ( L )	0	0	0	0	0	0	0	0
A ( M )	0	0	0	0	0	0	0	0
N ( H )	0	0	0	0	0	0	0	0

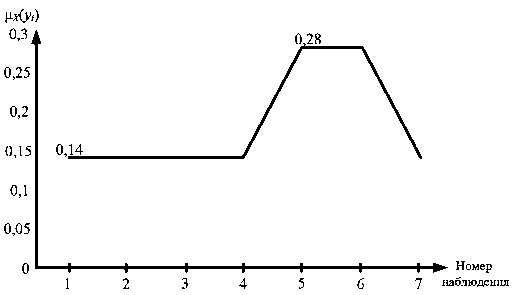
Рис. 3. График изменения уверенности состояния N

• Fig. 3.    Graph of changes in the confidence state N

период не были превышены критические значения уверенности для данного состояния оборудования [2, 12] и нет необходимости в проведении ТОиР. Если значения параметров превышают «норму», т.е. величины, которые можно ожидать за счет естественного старения, то через некоторое время (5 – 10 дней) повторно отбирают пробу масла и проводят анализ. В случае превышения критических значений следует ТОиР. Из полученных таблиц (табл. 6-9) для нашего примера, при наблюдении семи критериев за выбранный период времени, для каждого состояния приводится возможная уверенность его существования. Так, для состояния N она составляет около 20,4 %, для состояния A – 26,5 %, для состояния B – 22,2 %, для состояния R – 30,5 %.

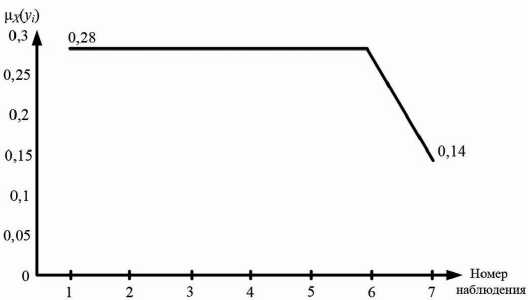
Рис. 4. График изменения уверенности состояния A

Fig. 4. Graph of changes in the confidence state A

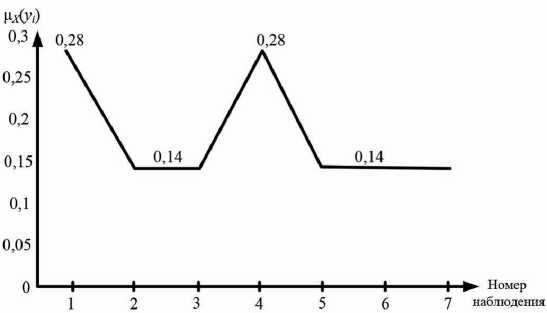
Рис. 5. График изменения уверенности состояния B

Fig. 5. Graph of changes in the confidence state B

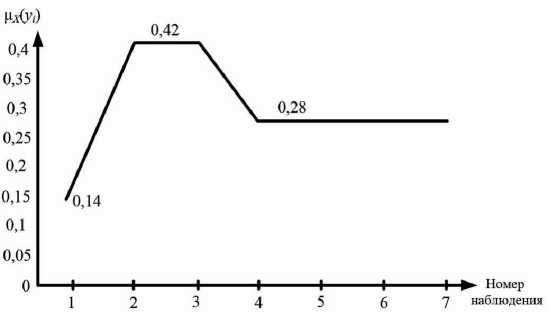
Рис. 6. График изменения уверенности состояния R

Fig. 6. Graph of changes in the confidence state R

Заключение

Рассмотренный выше метод оценивания состояния ЭО может быть положен в основу программного обеспечения экспертной системы для службы эксплуатации высоковольтного оборудования тяговых подстанций железнодорожного транспорта. Информация о результатах текущих испытаний и измерений параметров ЭО регулярно вводится и обрабатывается на компьютерах работниками службы эксплуатации. Инженеры по ЭО ТП, воздушным линиям и контактной сети получают оценки уверенности в идентификации состояния каждого поднадзорного энергообъекта по мере поступления новых сведений. На основе этих оценок составляют и корректируют план текущих и капитальных ремонтов.

Предполагается, что такая экспертная система позволит сократить трудовые и материальные затраты на ТОиР и обеспечить надежность старого оборудования.