Оценка эрозионной стойкости упрочненных металлических сплавов в условиях каплеударного воздействия

Введение. Единичный удар водяной капли по металлической поверхности выглядит довольно безобидным и не может причинить ей большого вреда. Однако при длительном циклическом воздействии капель с частотой соударений 50…200 с ^- 1 и скоростью 150…600 м/с происходит стремительное эрозионное разрушение металла . На практике условия каплеударной эрозии формируются при наличии конденсата в парогазовых средах, что приводит к прогрессирующему износу лопастей парогазотурбинного и компрессорного оборудования. Несмотря на актуальность проблемы и её активное изучение [ 1 – 5 ], к настоящему времени физическая природа инициации износа при ударно - капельном воздействии до конца не ясна. Сложность анализа обусловлена тем, что каплеударное воздействие включает несколько составляющих: механическую (усталостную), кавитационную (гидродинамическую и пузырьковую) и коррозионную [ 6 – 10].

Кинетика эрозионного износа включает несколько стадий [ 11, 12 ]. Первая из них, инкубационная, характерна тем, что признаков разрушения и потери массы металла на этой стадии ещё нет. Поэтому длительность инкубационного периода обычно принимается в качестве антиэрозионного свойства материала в условиях каплеударного воздействия.

В ряде работ [ 8, 13 – 17] авторами исследованы особенности этого явления в таких пластичных металлических материалах, как однофазные титановые сплавы, сталь с аустенитной или сорбитной структурой. Начало изнашивания в этом случае определяется развитием подповерхностной усталостной пористости (рис. 1, a ), возникающей в металле в зоне соударения по механизму перколяции [ 18, 19] с последующим слиянием пор и формированием первичных поверхностных эрозионных кратеров износа (рис. 1, b ). В этом случае кратеры имеют характерную морфологию с весьма разветвленной поверхностью .

• а )                                                                  b)

Рис. 1. Зарождение износа при каплеударной эрозии образцов аустенитной стали 08Х18Н10Т (РЭМ): а — формирование усталостной пористости в месте соударения (сечение образца по глубине); b — образование первых эрозионных кратеров (эрозионная дорожка на поверхности образца)

Fig. 1. Origin of wear under drip erosion of samples of austenic steel 08Cr18Ni10Ti (SEM): a – formation of fatigue porosity at collision site (cross section of the sample in depth); b – formation of the first erosion craters (erosion track on the sample surface)

Машиностроение и машиноведение

Морфологические особенности такого износа и его расчетно - аналитическая модель, разработанная на принципах усталостной теории Гудмена, наиболее полно представлены в работе [8]. В упрочненных же металлических материалах механизм перколяции не может быть реализован, так как размер зон пластичности слишком мал. В этом случае усталостная пористость не образуется, а морфология первичных кратеров износа определяется механизмом зарождения, роста и ветвления хрупких (скольного типа) усталостных трещин. Отличительными признаками такого механизма зарождения эрозионных кратеров являются сравнительно гладкая (фасеточная) поверхность их стенок (рис. 2, а) и наличие трещин в поперечном сечении кратеров (рис. 2, b).

Рис. 2. Эрозионные кратеры на поверхности образца мартенситной стали 20Х13 (РЭМ)): а — стенка первичного кратера с ветвящейся острой трещиной;

b — поперечное сечение кратера с усталостными трещинами

Fig. 2. Erosion craters on the surface of sample of martensitic steel 20Cr13 (SEM)): a – wall of primary crater with sharp branching crack;

b – cross section of crater with fatigue cracks

Исходя из анализа вышеупомянутых экспериментальных данных была сформулирована цель настоящей работы — нахождение закономерностей и создание расчетно - аналитической модели эрозионного износа рассматриваемых материалов. Параллельно решалась задача критериальной оценки материалов, с помощью которой можно было бы отнести их к пластичным или прочным и использовать соответствующую модель механики усталостного разрушения.

b)

Использование диаграмм предельных состояний материала в расчетной модели. Анализ базы экспериментальных данных, полученных в результате стендовых эрозионных испытаний образцов сталей с различной структурой, позволяет рекомендовать их диаграммы предельных состояний в качестве классификационного критерия пластичных и прочных материалов. В механике разрушения диаграмма предельных состояний определяет зоны хрупкого и вязкого разрушения материала. Общий вид такой диаграммы представлен на рис. 3 , где продемонстрировано предельное состояние по временному сопротивлению σ _В в соответствии с теорией пластичности (наклонная прямая 1) и предельные состояния в соответствии с линейной механикой разрушения (кривые 2 и 3). Диаграмма на рис. 3 нуждается в некоторых комментариях, поскольку, применительно к исследуемой нами проблеме, отличается от своих классических предшественников.

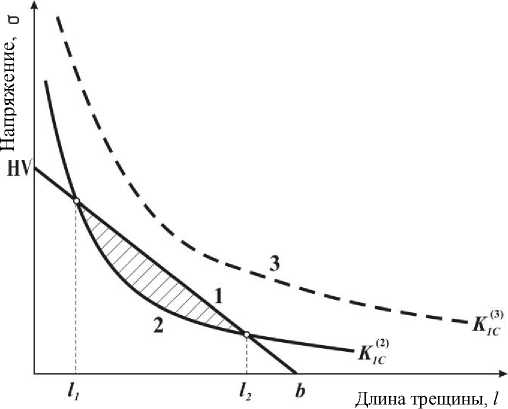
Рис. 3. Общий вид диаграммы предельных состояний с линиями предельных (1) и критических (2, 3) напряжений

Fig. 3. General form of limiting states diagram with lines of limiting (1) and critical (2, 3) stresses

В фундаментальной работе [2 0, C. 23] доказано, что для различных видов нагружения как при пластическом, так и при хрупком разрушении трещиностойкость К 1С определяется временным сопротивлением (пределом прочности) материала а В и конструктивным размером образца b (например, толщиной или шириной пластины):

откуда b = —2— , ^а в

где К 1С — критический коэффициент концентрации напряжений для трещины скольного типа (хрупкая трещина типа I).

Выражение (1) универсально, поскольку выведено для наиболее общих и простых случаев — неограниченного полупространства по глубине материала и неограниченной плоскости поверхности образца. Оно справедливо как для случая поверхностной трещины, распространяющейся в глубину, когда ограничивающим размером является толщина образца, так и для центральной (внутренней) трещины, растущей вдоль своей оси, когда ограничивающим размером b является ширина образца.

С учетом выражения (1) линия предельного состояния 1 на рис. 3 определяется как:

^а в Y

2 ■ K i c )

а p ( l ) = HV ■ 1 -

В выражении (2) учтено, что рассматриваемые процессы каплеударного воздействия локализованы на поверхности материала. Все возникающие при этом трещины являются поверхностными (т. е. направлены в глубину образца либо от его поверхности, как на рис. 2, а, либо от поверхности кратера, как на рис. 2, b ). Когда трещина достигает некоторого определенного макроразмера (например, l 2 или b ), все процессы, определяющие её продвижение, локализованы в вершине трещины . В этом случае эти процессы происходят на некоторой глубине от поверхности и использование в расчетах такой макроскопической (т. е. объемной) характеристики, как а В в выражениях (1) и (2), с физической точки зрения оправдано. Когда же рассматривается процесс поверхностного зарождения трещины (например, l 1 ) , необходимо учитывать поверхностные эффекты (например, поверхностное натяжение или силы отображения, действующие на дислокации), которые требуют дополнительной работы зарождения по сравнению с работой зарождения трещины в объеме материала. В этом случае предельное состояние материала должно характеризоваться более высоким уровнем напряжения, чем а В . Такой более высокий уровень напряжений на диаграмме предельных состояний для поверхностной трещины задан в

Машиностроение и машиноведение

выражении (2) и на рис. 3 для линии 1 при l =0 значением твердости HV , что соответствует физическому смыслу твердости как поверхностного свойства.

Линии критических напряжений (кривые 2 и 3 на рис. 3) представляют собой степенные функции :

σ _k ( l ) =

K 1 C

Y ⋅ π⋅ l

Высоким значениям К1С соответствует кривая 3, причем хрупкое состояние в этом случае не достигается, так как линии предельных состояний 1 и 3 не пересекаются. На диаграмме предельных состояний аустенит- ной стали 08Х18Н10Т линии не пересекаются, что говорит об отсутствии трещин и позволяет отнести её к пла- стичным материалам с перколяционным механизмам усталостного разрушения в условиях каплеударного изно- са.

Область трещин l 1 - l 2 соответствует хрупкому состоянию при К 1С , отвечающему кривой 2. Из рис . 3 видно, что при уменьшении К _1С , а также с возрастанием значений HV или b (при фиксированном К _1С ) заштрихованная область хрупкого состояния l 1 - l 2 увеличивается. Точки пересечения графиков на рис. 3 по своей физической сущности представляют собой начальный l 1 ≡ l 0 и критический l 2 ≡ l _С размеры трещины. При l0 трещина самопроизвольно не растет, и опасности хрупкого разрушения нет. При l≥ l_С рост трещины необратимо и автокаталитически ускоряется, разрушение (образование кратера эрозионного износа) происходит катастрофически быстро. Такая картина наблюдается, например, на диаграмме предельных состояний стали 20Х13 со структурой мартенсита. Значения l0 и lC в рамках предлагаемой расчетно-аналитической модели находятся путем совместного решения уравнений (2) и (3) для предельных σp и критических σk напряжений для материала, заданного такими свойствами, как твердость HV, предел прочности σВ, трещиностойкость К1С, а также с учетом геометрических параметров трещины Y. Множитель Y характеризует тип трещины и может быть определен из справочников [21]. При этом в зависимости от выбора типа трещины, значения Y могут существенно отличаться и их необходимо согласовывать с экспериментом. Так, например, экспериментальные данные по каплеударной эрозии образцов стали 20Х13 с мартенситной структурой дают: lC=68 мкм — для проекции трещины на поверхности образца и lC=7 мкм — для проекции трещины по сечению образца (по глубине).

Расчетно-аналитическая модель для оценки эрозионной стойкости упрочненных металлических сплавов. В интервале между l 0 и l C скорость роста трещины (в расчете на один цикл нагружения, т. е. на один удар капли) может быть определена на основе теории усталости Пэриса - Эрдогана [ 22] с помощью уравнения Пэриса:

^dl = A Δ K^m                                                (4)

dN

В свою очередь величина Δ К определяется выражением:

Δ K = K max - K min = Δσ π l                                       (5)

с учетом следующих условий:

K _max = σ _max π l и K _min = σ _min π l для σ _min > 0 и K _min = 0 для σ _min ≤ 0

Здесь К — коэффициент концентрации напряжений для соответствующих максимального σ max и минимального σ min напряжений единичного цикла.

Для использования методического аппарата теории Пэриса - Эрдогана необходимо экспериментальное определение параметров уравнения Пэриса m и А , которые являются эмпирическими константами материала. Так, например, выполненные авторами стендовые испытания образцов стали 20Х13 с мартенситной структурой для условий каплеударной эрозии дают значения параметров уравнения Пэриса: m = 2,5 и А = 3,403·10 ^- 9 м/цикл.

В работе [ 8] доказано, что при соударении жидкой капли с металлической поверхностью напряжение σ распределяется по поверхности во времени τ в соответствии графиком на рис. 4 . Величина σ выражена в относительных единицах ρ 0 ·с 0 · V 0 , называемых приближением гидравлического удара. Время τ также имеет относительную шкалу, где ρ 0 — плотность жидкости, с 0 — скорость звука в жидкости при нормальных условиях, V 0 — скорость соударения, R 0 — радиус капли.

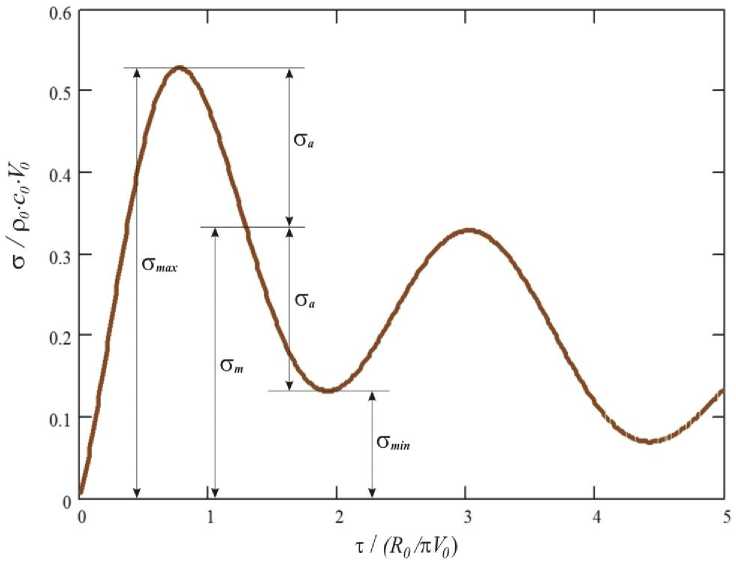
Рис. 4. Расчетные параметры цикла нагружения при капельном соударении

Fig. 4. Calculated parameters of loading cycle in case of drop collision

На рис. 4 отмечены величины напряжений, принятые в теории усталости, в частности в теории Пэриса - Эрдогана (максимальное σ max , минимальное σ min , среднее σ m и т. д.). Однако они требуют уточнения для использования в уравнении Пэриса ( 4 ). На рис. 4 представлено распределение напряжений для однократного соударения, а уравнение Пэриса используется для многоциклового нагружения. При однократном соударении с увеличением времени σ min → 0, поэтому единичный цикл нагружения становится отнулевым. При этом время между соударениями, попадающими в одну точку, превышает время единичного соударения в несколько раз. При отнулевом цикле нагружения в формуле ( 5 ) в соответствии с рис. 4 следует принимать:

Δ σ = σ max = 0,528· ρ 0 ·с 0 · V 0 .                                              (6)

Решением уравнения Пэриса (4) для условий каплеударной эрозии может быть найдено допустимое количество циклов (капельных соударений) NC, определяющее продолжительность инкубационного периода эрозионного износа данного материала:

NClC

N C = ∫ dN =∫ 0               l 0

da

A ⋅ ( ∆ K ) ^m

Строго говоря, полученное интегрированием значение N C не является величиной инкубационного периода каплеударной эрозии m 0 , поскольку не учитывает количество циклов N 3 , необходимых для образования трещины размером l 0 . Поэтому для прикладного использования выражения ( 7 ) необходимы корреляции величины N C с данными стендовых испытаний с учетом того, что m 0 = N 3 + N C .

Машиностроение и машиноведение

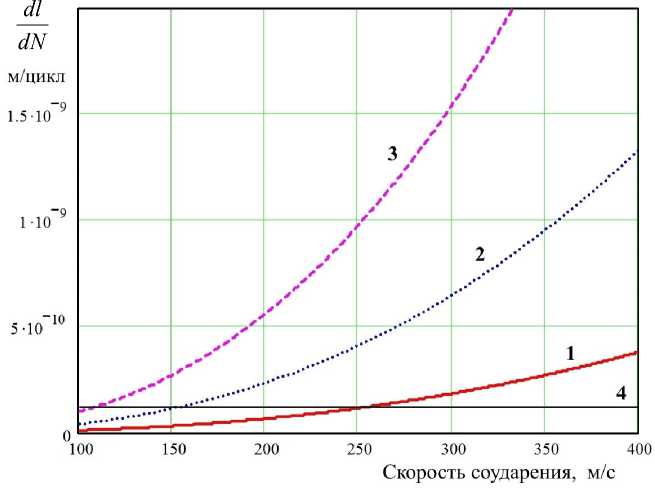
Рис. 5. Зависимость скорости роста трещины в стали 20Х13 с мартенситной структурой от скорости капельного соударения при различных значениях начальной длины трещины: 1 — 0,55 мкм; 2 — 1,5 мкм; 3 — 3,0 мкм;

4 — пороговое значение роста острой трещины

Fig. 5. Dependence of crack growth rate in 20Cr13 steel with martensitic structure on drip collision rate for different values of initial crack length: 1 – 0.55 μm; 2 – 1.5 μm; 3 – 3.0 μm; 4 – threshold value of sharp crack growth

Не вдаваясь в детали данной корреляции, которые выполнены при разработке расчетно - аналитической модели, приведем результат использования теории Пэриса - Эрдогана (4)+(5)+(7) с учетом особенностей каплеударного механизма эрозии (6) на примере стали 20Х13 с мартенситной структурой, представленный на рис. 5. Зависимости на рис. 5 можно рассматривать в качестве прикладного критерия эрозионного разрушения , показывающего минимальное значение скорости соударения, при котором инициируется износ в стали. Если график функции на рис. 5 находится ниже линии порогового значения, то расстояние, на которое трещина продвигается за один цикл нагружения, лежит в области упругих деформаций и упруго релаксирует после снятия нагрузки. В этом случае трещина расти не будет. Так, например, из рис. 5 следует, что, если в мартенсите стали 20Х13 уже есть трещины длиной l 0 = 1,5 мкм (линия 2), то они будут развиваться при скоростях соударения V 0 , превышающих 150 м/с.

Обсуждения и заключение. Представленная расчетно - аналитическая модель формирования износа при каплеударной эрозии упрочненных материалов включает две фактически независимых части. В первой из них путем построения диаграммы предельных состояний материала определяются начальный l 0 и критический l C размеры трещин, которые зависят исключительно от структуры и механических свойств материала ( HV, σ B , K 1C ). Во второй части на основе уравнения Пэриса из усталостной теории Пэриса - Эрдогана рассчитывается предельное количество циклов нагружения (число ударов капель, попадающих в одну точку), которое материал может выдержать до начала формирования износа, соответствующего значению l C . При этом параметры уравнения Пэриса для исследуемого материала должны быть определены из эксперимента. Для приблизительной сравнительной оценки допустимо использовать известные типичные значения параметров, которые приводятся в научной литературе, однако, далеко не все типы материалов изучены с точки зрения использования для них уравнения Пэриса. Поэтому сравнение материалов и использование для них типичных значений (не только параметров уравнения Пэриса) следует проводить с обязательным учетом структурных особенностей.

Предложенный в работе расчетный критерий в виде минимальной скорости соударений , при которой инициируется эрозионный каплеударный износ, можно рассматривать как универсальный для любого материала. Аналогичный критерий был апробирован авторами в работе [8] на основе усталостной модели Гудмена для пластичных материалов, в настоящей же работе он использован для упрочненных материалов и рассчитан на базе модели Пэриса-Эрдогана. Это обеспечивает единое измерительное пространство для материалов, деградация поверхности которых при каплеударной эрозии происходит по принципиально различным механизмам — путем развития хрупких трещин в упрочненных материалах (например, в мартенситной стали 20Х13, рассмотренной в настоящей работе) и путем образования усталостной пористости по механизму перколяции в пластичных V0min. материалах (например, в аустенитной стали 08Х18Н10Т, рассмотренной в работе [8]).