Оценка этапа поиска симплексного инвариантного метода

Часто при решении задачи поиска и отслеживания дрейфующей цели приходится сталкиваться с рядом проблем, обусловленных неполной априорной информацией об объекте. Для решения подобных задач необходимо использовать такие методы, которые обеспечивают самонастройку в процессе работы.

В работе [1] раскрыто прим ен ение посл едовательного симплексн ого метода для решения задачи оптимизации, получены ст атистич еские ха^ра ктеристики пои ска, построены не сколько стратегий и вариантов алго^р итма поиска, р азработана методи ка их практи ческого п р именения в задачах оптимизации реа ль ных объектов. Использование си мплексного инвариант н ого метода (СИМ) и инвариантного комплекс-мето^да (ИКМ) для ре шения зад ач поиска и отслеж иван ия нестационарного экстремума отмечена в и сследованиях [ 2-4]. В этих работах под черкнута эффективность прямых методов поиска при работе в у словиях неп олной априор но й информаци и. Основные принципы построени я инвари антны х к контр ол ир^ уемым возмущения м алгор итмов заключаются в следующем.

• 1.    На каждом шаге поиска k с целью получения оценок градиента a i и оценок зависимости возмущение-выход b j производи тся ап проксимация целевой функции выражением вида

  ⁿ

  Q ( х ( k ), z ( k )) = У

  
  

• 2.    На каждом шаге проис ходит вычитание вкладов возм ущений в целевую функцию:

• 3.    Выбор направления движен ия симплекса в пространст ве происходи т по соотношению скорректированных значений C j .

(a,( k) ■ x,( k)) + £ (b( k) ■ Zi( k)), i=1                                  i=1

здесь x – вектор управля ем ы х переме нных; z – лин еаризованный ве к тор контролируемы х возмущений; k – дискретное время ; n – количество у правляе мы х переменных; m – количеств о контролируемых возмущений.

m

C j^{( k}) = Q ^{( k} I - ]L ( ^b i ⁽ k ) - z^ik », , = 1,..., n + 1,                                  (2)

где C j – скорректирован но е значение целевой фу нкции в j - й вершин е текуще го сим плекса; Q j – измеренные значения целевой функц ии в j -й в ершине текущего си мп лекса.

В работе [5] рассмотрен вар иант структурной а даптации пр^ямого метода поиска. Суть такой адаптации заключает ся в исп ол ьзовании ра зных мод ификаций, в частности комплек с-метода на определенном э тапе поиск а.

В продолжение разраб от ки адаптивных алгор итмов п оиска необходимо рассмотреть подходы, обеспечивающие пара метрическую адаптацию п оисковых ме тодов.

Для СИМ основным управляемым параметром может являться размер его ребра. Неверно выбранный размер ребра мож ет привести к ряд у неблагоприятны х последств ий. На рис. 1 изображены траектории движени я экстр емума и си мплекса в проц ессе поиска и отслеж ивания.

x ₁

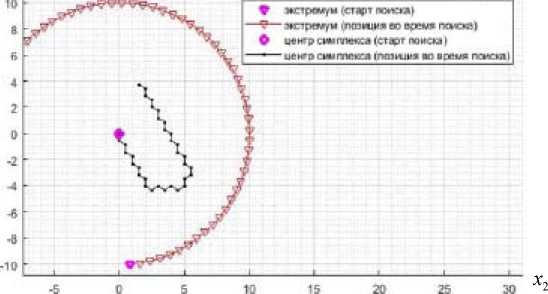
Рис. 1. Отс ле жива^ние экстр е му ма (малы й разме^р ребр а с импл ек^ са)

Fig. 1. Tra ck in^g the ex trem^ u^ m (small si ze of the ed ge o f the sim^ p le x)

x ₂

4       0        5        10       15       20       25       30 x ₁

V wcrpew>w iстарт писав> -~-~^ m- « ^ r.^i ♦ ме^тр ce^iWK-aicnji поним)

---•   ^ewlp СаМГТМКX llinii*#ri* t

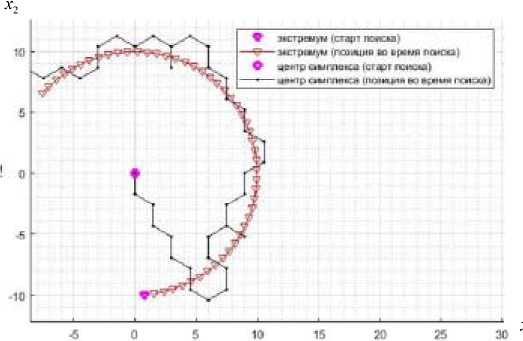
Рис. 2. Отс ле живание экстр емума (боль шой разме р ребра симп лекса)

Fig. 2. Trac^ki ng the ext^rem^ um (big si ze of the ed^ge o f the sim^ ple^ x)

Если размер ребра будет задан небольшим, равным или меньше расстояния, на которое экстремум смещается за одну единицу дискретного времени, то, учитывая исходное отставание, симплекс не сможет настичь цель. На рис. 1 видно, что симплекс выдерживает общее направление движения, но из-за малого размера шага ему не удается догнать цель.

Рассмотрим обратную ситуацию: с заведомо большим шагом поиска (рис. 2).

На рис. 2 в идно, что с имп лекс дост иг дрей фую щего экстр емума, повто ряет ег о трае кто-рию д вижения. Но качество повторения траектории неидеальное: имеют место случаи повторных отражений и закручиваний симплекса вокруг одной из вершин. Это говорит о том, что скорость движения экстремума много меньше скорости движения симплекса, последний вынужден простаивать в околоэкстремальной области, пока экстремум сам не выйдет из текущей зоны локализации симплекса.

Можно пр едп оложить, что существует та кой размер ребра сим плекса, при котор ом он бу -дет отслеживать цель с минимальн ым отстава нием. Также с тоит отметить, что на пе рвом этап е поиска (когда симплекс догоняет ц е ль) размер р е бра долже н иметь в озможн ость уве личиват ь ся до максимально допустимого зн аче ни я, чтобы к ак мож но быстре е достич ь экстр ем альной о б-ласти. Для э того н еобходим о , чт об ы ра змер реб^ра сим плекса самос тояте л ьно изм енял с^я в пр о -цессе по иска и отслеживани я . Законы, по которым могла бы происходить такая самонастройка, неочевидны ввиду малой апр ио рной ин формации о само м объекте.

Цель дан ной работы – ан ализ хара ктеристик, п олучаемых в проц ессе поис ка и отслежива -ния экстремума на предме т выя вления законо мер ностей, кото рые в последс твии можно буд ет использовать для оценива н ия эт апа работы ин вари антного сим плекс -метода .

Пост— за"ач"

Рассмотрим за^дачу п оиска и от слеживания эк стремума н естационарной м одели:

Q (х( k), z( k)) ^ min, ie X где X = {х: х e E",x < x < x +}, x , x+ - позиционные ограничения задачи; En - n-мерное евклидово пространство; x – вектор управляемых п ереме н ных; z(k) – вектор контро лируемых возмущений; k – дискретное врем я.

В качестве ц елевой фун кц ии п р и мем мод е ль с ле^д у ющего в ида :

Q ( х ( k ), z( k )) = z ( k) + ( x 1 ( k ) - R sin( ® • z ( k ))) 2 + ( x 2 ( k ) - R cos( ® • z ( k)))²,    (4)

где z ( k ) = v q · k , v q – скор ость вертика льного дрейфа экстремума; R – радиус траектории э кст^ре -му ма (горизонта льной составл я юще й); ω – угл ов ая ско рость дрей ф а э кс тр е му ма.

Такой выбор модели обу^словлен тем, что в т р аектории движени я экстре мума будут как го-ризонтальна^я, так и вертика льная состав ляю щие. П^ричем напра вление гор изонтальног о дрей -фа будет в течение про цесса пои ска постоя нно м е нят ься.

Зададим параметр ы модели таки м обр аз ом, чт о б ы экстр емум за о^дну еди ницу диск^{^} р етно-го времени смещался в горизонтал ьн ой плос ко сти п рост ран ств а поис ка н а ра ссто_^яние, р авное единице, други ми словами , ско_^ро ст ь дре йф а э к стрем у м а в г ор изонтальн о й пло с к^{^}о с ти буде т равна v x = 1. Это позво лит пр едста вл ять ин формацию о размере реб^ ра симплекса и его скор ости движения с разу в от ношении к ф ак^тическо й с корости дрейфа ц ели .

Угловую скорость гор изонталь^ной состав ляюще й дрей фа мож но в ыразить че рез радиус окружности, описываемой траектор ией, и скор остью горизо нтальн о й сос тавляюще й дрейфа:

ю = arccos I 1 -

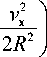
Таким образом, при условии , что v x = 1, п араметры мо^дели п римем след ующим и: v q = 1 ; R = 50; ω = 0.02.

Условимся, что поиск стартует вдали от экстремума. Так как горизонтальная составляющая траектории движения экстремума пре^дстав ляет со бой окруж ность, то б^удет логичным , что бы симплекс стартовал из равноудале нной от трае ктории др ейфа точки – центра этой о кружно сти ( x 1 = 0, x 2 = 0). Количество шаг ов поис ка огранич им значени ем K = 300.

Иссл едование х арактеристик

Проведем несколько эксп ериментов с раз ным размеро м р ебра с имплекс а. Рассмотрим несколько характеристик, полученных во время п оиска:

• -    значения целевой функции на кажд ом шаге Q ( k ) ;

• -    максимальное количество закручиваний вокруг одной из вершин симплекса на каждом шаге M ( k ).

Дополнительно построим график отставания центра тяжести симплекса от цели на каждом шаге E ( k ).

Для первого эксперимента примем ребро симплек ^ са L = 1 ( рис. 3). В таком слу чае ск ^ орост и движения симплекса вдоль координат x 1 и x 2 будут, соответственно, следующими:

rx =y = 0.5,(6)

r = LU » 0.58, x2       3

что меньше скорости д вижения оптимум а в горизон тальной п ло скости v x = 1.

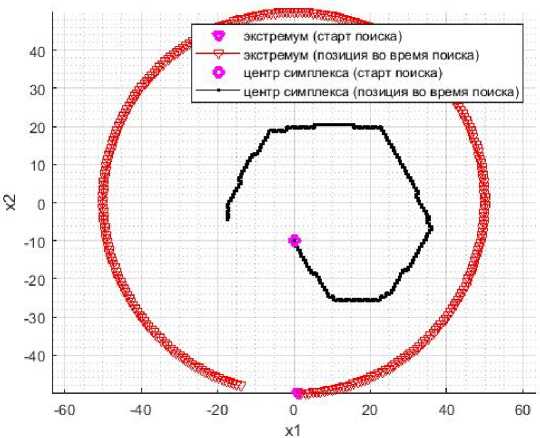
Рис. 3. Траек то рии движен ия экстрем ума и симп ле кса (малый размер ребра симпл екса)

Fig. 3. Trajec to ries of e xtrem^ u m and sim^plex moveme nts (small s ize of t^he e dge of the si m^plex^)

На рис. 4 видно, что зависи мость Q (зна^{^}чения целев ой функц ии^{^}) повторяет ха^{^} рактер зависимости отставания симплекса о т цели E . Зна^{^}чен ия Q уменьша ли сь одно вр емен но с сокращением расстояния до экстремум а и росли с его увелич ением. Дл я симпл екс а критери ем закручивания вокруг одной из верши н [1] является превышение этим параметром значения

M >  1.65 n + 0.05 nn

или для текущего случая при n = 2

M > 3.5.

При проведении предыдущего эксперимента было зарегистрировано несколько случаев чрезмерного закручивания симплекса, но в целом количество последовательных вращений вокруг одной и той же вершины симплекса не превышало значения 3. Это говорит о том, что симплекс не локализовался в процессе поиска – все время происходило его движение.

На рис. 5, 6 показаны результаты эксперимента с размером ребра L = 4, дающим скорость перемещения симплекса выше, чем скорость горизонтального дрейфа v _x = 0.8: r_{x 1} = 2, r_{x 2} ≈ 2.3.

На рис. 6 заметно влияние чрезмерного закручивания на расстояние до экстремума – в то время, когда симплекс вращается на месте, экстремум успевает удалиться. Также в некоторой степени влияние закручивания распространяется на характеристику Q – на графике в те же моменты времени наблюдаются небольшие скачки.

В данном эксперименте симплекс достигает своей цели примерно к 25-му шагу, что можно увидеть на графике отставания. Характеристика Q на этом этапе также имеет схожий характер изменения. После того как симплекс достиг экстремальной области, во время следования за оптимумом периодически происходит чрезмерное закручивание симплекса. Можно предположить, что это связано с тем, что размер шага симплекса много больше шага экстремума и первый вынужден простаивать в некоторой локации до тех пор, пока оптимум не выйдет за ее пределы.

Если увеличить количество шагов поиска до K = 1000, характеристики будут иметь следующий вид (рис. 7).

После достижения околоэкстремальной области симплекс поддерживает некоторый минимальный разрыв с целью, значения Q плавно растут – это свидетельство наличия вер-

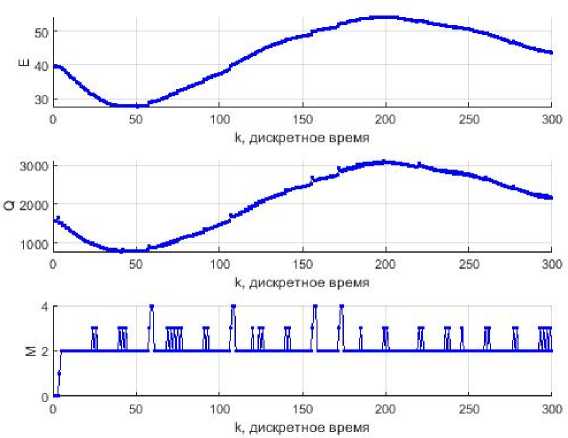
Рис. 4. Характеристики процесса поиска (малый размер ребра симплекса)

Fig. 4. Characteristics of the search process (small size of the edge of the simplex)

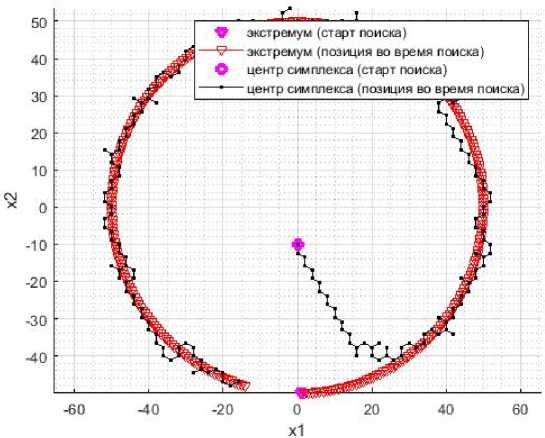
Рис. 5. Траекто р ии движени я экстрем ума и симп ле кса (больш ой разме^р ребра симп лекса)

Fig. 5. Traje cto ries of extre mu m and sim^plex movem ent (b ig siz e of the e dg e of the s im^plex^)

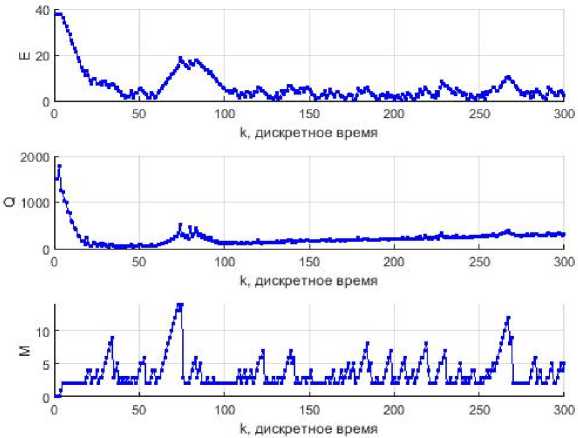
Рис. 6. Характеристики процесса поиска (большой размер ребра симплекса)

Fig. 6. Characteristics of the search process (big size of the edge of the simplex)

тикального дрейфа целевой функции. Время от времени происходит закручивание симплекса.

Полученной информ ации дос таточно, чтоб ^ ы сделать вывод о то м, что на разны х этапах поиска и при раз н ых ра змерах р ебра си мплекса хара ктеристик а Q им еет отличительные признаки. Следовател ьно, мо ^ жно допусти ть, что по сле анали за эти х пр изнаков у ^ да стся с интез иро вать правила, кото ^ рые по зво лили бы оцениват ь этапы поиска : э тап спу ^ ска, к ^ огда с импле кс дого няет — 181 —

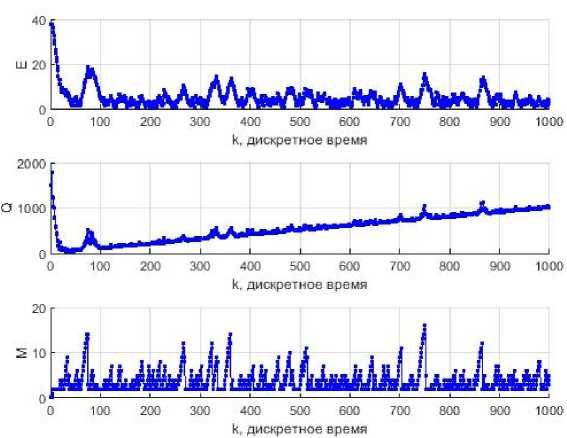
Рис. 7. Характеристики процесса поиска (большой размер ребра симплекса, 1000 шагов)

Fig. 7. Characteristics of the search process (big size of the edge of the simplex, 1000 steps)

экстремум, и этап отсл еживания, к огда симпл екс дв игается в око^ло экст рема ль ной обл асти. Для каждого из этап ов н еобх одима с воя страт егия уп равления р азмером симпл екс а.

На этапе спуска необходи мо увеличивать размер симплекса до м аксим ально до пуст имого с целью наискоре йшего достижения зоны оп тимума .

Во вре ^{^} мя отсл ежив ания необ ^{^} ходимо у ^{^} меньшать ра змер ребра до тог о уров ^{^} ня, чтобы скорости движени я симплекса и экст ^{^} ремума урав ^{^} нялись. До пуска ется менят ь ра ^{^} змер реб ^{^} ра во время отслежив а ния для т о го, чтоб ы ско ^{^} мпенсир ова ть отста вание, вызв анн ое по ^{^} м ехами и _^ ли некорре ^ ктной оце нкой скорос _^ ти др ейф а .

Рассмо трим подробнее особенности поведения Q . Имеет смысл подвергнуть анализу не только и сходную х арактер ис тику, но и не которые произв одные, котор ые м ожно получить на ее основе.

Для удобства анализа и возможного по следующего п римен ения эти хар актеристики следует пред став ить в сглаж енном вид е, н апример , испол ьзовав скольз^{^}ящ ее ср еднее. У^{^}слови м ся, что дл я расчет а ск^{^}ол ьзящ его сре дн е го б_^у^{^}де т п рим еня тьс_^я окно г_^л убино й , равной N шаг ам п о -иска. На этапе поиска до ша га N будет и спользов аться ок но с глу биной, равной текущему ша^гу. Скольз я щее среднее на каждом шаге k для Q рассчитывают следующим образом:

Q(k)=1⋅∑k Q(i).(9)

N i = k - N + 1

В качестве одной из пр оизводны х хара кте^ристик можн о рассмотреть р азност и первого и второго порядков пол ученног о ряда зна_^чений Q ( k ) :

ΔQ (k) = Q(k) - Q(k - 1),(10)

Δ2Q(k ) = ∆Q(k) - ∆Q(k - 1).(11)

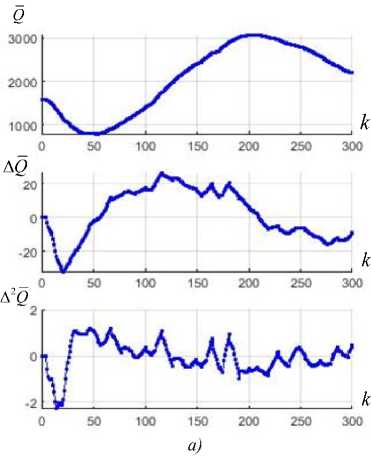
Рис. 8 . Х арактеристи ки процесс а поиск а с разным реб ^{^} ром симп лекса: а – L = 1; б – L = 4 ^,        ....

F ^{^} ig . 8 . Charac te _^ ris ti cs of th _^ e searc _^ h p roces s with a di ffer ^{^} ent e dge of t ^{^} he s imp lex: а – L = 1; б – L = 4

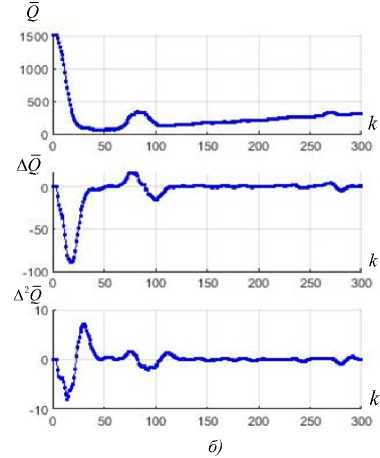
Характеристики Q ( к) . A Q ( к) и А² У ( к ) изображен ы1 на ри с. 8. П араметры модели и время моделировани я прежние. Эксперимен ты1 проведены с малыхм и большим размерами ре бра симплекса.

Н а р ис. 8 а из ображены хар ак_^тер ис тики п оис к а с бол ьшим реб_^ром симплекса. На разных ^этапах поиска ^х ар ^акт ер зависимой ^е Й ^А Q и . V Q ^отли чается.

Н ^а этапе спуска происходит И ^{адение значени} й Q - симплекс движется по ^{направлени} ю к эк^с тр е му му. А т а к к а к Δ Q и Δ ² Q мож н о счи т а^т ь соо тве т с твен но скор ос тью и у^ скорением изменения характеристики Q , то их вид будет это отражать.

^{На эта} п ^{е отслеж}Ив^{ания А} Q ^{и А} 2 Q ^{перестают резко изменятьс} я. ^{Допускаем} , ч ^{то на} этом этапе симплекс следует за экстремумом с близкой последнему скоростью, значит, значен ия Δ Q можно расценивать как оценк у скор ости вертикального дрейфа. А так как в данном эксперименте скор ость вертикального дрейф) а постоянна, то таким же б) удет и характер) ^А(^. _

Зави с имос ть Δ ² Q н а э т ап е отс л е ж и ва н и я пр ин имает б лизкие к нул евым з начения ввиду того, что колебания /А Q минимальны.

Пр им ерн о н а 75 -м шаге по и ска н а б л юдае тся р езкий вс пле ск на в сех характе ристика х – это следствие локализации симплекса в некоторой области.

На р ис . 8 б изображены хара кте рист ик и поиска с малым ре бром симплекса. В отличие от п ре дыд у щ его эк^{^}сперим ента зде сь не н а бл юда ется п ри знак^{^}ов эт апа о тслежи вания: нет по-стоян ства х ара кт е ристи к Δ Q и Δ ² Q . П^{^}р и малом шаге симплекс не м ожет достичь экстремума ⁽ _{С1 |}. р.с, ³⁾ .

Дополнительно можно рассмотреть другие характеристики поиска: разность усредненного знач ения Q на ш аге k и мини мального Q за в сю пред ыстор и ю поиска

A™Q( k)=Q(k)-min(Q), а также конечную разность, полученную на основе (13) , -        --

^ Q(k)=4-Q (k) -4 Q( k-1).

Характеристик и Q ( k ) , A min Q ( к ) и A min Q ( к) изображены на рис. 9. Параметры моде ли и время мод ели рода™ прежн№. Эксперименты продедены с малым и большим размера ми ребра симплекса.

.

Н а ри с . 9 а изображ ены ха_^ракт ери с тики пои с к а с бол ьш им р ебр ом с и м пл екса. На э тапе сп у-ска, в отличие от A Q и A 2 Q , по лученны1х в предыдущем эксперименте (рис. 8 а ), зависимости A min Q и A mn Q при ним а ют нулевые значения. На этапе отслеживания A mn Q ( к ) начинает- расти с ^некотор ой п ^остоян ной ^скор остью ^{- с} вязь ^с И^осто ян ^{ством скор} о- т и в ^{ертикальн} ого ^дре й<фа. ^Ха ра кт е ристи к а Δ ² _m ^{^} _i ^{^} _n Q ( k ) на эт о м этап е н ачин а е т при ни м ать некот о ^{^} р о е, б^{^}лизкое к постоянному, ^значен не.

На 75-м ш а г е п о ис к а так ж е на блю^д ается р езк ий в сп ле ск – след ствие закручива ния си м -илекса.

На этапе с пуска A min -) и A mn Q (к') принимают нулевые значения. Это объясняется тем, ч то Δ min Q ( k ) р а ссч ит ыв а е т ся относите л ь но ми ни ма_^л ь но го з н а ч ени я Q за в сю предыс т о ^ рию по-ис к а, и, если учитывать, что симплекс с каждым ша г о м продвигается в направлении экстремума, л юбое новое з на ч ение Q буд ет минимальным.

На рис. 9 б из ображ ^{^} ен ы хар актеристик и поиск а с малы м р ебром симплекса. В отличи е от п редыдущ его эксп е р и м ента по ви ду хара к те р ист ик нель з я увид ет ь призн аков э т апа отсл еж ива ни я : Δ _min Q ( k ) и Δ ² _min Q ( k ) н е имеют пос т о я нног о х ара ктера и зм ене ни я .

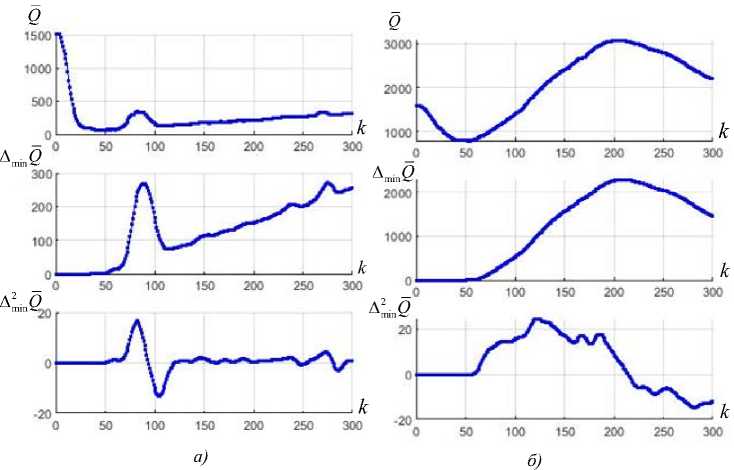
Рис. 9. Характеристики процесса поиска с разным реб^{^} ром симплекса: а – L = 4; б – L = 1

Fig. 9. Chara ct eristics of the sea^{^}rch proces s with a d ifferent e dge of t^{^}he simplex: а – L = 4; б – L = 1

Т _^ абл иц а 1. П р и знак и эт ап ов п ои ска

Table 1. Si gns o f th e se arch st a ges

Харак теристика	Ма лое ре бро симпл екса		Боль шое ребро симплекса
	Спуск	Отслежи ва^ние	Спуск	От слеживание
a Q	<0, ■' con st	Нет данны х	<0, Т const	≥0, = const
A2 Q	Т coni st	Нет данных	Т const	≈0, = const
Amm Q	0, = con st	Н ^ ет да ^ нных	≈0 , = const	≥0
a;L Q	(). = con st	Нет да нных	≈0 , = const	≠ const

Таб^ли ца 2. П^ рав и ла о це н к и эта па п ои ск а Tab le 2. Estimati^on ru les of t^he s ea^rch sta ges

Уса о1вия	Э тап работы
∆ Q ≠ const &  ∆ Q = const &  ∆ Q ≈ 0 min                    min	Спуск
∆ Q = const &  ∆ min Q ≥ 0 & ∆ 2min Q ≠ const mn         mn	Отслеж ивание

Так как симпле кс с м алым р е бр ом не им еет возможн ости достичь об ласти д рейфующего экст рем ума , то в э том с л учае э та па отсл ежи ван ия ц ели не будет как такового. На рис. 4, 8 а мож но з аметить , ч то спуск ч е ре ^ дуется с отста ванием от цели.

Оцениваю)щие правила

П олучен ную в ходе анал иза ин форма цию с ведем в таблицу пр изнаков (табл. 1).

Н а основе части соответствий признаков определенных этапов поиска в табл. 2 синтезируем п равила , котор ые позволя т п роизв ес т и оцен ку этапа поиска.

Полу чая информацию о текущем в э тапе, можно выбирать определенную стратегию поиска для достижения максимальной эффективности р аботы.

Заключение

В данной статье рассмотрен метод оценки этапа работы симплексного инвариантного метода.

Проведен анализ характеристик процесса поиска и отслеживания экстремума нестационарной статической модели. На основе выявленных закономерностей построены правила, при помощи которых можно определить текущий этап: поиск экстремума или его отслеживание.

Информацию о текущем этапе поиска можно применять для выбора оптимальной стратегии; например, на этапе спуска желательно использовать максимально допустимый размер ребра симплекса для быстрого достижения экстремальной области, а во время отслеживания необходимо регулировать размер ребра так, чтобы скорости движения симплекса и экстремума уравнялись.