Оценка качества передачи гармонического воздействия в многозонных преобразователях с двухтактной широтно- и частотно-широтно-импульсной модуляцией

В настоящее время в системах промышленной автоматики широкое распространение получили регулируемые силовые преобразователи с широтно-(ШИМ) и частотно-широтно-импульсной модуляцией (ЧШИМ) [1–5]. При этом, как правило, в основном используется однозонная ШИМ или ЧШИМ, когда выходные импульсы имеют фиксированное значение амплитуды [1–4].

Исследования, проведенные на кафедре электропривода ЮУрГУ (НИУ), показали перспективность многозонной ШИМ и ЧШИМ, позволяющей с высокой эффективностью решать целый комплекс технических задач по повышению метрологических и эксплуатационных характеристик импульсных преобразователей информации [5–8].

При многозонной модуляции максимальный диапазон ±А выходного сигнала преобразователя разделяется на несколько (n-е число) поддиапазонов (модуляционных зон МЗ), в пределах которых преобразование входного воздействия Х ВХ осуществляется в соответствии с заданной модуляционной характеристикой f₀ = f(Х_ВХ), где f₀ – частота выходных импульсов преобразователя [6]. Переход многозонного преобразователя (МРП) из одной модуляционной зоны в другую осуществляется, когда амплитуда входного сигнала превышает заданное для данной модуляционной зоны значение. Подобная структура МРП в целом ряде случаев позволяет при сохранении повышенных энергетических показателей и помехоустойчивости получить более широкую полосу пропускания частот по сравнению с однозонной модуляцией.

Многообразие принципов построения МРП [5–8] диктует необходимость сравнительного анализа качества преобразования на их основе динамического, в частности, гармонического сигнала, например, по критерию коэффициента гармоник выходных импульсов, чему и посвящена данная работа. Анализ проводился на базе пакета Matlab+Simulink.

Структурные схемы и принцип действия развертывающих преобразователей

Наибольшее распространение в системах автоматики получили многозонные преобразователи с широтно-импульсной (МРП-ШИМ) (рис. 1, а) [3, 4, 9] и частотно-широтно-импульсной модуляцией (МРП-ЧШИМ) (рис. 2, а; 3) [6–8].

В состав МРП-ШИМ входят генератор пилообразного напряжения (сигнала развертки) ГПН, сумматоры 2 1, 2 2, безгистерезисный релейный элемент РЭ и ключевые элементы К1 –Кn с зоной нечувствительности ± Ci. Выходной сигнал РЭ меняется дискретно в пределах - А/(р + 1) <  Y_P3 (t) <  A/(p + 1) (рис. 1, б), а ключевых элементов – в пределах 0 <  Y_K (t) <  |2A/(p + 1)| (рис. 1, в), где ±А - максимальная амплитуда выходного сигнала Y_ВЫХ (t) , p – число ключевых элементов МРП-ШИМ. В МРП-ШИМ число модуляционных зон определяется в соответствии с выражением Z = p + 1.

В дальнейшем ограничимся числом p = 2, что обеспечивает Z = 3 . В дальнейшем модуляционные зоны обозначаются как МЗ 1 , МЗ 2 , МЗ 3 .

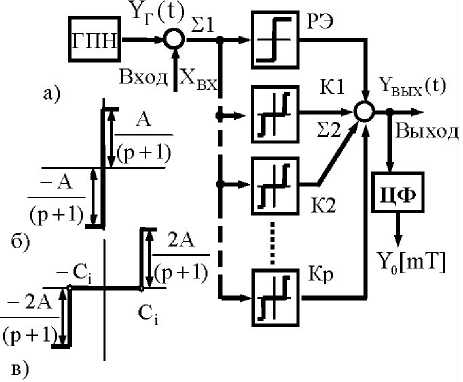
Рис. 1. Структурная схема многозонного преобразователя МРП-ШИМ

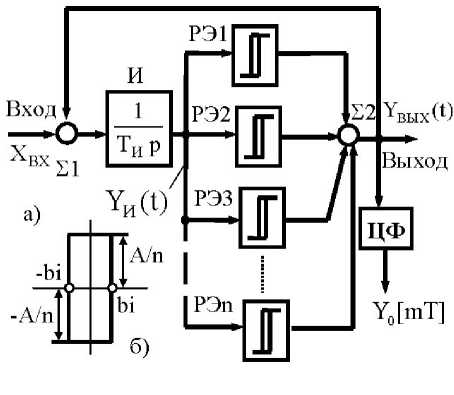
Рис. 2. Структурная схема многозонного преобразователя МРП-ЧШИМ

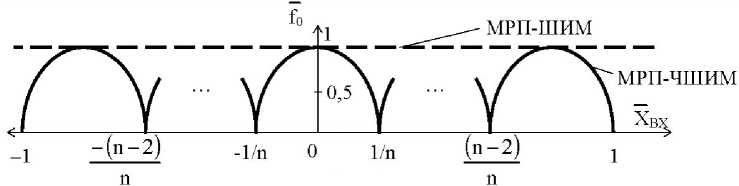
Рис. 3. Модуляционные характеристики многозонных преобразователей

В МРП-ШИМ происходит непосредственное сравнение сигнала развертки Y_Г (t) с нулевым уровнем или с некоторым заранее заданным пороговым уровнем С_i с последующей фиксацией момента времени выполнения равенства Y_r (t) = 0 или Y_Г (t)= С i путем дискретного изменения знака и/или уровня выходного сигнала Y_ВЫХ (t) МРП-ШИМ.

В дальнейшем считаем, что пороговые уровни ключевых элементов К1 – К2 удовлетворяют условию |C 1| <  |С 2| , причем |C 2| - |C 1| = А С = АГ, где А_Г – амплитуда сигнала с выхода ГПН.

Для выделения среднего значения Y₀[mT₀] из потока импульсов Y ВЫХ (t) на выходе МРП-ШИМ установлен цифровой фильтр (ЦФ), где m = 1,2,3... - целое число, соответствующее порядковому номеру интервала дискретизации Т₀ (периоду следования) выходных импульсов многозонного преобразователя.

В качестве динамического воздействия был выбран гармонический сигнал X~ (t) = А~ sin rat с нормированной амплитудой А~ = |А~/А| = 0,8, что приводит к формированию на выходе преобразователя сигнала во всех (в данном случае в трех) модуляционных зонах (рис. 4). Происходит это по причине последовательных переключений РЭ, К1, К2 в «положительное» с последующим возвратом в «отрицательное» состояния (см. рис. 4) и т. д. В результате входной гармонический сигнал X~ (t) = А~ sin rat восстанавливается на выходе МРП-ШИМ в виде «ступенчатого» сигнала Y0[mT0] . Величина «ступеньки» равна среднему значению выходных импульсов за m-й период их следования. Дискретное изменение Y0[mT0] происходит по завершению соответствующего интервала дискретизации МРП-ШИМ, когда между входным сигналом и средним значением выходных импульсов существует однозначная связь и ЦФ в состоянии вычислить постоянную составляющую выходных импульсов.

МРП-ЧШИМ представляет собой замкнутую интегрирующую автоколебательную систему (см. рис. 2, а). В ее состав входят сумматоры Σ1 и Σ2, интегратор И с передаточной характеристикой вида W(p) = , где Ти - постоянная времени ТИp И интегрирования и релейные элементы РЭ1 –РЭn с симметричными относительно «нуля» порогами переключения, удовлетворяющими условию |±bi | <|±b2| < - —< |±bn|. Здесь индекс при b соответствует порядковому номеру РЭ. Амплитуда выходных импульсов каждого из РЭi меняется в пределах YРЭi = ±A / n (рис. 2, б), где n > 3, 5, 7— -нечетное число. Максимальный выходной сигнал

Устройства аналоговой и цифровой электроники

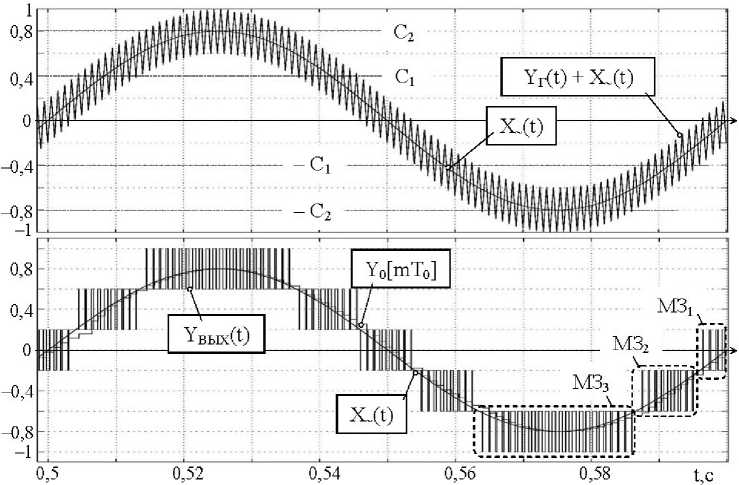
Рис. 4. Временные диаграммы сигналов МРП-ШИМ при гармоническом входном воздействии с нормированной амплитудой A _ (t) = 0,8

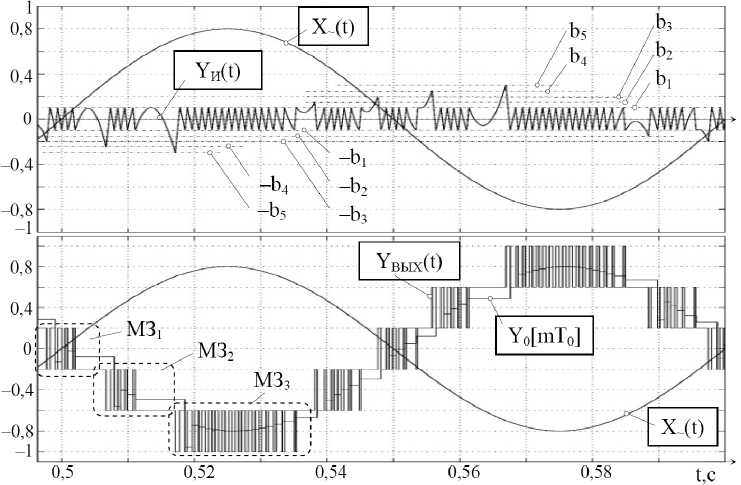
Рис. 5. Временные диаграммы сигналов МРП-ЧШИМ при гармоническом входном воздействии с амплитудой A ~ (t) = 0,8

МРП-ЧШИМ равен ±А (см. р и с . 2, б). В режиме автоколебан и й всегд а наход ит с я РЭ с ми н и ма л ьн ы м знач е н и ем п о р о г о в пе р ек л ю ч е ни я , в д анн о м сл уч ае РЭ1 . О ст а льн ы е РЭ р аб о т а ю т в с т ати ч е ск о м состоянии A/n или - A/n (см. р ис . 2, б). Ограничимся числом релейных элементов n = 5, что, в соответствии с выражением Z = (n + 1 )/ 2 = 3 , обеспечивает, как и в МРП-Ш ИМ , т р и мо д уля ци о н н ы е зоны.

При гармоническом сигнале X~ (t) = А~ sin mt на входе МРП-ЧШИМ преобразователь последо- вательно переходит из первой (МЗ1) в более старшие модуляционные зоны (МЗ2 и МЗ3), а затем обратно. Происходит это в результате последовательной с ростом амплитуды сигнала X~ (t) переориентации РЭ2, РЭ3 под действием выходного сигнала YИ (t) интегратора И (см. рис. 2). Полезная составляющая Y0[mT0 ] выходных импульсов YВЫХ(t) МРП-ЧШИМ складывается из среднего значения импульсного потока текущей модуляционной зоны и постоянной составляющей предшествующих модуляционных зон (рис. 5).

В результате координата Y0[mT0] выходного сигнала YВЫХ (t) МРП-ЧШИМ пропорциональна величине Х~ (t) (см. рис. 5) и инверсна по отношению к этому входному воздействию.

Принципиальное различие между МРП-ШИМ и МРП-ЧШИМ наглядно показывает модуляционная характеристика f₀ — f (Х _вх ), которая не зависит от входного сигнала XВХ и постоянна во всем диапазоне его изменения для МРП-ШИМ и имеет точки с f ) — 0 (частотно-нулевое сопряжение модуляционных зон) – для МРП-ЧШИМ (см. рис. 3).

Анализ проводился в среде Matlab+Simulink [11] в соответствии с выражением (1) для диапазона частот f~ ≤0,1, что соответствует реальной полосе пропускания импульсных преобразователей с ШИМ и ЧШИМ при гармоническом входном воз-

действии [12, 13]. Здесь f ~ =

- о|Хвх — 0

– нор-

Здесь Х вх — Х вх /А

входного сигнала, f0

ная частота f₀ — T_o¹

– нормированная величина

^— |^f o/ ^f o|X _BX — о| ^- нормирован^-выходных импульсов преоб-

разователя; ^fox_Bx — о ^{— Т}о - Х_ВХ — о импульсов преобразователей нии сигнала на входе.

– частота выходных

при нулевом значе-

Теоретическая часть

В соответствии с ГОСТ

13109–97 [10], каче-

ство выходного сигнала оценивают по коэффициенту гармоник KГ , определяемому по формуле

КГ —

A(1) ,

мированное значение частоты f~ гармонического входного сигнала Х~(t).

При малых значениях амплитуды A_~ (рис. 6, а) характеристики K Г = f( f_~ ) для МРП-ШИМ и МРП-ЧШИМ практически идентичны. Это является следствием того, что в данном диапазоне входного сигнала модуляционные характеристики для этих преобразователей фактически совпадают (см. рис. 3).

Когда же амплитуда динамического входного сигнала существенно возрастает (рис. 6, б), частота следования выходных импульсов в МРП-ЧШИМ «в среднем» падает, а переход из одной модуляционной зоны в другую сопровождается задержкой, обусловленной временем переключения соответствующего из релейных элементов РЭ2, РЭ3. Это приводит к тому, что величина KГ для МРП-ЧШИМ существенно возрастает. Здесь МРП-ЧШИМ проигрывает преобразователям типа МРП-ШИМ по качеству преобразования динамического сигнала.

Однако не следует забывать, что МРП-ЧШИМ является замкнутой системой с интегратором в прямом канале регулирования, что обеспечивает его высокую статическую точность и помехо-

где A(1) и A(k) – амплитуда первой и k-х гармо-

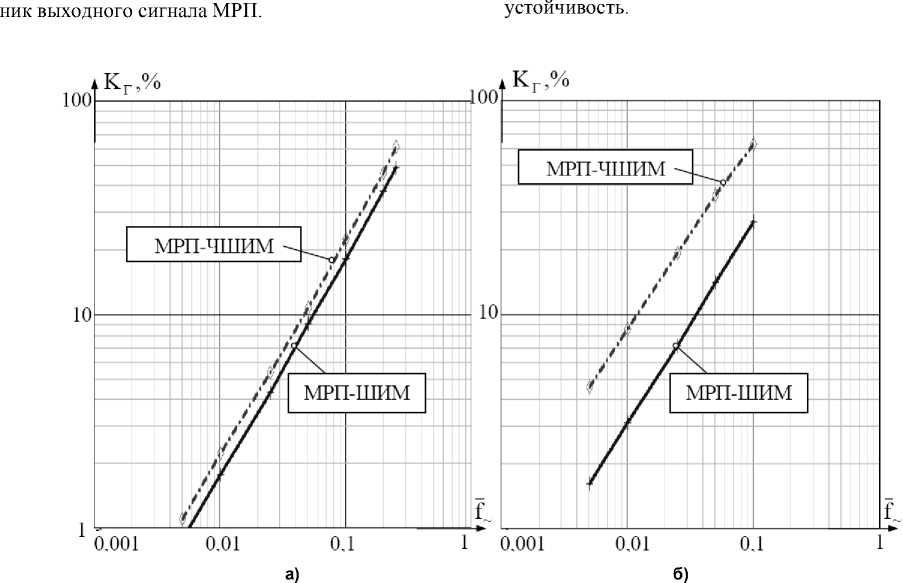
Рис. 6. График зависимости коэффициента гармоник выходного сигнала от относительной частоты гармонического входного воздействия при нормированной амплитуде гармонического

сигнала A_~ = 0,1 (а) и A_~ = 0,8 (б)

Устройства аналоговой и цифровой электроники

Выводы

• 1.    Минимальным коэффициентом гармоник K_Г во всем рабочем диапазоне частот f_~ обладает МРП-ШИМ.

• 2.    В преобразователях с ЧШИМ коэффициент гармоник K_Г больше, так как частота f₀ выходных импульсов подобных МРП снижается с ростом амплитуды гармонического сигнала. Поэтому количество отсчетов, необходимых для восстановления гармонического выходного сигнала, оказывается меньше чем в преобразователях с ШИМ, где частота f₀ остается постоянной во всем диапазоне изменения входного воздействия.

• 3.    При работе с динамическим воздействием большой амплитуды, когда оказываются задействованными все модуляционные зоны, коэффициент гармоник K_Г всех преобразователей возрастает, так как амплитуда дискретизации сигнала Y₀[mT₀] по уровню также увеличивается. При этом в МРП-ЧШИМ K_Г возрастает значительнее по сравнению с МРП-ШИМ по причине наличия в модуляционной характеристике точек частотнонулевого сопряжения модуляционных зон.