Оценка качества процессов различными методами и влияние на них вариабельности систем измерений

Для каждой группы людей понятие качества своё. Ещё сложнее это самое качество оценить и тем более измерить количественно. Но при определённых условиях для отдельных случаев это всё же возможно. Однако, не любая оценка может быть полезна, иногда она даже может быть вредна, а её результаты могут привести к ошибочным управленческим решениям. В данной статье подробно рассмотрены два подхода: традиционный, основанный на допусках, и относительно новый, основанный на функции потери качества по Тагути. Кроме того, мы обсуждаем часто используемые для оценки качества процессов индексы воспроизводимости, и влияние на них вариабельности системы наших измерений. Практическое рассмотрение всех обсуждаемых вопросов выполнено с учётом реальных данных конкретного производства.

Смелов Владимир Юрьевич,

Ахметова Е.А., Олексенко Я.Г.

«Причина, по которой люди по-разному воспринимают качество заключается в том, что каждый подходит к этому событию со своим собственным набором аналогий».

Роберт Пирсинг, «Дзен и искусство ухода за мотоциклом»

1.    ДВА ПОДХОДА К ОЦЕНКЕ КАЧЕСТВА

Оценка качества производственных процессов позволяет принимать управленческие решения о их соответствии предъявляемым требованиям, а также учитывать приемлемость соотношения затрат на обеспечение желаемого качества с ценой, которую готов платить потребитель. Если говорить о качестве продукции, например, машиностроительного производства, то тут на сегодняшний день существует два принципиально разных подхода. Первый можно назвать допусковым. Он возник довольно давно. Суть его сводится к тому, что и покупатель, и производитель прекрасно понимают, что в силу ряда причин нельзя получить множество одинаковых деталей, которые нельзя отличить друг от друга. Поэтому они договариваются о допустимых/приемлемых для потребителя отклонениях от желаемого значения. Так появляются граничные значения, а диапазон между ними называется допуском. Этот подход оказался на практике весьма эффективным, и получил широкое распространение. И как это часто бывает, то, что повсеместно применяется, стало объектом стандартизации, и появилась целая система стандартов на допуски всех возможных параметров от размеров до форм. Это позволило получить унифицированный язык взаимодействия между разработчиками, произ- водителями и потребителями. Но есть ряд нюансов. Во-первых, производитель всегда борется за расширение поля допуска, так как это даёт ему свободу с точки зрения стоимости исходных заготовок, точности и периодичности обслуживания оборудования, расходов на инструмент, оснастку, смазочно-охлаждающие жидкости, квалификации основного и вспомогательного персонала, уровня контроля и многого другого. Во-вторых, покупатель почти всегда борется за сужение поля допуска, так как ему нужны гарантии и уверенность в том, что у него не появятся проблемы в самый ответственный момент, например, на стадии сборки или испытания, а то и эксплуатации конечного изделия. В-третьих, величина поля допуска - квалитет, прямо привязана к затратам так, что чем уже допуск, тем выше затраты на его обеспечение, в том числе и за счёт отбраковки негодных деталей. И, в-четвёртых, но не в последнюю очередь, договорённость о допусках привела многих к выводу о том, что экономические потери из-за низкого качества продукции возникают только в том случае, когда значение контролируемого параметра оказывается за пределами поля допуска. Т.е., по сути: если изделия в допуске, то потери равны нулю, а за пределами поля допуска они фиксированные.

Второй подход - довольно молод, и не успел ещё получить столь широкого распространения, как допусковый. Этот подход предложен японским учёным Генити Тагути во второй половине прошлого столетия [9]. Суть его в том, что любое отклонение от целевого значения ведёт к потерям качества, причём эти потери растут пропорционально квадрату отклонения. Парабола, описывающая функцию потерь по Тагути, пересекается с точкой фиксированного уровня потерь на границе поля допуска. Формула выглядит следующим образом [1]:

1л. = ;_Л-".- , (1)

где x - измеренное значение показателя качества;

T - целевое значение показателя качества;

с - коэффициент масштаба, подбираемый в зависимости от значения фиксированного уровня потерь на границе поля допуска и используемой денежной единицы для её оценки. По сути, он представляет собой стоимость квадрата отклонения фактического значения от целевого;

L(x) - значение функции потерь Тагути в точке x .

При этом важно отметить, что в тех случаях, когда потери для неисправимого и исправимого брака разные, коэффициент масштаба с следует для каждой «стороны» вычислить отдельно. Дальнейшее обсуждение мы будем вести для случая, когда потери при выходе за границы по допусковому подходу равны ???. Кроме того, следует понимать, что точно вычислить уровень потерь в реальности не представляется возможным, так как бухгалтерский подход не учитывает множество факторов, которые невозможно определить, а тем более оценить количественно. Формула (1) представляет собой «наиболее естественную и простую математическую функцию, пригодную для представления основных особенностей функции потерь Тагути» [1]. И здесь важно отметить, что функция потерь Тагути служит моделью, а не истинной функцией потерь, но эта модель гораздо ближе к фактическому состоянию дел, чем допусковый подход.

Из формулы (1) понятно, что при совпадении фактического значения с целевым потери в любых денежных единицах будут нулевыми, а затраты на изготовление будут содержать только стоимость изготовления данной детали без добавления потерь на брак, исправление и гарантийное обслуживание. Но откуда же берутся эти потери? Если нет претензий и формальных оснований говорить о каких-либо нарушениях, то и экономических затрат быть не должно. Но, во-первых, если производится бракованная продукция, отгрузка которой исключается контролем, то затраты на изготовление этой бракованной детали и на её выявление при контроле включаются в себестоимость. Во-вторых, если брак исправимый, то его исправление включается в себестоимость. В-третьих, если поставщик несёт гарантийные обязательства, то стоимость гарантии также включается в себестоимость. Гарантия вопреки иллюзиям не бесплатна. За всё это и многое другое платит потребитель. Другого источника, за редким исключением, у производителя нет. И так как почти всегда отдельно взятые детали входят в состав сложных изделий, а то и очень сложных систем, то выход из строя даже самой дешёвой детали может привести к дорогостоящему ремонту. Автолюбители с опытом могут рассказать немало примеров о том, как повреждение копеечного уплотнителя привело к дорогостоящему ремонту двигателя или трансмиссии.

• 2.    КОНТРОЛЬНЫЕ КАРТЫ ШУХАРТА И ИНДЕКСЫ ВОСПРОИЗВОДИМОСТИ ПРОЦЕССОВ

Главная причина того, что нельзя получить множество абсолютно одинаковых значений на выходе любого процесса, это вариабельность. Вариабельность нельзя исключить, хотя ею можно и нужно управлять. Снижение вариабельности - самый эффективный способ обеспечения выпуска продукции стабильного качества. Инструментом оценки вариабельности процессов служат контрольные карты Шухарта [см. например, 6], а мерой - стандартное отклонение или дисперсия. Контрольная карта Шухарта (ККШ)

представляет собой карту хода процесса с нанесёнными на неё естественными границами и средней линией (могут быть использованы и другие показатели, свёртывающие совокупность данных в одно значение, например, медиана). При этом, если процесс стабилен, то при его сохранении в таком состоянии можно уверенно утверждать, что любой следующий результат будет в диапазоне границ процесса. При этом верхняя граница процесса, как правило, расположены на расстоянии плюс 3σ относи- тельно среднего значения, а нижняя – на расстоянии минус 3σ. Таким образом получается, что диапазон между границами процесса, часто называемый «голосом процесса», равен шести стандартным отклонениям (СО), то есть 6σ.

В то же время согласно допусковому подходу, мы имеем границы допуска, которые в свою очередь среди специалистов по статистическому управлению качеством (SPC) принято называть «голосом потребителя». И, есте- ственно, взаимное расположение границ поля допуска и границ ККШ представляет огромный интерес с точки зрения управления качеством. Так появились индексы воспроизводимости процессов (ИВП).

Первое знакомство с ИВП, как правило, на- чинается с индекса, обозначаемого Cp. Данный индекс определяется по формуле [4]:

, _ ЕГД-НГД р б " ^,

где ВГД и НГД – верхняя и нижняя границы допуска, соответственно, а о – это оценка внутригруппового СО, определяемая по формуле [4]:

_ К а = — ,               (3)

где Д – средний внутригрупповой размах, и d₂ – зависящая от объёма группы константа для оценки СО.

Индекс С_р применяют в тех случаях, когда процесс настроен точно на середину поля допуска. Если настройка процесса отклоняется от середины, нужно использовать другой индекс – C_pk . Его находят по формуле:

/ ЕГД-х

Срк ^{— т}*-^п } х-НГД ,          (4)

V 38

где X – это, как обычно, среднее арифметическое по нашим данным.

Вот как выглядят правила оценки индекса С_р , приведённые в [5], и применяемые в нашей стране во многих отраслях:

1,33 ≤ C p        вполне удовлетворительно;

1,00 ≤ Cp < 1,33 адекватно;

C_p< 1,00        неадекватно » .

Указанные выше границы при условии нормальности распределения параметров соответ- ствуют уровню дефектности 66 ppm для Cp = 1,33 и 2700 ppm для Сp = 1,001.

Если величину стандартного отклонения в формулах (2) и (4) вычислять не по формуле

(3), а по той формуле, какая приводится во всех учебниках по статистике, и какая зашита, на- пример, в пакете Microsoft Excel

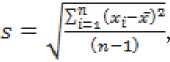
то вместо индексов C_p и C_pk получаем другую пару ИВП – P_p и P_pk . В стандарте [7] данные индексы названы индексами пригодности процесса. На первый взгляд индексы C_p ( С_pk ) и P_p ( P_pk ) друг от друга не отличаются. Так оно и происходит для стабильных процессов², т.к. в этом случае разные способы расчёта стандартного отклонения дают одинаковые результаты. Но в случае, когда процесс нестабилен (или когда он не случаен – см. ссылку в примечании 2), формулы (3) и (5) приводят к разным значениям, причём почти всегда д <  s . В итоге стандарты рекомендуют применять индексы C_p и C_pk для стабильных процессов и коротких промежутков времени, а индексы P_p и P_pk – для нестабильных процессов и длительных времён.

Этими четырьмя ИВП большинство предприятий ограничивается, так как большего никто и не требует. На самом деле, кроме указанных, имеется великое множество других ИВП, и число их продолжает расти. В этом можно убедиться, например, ознакомившись с книгой [8], которая не переведена на русский язык.

Но среди множества ИВП, которые не получили широкого распространения, есть такие, какие тесно связаны с идеей функции потери качества Г. Тагути [9]. Эти индексы с нашей точки зрения более информативны, по крайне мере в тех случаях, когда процесс имеет заданную цель, важную для потребителя. Если такая ситуация имеет место, то интуитивно кажется, что лучше применять именно эти ИВП.

Вот как определяются ИВП по Тагути [7]:

,  _ ЕГД-НГД

■рТ 61Рг ,

где

а^ = а^я+ ^- Т)^г .

В формуле (7) через μ обозначено среднее генеральной совокупности (т.е. то, чего мы никогда не знаем, и что мы на практике заменяем на X), через T (Target) – целевое значение процесса, а через σ – стандартное отклонение генеральной совокупности, которое заменяется на оценки по формуле (3) или (5). Так как теперь у нас кроме среднего появилось ещё и целевое значение, то возникает много вариантов построения индексов. Самый простой среди них в книге [8] назван модифицированным индексом или C : pm тш{ЕГД—Т,Т—НГД] .               (8)

Далее можно ввести аналог индексу C_pk , использующий – C_pTk (см. главу 3 в книге [8]). А если учесть, что в формулу (7) можно подставлять стандартные отклонения, рассчитанные разными способами (формулы (3) и (5)), то масштаб бедствия становится очевидным.

3.    РАБОТА С ИНДЕКСАМИ ТАГУТИ

Как уже было отмечено выше, добавляя к обычным ИВП целевое значение, можно построить много различных индексов, анализ которых представляет собой, с одной стороны, существенные технические трудности (даже в условиях нормальности), а, с другой стороны, это практически неисследованная область. Так как наша работа имеет сугубо практическую ориентацию, мы рассмотрим только один, причём очевидный аспект влияния целевого показателя на ИВП, а именно, влияние изменения величины стандартного отклонения в соответствии с формулой (7). При этом мы не будем анализировать те аспекты проблемы, какие интересны профессиональным статистикам, а остановимся на важных для практики результатах: как изменится расчётная доля брака, если в стандартном отклонении будет учтено смещение среднего процесса по отношению к его цели (Т). Если принять, что процесс стабилен и нормальность параметров имеет место, то доля брака (ДБ) при заданных нижней границе допуска (НГД) и верхней границе допуска (ВГД) в книге [6]3 описывается уравнением (9):

ДБ = 2 – Ф(3·CPL) – Ф(3·CPU),       (9)

где греческая буква Ф как обычно обозначает кумулятивную функцию нормального закона, а индексы CPL и CPU по определению равны

,              (10.1)

• 3    g-

• .               (10.2)

• 3    CF

Из уравнения (6) имее м:

,            (11)

\       ff0

где мы вместо μ написали , так как в реальной жизни никакого истинного среднего генеральной совокупности нет, а есть только среднее значение по той или иной выборке. Подставляя (11) в (9), получаем

, (12)

• ^{м v v}           \г₀^Т+5^{7 V}ff₀vTTJ⁷ ’

где – это обычное стандартное отклонение, определяемое формулой (3) или (5), а буквой z мы обозначили величину , т.е. величину

TD отклонения среднего от цели в единицах стандартного отклонения (нормированное на сигму отклонение среднего от цели). На рисунке 1 показано, как растёт отношение величины ДБ(z) к той ДБ, какая была бы без задания целевого значения – ДБ0.

Из рисунка 1 очевидно, что только за счёт роста величины стандар тного отклонения ДБ

ДБ(2)/ДБ0

ДБ(2)/ДБ0

—•— Cpk=l —•— Cpk=0,9 • Cpk=0,8

—e— Cpk=0,7 —•— Cpk=0,5

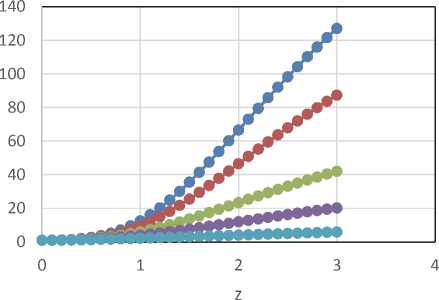
Рис. 1 – Зависимость отношения ДБ(z) к ДБ₀ от нормированного отклонения среднего от цели процесса. Справа показана та часть кривых, которая плохо различима на левом рисунке

• С p k= 1,0 • Cp k=0,9 • Cp k=0,8

—•— Cpk=0,7 —e— Cpk=0,5

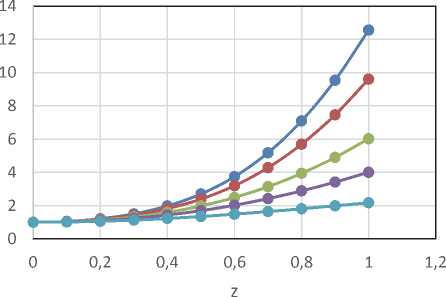
резко растёт, причём влияние отклонения от цели увеличивается при росте значений ИВП. Это вполне понятно: чем выше значение индекса, тем у́же колокол распределения, тем сильнее влияние роста значений сигмы из-за отклонения от цели. Стоит подчеркнуть, что отношение ДБ(z) к ДБ0 – это не оценка реального брака, а просто способ оценивания степени влияния отклонения от цели на качество процесса. Вопрос о том, как пересчитать эту величину в потери по Тагути, требует, прежде всего, уточнения функции потерь в соответствии с реальными потерями производства.

4.    ВЛИЯНИЕ КЛАССА СИСТЕМЫ ИЗМЕРЕНИЙ НА ИВП ПО ТАГУТИ

В работе [2] было предложено использовать подход Д. Уилера [3] по классификации систем измерения, но с другими границами, какие больше соответствуют мировой метрологической практике. Из определения внутриклассового коэффициента корреляции (ICC)

сразу следует, что

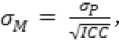
где – это значение стандартного отклонения, какое мы получаем по нашим данным, а – это значение стандартного отклонения собственно изделий, то есть без учёта вариабельности системы измерений. Подставляя (14) в (7) получаем

. ^.

А подставив (15) в (6), получаем:

_ вгд-нгд

.

Заменив σ в (10.1) и (10.2) на (14) и подставляя в формулу (9), получим:

J1CC +^^ J/cc +^^

ДБТ – доля брака для ИВП по Тагути с учётом вариабельности системы измерения.

ДБ_Т0 – доля брака для ИВП по Тагути без учёта вариабельности системы измерения, то есть при ICC = 1 .

Таким образом влияние вариабельности системы измерения на оценочную долю брака

ДБт можно оценить соотношением . Зависи-

ДБю

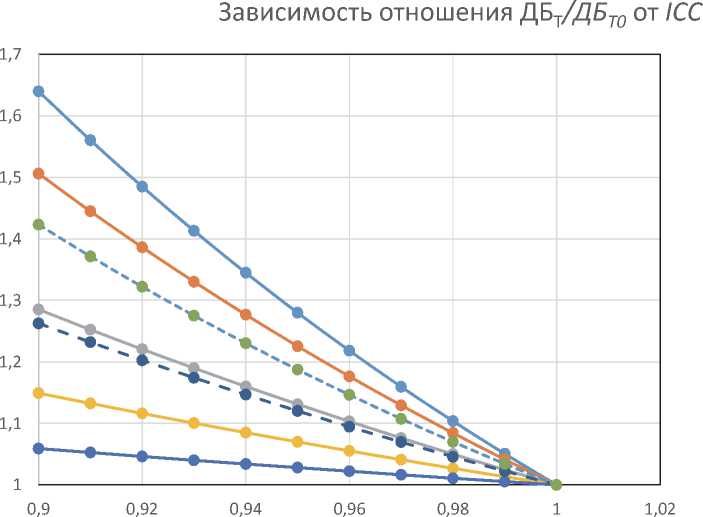
ДБт мость от ICC приведена на рисунке 2.

ДБТо

Из рисунка 2 следует, что при C_pT = 1,0 максимальное влияние вариабельности системы измерений наблюдается при настройке процесса на целевое значение ( T ). При этом для систем измерений I класса ( ICC ≥ 0,99 ) при значении индекса C_pT = 1,0 рост брака из-за системы измерений равен 5 % , для систем II класса ( 0,99 >

—е—срт=1,о х-т=о

—•—СрТ=1,0 Х-Т=0,33о

—•—СрТ=1,0 Х-Т=0,67а

—•— СрТ=1,0 Х-Т=1,0а

—•—СрТ=1,0 Х-Т=1,5а

- • - СрТ=1,33 Х-Т=1,0а

—•— СрТ=1,67 Х-Т=1,0а

ICC

Рис. 2 – Зависимость отношения доли брака с учётом вариабельности системы измерений к доле брака без учёта вариабельности системы измерений

ICC ≥ 0,96 ) этот рост составит 21,8 % при ICC = 0,96 , для систем III класса при ICC = 0,90 – 63,9 % . Если индекс C_pT будет равен не 1,0 , а, например, 1,33 , то максимальное увеличение ДБ будет 26 % (кривая С_рT = 1,33 , х-Т = 1,0 σ на рисунке 2). При этом кривые для С_рT = 1,33 , х-Т= 1,0 σ и С рT = 1,0 , х-Т= 0,33 σ близки друг к другу. Если C_pT = 1,67 , то рост величины ДБ будет более 42 % (кривая С_рT = 1,67,х-Т= 1,0 σ на рисунке 2). Как и можно было ожидать, влияние системы измерений проявляется тем больше, чем больше значение индекса C_pT , а влияние вариабельности системы измерений тем выше, чем выше требования к процессу. Следовательно близость настройки процесса к целевому значению и рост ИВП по Тагути ужесточают требования при выборе системы измерений с целью уменьшения вероятности принятия неверного управленческого решения.

• 5.    СРАВНИТЕЛЬНЫЙ АНАЛИЗ ОЦЕНКИ ЗАТРАТ НА КАЧЕСТВО С УЧЁТОМ ВЛИЯНИЯ ВАРИАБЕЛЬНОСТИ СИСТЕМ ИЗМЕРЕНИЙ В УСЛОВИЯХ РЕАЛЬНОГО ПРОИЗВОДСТВА

Теперь рассмотрим данные, полученные в условиях реального производства, и сравним оценку финансовых потерь из-за несоответствия продукции требованиям по качеству с точки зрения двух разных подходов. Эти потери принято называть затратами на качество, хотя, справедливости ради стоит отметить, что авторам не встречались российские предприятия, которые учитывали бы эти затраты с точки зрения подхода Тагути.

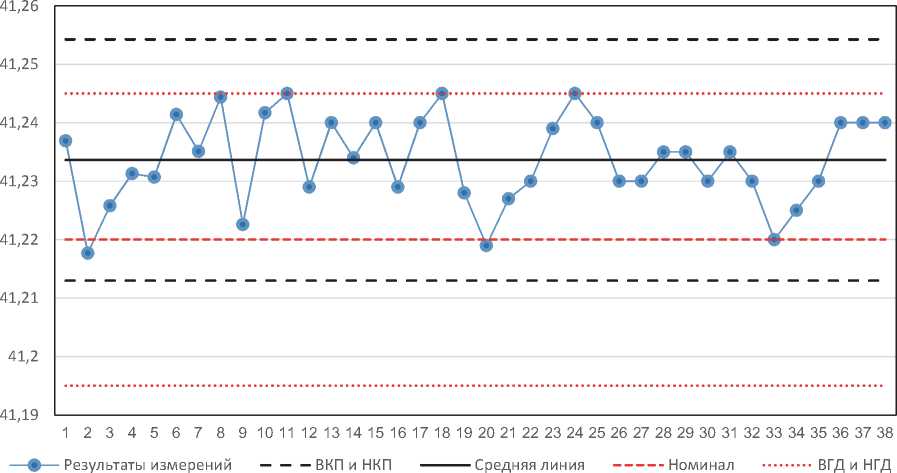
На рисунках 3 и 4 представлены контрольные карты индивидуальных значений с границами допуска (и контрольные карты скользящих размахов под ними) по результатам измерений внешних диаметров двух деталей «палец» и «втулка», которые входят в состав гусеничной цепи, производимой ООО ПК «ЧАЗ». Кроме деталей «палец» и «втулка» гусеничная цепь состоит из двух симметричных деталей «звеньев», в ответные отверстия которых впрессовываются «втулка» и «палец», а также комплекта уплотнителей и заглушек. Установив на гусеничную цепь детали «башмак» и закрепив их четырьмя парами «болт-гайка», получаем гусеницу для промышленных тракторов и экскаваторов. При этом в качестве запчастей к ходовым системам промышленных тракторов покупаются как отдельно гусеничные цепи, так и целиком гусеницы. Мы будем рассматривать только гусеничную цепь, чтобы пример не стал слишком громоздким и сложным. Кроме того, на промышленный трактор, конечно же, устанавливается два комплекта гусениц, но опять же с точки зрения целей данной работы достаточно рассмотреть один комплект. В каждую гусеничную цепь входят по 38 деталей «палец», «втулка» и пар симметричных «звеньев», а также комплектов уплотнителей и заглушек.

Важное техническое замечание. Применяемая система допусков и посадок далеко не всегда в качестве номинала указывает целевое значение. Дело тут в том, что в качестве номинального значения часто используются одни и те же значения как для отверстий, так и для валов, а взаимным расположением полей допусков обеспечивается желаемая посадка: с зазором, переходная или в натяг. Так и у втулки 070,00 мм сопрягается с отверстием звена 070,00 мм и обеспечивается гарантированная посадка в натяг от 0,23 до 0,40 мм. Потому для пальца номинал не может быть целевым значением, как и для ответного отверстия. Так как в данном случае информации о том, какое значение следует считать целевым, у нас отсутствует, в качестве такового выбраны середины поля допуска. А вот что касается пальца и его ответного отверстия в звене, то тут выбраны номинальные значения таким образом, что границы полей допуска расположены симметрично – Ø41,22±0,025 мм и Ø40,87±0,05 мм соответственно, что даёт гарантированную посадку от 0,275 до 0,425 мм. Кроме этого, следует отметить, что на рисунках 3 и 4 представлены результаты измерений диаметров пальцев и втулок с одной стороны, результаты измерений с другой стороны принципиально не отличаются и не будут приводиться с целью экономии места. Все измерения проводились на трёхкоординатной измерительной машине IMPACT 600.

Рисунки 3 и 4 позволяют нам понять, что оборудование настроено на верхнюю половину поля допуска, процессы стабильны со статистической точки зрения, а бракованной продукции, согласно допусковому подходу, нет. Соответственно, и потери в таком случае ожидаемые потери будут приравнены нулю. Но на самом деле мы видим (обе контрольные карты индивидуальных значений) что верхние контрольные пределы (ВКП) находятся выше верхних границ допуска (ВГД), а ряд значений расположены либо очень близко к ВГД, либо на ней (такая продукция признаётся годной). Очевидно, что процесс настроен таким образом, чтобы бракованная продукция в случае возникновения была исправимой, то есть можно было снять слой металла за пределами ВГД и обеспечить плановую выработку, а вместе с ней и премию оператору. При этом стоимость доработки именно на этих диаметрах до нанесения покрытия и термообработки менее 5 %, что с учётом того, что примерно половина деталей может выйти за ВГД, снижается ещё более, чем в два раза.

Теперь рассчитаем ИВП C_p и C_pk , а также ИВП по Тагути (см. таблицу 1), по которой мы можем

0,0300

0,0250

0,0200

0,0150

0,0100

0,0050

0,0000

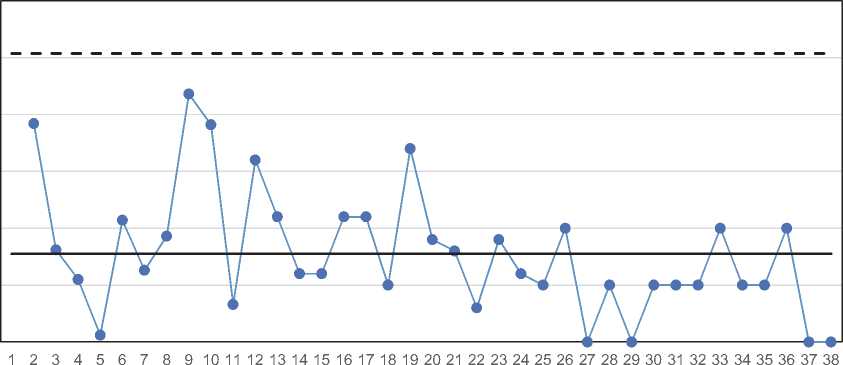
Рис. 3 – Контрольные карты индивидуальных значений с нанесёнными на неё границами поля допуска и номинальным значением (сверху) и скользящих размахов (снизу) для диаметра детали палец (Ø41,22±0,025 мм)

сделать вывод, что действительно воспроизводимость статистически стабильных процессов на вполне приемлемом уровне, однако настройка смещена в сторону ВГД. ИВП по Тагути говорят о том, что настройки процессов далеки от середин поля допуска, и что потери будут существенными.

Теперь рассчитаем потери для наших деталей согласно формуле (1), для которой сначала следует определить значения коэффициента c. Так как выявление брака на этапе сборки исключает возможность доработки этих деталей (они уже прошли термообработку, и на них нанесено покрытие), то на этой стадии брак может быть только окончательным. Полная себестоимость изготовления одной детали «палец» составляет 1 003,11 руб./шт., для детали «втулка» – 1 868,74 руб./шт. Таким образом для формула (1) для деталей «палец» и «втулка» будет выглядеть следующим образом:

L™qGO = 1 604 976 (x- 41,220)2

(для детали «палец»),

^to = 2 989 984 (x- 70,375)2

(для детали «втулка»).

70,42

70,41

70,4

70,39

70,38

70,37

70,36

70,35

70,34

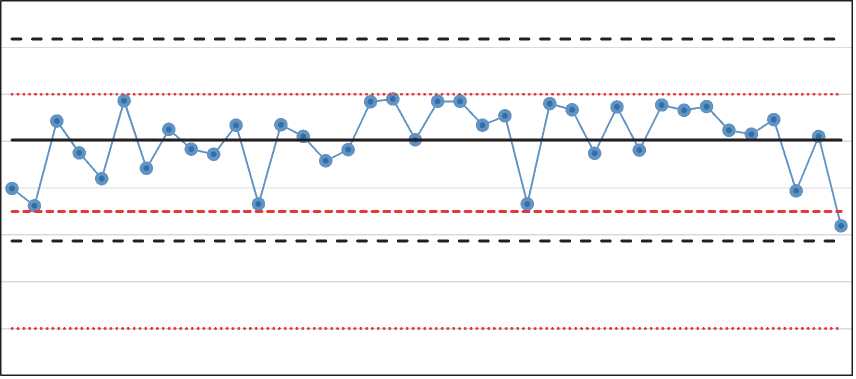
—• Результаты измерений---ВКП и НКП -----Средняя линия -----Середина допуска .........ВГД и НГД

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38

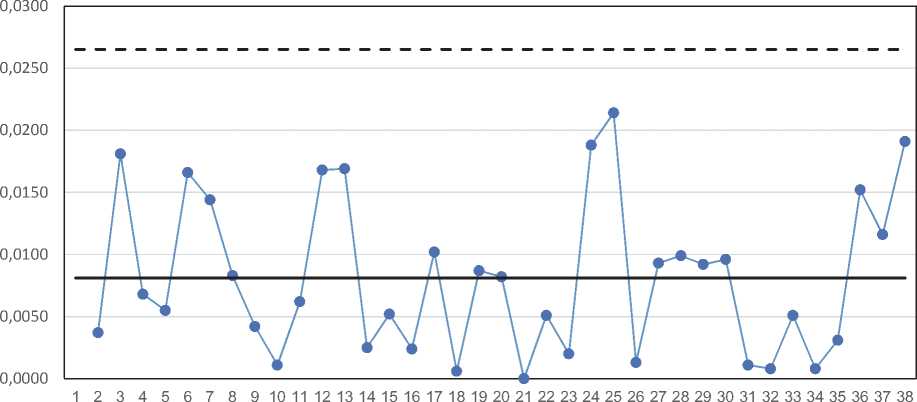
Рис. 4 – Контрольные карты индивидуальных значений с нанесёнными на неё границами поля допуска и значением середины поля допуска (сверху) и скользящих размахов (снизу) для диаметра детали палец (           мм)

Эти выражения позволяют определить потери как для каждой отдельной детали, так и для всех деталей, которые были измерены. Для «пальца» максимальное значение потерь равно 1003,11 руб. (для изделий, результат измерения которых равен значению ВГД), а минимальное – 0,00 руб. (для изделий, результат измерения которых совпадает с номиналом). Для «втулки» 1722,23 руб. и 4,31 руб. соответственно. Суммарные потери согласно Тагути для всей гусеничной цепи составят 14 659,37 руб. для «пальцев» и 32 510,93 руб. для «втулок», что составляет 38,46 % и 45,78 % соответ- ственно от полной стоимости изготовления всей гусеничной цепи целиком. Так как стоимость гусеничной цепи составляет 177 752,34 руб., то текущий уровень потерь составляет 26,54 %. При этом следует понимать, что это совокупные потери, которые могут быть понесены дополнительно в процессе эксплуатации конечного изделия.

Далее следует рассмотреть связь между функцией потерь Тагути и ИВП. Для этого воспользуемся расчётами из [1, стр. 172], где средние потери по Тагути равны:

, (18)

Таблица 1 – Значения ИВП для изделий «палец» и «втулка»

	C p	C pk	C pT	C pTk
041,22±О,О25 мм	1,212	0,552	0,546	0,249
070,00 ^°^ мм	1,160	0,453	0,495	0,193

+ (40,8662 — 40,87)2} = 4271,85 (руб.)

и

соответственно, сумма потерь, которую обозначим S, равна произведению (18) на количество деталей в выборке n :

. (19)

Так как выражение в фигурных скобках представляет собой ни что иное, как (см. формулу (7)), то можно выразить зависимость суммарных потерь от ИВП по Тагути:

_ ,вгд-нгдч2

. (20)

Таким образом, что вполне очевидно, мы видим, что суммарные потери обратно пропорциональны квадрату ИВП по Тагути. Допуско-вый подход не только не позволяет определить уровень потерь для изделий, которые соответствуют требованиям допуска, но и не имеют явной связи со значениями ИВП.

Следует отметить, что вычисления средних или суммарных потерь, как и вообще любые выводы и управленческие решения применительно к процессам, имеют смысл только для стабильных со статистической точки зрения систем. Кроме этого, формула (19) позволяет довольно легко определить оценочные потери для любых деталей и изделий. Например, как ранее отмечалось, в состав той же самой гусеничной цепи входят два зеркальных звена с ответными отверстиями для деталей «втулка» и «палец» Ø40,87±0,05 м и мм соответственно. Полная стоимость изготовления каждого звена составляет 1051,47 руб. за шт. Если для первого отверстия номинальное значение принять за целевое, а для второго в качестве целевого значения выбрать середину поля допуска, то есть Ø70,06 мм, то значения коэффициентов c будут равны 420 588 и 292 075 соответственно. Для одного из стабильных однородных участков контрольной карты индивидуальных значений, которая велась продолжительное время, среднее значение для диаметра 40,87 равнялось 40,8662 мм, а стандартное отклонение – 0,010918 мм, и для диаметра 70,00 мм – 70,0611 мм и 0,017628 мм соответственно. Количество каждого звена также составляет по 38 «левых» и «правых». Таким образом, получаем, что суммарные потери по Тагути при расчёте относительно меньшего диаметра при сохранении системы в таком же статистически управляемом состоянии составят:

5 = 2■38■420 588(0,0109182 +

+ (70,0611 - 70,Об)2} = 6946,05 (руб.)

соответственно, а их сумма составит 11 217,90 руб. С учётом оценок потерь по Тагути для деталей «палец» и «втулка» совокупная оценка потерь в текущих условиях составляет 58 388,20 руб., что почти 33% от стоимости конечного изделия.

Влияние вариабельности систем измерений на оценку потерь по Тагути.

Руководствуясь теми же соображениями, что были в разделе 4 настоящей статьи, из (19)

получаем:

.         (21)

.

В данном случае представляет интерес отношение S (суммарный уровень потерь с учётом вариабельности системы измерений) к S₀ (суммарный уровень потерь без учёта вариабельности системы измерений). При этом разность между средним и целевым значениями (     )

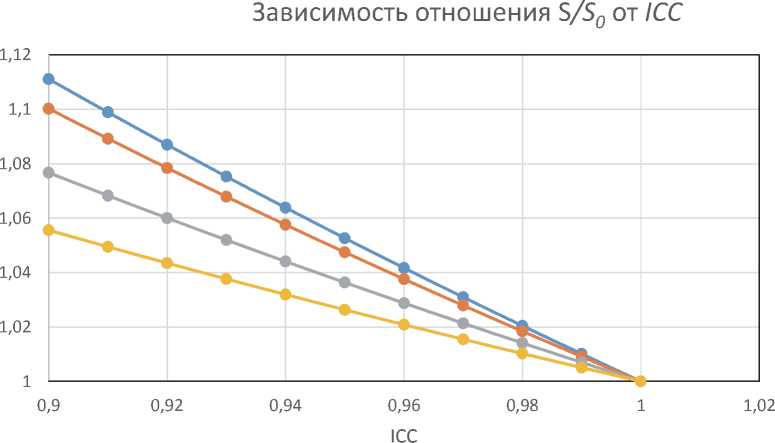
также будем выражать в стандартных отклоне-s ниях. Графики зависимости от ICC для различных значений (     ) представлены на ри сунке 5.

Из рисунка 5 следует, что влияние вариабельности системы измерений на оценку потерь по Тагути тем выше, чем меньше разность между средним и целевым значением. При этом системы измерений I класса (ICC ≥ 0,99) на оценку потерь по Тагути оказывают влияние менее 1 % вне зависимости от разности между средним и целевым значением. Для систем измерений II класса (0,99 > ICC ≥ 0,96) рост оценки потерь по Тагути уже составляет до 4 % при со- впадении среднего и целевого значения, а для систем измерений III класса при ICC = 0,90 эта разница может составить до 11 %. При этом в предыдущем разделе мы убедились, что в условиях реального производства при выпуске годной продукции ожидаемые потери по Тагути могут составлять существенную долю от себестоимости, а совокупные потери, которые могут нести производитель и потребитель вместе на этапе эксплуатации конечного изделия могут составить более четверти от стоимости этого изделия.

—    -

—•— х-т=о

—е—Х-Т=о,33а

--       —  —

—•—Х-Т=0,67а

—

—• Х-Т=а

Рис. 5 – Зависимость оценки потерь по Тагути с учётом вариабельности системы измерений к зависимости потерь по Тагути без учёта вариабельности системы измерений

• 6.    НЕКОТОРЫЕ СООБРАЖЕНИЯ ПО РЕЗУЛЬТАТАМ ПРОВЕДЁННОГО ИССЛЕДОВАНИЯ ПРИМЕНИТЕЛЬНО К СЛОЖНЫМ СИСТЕМАМ

В предыдущих разделах данной статьи рассматривались отдельные характеристики отдельно взятых деталей на финальной стадии изготовления конечной продукции. При этом оценивалось качество только одного параметра – внешнего диаметра деталей «палец» и «втулка». Конечно, даже у таких простых деталей гораздо больше важных характеристик, например, твёрдость, не все из которых можно определить, вопреки широко распространённой точке зрения, а тем более измерить с желаемой точностью. Там, где есть возможность измерения, это может быть либо очень дорогой, либо разрушающий метод, например, толщина функционального покрытия. При этом интерес для конечного потребителя представляет не качество отдельных деталей, а качество конечного изделия, состоящего из множества деталей. Ясно, что потери, которые несут потребитель и производитель из-за качества производственных процессов на всех стадиях производства и эксплуатации весьма значительны. Оценивать и совершенствовать качество производственных процессов следует при помощи ККШ. Только они позволяют определять уровень вариабельности, а также наличие особых причин, которые говорят о том, что процессы находятся в неуправляемом со статистической точки зрения состоянии.

Особое внимание в контексте применения подхода Тагути к оценке качества следует уде- лить целевым значениям процессов. Не стоит путать целевое значение с номинальным значением. Номинальные значения представляют собой опорные значения в рамках допускового подхода, а к целевым значениям ближе всего по своей сути оптимальные значения. Однако, оптимальные значения для отдельно взятых параметров, как и всё в этом мире, подвержены вариабельности. Об этом, а также о том, как Toyota постоянно ищет оптимальные значения, написано Майком Ротером в книге [10]. Кратко суть сводится к тому, что по каждому контролируемому параметру ведётся ККШ, а настройка процесса постоянно меняется то в одну, то в другую сторону относительно текущего положения, но в пределах поля допуска (если, конечно, допусковый подход вообще применим в данном контексте). При этом ведётся постоянный мониторинг качества эксплуатации изделий. И если выявляются положительные (или отрицательные) устойчивые тенденции, то оптимальное, а вместе с ним и целевое значения пересматриваются. Так постоянно и непрерывно совершенствуется процесс производства сложных изделий наивысшего качества при минимальных потерях на всех стадиях жизненного цикла.

ВЫВОДЫ

Показано, что ИВП по Тагути имеют существенное преимущество с точки зрения оценки качества процесса при наличии целевого значения (см. рис. 1). Кроме того, существенное влияние на значение ИВП по Тагути оказывает вариабельность систем измерений, причём для более точно настроенных и менее вариабельных процессов это влияние более существенно.

На данных реального процесса выявлена зависимость оценки потерь по Тагути от качества системы измерений. Оценка потерь от ненадлежащего качества в деньгах позволяет

• -    суммировать потери, вызываемые различными факторами;

• -    разговаривать со всеми лицами, принимающими управленческие решения, на одном языке.

Для реализации такого подхода большинство сотрудников предприятия должны не только понимать ККШ, но и уметь их строить, и принимать на их основе управленческие решения. Но, возможно, самое сложное - это отказ от до-пускового мышления в пользу подхода, предложенного Г. Тагути, и опирающегося на идеи У. Шухарта и Э. Деминга, что по сути означает смену парадигмы управления качеством.