Оценка качества работы операторов ЦОВ по длительности обслуживания вызовов
Автор: Лихтциндер Борис Яковлевич, Татаринова Наталья Михайловна
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Технологии телекоммуникаций
Статья в выпуске: 2 т.9, 2011 года.
Бесплатный доступ
В статье рассмотрен способ применения алгоритма Leaky Bucket для центров обслуживания вызовов (ЦОВ). Разработан алгоритм оценки качества работы операторов с точки зрения длительности обслуживания вызовов для разных режимов загрузки операторов. Приведен пример оценки качества работы группы операторов «Службы технической поддержки пользователей услуги Internet» компании ОАО «ВолгаТелеком».
Качество работы операторов цов, алгоритм leaky bucket, средняя длина очереди, нетерпеливые клиенты, максимальное значение длины очереди, нормативное время обслуживания вызовов
Короткий адрес: https://sciup.org/140191464
IDR: 140191464 | УДК: 621.395.4
Текст научной статьи Оценка качества работы операторов ЦОВ по длительности обслуживания вызовов
Качество обслуживания клиентов зависит от того, как оператор работает на линии. С точки зрения клиента, ЦОВ работает хорошо, если время ожидания соединения с оператором минимальное и предоставленная информация удовлетворяет запрос клиента (получение ответа на заданный вопрос, обслуживание грамотное и вежливое). Для управляющих центрами обслуживания вызовов важным показателем работы операторов является очередь, образующаяся к группе операторов. Увеличение очереди может происходить либо из-за увеличения нагрузки на call-центр (интенсивности поступления вызовов), либо из-за уменьшения интенсивности обслуживания. Обычно очередь измеряют на некотором промежутке времени At , определяя коэффициент загрузки операторов p и характеристики времени обслуживания // (средняя интенсивность обслуживания вызовов) и его дисперсию. Эти величины полностью характеризуют длину очереди лишь при пуассоновском входном потоке и достаточны для оценки степени удовлетворенности клиента, с точки зрения длительности его обслуживания.
Длина очереди при пуассоновском инепуассоновском входящем потоке
Рассмотрим многоканальную систему массового обслуживания (СМО) с ожиданием и неограниченной очередью M/M/N в стационарном режиме. Вероятность того, что в системе находится s требований на обслуживание, определяется по формулам [1]:
где
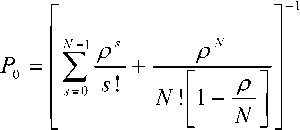
^Q – вероятность того, что в системе отсутствуют требования (клиенты), N – число обслуживаю- щих приборов, p =
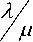
– коэффициент загрузки системы
Среднее число требований в очереди на обслуживание определяется следующим образом:
TV p
Pn'
где PN – вероятность того, что в системе находится ровно N требований. При непуассоновском входном потоке параметры (1) неточно характеризуют очередь.
Текущая очередь и ее изменения во времени могут быть измерены. Рассмотрим систему типа
G/G/1 с дисциплиной обслуживания FIFO. Выбираем на оси времени произвольный момент, обозначаемый t0 . Поскольку поток стационарный, выбор начального момента времени не имеет значения. Рассмотрим интервал времени T (начиная с момента t0 = 0), на котором сохраняется стационарность потока и происходит достаточно большое число событий M . Интервал времени T состоит из периодов занятости и простоя. Каждый период занятости состоит из нескольких интервалов обслуживания вызовов произвольной длины. Пусть случайная величина Q = {r];r2...r,...rA/} – время обслуживания одного вызова. Обозначим число заявок, поступивших в T, -ый интервал обслуживания i -го вызова, через mi , а длину очереди, образующуюся на этом интервале обслуживания, через q. . Очевидно, что длина очереди на интервале обслуживания, предшествующем первому Vo =° и расположенном в периоде простоя, равна нулю.
Длина очереди рассчитывается по рекуррентному соотношению:
q^Qi-x +№,-5^
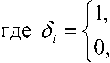
qi-x > 0 или 4i-\ = 0 11
тх >0;
m, = 0.
Подробный вывод (2) описан в [2]. Сбор и анализ статистики значений длины очереди и использование алгоритма Leaky Bucket, больше известного как алгоритм «дырявого ведра», позволяют оценить эффективность работы операторов за выбранный промежуток времени.
Применение алгоритма Leaky Bucket для определения длины очереди и числа нетерпеливых клиентов при нормативной работе операторов
Рассмотрим модель центра обслуживания вызовов с нетерпеливостью клиентов, в которой вызовы поступают согласно закону Пуассона, длительности обслуживания и терпеливости распределены по экспоненциальному закону (модель Эрланг-А) [3]. Данная модель характеризуется четырьмя параметрами: X - интенсивность поступления новых вызовов; p - интенсивность обслуживания; N - число операторов; 0 - интенсивность отказов ( X=w - среднее время терпеливости).
С точки зрения каждого пользователя, время терпеливости w - это время, которое он готов ждать в очереди. При достижении времени ожидания значения w вызов теряется. Тогда по формуле Литтла можно найти предельное значение длины очереди Чтах , при котором пользователи откажутся вставать в очередь и, следовательно, вызов будет потерян:
qmax =^-w.
Следует определить, какова будет длина очереди при данном потоке с интенсивностью x и нормативной интенсивности обслуживания . Нормативная интенсивность обслуживания или обратная ей величина: время обслуживания г„ устанавливаются руководством с целью соблюдения качества обслуживания клиентов.
Разделим рассматриваемый интервал времени на равные промежутки At так, что их общее число r = % будет иметь границы . Обозначим через Чш – длину очереди в момент времени t. , через Чш – длину очереди в момент времени /. , с учетом ушедших клиентов, а через mt – число заявок, поступивших на промежутке времени между t, И t,_x . Допустим также, что обработка заявок на любом промежутке Nt происходит с интенсивностью Ц , равной нормативной. Тогда для длины очереди, с учетом начального условия = 0 и (3), имеет место
среднего нормативного значения длины очереди q^T') и определяется количество нетерпеливых клиентов iH(T) на том же интервале Т при нормативном обслуживании заявок:
iH(T)=t,L.- (7)
Применение алгоритма Leaky
Bucket для оценки качества работы операторов
Рассмотрим длину очереди при реальной интенсивности обслуживания со средним значением . В этом случае начальное условие qo=O останется прежним, нормативные значения параметров заменяются реальными и выражение (4) примет вид:
fq , + m - u • At, q. x^m > u - Nt;
qi=A - (8)
[ 0, qM + m, = jU; ■ Nt;
Так как число обслуженных вызовов на промежутке времени Nt равно пх = цх • Nt , то (8) можно переписать в виде:
ч,
Чни-ц+^-Я,"^
о,
q и + т. > и - At; 1иК!-\) I Hl 7
q ,.+т. = ц - At;
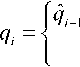
+ тх — пх,
0,
Cli-X + 1Hj > И; ;
5,-1 +«?,. =«,.
где Ч™ =
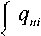
если а . <а ;
Ч max ’
В (8) и (9) значения очереди 4t , с учетом ушедших клиентов, рассчитываются как
^тах ’
если
Чш — Чтах '
Полученное выражение соответствует алгоритму Leaky Bucket, широко применяемому при анализе трафика в потоковых моделях [4]. Число ушедших клиентов при нормативном обслуживании на интервале времени Nt учитывается следующим образом:
4.^
Чтах ’
если если
Ч.<Чтах", Ч.^Чтах-
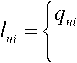
-ч,
О,
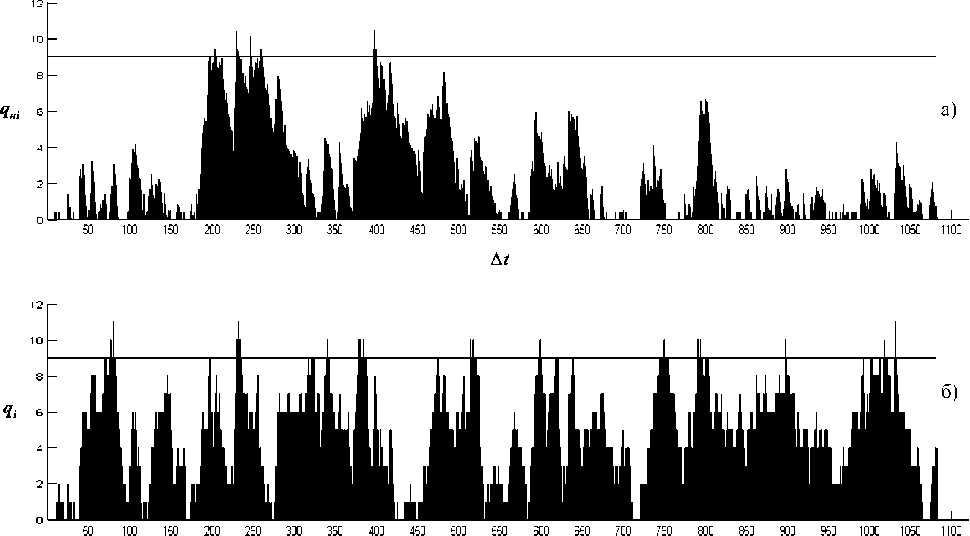
если qM>qM; если qHi Если интервал времени Nt выбрать равным Г„,т04„i примет вид: ^„/ = ^(/-d + w/ “^ где qHi вычисляется аналогично (4), а также I N, [Чни-ц+тс если qHU_xx+mj>N, если qnXi_u+mj Величина nHj в (6) соответствует числу обслуженных вызовов операторами за выбранный промежуток времени. Далее производится усреднение значения 4Hi на интервале T для получения Производя усреднение значений Ч; на том же интервале Т, получим среднее текущее значение длины очереди . Подставляя в (5) вместо нормативных значений 4Hi значения текущие Ч; , получим значения количества нетерпеливых клиентов /z- на каждом отрезке времени At на интервале T. После этого определяется /(7) - число нетерпеливых клиентов на интервале времени T: т=у,1, (Ю) В те часы суток,когда операторы имеют невысокий коэффициент загрузки ( ^опер= 0,5…0,6),доста-точно сравнить нормативное среднее значение длины очереди Qh С^7) с текущим средним значением длины очереди у(Г).Анализ их совпадения или отличия дает представление о качестве работы группы операторов. Действительно, при условии отсутствия перегрузки операторов и их работе согласно норме должно выполняться соотношение: q Если (11) не выполняется и qlPH^, то делается вывод, что показатели работы оператора по длительности обслуживания не соответствуют норме, установленной руководством ЦОВ. При этом, что также важно, определяется величина несоответствия норме. В часы наибольшей нагрузки, когда Ропер ^ ^ , а текущие значения длины очереди qt постоянно превышают значение q^^ , для оценки качества работы группы операторов сравнивают значения нормативного iH (^) и полученное в реальных условиях /(7) числа нетерпеливых клиентов (которое при постоянных параметрах А и ц, можно уменьшить за счет увеличения числа операторов N). Оценка эффективности работы группы операторов ЦОВ компании ОАО «ВолгаТелеком» Для расчетов обрабатывалась статистика поступления и обслуживания вызовов в «Службу технической поддержки пользователей Internet» за 02.04.2010 г. Рассмотрим работу группы операторов, состоящей из N = % человек, на отрезке времени T = 3 ч, предшествующем ЧНН. Данный период характеризуется средним коэффициентом загрузки операторов. Нормативное время обслуживания каждого вызова одним оператором не должно превышать r„ = 4 мин. (рекомендация руководства). За выбранный период времени с 8:00 до 11:00 поступило Л/ = 212 вызовов, все они были обслужены. Реальное среднее время обслуживания каждого вызова г = 4,5 мин. – то есть в среднем, за три часа работы операторов, каждый вызов обслуживался на 30 С дольше нормы, предусмотренной руководством. Зная интенсивность поступления вызовов A, среднее время обслуживания T и число обслуживающих приборов (операторов) N, можно определить коэффициент загрузки каждого оператора: A-т M-г p =---=----= 0,6481. N T-N Разделим рассматриваемый интервал времени 1 = 3 ч на равные промежутки AZ = t„=4 мин., следующие один за другим, общее число которых ' /AZ 45 . Найдем значения числа поступивших т; и обслуженных ”„ И Hj вызовов на каждом промежутке времени AZ . По формуле (6) определим значения нормативной длины очереди Qhi , учитывая, что обслуживание вызовов на любом промежутке M происходит с постоянной интенсивностью Ph , равной нормативной. Далее по формуле (9) определим реальные значения длины очереди q, (на практике эти значения не рассчитывают, а наблюдают в реальном режиме времени). На рис. 1 представлены гистограммы распределения нормативной (а) и текущей (б) длины очереди в течение трех часов. Горизонтальными прямыми на рис. 1 обозначены, соответственно, средние значения нормативной qHm = \,44 и текущей q(T) = 4,38 длины очереди. Рис.1. Гистограммы распределения нормативной (а) и текущей (б) длины очереди Поскольку коэффициент загрузки невысокий: р = 0,6481, для оценки качества работы группы операторов требуется сравнить q„(T) и q(T) . Значение q(T") превосходит ЧНУ^ почти в три раза – это дает представление руководству о том, что операторы обслуживали вызовы медленнее, чем следовало. Подробный анализ значений длины очереди на каждом отрезке kt позволяет оператору постоянно оценивать качество своей работы и стремиться к тому, чтоб средняя текущая длина очереди q^T^ мало отличалась от средней нормативной длины очереди q„(T). Теперь рассмотрим работу той же службы в часы наибольшей нагрузки (с 14:00 до 17:00). В это время работало ^„„=14 операторов, поступило на обслуживаниеM_=519 вызовов, среднее время обслуживания одного вызова ^чин 4,3 мин. Коэффициент загрузки каждого оператора Z? = 0,8581 , при таком режиме работы величина очереди к операторам возрастает и может возникнуть ситуация, когда клиенты не дождутся обслуживания. Поэтому для оценки качества работы операторов мы будем сравнивать число ушедших без обслуживания клиентов, полученное в случае, если бы операторы работали нормативно, с числом ушедших клиентов, полученным на практике. Разделим весь рассматриваемый интервал времени т = з ч на равные промежутки А^„=Ю С, следующие один за другим, общее число кото- рых '-=%,„.=1080. Пусть среднее время терпеливости клиентов w = 240 С, тогда по формуле (3) максимальное значение длины очереди q™x = 9 . Найдем значения числа поступивших mi и обслуженных IT вызовов на каждом промежутке времени Az . По формулам (6) и (9) определим значения нормативной qHi и текущей 4i длины очереди на каждом промежутке м. На рис. 2 представлена гистограмма распределения qHi (а) и ch (б), горизонтальными прямыми показано максимальное значение длины очереди qmax 9 . Число нетерпеливых клиентов при нормативном /H/ и реальном Z; времени обслуживания на каждом AZ определены по формуле (5), а по формулам (7) и (10) было найдено число клиентов, ушедших из очереди без обслуживания, за три часа: /„ = 11 и Z = 28 . Сравнивая значения нормативного Z„ и действительного I числа нетерпеливых клиентов, видно, что при превышении нормативного времени обслуживания каждого вызова на 10 С, число нетерпеливых клиентов при данном потоке увеличивается в 2,5 раза. Чтобы привести показатель z к норме, необходимо увеличить число операторов или увеличить скорость обслуживания вызовов. Выводы 1. При условии средней загрузки операторов (p = 0,5…0,6) оценка разницы значений нормативной и реальной длины очереди на каждом Nt Рис.2. Гистограммы распределения числа нетерпеливых клиентов (а – при нормативном времени обслуживания; б – при реальном времени обслуживания) 2. В часы наибольшей нагрузки, когда Ропер ^ ^ , для оценки качества работы группы операторов сравнивают значения нормативного l„ и реального I числа ушедших без обслуживания клиентов. Число нетерпеливых клиентов, при постоянных параметрахли p,можно уменьшить за счет увеличения числа операторов N. 3. Сравнение средних значений нормативной и текущей длины очереди за длительный промежуток времени (смену работы оператора, неделю, месяц) дает представление руководству о ка- интервале времени At позволяет оператору постоянно оценивать качество своей работы и стремиться к тому, чтобы средняя текущая длина очереди q(T) мало отличалась от средней нормативной длины очереди Qu ^J^ .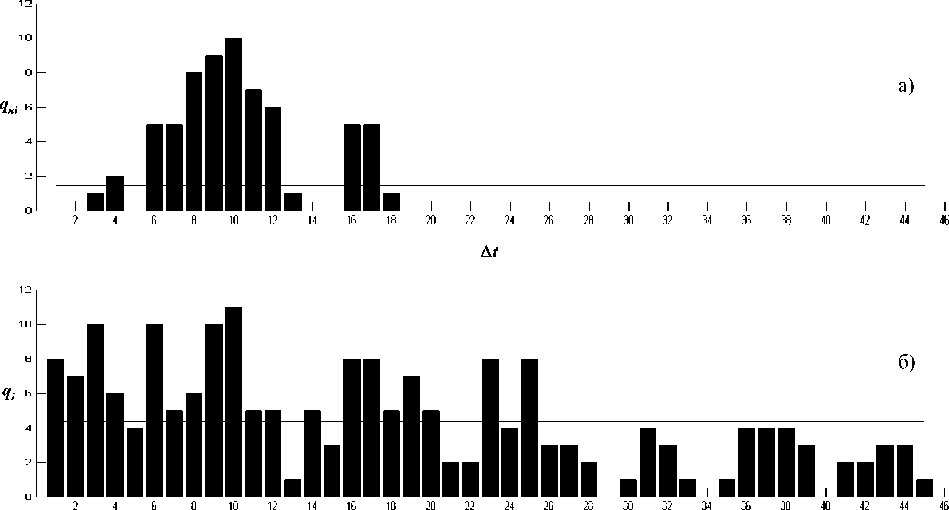
Список литературы Оценка качества работы операторов ЦОВ по длительности обслуживания вызовов
- http://abc.vvsu.ru/Books/imit_model/page0003>. asp.
- Клейнрок Л. Теория массового обслуживания. М.: Машиностроение, 1979. -432 с.
- Росляков А.В., Ваняшин С.В. Математические модели центров обслуживания вызовов. М.: ИРИАС, 2006. -336 с.
- Симонина О.А. Сети ЭВМ и телекоммуникации: методические указания к лабораторным работам (спец. 230102, 230105). СПб.: Изд. СПбГУТ, 2009. -32 с.


