Оценка коэффициента ослабления вибраций от колесных пар на основание кузова электровоза

Введение. Изучению закономерностей формирования спектров вибрации и шума при движении подвижного состава посвящены работы [1–11]. Теоретические и экспериментальные исследования виброакустических характеристик на рабочих местах локомотивных бригад, приведенных в работах [10, 11], показали, что превышение предельно допустимых значений октавных уровней звукового давления в значительной степени определяется структурной составляющей шума.

Обработка результатов экспериментальных исследований. Для уточнения расчета виброскоростей и уровней структурного шума проводились экспериментальные исследования коэффициентов ослабления вибраций

Машиностроение и машиноведение

( k ос ), передаваемых от колесных пар на пол кузова. Методика проведения экспериментов подробно описана в работе [10]. При этом рассматривался более широкий низкочастотный диапазон, поскольку нормирование вибрации на рабочем месте машинистов проводится в этой области частот. При проведении экспериментов выяснилось, что коэффициент ослабления вибрации зависит не только от их частоты, но и от скорости движения электровоза.

Исследования вибрации представляли собой серию экспериментов, в ходе которых значения коэффициента ослабления четырежды измерялись согласно стандартной матрице планирования двухуровневого двухфакторного ПФЭ (полный факторный эксперимент) 2 2 (табл. 1). В последнем столбце табл. 1 указан порядок (на основе генератора случайных чисел) выполнения отдельных опытов при их рандомизации по времени.

Таблица 1

План ПФЭ 2 2

№ п/п	Факторы		Порядок реализации опытов
	х 1	х 2
1	–	–	4
2	+	–	2
3	–	+	1
4	+	+	3

Результаты измерений коэффициента ослабления вибрации представлены в табл. 2.

Результаты экспериментов

Таблица 2

№ п/п	V, км/ч	f, Гц	k ос 1	k ос 2	k ос 3	k oc	( k oc 1    k oc )	( k oc 2   k oc )	( koc 3    koc )	n 2 ^ ( kociu  koci ) и = 1
1	70	8	0,126	0,132	0,120	0,126	0,000E+00	3,974E-05	3,974E-05	7,949E-05
2	100	8	0,204	0,215	0,194	0,204	0,000E+00	1,044E-04	1,044E-04	2,088E-04
3	70	8000	0,180	0,189	0,171	0,180	7,704E-34	8,139E-05	8,139E-05	1,628E-04
4	100	8000	0,161	0,169	0,153	0,161	7,704E-34	6,470E-05	6,470E-05	1,294E-04

Для обработки результатов экспериментов необходимо определить математическое ожидание и среднеквадратичное отклонение по формулам:

1n

k oc i =   ^ k oc i,u ^;

П и = 1

^ ki = ^⁽ kociu  koci )

и = 1

Проведем оценку статистической однородности результатов эксперимента по критерию Кохрена:

G p

^ ( ^k oc i,u и = 1

^- k oci )

max

Nn         2

2 2 ( k oci,и   k oci )

i = 1 и = 1

т

Здесь i — номера серий опытов (от 1 до N ); u — количество параллельных опытов в серии (от 1 до n ); G p и G m — расчетный и табличный критерии Кохрена для 5-процентной значимости при N сравниваемых и n параллельных опытах:

G p

0 , 00021

0 , 00058

= 0 , 36 <  G _m = 0 , 76.

Таким образом, считаем результаты статистически однородными, т.е. соответствующими нормальному распределению.

Определим дисперсию воспроизводимости в натуральных переменных по формуле:

Sk

Nn         2

K^lU-k^ ₌ 0 , 00058 ₌ 7 26.10 - 5

N ( n - 1 )           4 ( 3 - 1 )     ^,         .

Результаты измерения коэффициентов ослабления вибрации (их средние значения) представлены на рис. 1.

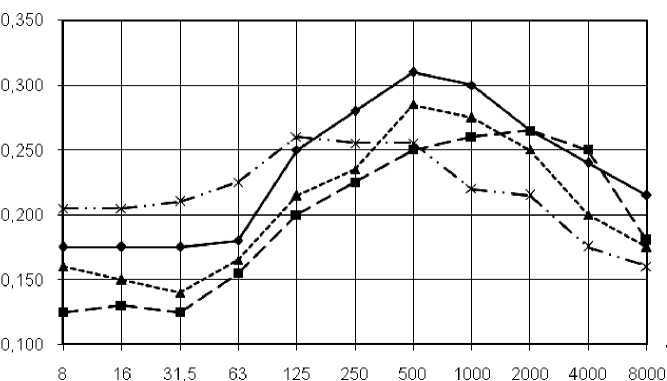
Рис. 1. Коэффициенты ослабления вибраций при скоростях движения: 1 — 80 км/ч; 2 — 70 км/ч;

3 — 90 км/ч; 4 — 100 км/ч

f ,Гц

Определение регрессионных зависимостей. Анализ результатов экспериментов показывает, что максимальные значения коэффициента ослабления вибраций находятся в среднечастотной области и имеют четкую зависимость от скорости движения локомотива. При этом просматривается интересная особенность — с увеличением скорости движения локомотива экстремум кривых смещается в область более низких частот. Так, для скорости 70 км/ч экстремум находится на частоте 2000 Гц, а при скорости 100 км/ч — 125 Гц. Эта особенность осложняет поиск аналитической зависимости функции частотнозависимого коэффициента ослабления вибрации, поэтому принято приближение экстремума всех кривых к частоте 500 Гц, поскольку разница между экспериментальными и расчетными данными незначительна.

Изменение коэффициента ослабления вибрации в зависимости от скорости движения также позволяет выявить экстремальное значение, особенно в среднечастотной области, на скорости 80 км/ч. Таким образом, функция экстремальна по двум координатам, и ее можно аппроксимировать как функцию двух переменных, так как выполняется условие ортогональности, обеспечивающее получение независимых оценок коэффициентов регрессии и их дисперсий [12].

Экстремальность функции в обеих плоскостях требует применения квадратичной аппроксимации или нахождения степенной функции адекватного поведения. При этом необходимо учитывать, что один из факторов, а именно частота f , является величиной геометрического ряда, последующие значения которого увеличены в 2 раза по сравнению с предыдущим. Для смягчения влияния этого параметра его необходимо прологарифмировать.

Таким образом, учитывая экстремальность функции и необходимость логарифмирования входных факторов, принято решение аппроксимировать зависимость степенными функциями. Для этого можно использовать метод перевала, который состоит в построении двух полнофакторных экспериментов таким образом, что значение факторов, обеспечивающих оптимум параметра выхода, является общей границей интервалов их варьирования, поставленных с двух сторон оптимума.

Границей интервалов являются значения факторов, находящихся в экстремуме функции. В данном случае определены следующие интервалы:

• —    для первой области — f = 8–500 Гц, V = 70–80 км/ч;

• —    для второй области — f = 500–8000 Гц, V = 80–100 км/ч.

Для крайних точек интервалов необходимо определить выход, т. е. значение коэффициентов ослабления вибрации. Они комбинируются следующим образом (табл. 3):

Таблица 3

Машиностроение и машиноведение

Комбинация выходов при ПФЭ 2 2

x 1	x 2
min	min
max	min
min	max
max	max

В нашем случае такая комбинация имеет следующий вид (табл. 4):

Комбинация выходов для обеих областей

V , км/ч	f , Гц	oc
70	8	0,126
80	8	0,176
70	500	0,25
80	500	0,311

Таблица 4

V , км/ч	f , Гц	oc
80	500	0,311
100	500	0,257
80	8000	0,215
100	8000	0,161

Для получения степенной зависимости необходимо прологарифмировать все параметры модели. Учитывая порядок коэффициента ослабления вибрации, искусственно увеличим его на два порядка. Тогда исходные данные будут следующими (табл. 5).

Таблица 5

Исходные данные для расчета коэффициентов регрессии

ln V	ln f	ln(100· k oc )
4,248495	2,079442	2,533697
4,382027	2,079442	2,867899
4,248495	6,214608	3,218876
4,382027	6,214608	3,437208

ln V	ln f	ln(100· k oc )
4,382027	6,214608	3,437208
4,60517	6,214608	3,246491
4,382027	8,987197	3,068053
4,60517	8,987197	2,778819

При этом уравнение регрессии в кодовых переменных будет иметь вид:

y = b 0 + b 1 x 1 + b 2 x 2 + b ₁₂ x 1 x 2 ,                                                   (5)

где y = In ( 100 ■ k oc ) ; x 1 = InV ; x 2 = In f .

Для нахождения коэффициентов уравнения регрессии необходимо скомпоновать выходы так, как представлено в табл. 6.

Таблица 6

Компоновка выходов для расчета коэффициентов регрессии

y	–y	–y	y
y	y	–y	–y
y	–y	y	–y
y	y	y	y
S 0	2 1	S 2	S 12

S„       S,       S,        2

Тогда b о = "4 0 ; b = -4 1 ; ^b 2 = —; ^b i2 = — .

Таким образом, на основе выше полученных данных, уравнения регрессии в кодовых переменных имеют вид: y = 3 , 014 + 0 , 138 x 1 + 0 , 314 x ₂ - 0 , 029 x 1 x ₂; y = 3 , 133 - 0 , 12 x 1 - 0 , 209 x ₂ - 0 , 025 x 1 x ₂ .

Определим значимость коэффициентов уравнений регрессии сравнением их абсолютного значения с доверительным интервалом:

A b = ta- 4sl < |b |.                                                     (6)

Здесь t _a — критерий Стьюдента для числа степеней свободы v = N ■ ( n - 1 ) (в данном случае при v = 8 и t_a = 2 , 3 );

S b 2 — дисперсия коэффициентов уравнений регрессии:

Sb

S_k ²

N ■ n

7 , 26 - 10 ^{- 5}

4 ■ 3

= 6 , 05 - 10 ^{- 6} .

Тогда A b = 2 , 3 - V 6 , 05 - 10 ^{- 6} = 0 , 057 .

Анализ полученных коэффициентов уравнений регрессии приведен в табл. 7.

Значимость коэффициентов уравнения регрессии

	A b		b i	Вывод
0	0,057	<	3,014	Значим
1		<	0,138	Значим
2		<	0,314	Значим
12		>	0,029	Незначим

Таблица 7

A b		b i	Вывод
0,057	<	3,133	Значим
	<	0,120	Значим
	<	0,209	Значим
	>	0,025	Незначим

Из табл. 7 видно, что коэффициенты при произведении х1 и х2 статистически незначимы, поэтому данными членами уравнений можно пренебречь. Тогда y = 3,014 + 0,138x1 + 0,314x2;              y = 3,133 - 0,12x1 - 0,209x2.

Для перехода от кодовых переменных к натуральным необходимо выполнить следующие замены переменных:

• 2 UnV - lnV_maA

max

• x                                      I ¹ ;

n max n min

X 2 =

2 ( lnf - Inf max ) ₊1

ln fmax

—

ln fmin

Тогда для первого уравнения:

x 1 =

x 2 =

2 ( lnV - 4 , 382 ) 4 , 382 - 4 , 2485 2 ( ln f - 6 , 215 ) 6 , 215 - 2 , 079

+ 1 = 14 , 978 lnV - 64 , 63,

+ 1 = 0 , 484 ln f - 2 , 006.

Для второго уравнения

2 ( lnV - 4 , 605

x = -(-----------) + 1 = 8 , 963 lnV- 40 , 275 ,

• ¹     4 , 605 - 4 , 382

2 ( lnf - 8 , 987

x =-^------- ) + 1 = 0 , 721 lnf - 5 , 483.

• ²    8 , 987 - 6 , 215

Подставляя замену и приводя подобные, получаем уравнения с натуральными переменными:

ln ( 100 •k oc ) = - 6 , 543 + 2 , 069 lnV + 0 , 152 lnf ; ln ( 100 •k oc ) = 9 , 112 - 1 , 075 lnV - 0 , 151 lnf .

Проводим потенцирование и получаем степенные зависимости koc = 1, 4.10-5 V2,069 f0,152;

k oc = 90 , 657 V ^{4 , 075} f ^{4 , 151}

.

Для оценки погрешности полученных зависимостей сравним расчетные и экспериментальные значения коэффициентов ослабления вибрации (табл. 8).

Погрешность расчетных и экспериментальных значений

V , км/ч	f , Гц	oc	к___ oc.р	A , %
70	8	0,126	0,129	2,94
80	8	0,176	0,171	–2,86
70	500	0,25	0,243	–2,86
80	500	0,311	0,32	2,94

Таблица 8

V , км/ч	f , Гц	oc	к___ oc .р	A , %
80	500	0,311	0,319	2,49
100	500	0,257	0,251	–2,43
80	8000	0,215	0,210	–2,43
100	8000	0,161	0,165	2,49

Наибольшая погрешность полученных зависимостей не превышает 3 %.

Графическая интерпретация этой модели представляет собой две поверхности, соединенные в общей точке экстремума исследуемой функции. Для построения этих поверхностей необходимо определить значения промежуточных точек по полученным зависимостям. Точка экстремума не является центром симметрии функции, она смещена по обеим координатам. Поэтому для малых интервалов определим значение одной промежуточной точки, для больших — двух точек. Результаты расчетов сведены в табл. 9.

Машиностроение и машиноведение

Расчетные значения k oc в промежуточных точках

V , км/ч	f , Гц	oc
70	8	0,1297
70	31,5	0,1597
70	125	0,1968
70	500	0,2429
75	8	0,1496
75	31,5	0,1842
75	125	0,227
75	500	0,2801
80	8	0,171
80	31,5	0,2105
80	125	0,2594
80	500	0,3201

Таблица 9

V , км/ч	f , Гц	oc
80	500	0,3188
80	2000	0,2586
80	8000	0,2098
87	500	0,2913
87	2000	0,2363
87	8000	0,1917
93	500	0,2711
93	2000	0,2199
93	8000	0,1784
100	500	0,2507
100	2000	0,2034
100	8000	0,165

На рис. 2 представлена графическая реализация полученных зависимостей.

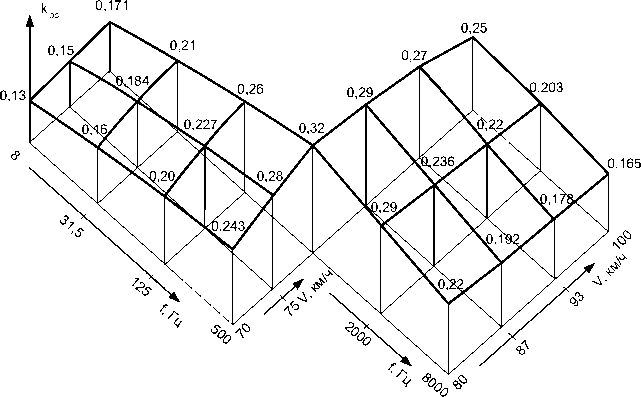
Рис. 2. Влияние скорости движения и частоты на величину коэффициента ослабления вибрации

Выводы. Использование полученных зависимостей коэффициентов ослабления вибрации позволяет упростить расчет и повысить его точность октавных уровней вибрации и звукового давления структурной составляющей шума на рабочих местах локомотивных бригад при различных скоростях движения. Во-вторых, повышается его точность.