Оценка количества апериодических слов

В 1902 г. Уильям Бернсайд поставил вопрос о локальной конечности групп, в которых выполнено соотношение xⁿ = 1 [1]. Впоследствии этот вопрос приобрел статус проблемы Бернсайда. Отрицательный ответ на него впервые был получен в 1968 г. в работах П. С. Новикова -С. И. Адяна [2-4].

Группа B ( d, n ) с d порождающими и тождественным соотношением xⁿ = 1 называется сейчас свободной бернсайдовской группой ранга d и периода n . Ее конечность установлена в разное время для n = 2 (тривиальный случай), n = 3 (У. Бернсайд [1]), n = 4 (У. Бернсайд [1] для d = 2; И. Н. Санов [5] для произвольного d ), n = 6 (М. Холл [6]). Доказательство бесконечности группы B ( d, n ), d > 2, для нечетных показателей n > 4381 было дано в [2-4], а для нечетных n > 665 -в монографии С. И. Адяна [7].

Более подробно с результатами по проблеме Бернсайда можно познакомиться по работе С. И. Адяна [8].

Определение l-апериодическим словом называется слово X, если оно не содержит непустых подслов вида Y.

В монографии А. Ю. Ольшанского [10] доказана теорема о бесконечности множества 6-апериодических слов и получена оценка снизу количества таких слов любой данной длины. Автором в [9] была улучшена оценка из [10] количества 6-апериодических слов в алфавите из двух букв.

В связи с этими результатами рассмотрим множество m -апериодических слов в двухбуквенном алфавите для m > 2.

В статье [11] также получены результаты для 6-апериодических слов над трехбуквенным алфавитом. По этой теме автором опубликованы работы [12-15]. Результаты могут быть применены при кодировании информации в космической связи.

Основные результаты

В 1906 г. А. Туэ установил существование неповторяющихся слов в трехбуквенном алфавите и 3-апериодических слов произвольной длины в любом неоднобуквенном алфавите [11] (см. также лемму 1 в [8]). В статье [16] С. Е. Аршон в 1937 г. доказал существование n -значной асимметричной (повторяющейся) последовательности для n >  3 . В монографии С. И. Адяна [7] представлен метод Аршона для доказательства существования бесконечных 3-апериодических последовательностей в алфавите из двух символов.

В [10] доказана теорема 4.6 о бесконечности множества 6-апериодических слов и получена оценка функции f (n) числа таких слов длины n: в алфавите {a, b} существуют сколь угодно длин ные 6-апериодические слова. При этом количество f (n) таких слов длины n больше чем

n

В связи с этими результатами представляет интерес оценка числа т- апериодических слов в двухбуквенном алфавите.

Случай 2-апериодических слов в алфавите { a , b } легко рассматривается и такие слова можно сразу перечислить:

a, b, ab, ba, aba, bab.

Остальные случаи рассматриваются в теоремах 1-3.

При доказательстве теорем будем использовать метод А. Ю. Ольшанского из [10].

Теорема 1. Алфавит { a, b } содержит сколь угодно длинные т-апериодические слова для т >  5 . При этом количество таких слов длины n больше, чем ( 32 ) •

Доказательство. Сначала докажем неравенство f ( n + 1) >  32 ' f ( n ) по индукции.

База индукции: f (2) >  32 . f (1), где f (1) = 2, f (2) = 4.

Каждое т -апериодическое слово длины n + 1 есть результат приписывания справа одной из букв a или b к т -апериодическому слову длины n . Можно получить 2 f ( n ) слов X длины n + 1.

Но некоторые из полученных слов могут содержать степени A m . Нужно оценить число подобных возможностей.

Может получиться лишь равенство вида X ^ YA^m , поскольку иначе уже начало длины n слова X длины n + 1 содержит A m . Для слов A длины 1 (всего два таких слова) имеется меньше, чем 2 f ( n + 1 - т ) слов вида X = YA m , где слово Y т -апериодично и | Y | = n + 1 - т :

(........ aa... a) a, V '-----v-----' *------- n+1-т

(........ bb ... b ) b.

V *-----v-----* *-------* n+1-т

Существует 4 слова A длины 2. Количество соответствующих слов вида X ^ УА^т длины n + 1 меньше, чем 4 f ( n + 1 - 2 т ), где слово Y т -апериодично длины n + 1 - 2 т .

Аналогично продолжая рассуждения, получаем:

f ( n + 1) >  2 f ( n ) - 2 f ( n + 1 - т ) - 2² f ( n + 1 - 2 т ) - 2³ f ( n + 1 - 3 т ) - ...

Поскольку по предположению индукции f (n) > (32)k ' f (n - k), получается f (n +1) > 2f (n) - (2(%)-т+1 f (n) + 22(%)-2т+1 f (n) + 23(%)-3т+1 f (n) +...).

Вынося f (n) за скобки получаем f (n +1) > f (n )(2 - (2(%)--+1 + 2Ц/!Jт+1

+ ²³(32)

- 3 т + 1

+ ...) >  2 -

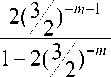
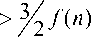
для любых т >  5 (так как ^ 2 <  32 для любого т >  5 , то геометрическая прогрессия в неравен-

- т стве является убывающей со знаменателем 2 ( 3/ ) ).

Следовательно, неравенство f ( n + 1) >  3/2 f ( n ) верно для любых натуральных n для функции f ( n ) количества т -апериодических слов длины n при т >  5 . Теорема доказана.

Из доказательства теоремы 1, в частности, вытекает, что этот способ доказательства не проходит для доказательства оценки f (n) >( 3Д_) функции f (n) количества 3- или 4-аперио-дических слов длины n. В следующей теореме показано, что этот способ не подходит для доказательства оценки f(n) > (x)n и для какого значения x из интервала [32,2] для 3-апериодических слов и из интервала [42,2] для 4-апериодических слов.

Теорема 2. Перенос доказательства теоремы 4.6 о 6-апериодических словах из [10] на случай 3- и 4-апериодических слов не приводит к доказательству соответствующей теоремы, т. е. для любого значения x из интервалов [ 3 2,2] для 3-апериодических и [ 4 2,2] для 4-апериодических слов не удается доказать методом из [10] , что число f_m ( n ) m-апериодических слов длины n больше, чем xⁿ при m = 3 или m = 4.

Доказательство. Проведем рассуждения, аналогичные приведенным в [10]. Но теперь мы не фиксируем значение ( 3/ 2 ) ⁿ для основания показательной функции, а вводим переменную x и ищем оценку в виде f ( n ) >  x n для m = 3 и m = 4.

Сначала докажем неравенство f ( n + 1) >  x • f ( n ) по индукции. При этом введем ограничения на х. Чтобы удовлетворить неравенству f ( 1 ) = 2 >  x для m = 3 и m = 4, подложим x <  2.

База индукции f (2) >  x • f (1), где f (1) = 2, f (2) = 4. База индукции справедлива при x <  2 .

Каждое 3- или 4-апериодическое слово длины n +1 есть результат приписывания справа одной из букв а или b к 3-апериодическому (соответственно 4-апериодическому) слову длины n . Можно получить 2 f ( n ) слов X длины n + 1 ( m = 3 или m = 4). Но некоторые из полученных слов могут содержать степени A ³ (соответственно степени A ⁴). Нужно оценить число подобных возможностей.

Может получиться лишь равенство вида X ^ YA ³ (соответственно X ^ YA ⁴), поскольку иначе уже начало длины n слова X длины n + 1 содержит A ³ (или A ⁴). Для слов A длины 1 (всего два таких слова) имеется меньше, чем 2 f ( n - 2) (соответственно 2 f ( n - 3) слов вида X = YA ³ (соответственно X = YA ⁴), где слово Y 3-апериодично (4-апериодично) и Y = n - 2 (соответственно | Y | = n - 3):

(........ аа ) а , (........ bb ) b для случая 3-апериодических слов;

n - 2                n - 2

( „...„ . ааа ) а , ( . ...... . bbb ) b для случая 4-апериодических слов. n - 3                n - 3

Существует 4 слова A длины 2. Количество соответствующих слов вида X ^ YA ³ (соответственно X = YA ⁴) длины n + 1 меньше, чем 4 f ( n - 5) (соответственно 4 f ( n - 7)), где слово Y 3-апериодично длины n -5 (соответственно 4-апериодично длины n -7).

Аналогично продолжая рассуждения, получаем f (n +1) > 2 f (n) - 2 f (n - 2) - 22 f (n - 5) - 23 f (n - 8) -...

для 3-апериодических слов;

f ( n + 1) >  2 f ( n ) - 2 f ( n - 3) - 2² f ( n - 7) - 2³ f ( n - 11) - ...

для 4-апериодических слов.

Поскольку по предположению индукции f (n) > xk • f (n - k), получается соответственно f (n +1) > 2 f (n) - (2( x )-2 f (n) + 22( x )-5 f (n) + 23( x )-8 f (n) +...) и f (n +1) > 2f (n) - (2(x)-3 f (n) + 22(x)-7 f (n) + 23(x)-11 f (n) +...).

Вынося f (n) за скобки получаем f (n +1) > f (n)(2 - (2(x)-2 + 22(x)-5 + 23(x)-8 +...)

и соответственно

f ( n + 1) >  f ( n )(2 - (2( x ) ^{- 3} + 2²( x ) ^{- 7} + 2³( x ) ^{- 11} + ...).

Введем еще ограничения 3/2 <  x в первом случае и 4/2 <  x во втором для того, чтобы геометрические прогрессии в правых частях неравенств были убывающими.

Обозначим вторые сомножители правых частей за S и применим формулу для суммы членов геометрической прогрессии со знаменателем 4-апериодических слов:

2 x ³ для 3-апериодических слов и 2 x - 4 для

^{- 2}

S = 2--—

1 - 2 x

.-3 ,

S = 2 -         .

1 - 2 x ^{- 4}

Неравенство f ( n + 1) >  x • f ( n ) будет выполняться при S >  x . Преобразуем последние неравенства для обоих случаев:

„ 2 - 4 x ^{- 3} S - x =------

s - x=

- 2 x ^{- 2} + 2 x ^{- 2}

1 - 2 x ^{- 3}

- 2 x ^{- 3} + 2 x ^{- 3}

1 - 2 x - 4

-

x

— >  0, при m = 3 ,

x

— >  0, при m = 4.

После приведения подобных получаем

2 - 4 x ^{- 3}

1 - 2 x

-

. -3

x

-> 0,

2 - 4 x - x „ -------л — >  0.

1 - 2 x - 4

Так как 1 - 2 x ³ >  0 в первом случае и 1 - 2 x - 4 >  0 во втором, получаем неравенства: 2 - 4 x ^{- 3} - x >  0, 2 - 4 x ^{- 4} - x >  0.

Нас интересует решения этих неравенств в интервалах ( 3/2; 2 ) и ( 4/2; 2 ) соответственно. Оказывается, что неравенства в данных интервалах решений не имеют. Теорема доказана.

Как показано в теореме 2 доказательство 1 не проходит для случая m = 4. В следующей теореме докажем, что утверждение теоремы 1 тем не менее верно для m = 4. Для случая m = 3 доказательство таким же методом, как в теореме 3, не проходит.

Теорема 3. В алфавите { а , b } существует сколь угодно длинные 4-апериодические слова. Более того, число f ( n ) таких слов длины n больше, чем ( 3Z ) .

Доказательство. Используем ту же схему, что и в теореме 1, но будем отбрасывать меньше лишних слов.

Заметим, что f (1) = 2 > —.

Докажем неравенство f ( n + 1) > — • f ( n ) по индукции.

_ , 3

База индукции: f (2) >  — • f (1), где f (1) = 2, f (2) = 4.

Каждое 4-апериодическое слово длины n + 1 есть результат приписывания справа одной из букв а или b к 4-апериодическому слову длины n . Можно получить 2 f ( n ) слов X длины n + 1. Но некоторые из полученных слов могут содержать степени A ⁴ . Нужно оценить число подобных возможностей.

Может получиться лишь равенство вида X ^ YA ⁴, поскольку иначе уже начало длины n слова X длины n + 1 содержит A ⁴ . Для слов A длины 1 (всего два таких слова) имеется меньше, чем 2 f ( n - 3) слов вида X ^ YA ⁴, где слово Y 4-апериодично и | Y | = n - 3 :

(^ bbb ) b.

n - 3

На самом деле среди слов Y первого вида нужно брать только те, которые заканчиваются на b , так как иначе уже слово в скобках содержало бы a ⁴, что противоречит его 4-апериодичности. Аналогично среди слов Y второго вида нужно брать только те, которые заканчиваются на a . Таким образом, для слов A длины 1 имеется меньше, чем f ( n - 3) слов вида X = YA ⁴, где слово Y 4-апериодично и | Y | = n - 2.

Существует 4 слова A длины 2. Количество соответствующих слов вида X = YA ⁴ длины n + 1 меньше, чем 4 f ( n - 7), где слово Y 4-апериодично длины n - 7 :

( ....... bb bb bb b ) b.

n - 7

Но такие слова, как в скобках первого и последнего слов уже не содержатся в множестве 4-апериодических слов длины n , поэтому их надо убрать из этого списка. Во втором слове подслово Y длины n -7 не может заканчиваться на a , так как иначе уже слово в скобках содержало бы ( ab )⁴, что противоречит его 4-апериодичности. Аналогично в третьем слове подслово Y длины n - 7 не может заканчиваться на b , так как иначе уже слово в скобках содержало бы ( ba )⁴ . Таким образом, слов вида X ^ YA ⁴ длины n + 1 меньше, чем f ( n - 7), где Y -4-апериодическое слово длины n - 7.

Аналогично продолжая рассуждения, получаем f (n +1) > 2 f (n) - f (n - 3) - ((22 - 2) / 2) f (n - 7) - ((23 - 2) / 2) f (n -11) -...

Поскольку по предположению индукции f (n) > (3/2)k • f (n - k), получается f (n +1) > 2 f (n) - (2 • (3/ 2)-3 f (n) + 22 • (3/ 2)-7 f (n) + 23 • (3/ 2)-11 f (n) +...) +

+ ((3/ 2) ^{- 3} f ( n ) + 2 • (3/ 2) ^{- 7} f ( n ) + 2² • (3/ 2) ^{- 11} f ( n ) + ...) +

+ ((3/2) ^{- 7} f ( n ) + (3/2) ^{- 11} f ( n ) + ...)

Вынося f(n) за скобки, получаем f (n +1) > f (n)(2 - (2 • (3/ 2)-3 + 22 • (3/ 2)-7 + 23 • (3/ 2)-11 +...) +

+ ((3 / 2) ^{- 3} + 2 • (3/ 2) ^{- 7} + 2² • (3/ 2) ^{- 11} + ...) +

+ ((3/2) ^{- 7} + (3/2) ^{- 11} + ...))

Обозначим второй сомножитель правой части за S и применим формулу для суммы членов геометрической прогрессии со знаменателем 2 ( ^^ ) для первой и второй прогрессии и со

- 4

знаменателем I Ч^ I для третьей:

₅ = 2 _ 2(3/2) ^{- 3} + (3/2) ^{- 3} + (3/2) - ⁷

1 - 2(3/2) — 4 1 - 2(3/2) — 4 1 - (3/2) ^{- 4} '

Это значение S приближенно равно 1,58, что больше, чем 3/2. Теорема доказана.

Непосредственно из теорем 1 и 3 вытекает следующее.

Следствие. В алфавите { a , b } существует сколь угодно длинные m-апериодические слова при m >  4 . Более того, число таких слов f ( n ) длины n больше, чем ( 32 ) .

Заключение

Проблема оценки количества апериодических слов до сих пор изучается. Рассмотрено множество m -апериодических слов в трехбуквенном алфавите и получена оценка функции числа таких слов любой заданной длины.