Оценка координат воздушной цели в многопозиционной системе наблюдения "навигационные спутники - воздушная цель - наземный приемник"

В современных условиях все большее распространение приобретают многопозиционные неизлучающие системы наблюдения с подсветом внешним электромагнитным полем. Это обусловлено, во-первых, значительно более высокой живучестью таких систем в сравнении с моностатическими радиолокационными системами, вероятность уничтожения которых противорадиолокационными средствами поражения очень высока, и, во-вторых, более высокой эффективностью многопозиционных систем при обнаружении малозаметных целей, построенных по технологии «стелс» [1]. При этом в качестве подсвета могут быть использованы сигналы различных радиотехнических систем: широковещательных радиостанций, станций ретрансляции телевизионных сигналов, базовых станций сотовых систем связи, а также навигационных спутников глобальной навигационной спутниковой системы (ГНСС) [2-7].

Наиболее перспективными представляются системы с подсветом навигационными сигналами ГНСС, так как в этом случае уже решены многие вопросы, связанные с синхронизацией и координатной привязкой передающих и приемных позиций системы [6-8].

В [8] была исследована энергетика навигационных сигналов, рассеянных воздушной целью, попавшей в зону действия бистатической системы «навигационный спутник – воздушная цель – наземный приемник», и обоснована возможность приема рассеянных сигналов в современном навигационном приемнике наряду с навигационными сигналами прямого распространения. В [9] предложен способ обнаружения рассеянного сигнала на основе алгоритма компенсационного приема полезного сигнала на фоне структурно-детерминированной помехи, а также устройство, его реализующее, как вариант модернизации современного навигационного приемника.

В настоящей статье предложен способ определения координат воздушной цели, попавшей в зону действия многопозиционной системы наблюдения «навигационные спутники - воздушная цель - наземный приемник», как основа построения канала вторичной обработки модернизированного навигационного приемника системы наблюдения.

Постановка задач

В многопозиционной неизлучающей системе наблюдения «навигационные спутники – воздушная цель - наземный приемник» для подсвета воздушных целей используются сигналы навигационных спутников ГНСС С j (j' =1, 2, ..., N , где N >  4) с координатами ( x j , y j , z_}) (рис. 1).

В наземном приемнике П с известными координатами ( х_П, у_П, z_n ) наряду с навигационными сигналами, распространяющимися вдоль прямого пути « j -й навигационный спутник - наземный приемник» с геометрической дальностью r _j ^П (сигналами прямого распространения), принимаются навигационные сигналы, рассеянные воздушной целью Ц с неизвестными координатами ( х, y, z ), находящейся в зоне действия многопозиционной системы наблюдения. Рассеянные навигационные сигналы выделяют на фоне навигационных сигналов прямого распространения одним из оценочно-корреляционно-компенсационных методов [9, 11]. По рассеянным сигналам осуществляется измерение дальностей r _j ^Р вдоль пути распространения « j -й навигационный спутник - воздушная цель - наземный приемник», соответствующее выражение для которых имеет следующий вид:

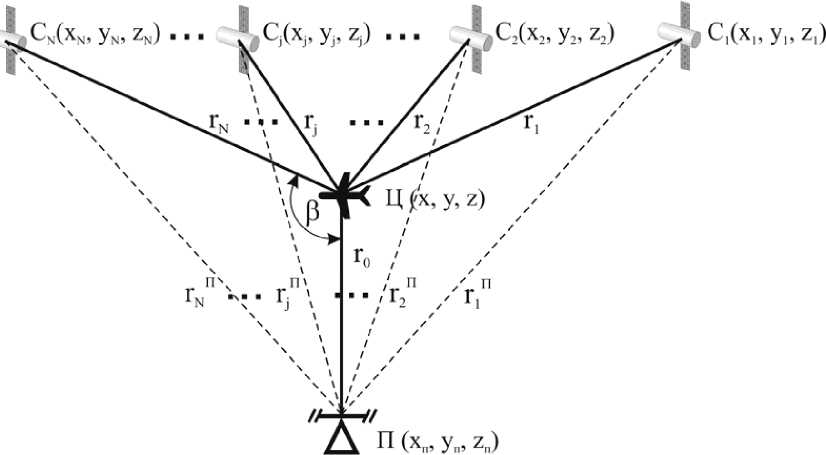
Рис. 1. Многопозиционная система наблюдения «навигационные спутники – воздушная цель – наземный приемник»

rj = rj + r0 + зп + £ =

= [( X j - x ) - + ( y, - У ) - + (z , -z) Г +

1/2

+ [( X - X п )+( y- y п )+( Z - Z п )] + 3 + 8 , где rj - дальность пути «j-й навигационный спутник - воздушная цель»; r0 - дальность пути «воздушная цель - наземный приемник»; 5п - систематическая погрешность измерения дальности, обусловленная смещением шкалы времени приемника относительно бортовой шкалы времени спутников ГНСС; ε – случайная погрешность измерения дальности.

Р

На основании полученных измерений дальностей r _j ^Р требуется определить неизвестные координаты ( x, y, z ) воздушной цели.

Способ определения координат воздушной цели в многопозиционной системе наблюдения

Предложенный способ определения координат воздушной цели, попавшей в зону действия многопозиционной системы наблюдения «навигационные спутники - воздушная цель - наземный приемник», основан на разностно-дальномерном навигационном методе определения координат в аппаратуре потребителя ГНСС [10].

Для реализации этого метода одно из полученных измерений (1), например измерение для 1-го спутника (выбрано условно и не устраняет общности), выбирается в качестве опорного и при составлении системы уравнений соответствующее выражение

Р

r1 = r + r + ^п + е =

= [( х , - х )² + ( у , - у )² + ( z , - z )² f +

1/2

^ X - X п )+( y - уп )+( X-X. ) J  + S, + У вычитается из выражений для измерений всех остальных спутников.

В результате в левой части уравнений записываются разности измеренных дальностей

А т ,' = . j - Г Р ,                                                               (3)

а в правой части уравнений после сокращений одинаковых по величине и противоположных по знаку слагаемых (за исключением случайных погрешностей измерений) остаются выражения для разностей расстояний, пройденных навигационными сигналами вдоль путей распространения « j -й навигационный спутник - воздушная цель» и «1-й навигационный спутник - воздушная цель», включающие известные координаты спутников и неизвестные координаты воздушной цели

2221/2  2221/2

L ⁽ x j — x) + ( y j — y) + ⁽ z j ^- z ) J  +_ ( x ^- x п ) ⁺⁽ y ^- y п ) ⁺⁽ z ^- z п ) J + 5 п + £ ^-

2221/2  2221/2

^-|_ ^{( X} 1 — x) ^{+ (} y 1 — y) ^{+ (} z 1 — z) J ^-|_ ( x — x п ) ⁺ ( y — y п ) ⁺ ( z — z п ) J  — ^ 1 — ^£ =       ⁽⁴⁾

= _ ( X j - x ) ² + ( y j - y ) ² + ( Z j - z ) ² J ¹/² - [ ( X 1 - x ) ² + ( y i - y ) ² + ( Z 1 - z ) ² J ¹/² + £ .

Таким образом, для N спутников, для которых выполняется условие просветной радиолокации (значение бистатического угла лежит в пределах β = 130 – 180° [1], см. рис. 1), получают систему ^из N ^- 1 уравнений

A r P =[( x j - x ) 2 +⁽ y j - y ) 2 +⁽ z , - z ) 2 ] 1/ ^2-

1/2

— [_(xi - x)2 +(yi - y)2 +(zi - z)2 _|   + е, где j = 2, 3, …, N – номер спутника.

Для решения полученной системы нелинейных уравнений воспользуемся итерационным методом наименьших квадратов, для чего запишем систему нелинейных уравнений (5) в ^об об щенном виде:

R = R(q,Q), где R - (N-1)-мерный вектор измерений разностей дальностей; q = [x y z]T - вектор истинных координат воздушной цели; Q – матрица координат навигационных спутников.

Решение системы уравнений (6) методом наименьших квадратов представляет собой процесс многократной (итерационной) обработки результатов навигационных измерений по формуле

-1

q k = q k -i + ⁽ C k -i PC k -i ) C k -i P ^ R k -i ,                                              ⁽⁷⁾

T где qk-1 =( xk-1, yk-1, zk-1) - оценка вектора координат цели на к-1 итерации вычислений; OR к-1 = R - R к-1 - вектор разностей (невязок), измеренных R и рассчитанных на к -1 итерации Rk-1 разностей дальностей; Cк-1 - матрица частных производных от измеряемых навигационных функций по определяемым координатам; k – номер итерационного цикла (как правило, не более 4), P – матрица, обратная корреляционной матрице погрешностей измерений дальностей [10].

Для бистатических разностно-дальномерных измерений элементы вектора невязок δ R _k–1 будут вычисляться по формулам (на примере измерений для j -го спутника):

^>Л т P - j + r„ -1 ,                           ⁸

А j	[ ( xr X k -1 ) 2 + ( yr y k -1 ) 2 + ( z, -z k -1 )	2 r'.	(9)
r .-1—1	Г , x x ) 2 + (       y ) 2 +( z z ) 2 - ^                                                         -	■	(10)
При этом матрица наблюдений C k -1 — [ C 21, k -1 ... C j 1, k -1		T ... C N 1 k -1 1 вычисляется	так же,
как и для обычного разностно-дальномерного метода [10]:
C j i, k -i	— [(cos a , - cos a J (cos pj-cos p}	(cos Y j - cos / 1 ) ],	(11)
где
cos a, j	x j - x k -1        „    yj - У к -1 = .       ; cos P j =   .      ; cos Y j r"j , к -i                              rj , к -i	A = zj^^k -1 , r"j, к -i	(12)

Х - Хм о У - Ум Z\ - Zm cos a = 1. k1 ; cos Д = 1. k1 ; cos /1 = 1. k 1 . (13) ri,k-i ri, k-i ri, k-i

Точность оценки вектора q координат воздушной цели в наземном навигационном приемнике определяется корреляционной матрицей погрешностей [10]

^K q =⁽ C T - PC ^{k - | ) |} - ⁽¹⁴⁾

Методика исследования точности оценки координат воздушной цели в многопозиционной системе наблюдения

Исследование точности оценки координат воздушной цели в многопозиционной системе наблюдения «навигационные спутники - воздушная цель - наземный приемник» с использованием предложенного разностно-дальномерного способа было проведено методом имитационного моделирования. Структурная схема имитационной модели приведена на рис. 2.

В состав имитационной модели входят: модель движения воздушной цели, модель движения навигационных спутников, формирователь вектора измерения, алгоритм определения вектора координат воздушной цели и блок оценки точности определения координат.

В качестве модели движения воздушной цели использовалась траектория полета самолета, сформированная в среде авиасимулятора FlightGear в виде массива значений вектора q истинных координат воздушной цели.

В основу модели движения навигационных спутников положена модель невозмущённого движения спутников [12], исходными данными для которой являются начальные значения орбитальных элементов, а на выходе модели в каждый момент времени формируется матрица Q координат навигационных спутников.

Формирователь вектора измерения реализует алгоритм определения «радиовиди-мых» относительно наземного приемника навигационных спутников ГНСС и формирует ( N -1)-мерный вектор R измерений разностей дальностей в соответствии с (1) - (6) для навигационных спутников, расположение которых относительно наземного приемника и воздушной цели удовлетворяет условию просветной локации [1]. При этом считается, что случайные составляющие погрешности измерения дальности ε представляют собой гауссовские шумы с нулевым математическим ожиданием и дисперсией, соответствующей точностным характери-

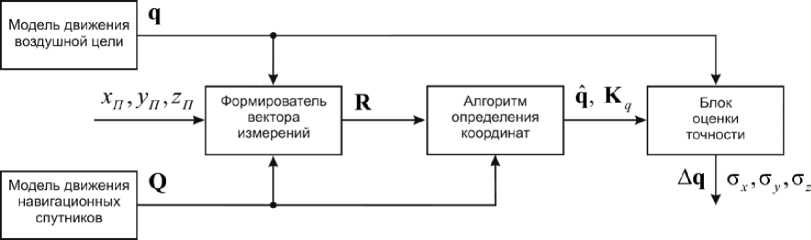
Рис. 2. Структурная схема имитационной модели стикам алгоритмов первичной обработки рассеянных навигационных сигналов в модернизированном приемнике ГНСС [9].

Алгоритм определения вектора координат воздушной цели на основе вектора измерений разностей дальностей R и матрицы координат навигационных спутников Q в соответствии с (7) - (14) формирует оценку q вектора координат воздушной цели и ковариационной матрицы погрешностей K q .

Блок оценки точности определения координат предназначен для определения точности полученной оценки q путем ее сравнения с истинным вектором состояния q и формирования вектора абсолютных ошибок оценки координат

A q = q - q . (15)

Сравнение оценок вектора координат воздушной цели с истиной траекторией осуществляется отдельно по каждой координате и представляется в виде графиков временных зависимо -стей абсолютных ошибок А х = х - х , A y = y - y, A z = Z - z . На этих же графиках отражается динамика изменения СКО формируемой оценки по соответствующим координатам 2с _x , 2с y , 2с _z , где ^ Х ,^\^ 2 - диагональные элементы формируемой ковариационной матрицы K _q погрешностей.

Кроме того, в этом же блоке формируется график временной зависимости абсолютной радиальной погрешности определения координат воздушной цели г-           2                2               2 -|1/2

^{A R} = l ( x - ^x ) ⁺( ^y - y ) ⁺( z - ^z ) I • ^{На этом же} графике Отражается динамика изменения

_ Г_2 . _2 . _211/2

СКО формируемой радиальной погрешности 2с R , где a R = I а x +а _y +а _z I .

Результаты эксперимента

На рис. 3 показана геометрия проведенного численного эксперимента, где сплошной кривой обозначена истинная 3- D -траектория полета воздушной цели типа F-35. Полет воздушной цели осуществлялся в районе аэродрома вылета на удалении не более 5 км и на высоте не более 4 км.

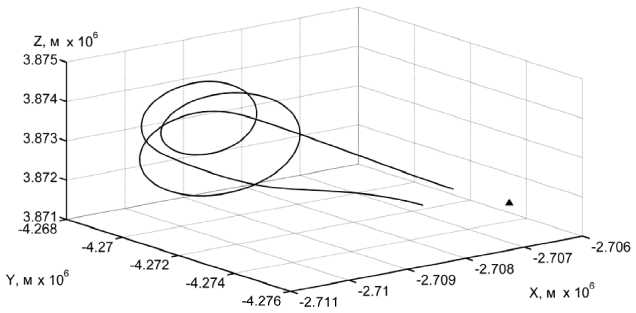
Рис. 3. Геометрия численного эксперимента

На этом же рисунке жирным треугольником показано место установки наземного приемника многопозиционной системы наблюдения. Место положения приемника было выбрано условно, в удалении 1 км по оси X и по оси Y от точки взлета воздушной цели, из соображений попадания траектории ее полета в зону действия системы наблюдения. Координаты наземного приемника ( х_П, у_П, z^ использовались в качестве начального приближения для решения системы уравнений (6). Среднеквадратическое отклонение (СКО) случайной ошибки разностнодальномерных измерений было выбрано σ ε = 5 м и для простоты считалось постоянным на протяжении всего сеанса измерений, т.е. не зависело от ракурса наблюдения и высоты полета воздушной цели.

Результаты проведенного численного эксперимента показаны на рис. 4-7 в виде временных зависимостей значений элементов вектора абсолютных ошибок A q , формируемого на выходе блока оценки точности определения координат. График погрешности получаемой оценки A x приведен на рис. 4 (тонкая линия), где также показана динамика изменения СКО формируемой оценки по соответствующей координате ±2σ x (жирная линия).

Аналогично графики погрешностей A у и A z , а также СКО погрешности формируемых оценок показаны на рис. 5 и 6 соответственно.

Анализ рис. 4–6 позволяет сделать заключение о том, что точность формируемых оценок соответствует расчетному уровню и, в основном, не превышает удвоенного СКО, значение ко -торого составило 10, 9 и 13 м соответственно по координатам x, у , z .

Временная зависимость абсолютной радиальной погрешности определения координат воздушной цели A R показана на рис. 7 (тонкая линия), жирной линией показана динамика изменения СКО формируемой оценки 2σ R . На рис. 7 видно, что точность формируемой оценки соответствует расчетному уровню Δ R ≤ 2σ R и, в основном, не превышает 18 м.

Анализ полученных в ходе имитационного моделирования результатов показывает, что при условии достаточной энергетики рассеянного сигнала и высокой точности дальномерных измерений в канале первичной обработки модернизированного приемника ГНСС использование предложенного способа в канале вторичной обработки обеспечивает точность определе-

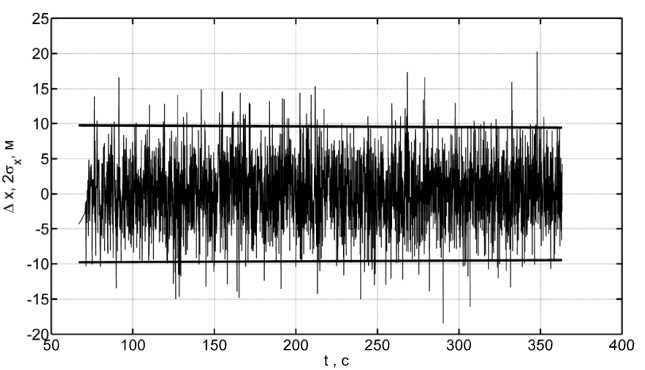
Рис. 4. Точность оценки координаты x воздушной цели

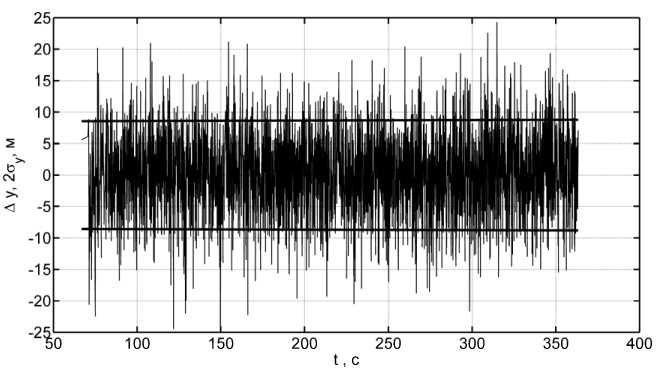
Рис. 5. Точность оценки координаты y воздушной цели

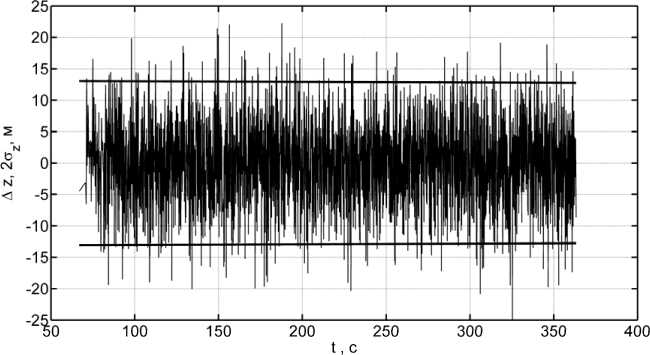
Рис. 6. Точность оценки координаты z воздушной цели

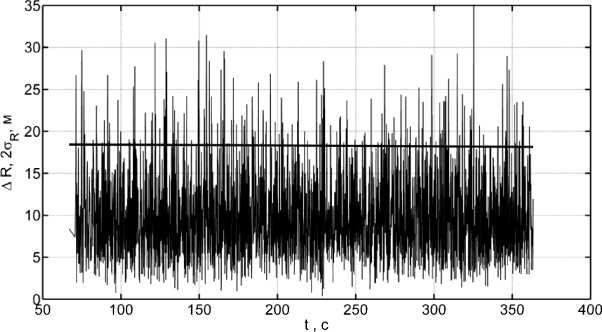
Рис. 7. Временная зависимость радиальной погрешности оценки местоположения воздушной цели ния координат воздушной цели, попавшей в зону действия многопозиционной системы наблюдения «навигационные спутники – воздушная цель – наземный приемник», соизмеримую с точностью оценки собственных координат приемника [12-15].

Заключение

Таким образом, в настоящей статье предложен новый способ определения координат воздушной цели в многопозиционной неизлучающей системе наблюдения «навигационные спутники – воздушная цель – наземный приемник», в основе которого лежит разностнодальномерный метод решения навигационной задачи в аппаратуре потребителя ГНСС. Проведенное с принятыми ограничениями численное моделирование показало, что предложенный способ позволяет с высокой точностью, присущей навигационным методам, определять в наземном приемнике координаты воздушной цели, попавшей в зону действия многопозиционной неизлучающей радиолокационной системы наблюдения «навигационные спутники - воздушная цель - наземный приемник», используя при этом информацию, содержащуюся в рассеянном воздушной целью навигационном сигнале ГНСС.