Оценка квантиля функции распределения времени задержки заявок в однолинейных системах массового обслуживания

Однолинейная система массового обслуживания (СМО) с ожиданием служит хорошей моделью для изучения процессов функционирования многих элементов в сетях электросвязи. Целесообразность выбора экспоненциального закона для описания процесса обслуживания заявок не всегда подтверждается статистическими данными. С другой стороны, во многих случаях экспоненциальное распределение времени обработки заявок - B ( t ) позволяет получить верхние границы многих характеристик для исследуемой СМО. Соответственно, нижние границы можно получить, предполагая, что время обработки заявок постоянно.

Иногда различие между верхней и нижней границами столь существенно, что необходим более точный анализ СМО. Такая ситуация характерна, в частности, для функций распределения длительности задержки заявок - S ( t ) . Более точный анализ СМО может быть выполнен для модели, в которой распределение B ( t ) подчиняется закону распределения Эрланга k -го порядка. При k= 1 эта модель соответствует СМО вида M / M /1 в классификации Кендалла. Данная система позволяет получить верхние границы функции распределения S ^{( t} ) • Если k →∞ , то модель соответствует СМО вида M / D /1, то есть системе с постоянным временем обслуживания заявок. Она используется для оценки нижней границы функции S ( t ). Подбирая величину k в диапазоне ∞>k ≥2 , можно хорошо аппроксимировать многие реальные законы распределения времени обслуживания заявок.

Свойства распределения Эрланга

Плотность распределения Эрланга k -го порядка - b ( t ) определяется следующим выражением [1]:

b ( t ) = k ^ ⁽ k ^ t ) k 1 e^-*^ (k — 1)!

Среднее значение (математическое ожидание) времени обслуживания заявок - B ⁽¹⁾ рассчитывается по такой формуле [1]:

B ⁽¹⁾ = ц ^{- 1} .

Для задач подбора формы распределения B ( t ) существенно то, что математическое ожидание времени обработки заявок не зависит от k . Преобразование Лапласа-Стилтьеса функции B ( t ) — B * ( s ) представимо в следующей форме [2]:

B * ( s )

⎛_⎜ k μ ⎞_⎟ ⎝ s + k μ⎠

Подставив k = 1 , можно убедиться, что все параметры полностью соответствуют экспоненциальному распределению. При k →∞ очевидно, что дисперсия становится нулевой. Это справедливо для постоянного времени обработки заявок. Распределение в этом случае иногда называют вырожденным.

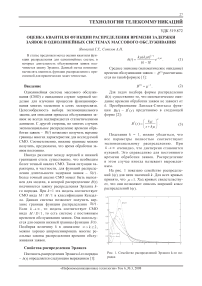
На рис. 1 показано семейство распределений b ( t ) для пяти значений к . Для всех кривых принято, что μ = 1 . Ход кривых свидетельствует, что они позволяют описать широкий класс распределений b ( t ) .

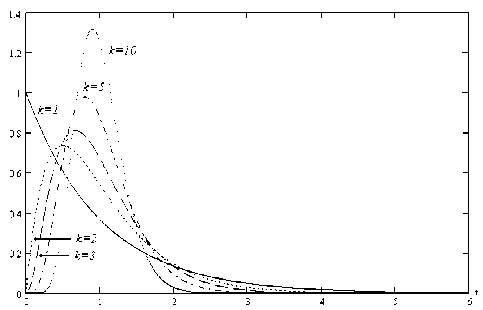
Рис. 1. Семейство распределений Эрланга k-го порядка

Коэффициент вариации времени обработки заявок для распределения Эрланга k -го порядка – C _B определяется так [3]:

После ряда преобразований функция распределе-ниявремени задержки заявок в СМО вида M / E K /1 может быть представлено в таком виде [3]:

го

S(t) = (1 -р)ZИПЧкД)k(i+1) X i=0

Очевидно, что C _B ≤ 1 . Выражения (2) – (4) позволяют рассчитывать многие характеристики СМО вида M / E K /1. Символ E K во второй позиции указывает на вид функции b ( t ) , определяемой выражением (2). Для модели вида M / E K /1 сложно получить функцию S ( t ) . Ее анализ необходим по той причине, что для многих устройств, представляемых в виде СМО, нормируется квантиль функции распределения времени задержки заявок. Поэтому расчет функции S ( t ) - важная для практических приложений задача.

X

i + 1

e" Z p j t i ^- j ⁺¹

j = 1

+ ( - 1) ⁺¹ e ^- k ^ t x

k ( i + 1)

X

Z Q j t k ' j

j = 1

Коэффициенты P _j и Q _j , входящие в формулу для искомого распределения, можно вычислить по формулам [2]:

Функция распределения времени задержки заявок

Преобразование Лапласа-Стилтьеса исследуемой функции S * ( s ) может быть представлено в редакции [3]:

S

го

(s) = (1- р )sZ i=0

( - 1) i X i (k ц ) ^{k ( i + 1)}

(s - X B¹ (s + k ^ ) ^{k (i + 1)}

, (5)

где ρ – загрузка СМО, определяемая отношением интенсивности входящего потока заявок λ к интенсивности их обработки μ . Необходимое условие для работы СМО с ожиданием заключается в выполнении неравенства р <  1.

Дробь под знаком суммы может быть представлена в виде отношения полиномов D 1 ( s ) и D ( s ) . Полином D ( s ) содержит кратные корни: s 1 = X и s ₂ =- k ^ . В [3] для подобных случаев предложено правило нахождения оригинала, на основании которого функцию S ( t ) можно представить так:

го

S(t) = (1 - р)Z (-1)i Х\кц)k(i+1) X i=o(6)

xZ en Z Hn tmn - j - n=1

P _        ( 1) 'C . _ j (i+1 -j)!(X + kд)k(l+X)+j-1,        (9)

c ¹,

Q, =------ —----—.

j ( k ( i + 1) - j )!( 2 + k ц ) ^{i +} j

Для выполнения расчетов по формуле (8) не-обходимоопределитьверхнийпредел суммирования по i . С этой целью целесообразно исследовать функции S ( t ) для систем M / E 2 /1, M / E 3 /1 и M / E 4 /1. Дело в том, что для этих СМО функцию S ( t ) можно получить в более простом виде, исключающем необходимость ограничивать число членов ряда.

Исследование СМО вида M / E 2 /1 , M / E 3 /1 и M / E 4 /1

Классический вид преобразования Лапласа-Стилтьеса функции S ( t ) определяется следующим выражением [1]:

S * ( s ) =

(1 - Р)s s - X + XB (s)

B ( s )

Подставляя в него соотношение для B ( s ) из

(3), для k = 2 можно получить:

Величина m _n равна показателю степени полинома знаменателя - D ( s ) . Возможны всего два значения этой величины: i + 1 и k ( i + 1) . Коэффи-

S * ( s ) = —------ ^{(1 Р)4} ^ ---------.

s ² + s(4^ - X ) + 4ц(ц - X )

циенты H _nj определяются в соответствии с правилами, приведенными в [2]:

Для СМО вида M / E 2 /1 корни знаменателя – s ₁ и s ₂ находятся в результате решения квадратного уравнения:

( j - 1)!(m n - j )! ds j -1

(s - sn )D1 (s)

*                           •

D(s)

(X - 4 ц ) ± V X ² + 8Хц         ....

s i,2 =------------ 2----------- .          ⁽¹²⁾

Несложно убедиться, что оба корня – отрицательные величины при условии, что λ < μ . Те-

перь функция S ( t ) может быть представлена в следующей редакции:

S ( t ) = 1 -

stst s 1 e ² - s ₂ e ¹ 72 ² + 82^

Можно показать, что 0 <  S(t ) <  1 . Вычисление функции S ( t ) для СМО вида M / E 2 /1 по формулам (12) - (13) позволяет приступить к задаче выбора верхнего предела суммирования по i в выражении (8). Предварительно целесообразно получить точные формулы для расчета S ( t ) в двух других СМО - M / E 3 /1 и M / E 4 /1. Для этих систем искомые выражения представимы в такой форме:

k

S(t ) =¹ “ ^ A ( j ’ k )^exP[ s ( Ьk)t ] ,    (14)

j=1

где s ( j , k ) - j корень знаменателя выражения (10) для распределения Эрланга третьего и четвертого порядка ( k = 3, 4); величина A ( j , k ) на основании разложения Хевисайда [2] вычисляется следующим образом:

⁽ P - l)(^k Ц ) k [^{s (} j ,^k ) ^{+ k} Ц ]

^{A (} j , ^k ) _r Ik + 1 , • ⁽¹⁵⁾ [ s( j , k ) + k ц ] - 2 k ( k ц )

В [4] показано, что для больших значений t функцию S ( t ) следует вычислять по приближенной формуле. Она получается из выражения (14) за счет замены суммы по j одним слагаемым. Это слагаемое выбирается за счет поиска минимального по модулю отрицательного корня знаменателя формулы (10) - величины s ( j , k ) .

Для исследования поведения СМО целесообразно оперировать дополнительной функцией распределения V ( t ) = 1 - S(t ). Такой подход эффективен для изучения «хвостов» распределений. На рис. 2 показаны результаты вычисления функций V ( t ) в системе M / E 3 /1.

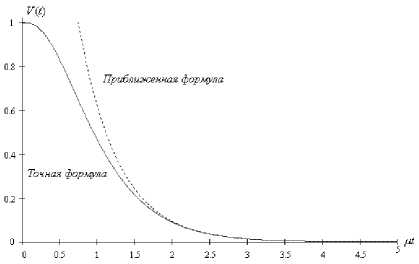
Рис. 2. Результаты вычисления функции V ( t ) по точной и приближенной формулам

Расчеты выполнены для одного значения загрузки СМО: р = 0,1 . При более высокой загрузке расхождение кривых для расчета функции V ( t ) уменьшается. Ось времени нормирована относительно среднего времени обслуживания заявок, то есть на ней отложены величины, измеряемые произведением μt .

Очевидно, что ошибка вычисления функции V ( t ) падает с ростом t . Численные оценки относительной ошибки при расчете функции V ( t ) по приближенной формуле приведены в таблице 1. Она составлена для трех СМО вида M / E K /1 (при k = 2, 3, 4). Вычисления выполнены для двух значений загрузки: р = ^0,1 и Р = 0,9 . Их можно считать границами диапазона реальных изменений загрузки СМО при проектировании систем, исследуемых методами теории массового обслуживания.

Таблица 1. Относительная ошибка оценки V ( t ) по приближенной формуле

μt	M / E 2 /1		M / E 3 /1		M / E 4 /1
	Р = 0,1	Р = 0,9	Р = 0,1	Р = 0,9	Р = 0,1	Р = 0,9
1	3.41 x 10—’	2.69 х 10 - 3	3.28 x 10 - 1	2.08 x 10 - 3	2.52 x 10 - 1	9.56 x 10^
2	1.15 x 10 - ’	1.58 х 10 - 4	4.41 x 10 —2	-1.48 х 10 - 5	-1.62 х 10 - 3	-2.81x10 —5
3	4.40 х 10 - 2	9.35 х 10 - 6	2.49 x 10 - 3	-1.12 х 10 - 6	-3.49 х 10 - 3	5.15 x 10 - 7
4	1.74 х 10 - 2	5.51 x 10 —7	-9.57 х 10 - 4	-2.33 x 10 —9	1.65 x 10 —5	-5.92 х 10 - 9
5	6.99 х 10 - 3	3.25 x 10 - 8	- 3.80 х 10^	5.18x10 —10	6.91 x 10 —5	1.81x10 —11

Данные, приведенные в таблице 1, позволяют сделать два важных вывода, которые существенны для исследования СМО вида M / E K /1 . Во-первых, с ростом k ошибки при вычислении функции V ( t ) уменьшаются. Это означает, что дальнейшее исследование ошибок оценки функции V ( t ) по приближенной формуле для СМО вида M / E K /1 при к >  4 не имеет практического смысла. Во-вторых, для выбранного диапазона изменения загрузки СМО при t >  5B ⁽¹⁾ для оценки значений функции V ( t ) можно использовать приближенную формулу. Относительная ошибка не превысит одного процента, что вполне приемлемо для решения практических задач. Следовательно, задача по выбору предела суммирования по i в формуле (8) интересна для такого диапазона изменения времени: 0 <  t <  5 B ⁽¹⁾ .

Вычисление функции распределения V(t) по точной формуле

Вычисление функции V ( t ) по точной формуле осуществляется только для тех значений времени, которые удовлетворяют условию t ^ 5B ⁽¹⁾ .

Именно с учетом этого неравенства следует выбирать верхний предел суммирования по i в формуле (8) – N . При малых значениях загрузки СМО члены в сумме по i убывают очень существенно. Например, для р = 0,1 достаточно установить так N = 4 , чтобы при t <  5B ⁽¹⁾ ошибка в оценке функции V ( t ) не превышала одного процента. С ростом загрузки СМО необходимо увеличивать значение N . По этой причине исследование зависимости ошибок расчета функции V ( t ) от величины N целесообразно проводить для высокой загрузки СМО. Все технические устройства, исследуемые как СМО, не предназначены для работы с загрузкой свыше 0,9. Именно этот уровень ^ρ целесообразно выбрать для определения значения N .

На рис. 3 показано поведение функции V ( t ) при различных значениях N – от единицы до четырех. Расчеты выполнены для СМО вида M / E 3 /1 при р = 0,9 . Четыре кривые, построенные при разных значениях верхнего предела суммирования по i в формуле (8), показывают слабую зависимость ошибки в расчете функции V ( t ) от N при малых значениях t . Совершенно иная картина наблюдается при t >  2B ⁽¹⁾ . Приемлемая ошибка в диапазоне t <  5B ⁽¹⁾ достигается при N >  4 .

Рис. 3. Поведение функции V(t) при разных значениях верхнего предела суммирования по i в формуле (8)

Численные оценки относительной ошибки при расчете функции V ( t ) для семи значений N приведены в таблице 2. Она составлена для трех СМО вида M / E K /1 (при к = 2; 3; 4). Вычисления, как и для таблицы 2, выполнены при двух значениях загрузки: р = 0,1 и р = 0,9 . Все результаты получены для одной точки на оси «Время»: t = 5B ⁽¹⁾ .

Таблица 2. Относительная ошибка оценки V ( t ) для t = 5B ⁽¹⁾ по точной формуле

N	M / E 2 /1		M / E 3 /1		M / E 4 /1
	Р = 0,1	Р = 0,9	Р = 0,1	Р = 0,9	Р = 0,1	Р = 0,9
1	-0.956	-0.841	-0.989	-0.816	-0.996	-0.798
2	4.152	-2.812	-1.589	27.199	-1.176	2.305
3	-0.015	-0.189	-0.034	-0.086	-0.060	-0.047
4	1.6 х 10 -4	0.021	2.2 х 10 -4	4.8 х 10 - 3	2.6 х 10 - 4	1.6 х 10 - 3
5	-1.1x10 — 6	-1.1x10 — 3	-7.5 х10 - 7	-1.3x10 - 4	-4.9 х10 - 7	-2.4 х10 - 5
6	4.7 х 10 - 9	4.2 х 10 - 5	1.5 х 10 - 9	2.2 х 10 - 6	4.9 х 10 - 10	2.0 х 10 - 7
7	-1.4 х 10 - 11	-1.1x10 — 6	-1.8 х 10 - 12	-2.3 x10 - 8	2.2 х 10 - 12	-8.9 х 10 - 10

Очевидно, что верхний предел в сумме по i при вычислении функции V ( t ) по формуле (8) можно установить как N = 5. Ошибка достигает максимума для СМО вида M / E 2 /1. По мере роста k абсолютная величина ошибки снижается. Это означает, что исследование модели M / E 2 /1 позволяет сделать ряд важных выводов относительно той ошибки, которая обусловлена выбором верхнего предела суммы по i при вычислении функции V ( t ), основываясь на формуле (8). Это утверждение относится к значениям t <  5B ⁽¹⁾.

Выводы

Получены соотношения, позволяющие рассчитывать функцию распределения длительности задержки заявок в СМО вид M / E K /1 . Приведены точная и приближенная формулы, для которых определена область использования и получены оценки ошибок при вычислении искомой функции.