Оценка механических свойств матрицы вокруг частиц наполнителя в полимерных нанокомпозитах с помощью атомно-силовой микроскопии

Дисперсно-наполненные эластомеры (резины) относят к классу композиционных материалов, специфическая особенность которых заключается в том, что их основу составляет непрерывная низкомодульная высокоэластичная полимерная матрица, в которую внедрены твердые зернистые частицы наполнителя (дисперсная фаза) [1-3]. Композиты этого типа как конструкционные материалы появились в начале девятнадцатого века, когда было случайно обнаружено, что наполнение природного (натурального) каучука твердыми частицами микронного и субмикронного размера значительно улучшает его упругое сопротивление и прочностные свойства. Это открытие сделало возможным промышленное использования дисперсно наполненного натурального каучука. В тридцатых годах прошлого века были синтезированы искусственные каучуки различного назначения. Оказалось, что и они способны существенно упрочняться вводом очень мелких твердых наполнителей. Это расширило использование наполненных каучуков в промышленном производстве. В современных резинах в качестве матрицы используются вулканизированные каучуки различных типов, а в качестве наполнителя наиболее распространен технический углерод (черная сажа) [4-5].

В настоящее время известно, что при взаимодействии связующего с частицами наполнителя на них образуются нанослои полимера с особыми механическими характеристиками - связанный каучук [5-6]. Некоторые авторы выделяют несколько слоев полимера вблизи поверхности углерода с разными свойствами. В работе [7] утверждается, что вокруг частиц наполнителя можно выделить два нанослоя - стеклообразный и вязкий. При определенных условиях (когда частицы наполнителя очень мелкие и их концентрация достаточно высока) массовая доля связанного каучука в резине может превышать долю наполнителя и самым существенным образом сказываться на механических свойствах резины [8].

Прямое экспериментальное изучение нанослоев связанного полимера вокруг частиц технического углерода в резине сопряжено со значительными техническими трудностями из-за малости объектов исследований и множества дополнительных искажающих факторов (сложная форма поверхности включений, малые размеры первичных частиц и агрегатов, проблемы с точностью натурных измерений и их интерпретацией и т.д.). Поэтому для решения данной проблемы использовали подход, основанный на сочетании экспериментального исследования полимерных нанослоев на плоской карбонизированной подложке методами атомно-силовой микроскопии и соответствующих модельных расчетов [9].

На сегодняшний день атомно-силовая микроскопия (АСМ) является одним из самых перспективных направлений в изучении структуры материалов на наномасштабном уровне [10]. Главное ее отличие (и преимущество) от других известных методов в том, что она позволяет получать информацию не только о геометрии, но и о механических особенностях строения материала на наноуровне [11-12]. Ее успешно применяют при измерении упругого модуля [13], параметров упрочнения [14], ползучести [15] и т.д. на уровне наноструктуры.

В результате сканирования зондом АСМ поверхности образца были получены экспериментальные зависимости между координатами точек сканирования, действующей на зонд силой реакции F и глубиной вдавливания зонда в материал и . Для дальнейшей теоретической расшифровки этих результатов требуется привлечение различных физических и механических моделей, учитывающих как свойства исследуемой среды (упругая, вязкая, пластическая и т.д.), так и особенности взаимодействия зонда и образца (в котором могут участвовать и силы немеханической природы).

В рамках данной работы рассматривалось только механическое взаимодействие между зондом и образцом. Считалось, что зонд АСМ (который обычно представляет собой кремниевый кристалл) является абсолютно жестким телом, а механическое поведение высокоэластичной полимерной нанопленки можно описать с помощью Неогукового упругого потенциала W :

W = C m ( tr B - 3 ) , (1)

где C m - упругая константа (равная половине начального модуля сдвига материала), B - левый тензор Коши-Грина в полярном разложении деформационного градиента среды.

Контактную краевую задачу о внедрении зонда атомно-силового микроскопа в полимерную пленку с неизвестными механическими свойствами решали методом конечных элементов в осесимметричной постановке. Зонд моделировали в виде конуса со скругленной вершиной радиусом R . При расчетах угол между осью симметрии и направляющей задавали равным 20° (типичное значение для большинства реальных зондов), R брали равным 10 и 20 нм. Полимерные образцы представляли в виде круглых «таблеток» одинакового радиуса 200 нм, но с разной толщиной H , которую варьировали от 5 до 100 нм.

Сверху на зонд действовала сосредоточенная вдавливающая сила F . На границе соприкосновения зонда и образца выполнялось условие полного прилипания без проскальзывания в процессе нагружения. Нижняя граница пленки находилась в абсолютном адгезионном контакте (без отслоений и проскальзывания) с жесткой плоскостью.

Полученные из конечно-элементного решения зависимости были аппроксимированы формулой (2) (с точностью порядка 90 %). Таким образом, зная толщину нанопленки и получив с помощью эксперимента на атомно-силовом микроскопе реальную зависимость F(u) , можно достаточно просто определить упругий модуль материала, подобрав соответствующую теоретическую кривую.

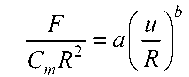
где a = <

b = ^

14,90 ( H/R ) 2,4 + 13,82,

20,45 ( H/R ) ^L525 + 9,00,

0,82exp ( - 1,56 H/R + 0,29 ) + 1,448, '-0,0129 H/R + 1,5085,

0,25 <  H/R <  0,90, 0,90 <  H/R <  10,0, 0,25 <  H/R <  2,25, 2,25 <  H/R <  10,0.

Для бесконечно большой толщины слоя H a = 8,6 и b = 1,3. Эти значения были получены из решения краевой задачи для H / R , равных 30, 40 и 50. Как показали расчеты, на таких толщинах влияние подложки уже не ощущается (все кривые F ( и ) практически совпали). Было установлено, что чем больше значение H , тем меньшие усилия требуются для внедрения индентора на одну и ту же величину (сказывается влияние жесткой нижней границы).

Следует отметить, что часто используемое на практике решение задачи Герца [16] о линейно-упругом контакте двух сфер неприменимо к случаю тонких пленок, так как там не учитывается влияние подложки. Для несжимаемой упругой среды формула Герца, когда одна из сфер имеет бесконечно большой радиус (контакт с плоским полупространством), а вторая абсолютно жесткая с радиусом R , записывается в виде ( G = 2C m - модуль сдвига)

16 GR ^1/2 3/2

F Hertz 3 u ' ⁽³⁾

Сравнение формул (2) и (3) показало, что для полимерной пленки с бесконечно большой толщиной расхождение формулы Герца с нелинейно-упругим решением начинается при значениях u / R > 0,4, причем линейно-упругая зависимость лежит выше.

Технология подготовки экспериментальных образцов для изучения механических свойств нанослоев полимера вокруг частиц технического углерода достаточно подробно изложена в [9].

Сначала готовили карбонизированную поверхность. Для этого на кремниевую пластину с помощью центрифугирования наносили слой полистирола. Затем ее обрабатывали ионами метана в плазменном ионном имплантере. В результате на ее поверхности образовывался карбонизированный слой. Пластину разрезали на маленькие образцы и наносили на них раствор синтетического полиизопрена в толуоле. Образцы с нанесенным раствором подвергали центрифугированию на спинкоатере. Толщину образовавшихся слоев полимера определяли методом эллипсометрии (т.е. по изменению поляризации света в результате отражения от нанопленки). Таким образом, были получены образцы с толщиной полимерного нанослоя 5, 9, 18 и 45 нм.

Для определения опытных зависимостей F ( u , H) использовали атомно-силовой микроскоп DI Nanoscope IV D3100. Измерения проводили в контактном режиме работы АСМ. Полученные результаты представлены на рис. 1.

Исходя из имеющихся экспериментальных данных были приняты следующие расчетные допущения:

• 1.    Считали, что 5-нанометровая пленка полностью состоит из полимера с особыми свойствами, соответствующими модифицированному слою. На это указывает, в частности, исчезновение гистерезиса, ко-

  торый наблюдался у более толстых пленок. Следовательно, решая соответствующую краевую контактную задачу о внедрении зонда АСМ, можно определить механические характеристики этого слоя. Для этого необходимо подобрать такие значения упругих констант, чтобы расчетные и опытные зависимости F ( и ) совпали. Расчеты показали, что подходящее значение C m = C layer равняется примерно 500 МПа, что соответствует начальному модулю Юнга E layer в 3000 МПа. Это соизмеримо с модулем стекла. Похоже, что мы имеем дело с застеклованным полимером, что не противоречит известным литературным данным [7]. В нем нет высокоэластичных областей и нет переходов в кристаллическое состояние и обратно. Поэтому на такой толщине в экспериментах не наблюдается и гистерезиса.

• 2.    Также было принято, что при толщине нанопленки H = 45 нм влиянием этого жесткого застеклованого слоя около углеродной поверхности можно пренебречь, и из решения аналогичной контактной задачи (но уже для 45-нанометровой пленки) можно определить механические свойства несвязанного эластомера, т.е. упругую константу C matrix . В результате проведенных расчетов было установлено, что значение C matrix ~ 40 МПа, т.е. E matrix = 240 МПа. Полученные зависимости приведены на рис. 2.

  

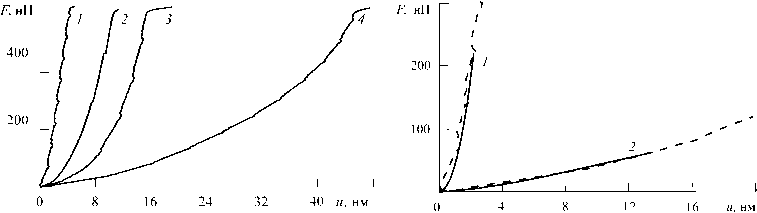
  Рис. 1. Экспериментальные зависимости силы реакции F на щупе АСМ от глубины внедрения и . R = 10 нм, а = 20°:1 - Н = 5 нм, 2 - 9 нм, 3 - 18 нм, 4 - 45 нм

  
  

Рис. 2. Сравнение экспериментальных (штриховые линии) и расчетных (сплошные) кривых F ( и ) для пленок толщиной:

1 - 5 нм, 2 - 45 нм

Далее решали контактную задачу о внедрении зонда АСМ, но уже для двухслойных нанопленок с общей толщиной 9 и 18 нм. При этом для нижнего слоя, прилегающего к подложке, Cm = Clayer = 500 МПа, а для верхнего -Cm = Cmatrix, т.е. 40 МПа. Толщину «модифицированного» слоя Hlayer определяли из условия наилучшего совпадения расчетных и опытных кривых F(и). Сравнение расчетных результатов для двухслойных нанопленок с экспериментом показано на рис. 3. Если использовать данную схему оценки Hiayer, то его значения для 9 нм пленки лежат в диапазоне 5,5-6 нм, а для 18 нм пленки - 9-10 нм. Цифры получились достаточно реалистичные. Наблюдаемое различие в значениях Hlayer, рассчитанных по разным двухслойным пленкам (9 и 18 нм), можно объяснить грубостью используемого подхода. Мы не учитывали неоднородность кристаллизации по объему полиизопрена. В пленке толщиной 9 нм область, в которой формируются с кристаллиты, будет меньше, чем в пленке толщиной 18 нм. В более стесненных условиях кристалличность будет выше и, соответственно, в пленке 9 нм данный слой будет жестче, а в 18 нм — мягче. Это должно привести к более высокой оценке толщины застеклованого слоя в ситуации с пленкой толщиной 18 нм.

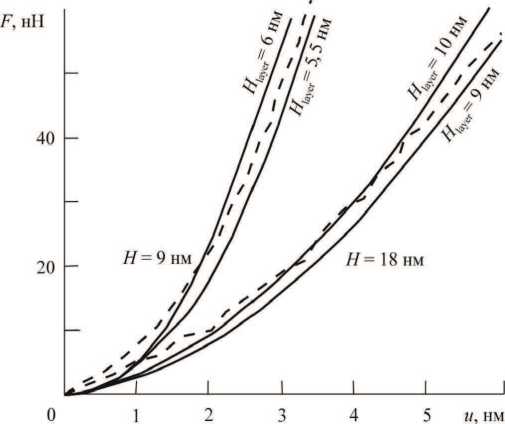
Рис. 3. Оценка толщины модифицированного слоя. Штриховые линии - эксперимент, сплошные - расчет

Кроме того, вполне возможно, что в ультратонких нанопленках имеют место и другие внутренние механизмы, формирующие их механические свойства. Например, не стоит сбрасывать со счетов влияние сил поверхностного натяжения, которые на наноуровне могут достигать очень больших величин. Они находятся в обратной пропорциональной зависимости от кривизны поверхности. Чем тоньше пленка, тем сильнее их влияние и тем большая доля материала пленки вовлекается в деформирование под действием зонда. Мы это почувствуем как повышение силы сопротивления. Ошибочно это можно трактовать как существенное увеличение модуля упругости среды. На самом же деле это еще одно важное физическое явление.

Данная работа это только первый шаг на пути исследования на-номасштабных явлений в полимерных материалах. В дальнейшем планируется усовершенствовать предложенный подход за счет учета сил немеханической природы (взаимодействие Ван-дер-Ваальса, поверхностное натяжение, капиллярные силы и т.д.)

Работа выполнена при финансовой поддержке Программы РАН 09-Т-1-1006 (рук. академик И.Г. Горячева).