Оценка минимального коэффициента безопасности с использованием метода интерполяционных полиномов

Нормативный подход имеет и недостатки. Во-первых, наблюдается традиционность в проектировании. Из-за этого нередко нормативные материалы превращаются в своего рода тормоз на пути совершенствования показателей металлоемкости конструкции. Во-вторых, наблюдается нарушение системного подхода к проблеме. При этом нормативные материалы не охватывают весь комплекс вопросов, связанных с оценкой потребных значений несущей способности, а ограничиваются регламентацией лишь некоторых из них. В существующих материалах основных отраслей техники отсутствуют явные количественные связи нормативных нагрузок и соответствующих поправочных коэффициентов с потребной надежностью конструкций в целом и их частей. В сущности, при таком подходе уровень надежности конструкций оценивается лишь качественно. В-третьих, при реализации детерминистического нормативного подхода не может быть в полном объеме учтено разнообразие условий эксплуатации конструкций, сочетание различных факторов, статистический разброс механических свойств материала, геометрических параметров, начальная дефектность элементов конструкции. Указанные обстоятельства обусловливают повышение удельного веса вероятностных моделей при обеспечении прочности и надёжности.

Статистическая интерпретация нормативных расчетов основана на моделях, использующих элементарные понятия теории вероятностей.

Эти модели вполне применимы, если нагружение представляет собой единичный дискретный акт или последовательность таких актов и можно исключить из рассмотрения временные эффекты, процессы накопления повреждений и т.п. С некоторыми оговорками эти модели могут быть использованы также для нагрузок, непрерывно развертывающихся во времени, если в расчеты ввести распределение максимальных значений нагрузок на всем рассматриваемом отрезке времени.

Установим связь между показателями уровня прочностной надежности, т.е. вероятности безотказной работы, с традиционным для детерминированных прочностных расчетов коэффициентом безопасности f с учетом рассеивания значений тех параметров, которые используются в вычислениях. Установим связь между уровнем прочностной надёжности (вероятности безотказной работы) и традиционными для прочностных детерминистических расчётов коэффициентами безопасности, а также запасами прочности при учёте рассеяния параметров, входящих в расчёт. Условие прочности для элемента конструкции записывается в виде:

Коэффициенты вариации величин записываются следующим образом:

Q = NN,

N   _N ^,

S r =

S R

. R

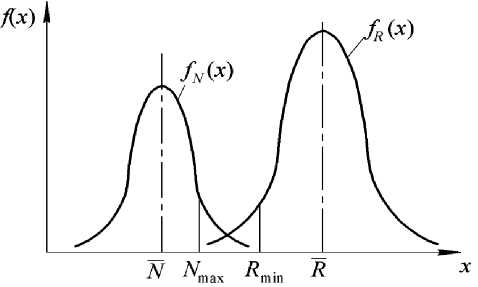
Рис. 1. Плотности распределения нагрузки f N (x) и несущей способности f R (x)

Учитывая (3)-(6) получим новое выражение для коэффициента избытка прочности (1):

П =

^R min

^N m ^p ax

.

где R min – vинимальная несущая способность, N^p max – максимальная расчётная нагрузка.

Для элементов конструкций летательных аппаратов максимальная расчётная нагрузка представляется в виде

„ = ^R min = ^{R   a} R^SR  =

_    N mx   f ( N + « n S n )_

_ r - ад r _ i R 1 - a r

" f ( N + «nS N )" f N 1 + « n N '        (7)

Введём условный коэффициент избытка прочности, со о тве т ствующий отношению средних величин N и R :

pэ max f vmax ,                 (2)

здесь N^э max – максимальная эксплуатационная нагрузка, f – коэффициент безопасности.

В статической постановке связь расчётных (нормативных) величин с учётом рассеяния со статическими характеристиками устанавливается с помощью зависимостей:

R пусл = N"

Запишем выражение коэффициента избытка прочности η с учётом (7) и (8)

П = -П усл

1 — О; R

1 + a N'

N max = N + O v S n , R min = R - a S .

Гауссова мера надёжности находится следующим образом:

Здесь N , R - средние значения нагрузки N и несущей способности R, α N , α R – доли отклонения расчётных величин N^э max , R min от соответствующих значений N и R , выраженные в долях среднего квадратического отклонения, S N , S R – среднеквадратические отклонения величин N и R . На рис. 1 представлены плотности распределения нагрузки N и несущей способности R .

Y 1

Y = STY ” 1TY ’ y = R—N, SY■ = S2 + S2.

С учётом (5), (6) и (8) имеем:

₌ R - N __ N ¹  ₌

^Y   ^S R + S N   ^ S R+ S N

N

П усл — ¹      _     П ул - ¹

I SR R2 + SN N2    SR + пусХ

N ²

+

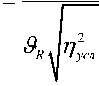
^п усл ^{- 1}

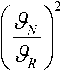
Установим вероятность безотказной работы. При нормальном законе распределения величин N и R вероятность безотказной работы конструкции H можно определить по таблицам функций нормального распределения:

H = Ф    = Ф ( Y ).

V S y 7

Формулы (9) и (10) дают возможность связать традиционный коэффициент безопасности f с вероятностью безотказной работы H . Для этого выражение (10) разрешается относительно η усл :

П усл

R J + 1 1 — ( I — Y3 _R ) 2 [ 1 - ( yS n ) 2

N "           1 - ( YS R ) ²

По заданным статистическим характеристикам нагрузки N и несущей способности R , учитывающим рассеяние этих параметров, можно решать две задачи: определить вероятность безотказной работы конструкции H (11) и условный коэффициент избытка прочности η усл (12); на основании формулы (9) найти минимальное значение коэффициента безопасности, обеспечивающее заданное значение вероятности безотказной работы H конструкции:

1 - ( z_ff R R

f      Пусл             ,

П 1 + «nN

приняв минимально допустимое значение коэффициента избытка прочности.

Для сравнительно простых систем, для которых параметр поведения системы получается оценить с помощью простых формул, для отыскания минимального значения f используется метод линеаризации. Для сложных вырожденных систем, где связь между характеристиками системы, параметром внешней нагрузки и параметром поведения системы не получается выразить в явном виде, используются методы статистической динамики. Одним из таких методов является метод интерполяционных полиномов [3].

Рассмотрим применение изложенного выше подхода совместно с использованием метода интерполяционных полиномов к задаче об оценке минимального коэффициента безопасности при анализе напряжённо-деформированного состояния стыка днища топливного бака ракеты-носителя с обечайкой, подкреплённого шпангоутом. На рис. 2 представлено поперечное сечение шпангоута и примыкающие к нему участки днища и обечайки.

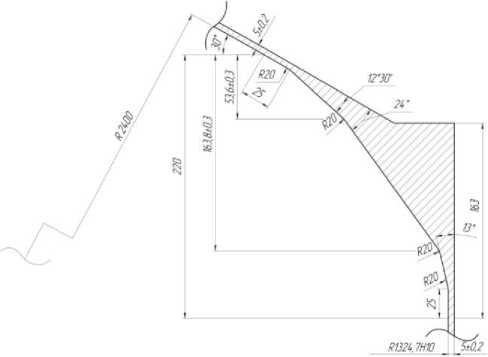
Рис. 2. Схема рассматриваемой конструкции

Первым этапом решения этой задачи является выполнение детерминированного расчёта. В качестве исходных данных для анализа напряжённо-деформированного состояния элемента бака ракеты-носителя берутся значения мат. Ожиданий, приведенных в табл. 1 величин. Для расчёта целесообразно воспользоваться методом конечных элементов. В качестве программного пакета можно использовать пакет ANSYS, позволяющим в дальнейшем реализовать метод интерполяционных полиномов с помощью удобного встроенного языка программирования APDL. Данный программный пакет позволяет выявить опасное сечение, в котором достигаются наибольшие напряжения (рис. 2).

Далее проводится решение задачи статистической динамики для вырожденных систем методом интерполяционных полиномов. В качестве параметра внешнего воздействия берётся давление наддува, действующего в баке ракеты-носителя. В качестве свойств системы принимаются модуль упругости материала E, толщина обечайки δоб., толщина днища δдн., радиус обечайки Rоб., геометрические характеристики шпангоута l1 и l2. За параметр, характеризующий предельное состояние конструкции при котором не происходит её разрушения принимается условный предел текучести σ0,2. Законы распределения и числовые характеристики указанных случайных величин приведены в табл. 1.

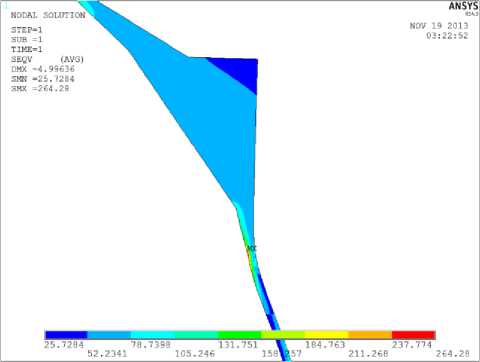
Рис. 2. Опасное сечение элемента конструкции бака ракеты-носителя

В качестве параметра, характеризующего поведение системы, можно принять эквивалентное напряжение, определяемое по одной из теории прочности. В рассматриваемом случае для этих целей выбирается напряжение по Мизесу (или эквивалентное напряжение по теории прочности энергии формоизменения):

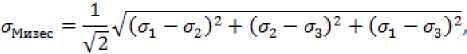
заданный уровень надёжности, методом интерполяционных полиномов следует выполнить следующие шаги:

• 1.    Определяются законы распределения случайных входных величин и их вероятностные характеристики, а также задаётся потребный уровень надёжности (задаётся Гауссова мера надёжности γ , соответствующая потребному уровню надёжности H );

• 2.    Для каждой конкретной реализации входных случайных величин с использованием программного пакета ANSYS определяется напряжённое состояние в наиболее опасном сечении. Выполнив q решений, находятся q реализаций выходного параметра;

• 3.    Проводится статистическая обработка полученных результатов в соответствии с методом интерполяционных полиномов. Определяется математическое ожидание, дисперсия, коэффициенты вариации параметра поведения системы.

• 4.    Определяется условный коэффициент безопасности в соответствии с формулой:

  

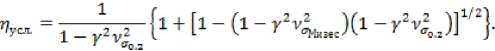
• 5.    Определяется коэффициент безопасности, полагая η =1 по формуле:

У _ ^f^_£2L^fo^£i2_

^  1 ■*" “оМизес ГоМиж здесь σ1≥σ2≥σ3 – главные напряжения.

Для вычисления минимального значения коэффициента безопасности, обеспечивающего

Таблица 1. Параметры распределения

Случайная величина	Закон распределения	Математическое ожидание	Среднее квадратическое отклонение
р	нормальный	(р> = 0,45 МПа	Sp = 0,0067 МПа
Е	нормальный	(Е) = 7 ■ 104 МПа	Se = од (^ МПа
°02	нормальный	(ао,2) = 300 МПа	■^<702 = ОДСоо.г^ МПа
	равномерный	(5об.) = 5,5 мм	5 0- = 0,2 л мм
^дн.	равномерный	<^дн.> = 5,3 мм	= 0,2 т мм
	равномерный	(Zj) = 163,8 мм	— 0,3 мм
^2	равномерный	(Z2) = 53,6 мм	5^2 = 0,3 мм мм
^об.	равномерный	(Яо6.) = 1324,7мм	Sr . = 0,3 лоб.     л мм

Следует иметь ввиду, что это значение коэффициента безопасности обеспечивает тот уровень вероятности безотказной работы конструкции, который соответствует гауссовой мере надёжности γ . В рассматриваемом примере она взята равной 3,72, что соответствует уровню вероятности безотказной работы H =0,9999.

Коэффициенты ^^ол и “^Мизк , характеризующие степень рассеяния случайных величин в долях среднего квадратического отклонения взяты по единице.

Изложенный алгоритм достаточно просто реализуется в том же программном пакете ANSYS, в котором производится расчёт напряжённо-деформированного состояния конструкции. Это возможно с помощью средств встроенного языка программирования APDL. Представленный выше алгоритм можно изобразить в виде блок-схемы, показанной на рис. 3. В табл. 2 приведены результаты, полученные методом интерполяционных полиномов, при выборе по два и по три узла интерполяции для каждой случайной величины. Видно, что сходимость метода достигается уже при использовании двух узлов интерполяции.

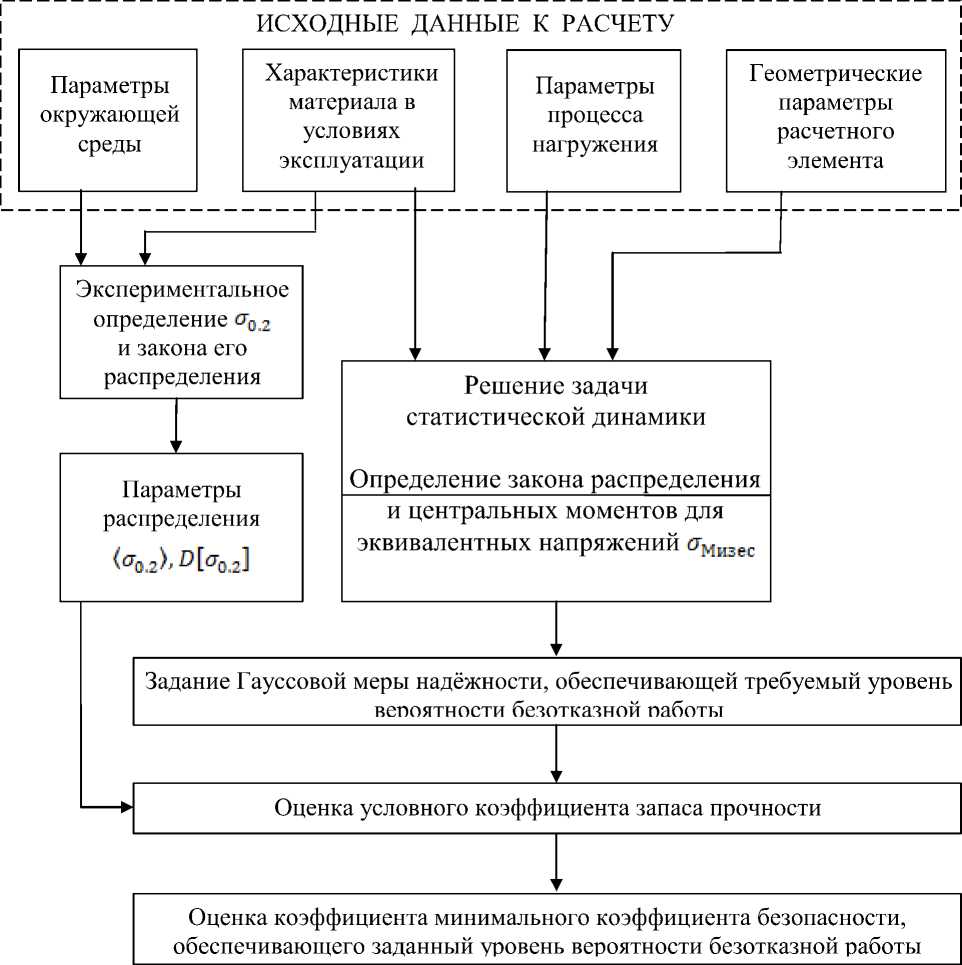
Рис. 3. Блок-схема

Таблица 2. Результаты расчёта

Число узлов	Напряжения по Мизесу		Коэффициент безопасности
	математическое ожидание, МПа	среднее квадратическое отлонение, МПа
2x2x2x2x2x2x2	264,1513	18,8945	1,05895
3x3x3x3x3x3x3	264,3782	19,0878	1,05905

Выводы:

• 1.    Необходимо иметь достоверную и наиболее полную информацию по вероятностным характеристикам свойств системы, параметров

• 2.    Обеспечивать заданную вероятность безотказной работы можно двумя путями: а) добиваться меньшего рассеяния значений параметров свойств системы, параметров предельного состояния и параметров внешних воздействий (т.е. значения случайных величин должны лежать в меньшем диапазоне коэффициентов α ), что в свою очередь приводит к ужесточению условий эксплуатации и технологии изготовления изделия; второй путь заключается в снижении параметра поведения системы, либо в повышении параметра предельного состояния. Добиться этого можно изменяя конструктивные параметры, физико-механические свойства и/или параметры внешнего воздействия.

• 3.    Метод интерполяционных полиномов является эффективным средством решения задачи об определении минимального значения коэффициента безопасности, соответствующего заданному уровню безотказной работы конструкции. Это обусловлено малым числом реализаций случайных величин при достаточной для инженерных расчётов точности, а также возможностью и

• удобством численной реализации данного метода.

предельного состояния и параметров внешних воздействий, как на этапе изготовления изделия, так и на этапе его эксплуатации.

В заключении следует отметить, что изложенный в данной статье подход для оценки минимального коэффициента безопасности применим для широко круга инженерно-технических систем и позволяет не только получать нижнюю границу коэффициентов безопасности, но и анализировать пути и методы повышения вероятности безотказной работы различных изделий.