Оценка мощности полного множества альтернатив паретовских подграфов в графе

На практике задачи построения оптимального подграфа определённого вида в заданном графе встречаются достаточно часто [1–8]. В качестве возможных приложений используются задачи поиска оптимальной структуры технологических сетей, проектирования архитектуры вычислительных устройств, моделирования искусственного интеллекта и многие другие. С формализованной точки зрения наиболее популярны задачи поиска кратчайшего пути и остова минимального веса.

В последние десятилетия всё более актуальными становятся многокритериальные варианты указанных задач. Однако существенным сдерживающим фактором совершенствования методов многокритериальной оптимизации на графах является проблема их вычислительной сложности, вызванной большой размерностью Для цитирования

задачи. Полученные оценки [4, 5] свидетельствуют об экспоненциальном возрастании числа эффективных решений.

Однако мощность множество Парето-оптимальных вариантов редко имеет близкую оценку с числом всех допустимых вариантов решений задачи. Ряд данных свидетельствует, что теоретическая оценка сложности, построенная для методов полного перебора, не соответствует действительности, исделанные выводы не имеют достаточного обоснования.

Поясним сказанное. С любой задачей многокритериальной оптимизации ассоциируется множество эффективных решений X *. Оно состоит из таких допустимых вариантов решения x , для каждого из которых не существует элемента y , лучшего, чем x по всем критерием одновременно, то есть такого, что q j ( y ) ≤ q j ( x )

сразу для всех j , причём, хотя бы одно неравенство является строгим. Среди эффективных решений наибольший интерес представляет так называемое полное множество альтернатив (ПМА) [9] - подмножество X c X * минимальной мощности, такое, что образы q( X *)и q( X ° ) совпадают. Часто мощность множества эффективных решений может быть на порядки выше, чем мощность ПМА.

Кроме того, в практически важных задачах значения оценок по критериям ограничены, а этот факт при теоретическом анализе мощности множества Парето не учитывается.

С учётом перечисленных фактов в данной работе изложен результат исследований попостроению приемлемой оценки сверху для мощности ПМА задачи построения парето-оптимальных подграфов для некоторого графа.

Получение оценки

Пусть задан граф G = ( V, E ), | V | = n , | E | = m произвольного вида, на рёбрах которого заданы значения s критериев q i = q i ( e ), i = 1,…, s; e е E . Значения q будем полагать целыми неотрицательными числами из конечного диапазона [0; d ]. Требуется построить множество Парето-оптимальных подграфов, принадлежащих некоторому определённому виду. В качестве критериев эффективности подграфа предполагается минимум суммы значений критериев рёбер, входящих в подграф, так называемый критерий вида minsum [10].

Предположим также, что количество рёбер каждого допустимого подграфа не превосходит некоторого k, k < m .

Теорема 1. При сделанных предположениях мощность ПМА задачи поиска Парето-опти-мальных подграфов не превосходит

N = ( d • k + 1) ⁵ - ( d • k ) ⁵ .            (1)

Доказательство. Покажем, что мощность ПМА паретовских подграфов не больше, чем число целочисленных точек на s ближайших к началу координат гранях гиперкуба [0, k • d]⁵ .

Обозначим это множество точек Г. Оно имеет следующий вид:

Г =

Л е E^s | 0 < Л < к • d , Л i = 1,..., 5 ; min Л = 0

- целые,

Пусть P – множество достижимых критериальных оценок эффективных подграфов. Построим отображение ф : Р ^ Г следующего вида:

V p е P ф (p ) = p - min p . ^j

Очевидно, что все ф (р ), как и р будут иметь целочисленные координаты, причём min ф ( p ) - = 0. Следовательно, ф (р ) е Г. ^j

Покажем, что ф инъективно, т. е. двум произвольным различающимся точкам p и r соответствуют разные образы. Предположим противное, т. е. элементам p,r е Р соответствует один образ X = ф (р ) = ф ( r ). Из этого сразу следует, что p i – min p i = r i – min r i . То есть p i – r i = =min p i – min r i = a = const для всех i .

Тогда при a < 0 получим p i < r V i . Поскольку p не совпадает с q , то это должно означать, что точка р доминирует по Парето над r . При a > 0 получим обратное отношение. Так или иначе, получаем противоречие с предположением, что обе точки оптимальны по Парето.

В итоге получаем, что, отображение ф между Р и Г инъективно, из чего следует | Р | <  |Г|.

Оценим значение |Г|. Количество точек вдоль каждой из координат равно ( k - d +1). Тогда количество точек, заполняющих весь s -мерный куб равно ( d • k +1)^s. Для оценки мощности Г от этого числа надо отнять количество узлов, заполняющих вложенный куб, из d • k точек по каждой координате, т. е. ( d • k ) ⁵ . Окончательно |Г| = N = ( d • k +1) ⁵ - ( d • k ) ⁵ . Теорема доказана.

Предположим, что количество критериев s ограничено некоторой константой. Тогда из (1) вытекает, что мощность ПМА паретовских подграфов ограничено некоторым полиномом.

Оценку (1) можно уточнить, если есть возможность определить диапазоны значений по каждому частному критерию [q™ш, q;max]. Парето-оптимальных подграфов данного вида. Используя результаты теоремы 1, несложно показать, что в этом случае мы имеет следующую верхнюю оценку мощности ПМА Парето-опти-мальных подграфов ss n=П( q-max - q-m,n +1) - П( q™ - q-m,n) • (2) i=1 i=1

Пример

Рассмотрим следующий ориентированный граф, на дугах которого заданы два критерия (их численные значения указаны в скобках).

В качестве подграфов будем рассматривать стягивающие остовы графа. Найдём в этом графе все Парето-оптимальные остовы. Для их компактного представления перенумеруем дуги графа согласно таблице 1.

Согласно известной оценке [10], основанной на матрице инциденций исходного графа, легко определить, что граф, представленный на рисунке 1 имеет 101 остовное дерево. Отсюда полным перебором несложно найти его Парето-оптимальные остовы, список которых приведен в таблице 2. В данном случае ПМА паретовских остовов совпадает со списком всех тринадцати Парето-оптимальных остовов.

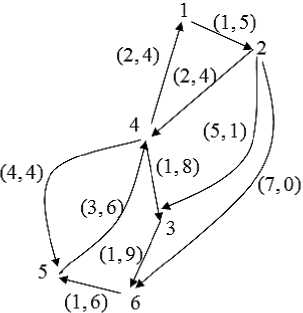
Рисунок 1. Пример графа с заданными двумя критериями на его дугах

Figure 1. An example of a graph with two given criteria on its arcs

Таблица 2.

Список Парето-оптимальных остовов

List of Pareto-optimal Islands

Таблица 1.

Список дуг графа

Table1.

The list of arcs of the graph

No	Начальная вершина Initial vertex	Конечная вершинаFinal vertex	Значение Value q 1	Значение Value q 2
1	1	2	1	5
2	2	3	5	1
3	2	4	2	4
4	2	6	7	0
5	3	6	1	9
6	4	1	2	4
7	4	3	1	8
8	4	5	4	4
9	5	4	3	6
10	6	5	1	6

Table 2.

No	Номера дуг, составляющих остов Numbers of arcs that make up the skeleton					Значение 1-го критерия Value of the 1st criterion	Значение 2-го критерия Value of the 2nd criterion
1	1	2	3	4	8	19	14
2	1	2	3	4	10	16	16
3	1	2	3	5	10	10	25
4	1	2	3	8	10	13	20
5	1	2	3	9	10	12	22
6	1	3	5	7	10	6	32
7	1	3	7	8	10	9	27
8	1	3	7	9	10	8	29
9	2	3	4	6	8	20	13
10	2	3	4	5	10	17	15
11	2	3	5	6	10	11	24
12	2	3	6	8	10	14	19
13	3	5	6	7	10	7	31

Сравним реальное количество остовов с оценкой (2). Имеем следующие диапазоны, которые несложно найти, например, посредством алгоритма Краскала [10]:

min max

[ qi   , qi   ] = [6,20]

,

[ q m\ q max] = [14,32]

Отсюда по формуле (2) получаем

N = 33 >  13. Следовательно, оценка (2) справедлива.