Оценка надежности дорожного покрытия при воздействии предельной нагрузки с позиции механики разрушения

Для описания процесса разрушения лесовозных [2] автомобильных дорог могут быть использованы структурные либо полуэмпи-рические модели. Структурные модели основаны на математическом описании физики процесса накопления повреждений на одном либо нескольких уровнях структуры [6], [7]. Развитие процессов поврежденности зависит как от внутренних, так и от внешних причин. Разрушение дорожных одежд лесовозных автомобильных дорог [1] в данном случае будем рассматривать вследствие появления трещины предельных размеров при однократном приложении нагрузки.

Раскрытие трещины в твердом теле может быть осуществлено одним из трех известных путей (рис. 1): при нормальных напряжениях возникает трещина типа «разрыв» (тип I), при плоском сдвиге образуется трещина типа «сдвиг» (тип II), при антиплоском – типа «срез» (тип III).

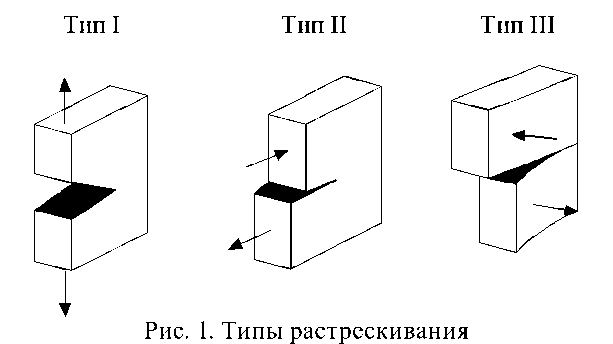
Примем допущение, что при взаимодействии колеса с поверхностью лесовозной дороги раскрытие трещины происходит по всем трем микромеханизмам в силу трехмерного напряженно-деформированного состояния [3]. Раскрытие трещины может происходить при однократном либо циклическом приложении нагрузки.

При однократном приложении постоянно возрастающей нагрузки (при движении транс-

портного средства с нагрузкой на ось выше критической) условия разрушения записываются в виде предельной поверхности:

φ ( K _I, K _II, K _III) = 0. Например,

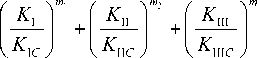
= 1,

где m ₁ , m ₂ , m ₃ , K _{I C}, K _{II C}, K _{III C} – константы материала; K _I, K _II, K _III – коэффициент интенсивности напряжений по соответствующим типам растрескивания [4].

Или в частном случае:

a — + a —+ a — 1,      (3)

123 ^K I C       ^K II C       ^K III C

α1 + α2 + α3 = 1, где α1, α2, α3 – весовые коэффициенты.

При допущении, что раскрытие трещины осуществляется по трем механизмам, коэффициент интенсивности напряжений K_i может быть определен по формуле:

K i = Y ( 1 ^ с^П ,

где σ_i – интенсивность напряжений; Y_i ( l ) – коэффициент, учитывающий размеры покрытия и вид дефекта; l – длина трещины.

Условие разрушения в этом случае запишется в виде:

K_i ≥ K_iC .                    (5)

Зная критический коэффициент интенсивности напряжений К_iC , можно определить вероятность безотказной работы P при предположении, что плотность распределения вязкости разрушения материала дорожной конструкции f ₁ ( K_iC ) и коэффициента интенсивности напряжений f ₂ ( K_i ) известны. Кроме того, предположим их независимость. Тогда искомая функция определится уравнением:

P = Pr { K_iC – K_i ≥ 0}.            (6)

Вероятность того, что коэффициент интенсивности напряжений находится в интервале

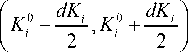
определяется известным равенством:

Pr I K ⁰ — dKL <  K <  K ⁰ + dK I = f (K °) dK . (7) i 2                             2 i                          .

Вероятность того, что вязкость разрушения К_iC превышает некоторое значение коэффициента интенсивности напряжений K_i ⁰ , определится выражением:

да

P = Pr ( K C >  K i ) = J f ( K C ) dK_te .        (8)

_Ki 0

Вероятность того, что значение коэффициента интенсивности напряжений K_i заключено в малом интервале dK_i , а вязкость разрушения K_iC превышает коэффициент интенсивности напряжений, задаваемый этим интервалом, имеет вид:

да f2 ( K, ) dK Д f ( Kc ) dKc.          (9)

K i ⁰

Таким образом, зависимость для оценки вероятности безотказной работы при однократном нагружении путем интегрирования по вязкости разрушения запишется:

+да

iC

P =

J f. ( K c ) J f 2 ( K ) dK- dK c .

-да                -да

В случае, когда величины K_i и K_iC распределены по нормаль н ом у закону, с математическими ожиданиями K, , K -c и дисперсиями D K. , D KC , вероятность безотказной работы P может быть определена по формуле:

2 i да t

P = ^= fe"T dt, v2njz kc - Ki V DKC + DK,

Если величины K и K _C имеют двухпараметрическое распределение Вейбулла, вероятность безотказной работы определяется формулой:

да /    \^a

I x I a

P = 1 -           i - exp

0 V ° i ) x

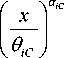
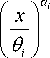
dx , (12)

где α , θ – соответственно параметры формы и масштаба в распределении коэффициента интенсивности напряжений; α _С , θ _С – соответственно параметры формы и масштаба в распределении вязкости разрушения.

Представленные выводы верны для статического нагружения. Критический коэффициент интенсивности напряжений K _C определяется экспериментально при статическом нагружении. На практике имеет большое значение и ударное нагружение. Так, при движении лесовозных автопоездов по дороге, при проезде автомобиля через выступ неровности возникает динамический удар на покрытие на некотором расстоянии за ним, в результате чего нагрузка на покрытие значительно увеличивается. В случае динамического нагружения вычисляется динамический коэффициент интенсивности напряжений К _Д , который сравнивается с критическим значением K _ДС . Параметр K _ДС является характеристикой материала, определяется экспериментально и зависит от скорости нагружения. Вероятностный подход, изложенный выше, может быть полностью применен и для случая динамического нагружения [5].

Оценка надежности дорожного покрытия при воздействии предельной нагрузки с позиции механики разрушения 83

* Работа выполнена при поддержке международного проекта «Новые трансграничные решения в области интенсификации ведения лесного хозяйства и повышения степени использования топливной древесины в энергетике» ППС ЕИСП «Карелия» в рамках реализации Программы стратегического развития ПетрГУ на 2012–2016 гг.