Оценка надежности мультиверсионной программной архитектуры систем управления и обработки информации

Программное обеспечение (ПО) применяется в различных системах управления и обработки информации. В зависимости от приложения данных систем к ПО предъявляются различные требования по надежности. Существует ряд критических систем, отказ которых может нанести урон здоровью и жизни людей, а также привести к экономическим и материальным потерям.

Одним из методов, позволяющих обеспечить высокую надежность и отказоустойчивость программной архитектуры систем управления и обработки информации является мультиверсионное программирование (NVP) [1]. Метод заключается в применении избыточного числа версий программного обеспечения, выполняемых параллельно. Результаты работы версий сравниваются с помощью алгоритма голосования: если большинство версий возвращают одинаковый результат, то он принимается, как результат работы ПО, иначе наступает отказ. Таким образом, с помощью метода мультиверсионного программирования реализуется мультиверсионная программная архитектура, устойчивая к сбоям.

Итак, отказ программного обеспечения наступит при одновременном отказе большинства версий. Под одновременным отказом следует понимать не отказ в один и тот же момент времени, а отказ при обработке одних и тех же данных, т. е. на k-й итерации выполнения. Чем больше время выполнения версии, тем больше вероятность того, что версия откажет.

Цля оценки надежности программного обеспечения необходимо знать интенсивности отказов (X) и время выполнения (h.) каждой версии. Способы определения интенсивности отказа предложены в работе [2], а время выполнения может быть непосредственно измерено. Предполагается, что время выполнения каждой версии постоянно.

Функционирование программного обеспечения с тремя версиями (N = 3) можно продемонстрировать с помощью графа состояний (рис. 1). Номер состояния соответствует числу отказавших версий.

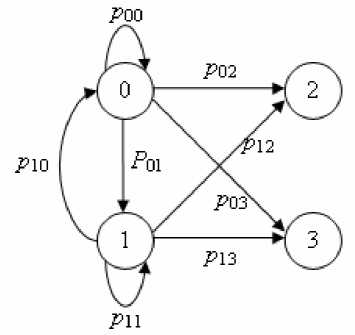
Рис. 1. Граф состояний

В начальный момент времени, что соответствует нулевой итерации, ПО находится в состоянии 0. После первой итерации ПО может остаться в состоянии 0 (все версии вернут верный результат), перейти в состояние 1 (произойдет отказ одной из трех версий), перейти в состояние

2 (отказ двух версий из трех) или в состояние 3 (отказ всех версий), соответствующие переходы показаны на графе. Состояния 2и 3 являются поглощающими и приводят к отказу программного обеспечения.

Так как между поступлением данных на обработку и принятием решения алгоритмом голосования пройдет время h_m = max(h),y = 1,..., N, то переход из одного состояния в другое будет происходить через h_m.

Архитектура ПО представляет собой систему с дискретным числом состояний и дискретным временем. Время между отказамиу-й версии имеет экспоненциальное распределение с параметром X . Как известно, поток событий, имеющий экспоненциальное распределение, обладает свойством отсутствия последействия [3], поэтому для построения модели ПО может быть применена теория марковских цепей [3].

Для нахождения распределения вероятностей состояний на к-й итерации нужно знать начальное распределение вероятностей_р _а (О) и матрицу переходных вероятностей |[р _а6 ||, затем, применяя рекуррентную формулу [3], находятся искомые значения:

N

Pb (k) = Z Pa (k - 1) Pab , a =0

к 1,2, .;Ь = О, 1, ., А. (1)

Формула (1) является частным случаем уравнения Колмогорова-Чепмена. В начальный момент времени система находится в состоянии О, таким образом, начальное распределение вероятностей известно. Для получения матрицы переходных вероятностей необходимо определить все вероятности, указанные на рис. 1.

Версии имеют постоянную интенсивность отказов X., это значит, что поток отказов является стационарным, а, следовательно, вероятность безотказного выполнения любой итерации для каждой версии остается неизменной. Вероятность безотказного выполненияу-й версии pj

—X/ • hi = e j j

Система может попасть в состояние О двумя способами: либо из состояния 1, либо оставшись в состоянии О. Оба перехода возможны только при верном выполнении одновременно трех версий, это значит что

P 0о = P io = r o = P ¹ P 2 P 3 . ⁽³⁾

Вероятность попасть в состояние 1 из состояния О рав на вероятности остаться в состоянии 1, потому что пере ход произойдет при отказе одной из трех версий:

P 10 = P 11 = r i = ^{(1 -} P ¹⁾ P ² P ^{3 +} + P ¹ (1 - p ² ) P ³ + P ¹ P 2 (1 - P 3 ) .

Аналогично определяются вероятности перехода в состояния 2и 3:

P 02 = P 12 = ^r 2 = ^{(1 -} P ^{1)(1 -} P 2 ) P 3 ⁺

+ (1 - p ¹ ) p 2 (1 - p 3 ) + p ¹ (1 - p ² )(1 - p 3 ) ,       ⁽⁵⁾

P 03 = P 13 = ^r 3 = ^{(1 -} P ^{1)(1 -} P ^{2)(1 -} P ³⁾ .         (6)

Матрица переходных вероятностей примет вид:

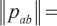
^p 00 ^p 01 ^p 02 ^p 03

Далее, используя формулу (1) и начальное условие, находим вероятности пребывания в каждом состоянии на любой итерации.

При произвольном числе версий (А) изменится вид матрицы переходных вероятностей. В общем случае она имеет вид квадратной матрицы размерности (А+1) (А+1):

II P ab =

(РМ Р ... P»N

Poo Poi • • • ^P«N

0 0 0 1

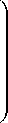
^гд^е P b =

I N

0, if I ^ b , I >  cei

I 2

(N

1, if I = b , I >  cei

,              , I 2

- 1

,

- 1

I N ceil

I 2

- опера-

тор округления до наибольшего целого числа.

Для вычисления остальных вероятностей необходимо воспользоваться рассуждениями к формулам (3)-(6).

Пример. Пусть программное обеспечение имеет три одинаковые по надежности версии (А= 3), время выполнения 5 мин (h = 5), интенсивность отказа - один раз в месяц ( X = 1О мес^-1 или X = О,ООО 2 мин^-1). Рассчитаем надежность ПО через к = 1051 2ОО итераций, что составляет 1О лет работы.

По формуле (2) находится вероятность безотказной работы при выполнении любой итерации:

p = e ^{-X h} = e ^-0'^00(М = 0,999 .

Соответственно вероятность отказа:

q = 1 - p = 1 - 0,999 = 0,001 .

С помощью формул (3)-(6) определяется матрица переходных вероятностей:

1 0,997 0,003 2,997 • 10 ^{- 6} L10 ^{- 9} "

0,997 0,003 2,997 • 10 ^{- 6} L10 ^{- 9}

0       0     10

0        0     11

V7

Затем по формуле (1) находятся вероятности пребывания в каждом состоянии. Вероятность того, что через 1О лет работы ПО останется в работоспособном состоянии составляет О,О4. На рис. 2и 3 представлены графики изменения вероятностей в зависимости от номера итерации.

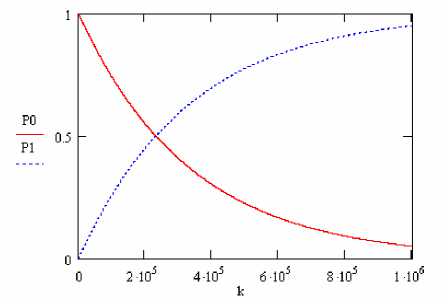
Рис. 2. Изменение вероятности пребывания в работоспособном состоянии (кривая РО) и в состоянии одновременного отказа двух версий (кривая Р1)

Хотя вероятность одновременного отказа трех версий незначительна, это событие следует учитывать, так как с ростом количества итераций вероятность увеличивается, кроме того, она зависит от интенсивностей отказа.

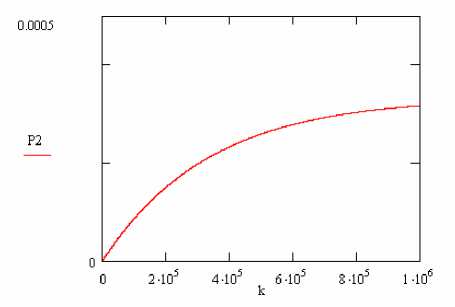
Рис. 3. Изменение вероятности пребывания в состоянии одновременного отказа трех версий

Таким образом, предложенная модель для оценки надежности мультиверсионной программной архитектуры позволяет рассчитать вероятность безотказной работы программного обеспечения систем обработки информации и управления при длительной работе.