Оценка надежности системы ROPS лесозаготовительных машин с применением катастрофы сборки

Теория катастроф как раздел математики начала формироваться еще в середине ХХ века на основе теории особенностей гладких отображений и теории динамических систем. Основоположниками современной теории катастроф являются французский математик Р. Том и российский математик В. И. Арнольд. Катастрофами называются скачкообразные изменения, возникающие в виде внезапного ответа системы на плавное изменение внешних условий.

Одной из семи элементарных катастроф, по Р Тому [8], является катастрофа сборки, потенциальная функция которой определяется

V ab ⁽ x ) = 4 x ⁴ + 2 ax ² + ^b x , ⁽¹⁾

где x – переменная состояния; a , b – переменные управления.

Многообразие M катастрофы задается урав нением

0 = d Vab(x) = x3 + ax + b, dx

которое имеет от одного до трех вещественных корней. Природа этих корней зависит от дискриминанта

Катастрофа происходит, когда дискриминант D меняет знак с отрицательного на положительный [8].

Полагаем, что изменения управляющих переменных являются случайными. В качестве случайных величин или случайных функций [4], [9] можно представить нагрузку, геометрические характеристики, параметры прочности, механические свойства материалов и т. д. Очевидно, что вследствие разброса возможных значений конструкции будут работать с более или менее редкими перегрузками [1]. Поэтому определенный интерес представляет изучение вопросов проектирования элементов конструкций технологических машин с позиций теории катастроф с учетом стохастической природы возмущающих факторов.

В работе А. В. Питухина [3] для оценки вероятности катастрофы сборки предложен метод статистической линеаризации для случая, когда управляющие переменные являются случайными величинами. Тогда оценки математического ожидания и дисперсии дискриминанта D определяются

D = 4a3 + 27b2; (4)

s

2 D

'dD" d a v ⁰

2 s a

+

[d D | Э b

\ 0

s b =

= 144 a -⁴ s 2 + 2916 b² s b ² ,             (5)

где a , b – математические ожидания управляющих переменных; s _a ² , s _b ² – дисперсии управляющих переменных.

С помощью данных зависимостей была получена возможность оценки вероятности безотказной работы элементов конструкций технологических машин и оборудования. Весьма важной является задача оценки энергии деформирования элементов конструкций вплоть до их разрушения, особенно это касается защитных каркасов кабин лесопромышленных тракторов [5], [6].

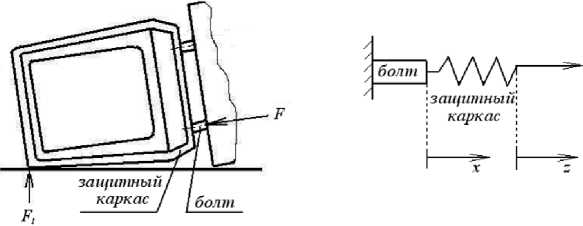
Рис. 1. Cхема нагружения кабины трактора

ПРИМЕР ОЦЕНКИ ВЕРОЯТНОСТИ БЕЗОТКАЗНОЙ РАБОТЫ ЗАЩИТНОГО УСТРОЙСТВА КАБИНЫ ТРАКТОРА

Представим сопротивление стержня растяжению в виде зависимости:

F(x) = A₂·x – C₂·x³ , (6) где F(x) – нагрузка; x – абсолютная деформация стержня; A₂ , C₂ – эмпирические коэффициенты.

Полная диаграмма растяжения стержня, описываемая зависимостью (6), представлена на рис. 2. Такие полные диаграммы деформирования (с падающей ветвью) могут быть получены на испытательных установках с большой жесткостью.

Рассмотрим случай бокового нагружения кабины, имитирующего опрокидывание колесного лесопромышленного трактора (скиддера) ТЛК-4-01. Согласно требованиям ГОСТ Р ИСО 8082-1-2012, самоходные машины для леса должны оборудоваться устройствами защиты при опрокидывании (ROPS – roll-over protective structures), снижающими риск нанесения травм оператору в случае возникновения аварийной ситуации путем поглощения энергии деформирования элементов [6]. В нашем случае система ROPS представляет собой замкнутый защитный каркас (пояс), расположенный в поперечной плоскости симметрии кабины и имеющий две болтовых опоры крепления к раме трактора. В случае возникновения аварийной ситуации основные нагрузки будут восприниматься защитным каркасом и болтом его крепления к несущей раме (рис. 1). Система ROPS при этом до л ж н а поглотить энергию деформации не менее

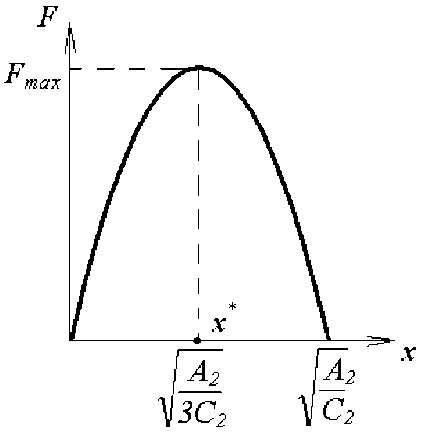
Рис. 2. Полная диаграмма деформирования стержня

US

1,25

где m – масса машины, m = 14500 кг. Тогда

U S

Вариант 1 (в качестве переменной состояния x – абсолютная деформация болта крепления).

Защитный каркас заменим эквивалентной пружиной с жесткостью А₁ и деформирующей силой F . Болт представим в виде стержня, в процессе растяжения испытывающего упругопластические деформации. Таким образом, получаем условную схему нагружения, энергетически эквивалентную исходной (см. рис. 1).

Полная потенциальная энергия системы складывается из энергий деформирования эквивалентной пружины (ROPS) и стержня (болта)

U = U_ROPS + U_б .

Энергия деформирования ROPS где P – сила сопротивления деформации эквивалентной пружины с жесткостью А1, P = A1·(z – x); z – полная деформация.

Энергия деформирования стержня (болта)

U₆ = f F ( x ) dx = Xf Ax - Cx³ )dx = A 2 x 2- - C i x ⁴ .

á ₀₀22   ₂₄

Следовательно, полная энергия

1                Ax ² Cx ⁴

U = 2 Л1(z - x)(z - x) + 22---24 , после преобразований

U — — Cx. + ⁽ A 1 ^{+ А} ) x² - ^xz + A z ² . 4          2¹2

Отсюда dU        3

--— —Cx + ( A + А ) x — А z .

dx    2     12     1

Полученное выражение аналогично выражению (1), описывающему катастрофу сборки. Поверхность равновесия М определяется уравнением производной dV_ab(x)/dx (2), коэффициенты в котором определяются:

a — —

A t+ J l

C 2

b — ^ .

^C 2 ^.

получим A₂ = 26500 Н/мм, C₂ = 22,1 Н/мм³.

Значения А 1 , А 2 и С 2 полагаем случайными величинами с математическими ожиданиями, подсчитанными выше. Таким образом, численные значени я задаем в следую щ ем виде [7]:

A 2 = 26500 Н/мм, C 2 = 22,1 Н/мм³,

σ _A2 = 2650 Н/мм,

σ _C2 = 2,21 Н/мм³, σ _А1 = 0,1· À 1 .

Оценка критических значений нагрузки и энергии деформирования.

Определим критические значения нагрузки и энергии деформирования при условии монотонного увеличения z от 0 до наступления катастрофы. Значение переменной b , соответствующее скачку, определим из условия D = 0 с учетом зависимостей (3) и (7)

Допустим, что A 1 , А 2 , С₂, z - случайные величины с математическими ожиданиями A 1 , А ₂ , С ₂ , z и дисперсиями s A 1 , s А ₂ , s ^ ₂ , s 2 . Согласно методу статистической линеаризации

a — —

^A 1 ^{+ А} 2 ; s a

C 2

— c2

sA 1 + sA2 +

^A 1 ^{+ A} 2

C 2

2   2

s ^{C 2} ; (9)

Критическое значение полной деформации получим с использованием зависимостей (8) и (11)

b — A1z

^C 2 ^;

sb

Численное решение задачи целесообразно

осуществить в следующем порядке: определить жесткость А₁ эквивалентной пружины, оценить коэффициенты A 2 и C₂ в полной диаграмме деформирования (6), задать значения средних квадратических отклонений коэффициентов A₁ , А₂ и С₂ .

Численное значение жесткости А 1 эквивалентной пружины целесообразно определять методом конечных элементов. В работе [3] расчет был произведен с использованием пакета прикладных программ «Зенит».

Определим коэффициенты А₂ и С₂ в полной диаграмме растяжения стержня. Для этого пересчитаем F_max и x^* для стержня, моделирующего болт, через предел прочности a B и относительное удлинение d соответствующей стали.

Для стали 30, согласно справочным материалам, a B = 500 МПа, 5 = 20 %. При диаметре стержня d = 30 мм и длине l = 100 мм максимальная

Учитывая, что a = - 3x_C² [10], определим абсолютную деформацию, соответствующую разрушению защитного устройства

xc

I A1 + А ₂

Тогда критическая нагрузка с учетом (6) и (13)

Fc — A2 ■ xc — C2 ■ x3

I A1 + А 2

и критическая энергия деформирования с учетом (12) – (14)

I    ( A 1 + ^А 2 ) 2 [ (2 A 2 — ^А 1 ) ²    5 A 2 — А 1

. (15)

разрушающая стержень нагрузка и соответствующее ей абсолютное удлинение определятся:

p d2

max 4

S B — 353000 Н; x* — l ■ ^ — 20 мм.

Подставляя численные значения F_max и x^* и решая систему уравнений

x

р — Ах* - С х* 3 .² max ^{— A} 2 ^{x   C} 2 ^x ,

Вариант 2 (в качестве переменной состояния x – абсолютная деформация ROPS).

Как отмечается в ГОСТ Р ИСО 8082-1-2012, боковое нагружение ROPS с боль шо й вероятностью приводит к появлению остаточных деформаций. В связи с этим представляет определенный интерес исследование защитных свойств пояса безопасности с учетом его пластических деформаций.

Систему ROPS п р едставим в виде бруса, который в случае возникновения аварийной ситуации будет испытывать упруго-пластические деформации (рис. 3).

Полная потенциальная энергия для данного варианта запишется в виде

A lx

U = U₆. + U ROPS = J P ( ^A l ) d ^A l ⁺ J FA x ) dx ,

II _ ( A + ^А 2 ) ^c 6 ■ C 1

'(2 Ai — А2 )2 + 5A — A' 9 А2

ч

. (16)

где P(Al), Al - сила сопротивления деформации и абсолютное удлинение стержня; F(x), x - сила сопротивления и абсолютная деформация ROPS.

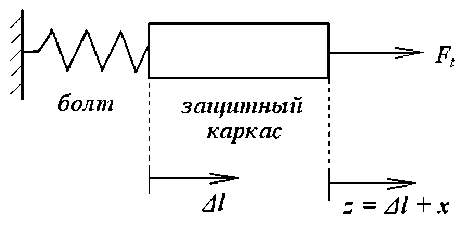
Рис. 3. Эквивалентная схема нагружения с учетом пластических деформаций ROPS

Результаты расчета энергии деформирования по формулам (15) и (16) представлены на рис. 4. Таким образом, расчет системы R OPS без учета пластического течения материала позволяет удовлетворить требованиям ГОСТ только при небольших значениях жесткости.

Тогда

A l                                 x

U = J (A2Al — C2Al3 )dAl + J (A1 x + C1 x3 )dx =

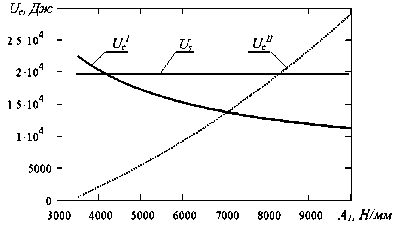
Рис. 4. Графики зависимости критической энергии деформирования от жесткости ROPS: U^ - вариант 1;

U_c ^II – вариант 2; U_s – нормативное значение

A2A l2   C2A l4   A1 x2   C1 x4

Второй член в полученном выражении можно не учитывать ввиду незначительности его величины. Коэффициенты А 1 и С 1 определяются по диаграмме деформирования ROPS, построенной по аналогии с диаграммой деформирования стержня (представлена на рис. 2) при допущении достижения ROPS зоны DLV (DLV - deflection limiting vol u me - зона, соответствующая предельной деформации) при критической нагрузке F_max = 116 кН [5].

^таОтсюда с учетом z = x + Al

C^x4 (A + A2)x2          A zzU —1+             a zx + 2

4          2          2        2

Оценка вероятности безотказной работы.

Оценим математическое ожидание и дисперсию поглощенной энергии с помощью метода статистической линеаризации

Uc — sUc —

(Ai + A2)   (2 Ai  A2)

6 ■ C1

9 À ₂

+

5 A 1 — A ₂

; (17)

и

dU dx

— —C i x ³ + ( A i + A 2 ) x — A 2 z .

avc.

(aUc. a c

s

Вероятность безотказной работы представим как вероятность того, что величина энергии деформирования превысит нормативное значение U_S , регламентированное стандартом

R = Pr{U > U S } = Pr(U_c - U S > 0).

Согласно ГОСТ Р ИСО 8082-1-2012, для ТЛК-4-01 нормативное значение энергии деформирования составляет U_S = 19,8 кДж.

Очевидно, что вероятность отказа

Полученные выражения также соответствуют выражениям (1) и (2), описывающим катастрофу сборки с переменными управления

A + А₂

a —--¹-----

C 1      ^;

b — ^A 2 z ,

C1 , но в качестве переменной состояния x в данном случае выступает абсолютная деформация ROPS.

Критическая энергия деформирования (по аналогии с (15))

q = 1 - r = 1 - Pr(U_c - U S > 0).      (19)

В предположении, что энергия деформирова- ния подчиняется нормальному закону, вероятность отказа может быть выражена

Q = 2 - ф (y) , где Ф(у) - функция Лапласа, Ф(y) — y t2

Г e ~² dt

V2PJ

[2]; у - характеристика безопасности, g —

U c — U S

I s Uc ⁺ s Us

.

Поскольку нормативное значение U S задается, как правило, в виде детерминированной величины, то в зависимости (21) можно положить s Us = 0 и U S = U_S . Тогда для варианта, учитывающего пластические деформации ROPS, при расчетных оценках по формулам (17) и (18) U c = 25,96 кДж и a _Uc = 5,9 кДж характеристика безопасности составит γ = 1,029 ( Ф(γ) = 0,349 [2]), что соответствует вероятности отказа

Q = 0,5 – 0,349 = 0,151.

Рассмотренный пример иллюстрирует возможность применения теории катастроф для оценки вероятности безотказной работы элементов конструкций технологических машин и оборудования при проектировании. Предложенный подход позволяет провести статистический анализ положений равновесия вблизи критических точек, что важно для практических целей.

* Работа выполнена при поддержке Программы стратегического развития ПетрГУ на 2012–2016 гг.