Оценка надежности верификации автографа на основе искусственных нейронных сетей, сетей многомерных функционалов Байеса и сетей квадратичных форм

На сегодняшний день подавляющее большинство офисных документов создается с помощью информационных технологий, для обеспечения аутентичности и целостности которых используется электронноцифровая подпись (ЭЦП). Существенным недостатком классической ЭЦП является то, что она является отчуждаемой от своего владельца в отличие от традиционной подписи. Это обстоятельство является причиной множества компьютерных преступлений. По данным PricewaterhouseCoopers (PwC), число инцидентов, связанных с нарушением информационной безопасности, неуклонно растет [1]: в 2009 году PwC зафиксировано 3,4 млн. инцидентов, в 2010 – 9,4 млн., в 2011 – 22,7 млн., в 2012 – 24,9 млн., в 2013 – 28,9 млн., в 2014 – 42,8 млн., в 2015 – 59 млн. Оценки среднего ущерба от одного инцидента ИБ зависят от масштаба бизнеса и составляют от 0,41 до 5,9 млн. долларов США. Большая часть убытков обусловлена деятельностью собственных или бывших сотрудников компаний. На сегодняшний день наиболее опасный злоумышленник – это квалифицированный «инсайдер», получивший доступ к ЭЦП руководителя с помощью привилегий своего положения в компании. Чтобы устранить данный недостаток ЭЦП, предлагается перейти к концепции гибридного документооборота, сформулированной в [2]. Ключевым атрибутом гибридного документа является ЭЦП, при формировании которой используются биометрические данные ее владельца. В качестве биометрических характеристик (признаков) могут быть использованы параметры воспроизведения и внешнего вида рукописных образов. В настоящей работе проведена оценка эффективности различных преобразователей биометрия–код для решения задачи генерации ключевых последовательностей бит на основе особенностей автографа.

Общая концепция преобразователя биометрия–код

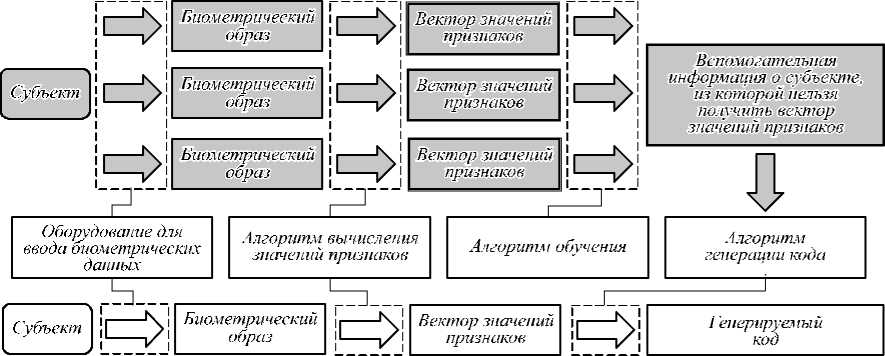
Основное отличие преобразователей биометрия– код (ПБК) от методов обычной биометрической аутентификации состоит в том, что каждый образец биометрических данных предварительно преобразуется в битовую (ключевую) последовательность, которую возможно использовать в целях аутентификации субъекта или криптографической защиты документов (в качестве кода доступа, ключа шифрования и т.д.). При этом эталон субъекта должен храниться в виде вспомогательной информации, не позволяющей восстановить из нее биометрические характеристики субъекта (рис. 1). Требования к защите биометрического эталона при разработке систем высоконадежной биометрической аутентификации прописаны в ГОСТ Р 52633.0-2006 [3] (пункты 5.2–5.3 стандарта). Если генерируется н ехаракт ерный для субъекта код, происходит ошибка 1-го рода. За ошибку 2-го рода принимается ситуация, при которой коды, полученные из биометрических данных двух различных субъектов, совпадают. Вероятности ошибок 1-го (FRR, false reject rate ) и 2-го (FAR, false acceptance rate ) рода характеризуют надежность ПБК. При верификации кода решение принимается исходя из допустимого расстояния Хемминга H межд у генерируемым и верным кодами.

Биометрические признаки

Сформирована база данных автографов 65 субъектов, для ввода которых испытуемые пользовались графическим планшетом Wacom. Подпись состоит из функций положения пера на планшете x(t), y(t) и давления пера на планшет p(t), где t – это время в дискретной форме. Операция преобразования образца и получения из него вектора значений признака (реализации) в настоящей работе реализуется аналогично тому, как это выполнялось в работе [4]. Краткое описание признаков представлено в табл. 1. Общее количество признаков – 236. Предварительно, перед вычислением значений признаков, функции x(t), y(t) и p(t) нормируются по дли- тельности. Выполняется прямое разложение функций в ряд Фурье и последующее обратное преобразование, но с одинаковой длительностью, равной средней длине масштабируемых сигналов (размерность на выходе должна быть числом, кратным степени 2).

Формирование вспомогательной информации о субъекте

Генерация битовой последовательности

Рис. 1. Общая схема преобразователя биометрия–код

Табл. 1. Признаки, используемые для генерации кодов в настоящем исследовании

№	Краткое описание признаков	Количество признаков
1	Расстояния между 16 точками подписи, нормированные по длине подписи, в трехмерном пространстве (третье измерение – это давление p ( t )). Точки выбираются равномерно, далее находятся расстояния между всеми различными парами этих точек [4].	120
2	Следующие характеристики статического изображения подписи: отношение длины подписи к её ширине, центр подписи, угол наклона подписи, угол наклона между центрами половин подписи [4].	5
3	Нормированные по энергии амплитуды первых 16 (наиболее низкочастотных) гармоник функции скорости перемещения пера на планшете v xy ( t ) и функции давления пера на планшет p ( t ). Первые 16 гармоник содержат более 95% энергии сигналов v xy ( t ) и p ( t ), что характерно для всех испытуемых [4].	32
4	Коэффициенты корреляции между всеми парами функций подписи x ( t ) , y ( t ) , p ( t ) и их производными x’ ( t ) , y’ ( t ) , p’ ( t ) [4].	15
5.	Значения функций x ( t ), y ( t ) и p ( t ), а также функции скорости перемещения пера на планшете v xy ( t ), которые выбираются равномерно (используется по 16 значений каждой функции) [4].	64

Модели преобразователей биометрия–код

Изначально сложилось 2 основных подхода к реализации преобразователей биометрия–код: «нечеткий экстрактор» [5] и нейросетевой (НПБК). Первый основан на квантовании «сырых», необогащенных значений признаков и применении к ним алгоритмов помехоустойчивого кодирования для исправления ошибок, возникающих вследствие невозможности точного повторного воспроизведения биометрического образа. По результатам исследований и экспериментального сравнения данных подходов установлено, что нечеткие экстракторы на основе классических самокорректирующихся кодов существенно уступают нейронным сетям в надежности генерации ключевых последовательностей, а также обладают множеством недостатков [4, 6–7]. Поэтому в настоящем исследовании «нечеткие экстракторы» не рассматриваются в качестве варианта решения поставленной задачи.

Второй подход основан на идее использования искусственных нейронных сетей . На данный момент эта идея доведена до эффективных практических решений. Сеть искусственных нейронов обогащает реализации , после чего эти данные квантуются на выходе сети. Корпораци ей Google и рядом иных производителей используются так называемые «глубокие» нейронные сети Галушкина–Хинтона. Предложил многослойные нейронные сети и алгоритм их обучения в 1974 году А.И. Галушкин [8]. Джефри Хинтон [9] усовершенствовал алгоритм об учения, применив машины Больцмана для обучения нижних слов нейронов. Попытки использования «глубоких» нейронных сетей к решению задачи идентификации личности человека по динамике воспроизведения автографа не дают желаемого эффекта [10], так как у «глубоких» нейронных сетей существует ряд принципиальных недостатков:

• -    алгоритм обучения (переобучения) «глубоких» нейронных сетей «обратным распространением ошибки» имеет экспоненциальную вычислительную сложность, его нельзя реализовать на планшетном компьютере, оторванном от обучающих серверов корпорации Google (что неприемлемо в приложения х биометрический аутентификации);

• -    указанный алгоритм обучения (переобучения) «глубоких» нейронных сетей треб ует наличия огромной базы (порядка 100 000 и более) обучающих примеров;

• -    современные «глубокие» нейронные сети имеют до 100 слоев нейронов, что является избыточным по теоремам Колмогорова [11];

• -    пользователи «глубоких» нейронных сетей не могут быть уверены в надежности их работы, так как для них отсутствуют методы быстрого тестирования вероятностей ошибок первого и второго рода (по этой причине разработчикам этой технологии приходится прид умывать другие критерии оценки надежности сетей);

• -    обучение глубоких нейронных сетей не может быть полностью автоматизировано и всегда ведется под контролем человека, что нежелательно в ответственных приложениях информационной безопасности.

В настоящем исследовании принято решение отказаться от использования «глубоких» нейронных сетей в рамках поставленных задач, так как этот путь треб ует огромных затрат вычислительных ресурсов и опасен для пользователей (нельзя компрометировать биометрические данные субъекта, оправляя их на удаленный сервер). Далее в ст атье рассматриваются «широкие» нейронные сети и их модификации, использование которых в приложениях биометрической аутентификации является рекоменд уемым подходом в России. Данный подход хорошо стандартизован (гораздо лучше, чем «нечеткие экстракторы», семейство ГОСТ Р 52633 насчитывает 8 стандартов, описывающих требования к процедурам быстрого обучения, тестирования НПБК и интерфейсы взаимодействия с ними). Дополнительным преимуществом подхода является отсутствие привязки к огромной базе подписей, коллективно созданной для обучения и тестирования нейронных сетей.

В ГОСТ Р 52633.5-2011 [12] описан первый не итерационный абсолютно устойчивый алгоритм обучения сети персептронов, разработанный для биометрии. В соответствии с ГОСТ Р 52633.5-2011 [12] рекомендуется использовать однослойные или двухслойные нейронные сети, большее количество слоев считается избыточным [6]. Первый слой обогащает биометрические данные, второй слой играет роль кодов, исправляющих ошибки [12]. Сравнение сетей различны х функционалов целесообразно производить без использования второго слоя, в настоящей работе буд ут применяться только однослойные сети. Разница межд у свёрточными сетями (сетями глубокого обучения Галушкина–Хинтона) и «широкой»

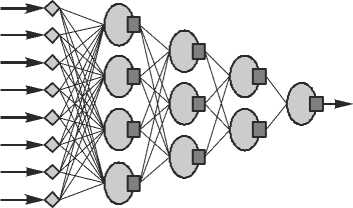
нейронной сетью, обученной по ГОСТ Р 52633.5, иллюстрируется на рис. 2.

• б)

Рис. 2. Два типа архитектуры нейронных сетей: «глубокие» и «широкие» нейронные сети: глубокая сеть нейронов Галушкина–Хинтона (а) и широкая сеть нейронов по ГОСТ Р 52633.5-2011 (б)

Согласно ГОСТ Р 52633.5-2011 для обучения персептронов треб уется не менее 21 реализации образа «Свой» и 64 независимых реализации образа «Чужой». Для каждого субъекта треб уется создавать отдельную сеть нейронов. Операции по настройке сети описаны в стандарте [12], а также их можно найти в работах [4, 6–7]. Отметим лишь, что модули весов нейронов первого слоя вычисляются по формуле (1), а выход сумматора нейрона на этапе верификации определяется по формуле (2).

µ j = |M ч 〈 a j 〉 – M с 〈 a j 〉 | / σ ч 〈 a j 〉 ∙σ с 〈 a j 〉 ,                   (1)

где M с 〈 a j 〉 – математическое ожидание значений j -го признака образа «Свой», σ с 〈 a j 〉 – среднеквадратичное отклонение значений j -го признака образа «Свой», M ч 〈 a j 〉 и σ ч 〈 a j 〉 – аналогичные показатели образа «Чужой». Если нейрон настроен на выдач у единицы при поступлении реализации образа «Свой», то знак весового коэффициента выбирается исходя из правила: «+» при M ч 〈 a j 〉 < M с 〈 a j 〉 , иначе «–». Если нейрон настроен на нуль, знаки инвертируются.

• У, = Е Н у ' a j + И о ,                                 (2)

j = 1

где a j – значение j -го входа i -го нейрона, ассоциированного с одним из признаков, m – число входов нейрона, µ j – весовой коэффициент j -го входа i -го нейрона, µ 0 – нулевой вес, отвечающий за переключатель квантователя нейрона (пороговое значение).

Помимо сетей персептронов, для генерации кода можно использовать сеть иных функционалов, в частности, квадратичных форм (3). Классическая квадратичная форма предполагает обращение корреляционных (ковариационных) матриц (размерность матрицы равна количеству признаков). В биометрических приложениях обращение этих матриц затруднительно, если их размерность оказывается высокой [13-14]. В этом случае возникает эффект, называемый «проклятием размерности» [13-14]. Поэтому возможно использовать сети малоразмерны х квадратичных форм (3) или высокоразмерных квадратичных форм, не учитывающих корреляционные связи, например, сеть из функционалов Пирсона (4) [13-15]. Метрика Пирсона (4) не учитывает корреляцию между признаками, с усилением корреляционной зависимости ее мощность снижается [15]. Альтернативным вариантом является мера Байеса-Пирсона (5) [15], которая зависит от многомерной корреляции межд у признаками. Механизм влияния корреляционных связей на метрику (5) поясняется в работе [15].

y ( a ) = (M { a ) - a ) T • [ R ] ¹ • (M( a ) - a ),            (3)

где a - вектор значений признаков с единичными стандартными отклонениями, M { a j - математическое ожидание нормированных значений соответствующих признаков.

™ (M ( a j ) - a )² y - = X—, j = 1 c< a j)

mm y- = XX| j =1 k=1

^|M < a k ^)- a k | ^|M < a j^ ^{- a}j ¹

-

σ〈ak〉          σ〈aj〉

I,

где a j - значение j -го входа - -го нейрона, ассоциированного с одним из признаков, M ( a j ) - математическое ожидание значений j -го входа - -го нейрона, о { a j ) - среднеквадратичное отклонение значений j -го входа - -го нейрона, m - количество входов нейрона.

В работах [14, 16] предложено использовать сеть многомерных функционалов Байеса (6) [16], которые так же, как мера Байеса-Пирсона, ориентированы на нахождение близости входного образа не только к эталону, но и к корреляционным связям образа межд у признаками. В теории m -мерный вычислительный элемент Байеса (6) работает лучше при повышении размерности m и значений модулей коэффициентов его равной коррелированности [16].

m yk ,j = Xi

I = 1

^IM < ^ak ^{) - a}k , j ^{1 IM} < a - ^{) -} a - , j ¹

-

σ〈ak〉

σ〈ai 〉

I,

где a , - значение - -го признака (входа нейрона) с высоким значением модуля корреляции | n,k | по отношению к k -му биометрическому признаку a kj ( - ^ k ), j -номер биометрического образца образа «Свой», для которого вычисляется функционал, M ( a - ) и о ( a - ) -математическое ожидание и среднеквадратичное отклонение - -го признака (входа нейрона). При функциональной зависимости признаков (| r |=1) значение

метрики (6) всегда имеет нулевое значение. При уменьшении | r | значения функционала (6) и их стандартное отклонение возрастают.

При формировании сети функционалов (4) и (5) обработчики признаков соединялись с нейронами случайным образом. Количество нейронов N и входов m задавалось как параметр и изменялось в процессе вычислительного эксперимента. Сеть многомерных функционалов Байеса (6) формировалась иным образом. Изначально вычислялись коэффициенты парной корреляции r между всеми сечениями (совокупностями значений) всех признаков (рис. 3) обучающей выборки. Признаки соединялись с входами нейронов исходя из модуля равной коррелированности, под которой подразумевается, что разница | r | для признаков не превышает т (значение т задавалось как параметр). Сначала формируется K 1 нейронов для первого признака, потом K 2 для второго и так далее. С первым из K 1 нейронов соединяются первый признак и признаки, которые имеют модуль коэффициента корреляции с ним в интервале [1; 1- Т ], если их число не менее двух (минимальная размерность). Далее производится поиск признаков, имеющих модуль коэффициента корреляции с первым признаком в интервале [1- т , 1-2 Т процедура повторяется многократно, пока 1- l • т > ф , где ф -максимальный модуль корреляции учитываемых признаков, l - номер итерации поиска признаков с равной корреляцией. Аналогичным образом формируются по K j нейронов на признак, с каждым из которых связан j -й признак и - -е признаки, если 1-( 1 -1) т < | r-- j |<1- l •т . Общее количество нейронов сети равно сумме коэффициентов K j , т.е. число нейронов для каждой сети (для каждого из испытуемых) не является фиксированным, как и количество входов нейронов.

Независимо от типа нейрона, значение на выходе его функционала сравнивается с пороговым. Для каждого нейрона существует оптимальный порог срабатывания, который вычисляется (кроме персептронов) исходя из произведения 6 = y max • h , где y max - это максимальное значение функционала при поступлении на вход обучающих реализаций образа «Свой», h - стабилизирующий коэффициент, экспериментально подбираемый для каждого пространства признаков по минимальной сумме вероятностей ошибок 1-го и 2-го рода. Если порог превышен, нейрон выдает единицу («1»), иначе нуль («0»). Настройка сети на нужный выходной код производится инвертированием выходных значений отдельных нейронов. Название искусственной нейронной сети зависит от метрики, которая лежит в ее основе: Пирсона-Хемминга (4), Байеса-Пирсона-Хемминга (5), Байеса-Хемминга (6).

Особенностью функционалов (4), (5), (6) является необходимость хранения параметров распределения признаков. Н едостаток устраняется путем создания гибридной сети с изолированным потоком персептронов (2), на выходах которых буд ут шифроваться параметры нейронов иных функц ионалов по принципу защищенного нейросетевого контейнера [4].

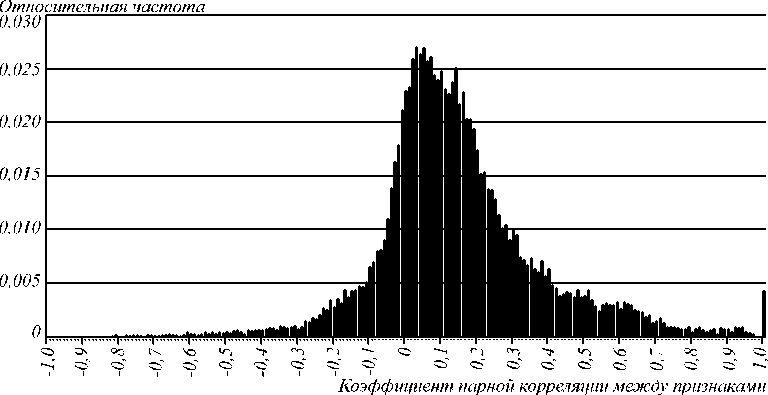
Рис. 3. Корреляционная зависимость 236 признаков подписей для 65 испытуемых (вычисление коэффициентов корреляции выполнялось в отдельности для каждого субъекта)

Результаты по генерации кодов и их анализ

Проведен вычислительный эксперимент. Подписи были преобразованы в реализации. Для обучения использовалось по 21 реализации образа «Свой» (а также по 1 реализации каждого образа для обучения персептронов на данны х «Чужой»). Далее проводились серии опытов по верификации субъектов сетями персептронов, Байеса–Пирсона–Хемминга, Пирсона– Хемминга и Байеса–Хемминга. В процессе эксперимента изменялись значения параметров N, m, τ и φ .

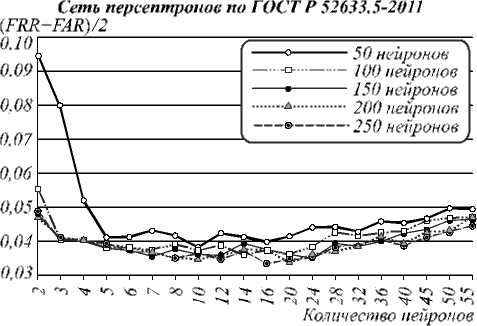
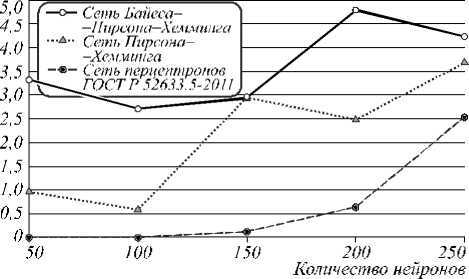
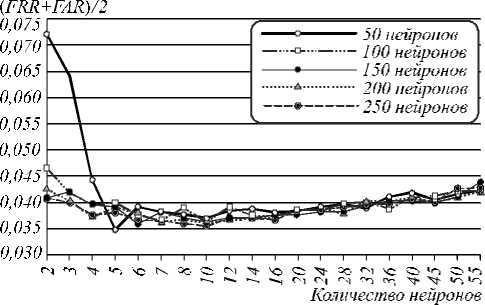
Подсчитывалось общее число ошибок 1-го и 2-го рода, FRR и FAR вычислялись как отношения количества ошибок соответствующего рода к числу проведенных опытов с использованием соответственно реализаций «Свой» и «Чужой». Рис. 4 демонстрирует графики вероятностей ошибки верификации любого рода испытуемых при оптимальных значениях порога (определяется по минимуму FRR+FAR в каждой серии испытаний).

Сет ь Пирсона-Хемминга

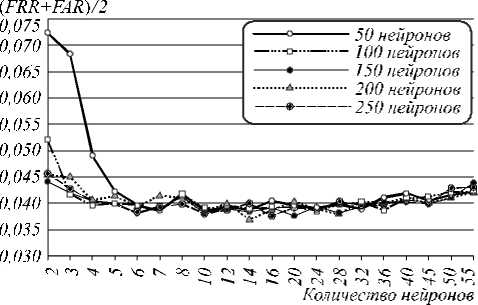
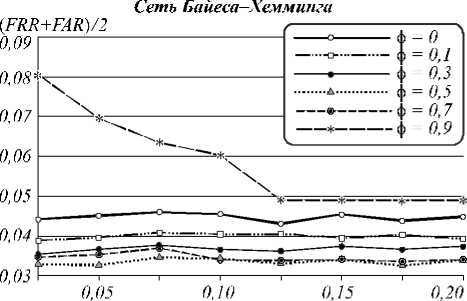
Рис. 4. Вероятности ошибок верификации 65 испытуемых (при пороге H = 0)

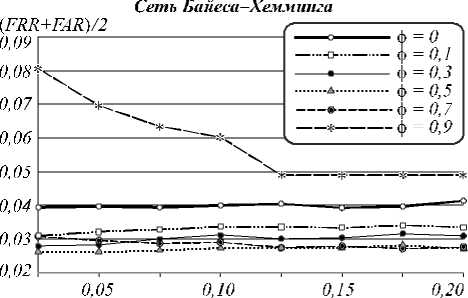
Сет ь Ба йееи-Пиреоиа—Хемминга

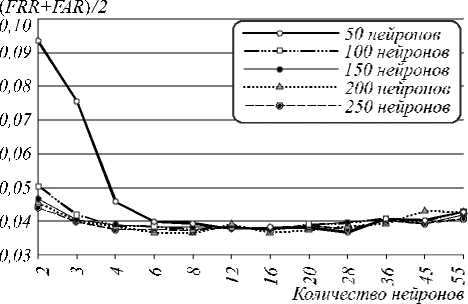
При использовании только «плохих», сильно коррелирующих признаков (0,5 <ф <0,9) вероятность ошибки генерации сетями Байеса–Хемминга (рис. 4) ниже, чем в случае, если использовать также признаки со слабой корреляцией ( ф <0,5). Это подтверждает тезис о том, что многомерный функционал Байеса работает тем лучше, чем выше корреляция между признаками (при работе с «хорошими» признаками функционал с большей вероятностью выдает неверный бит кода). Число признаков с высокой корреляцией невелико (рис. 3), поэтому при ф =0,9 размерность сети низкая и ошибок много, но при увеличении значения т их количество интенсивно снижается. В остальных случаях этот параметр влияет на вероятность ошибок незначительно. С ростом значения т интервал равной корреляции расширяется, т.е. в один функционал попадают признаки со все более различной взаимной корреляцией. Одновременно с этим размерность функционалов m повышается. Это не противоречит тезису о том, что многомерный функционал Байеса повышает работоспособность при увеличении размерности, если признаки равно коррелированы, т.е. снижение вероятности может не происходить по причине неравной корреляции. Однако при ф = 0,9 почти все признаки коррелируют одинаково, т.к. т не может превысить 0,1 (при ф = 0,9, т >0,1 ничего не меняется, рис. 4).

Из рис. 4 видно, что повышение размерности функционалов снижает вероятность ошибок до определенного момента – участка насыщения. Увеличение N не влияет существенным образом на вероятность ошибки, если не корректировать коды, генерируемые сетью. Корректировка ключевой последовательности может быть осуществлена вторым слоем нейронов, реализованным по ГОСТ Р 52633.5-2011 [12], или методом помехоустойчивого кодирования, предложенным в [17] и разработанным специально для биомет- рии. Второй вариант предпочтительнее, т.к. позволяет скорректировать фиксированное количество бит кода.

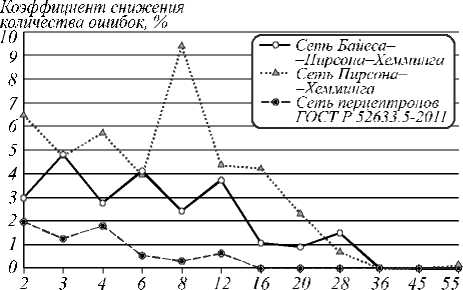
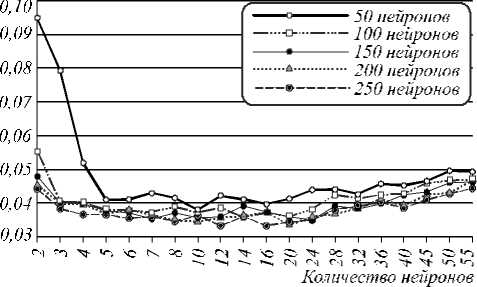
Рис. 5 иллюстрирует след ующее: если повысить пороговое значение расстояния Хемминга H от генерируемого до верного кода, то можно получить выигрыш по сумме FRR+FAR. Как раз это и позволяет сделать метод помехоустойчивого кодирования из [17] без необходимости в хранении эталонного (верного) кода, на который настраивается сеть, для вычисления H . После анализа результатов эксперимента были найдены оптимальные пороговые значения H , при которых сумма ошибок 1-го и 2-го рода была минимальной. Уменьшение ошибок может достигаться, пока корреляция выходных значений нейронов невысока. В этом отношении разные сети имеют отличия (рис. 6). Наиболее показательными являются результаты верификации сетями Бай еса–Хемминга, даже с учетом, что при ф = 0,9 вероятность ошибки не меняется (рис. 4 и 7).

Полученны е результаты (табл. 2) могут быть улучшены при добавлении множества менее информативных признаков (коэффициенты корреляции межд у коэффициентами одно-, двух- и трехмерного ряда Фурье, вейвлет-преобразований, двумерны е и трехмерные амплитуды гармоник суперпозиций функц ий x ( t ) y ( t ), p ( t )). Рассмотренная система из 236 признаков имеет максимум по r (при r = 0,0, рис. 3). В интервал [0; 0,3] попадает около 50 % признаков, их след ует анализировать сетями Пирсона–Хэмминга, более 30% признаков имеют модуль корреляции в интервале [0,3; 0,7], их след ует обрабатывать персептронами, обученными по ГОСТ Р 52633.5. Порядка 30 % признаков с I r I > 0,5 нужно обрабатывать сетями многомерных ф ункционалов Байеса–Хэмминга. Создав гибридную сеть, можно снизить FRR и FAR.

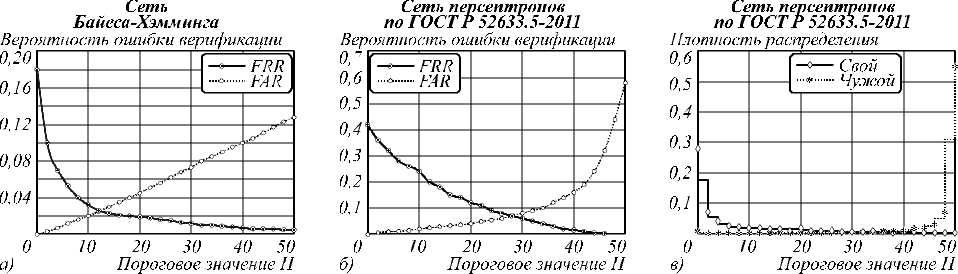
Рис. 5. Влияние H на FRR и FAR (а, б), распределение H от получаемого до верного кода (в)

Табл. 2. Наилучшие полученные параметры надежности верификации субъектов (∆Er – коэффициент снижения суммы вероятностей ошибок FRR+FAR)

Тип сети	FRR, H = 0	FAR, H = 0	Параметры сети, H = 0	FRR, H > 0	FAR, H > 0	Параметры сети, H > 0	Среднее ∆Er , %
Байеса–Пирсона–Хемминга	0,0421	0,0308	m =8; N =200	0,0407	0,029	m =4; N =250	2,08 %
Пирсона–Хемминга	0,0317	0,0421	m = 14; N =200	0,0236	0,0459	m =5; N =50	3,59 %
НПБК ГОСТ Р 52633.5-2011	0,0307	0,0361	m = 16; N =250	0,0307	0,0361	m = 16; N =250	0,6 %
Байеса–Хемминга	0,034	0,0312	т =0,05; ф = 0,5	0,0288	0,0232	т =0,05; ф = 0,5	12,38 %

Коэффициент снижения количества ошибок, "о

Количество входов нейронов (размерность)

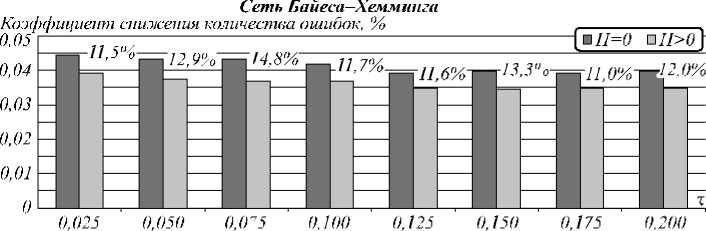
Рис. 6. Снижение вероятностей ошибок верификации с повышением порогового значения H

Сеть персептронов по ГОСТ Р 52633,5-2011 (FRR-E4RV2

Сеть Пирсона—Хемминга

Т

Сеть Байеса—Пирсона—Хемминга

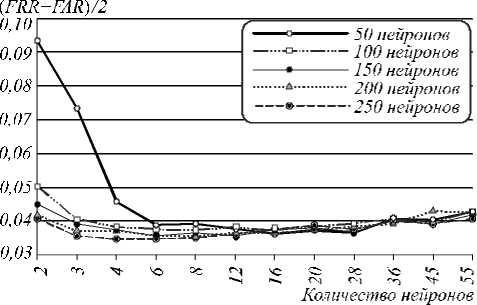
Рис. 7. Вероятности ошибок верификации 65 испытуемых (при пороге H>0)

Заключение

Сформулируем ключевые выводы. В процессе работы экспериментально подтверждено, что многомерный ф унк ционал Байеса работает тем лучше, чем выше коэффициент равной коррелированности при- знаков и выше его размерность. Повышение размерности функционалов позволяет снизить вероятность ошибок до попадания на участок насыщения, дальнейшее повышение размерности не дает преимуществ. Сформировав сеть из нескольких решающих правил с близкими вероятностями ошибок и объединив их результаты, удается получить существенный выигрыш в показателях интегральной ошибки распознавания субъектов. Наивысшим потенциалом по снижению ошибок таким способом обладает сеть Байеса–Хемминга, наименьшим – сеть персептронов (12,38 %). При генерации кода на основе биометрических данных аналогичного эффекта можно добиться корректировкой нескольких неверных бит на выходе первого слоя сети нейронов [17]. Увеличение количества решающих правил целесообразно проводить, пока правила ошибаются по-разному, т.е. не полностью коррелированы. Наилучший результат был получен сетью Байеса–Хемминга: FRR =0,0288; FAR=0,0232.

Работа частично выполнена (анализ недостатков глубоких искусственных нейронных сетей) при финансовой поддержке Министерства образования и науки РФ в рамках базовой части государственного задания в сфере научной деятельности (проект № 2.9314.2017/БЧ).

Экспериментальная часть работы выполнена при финансовой поддержке РФФИ (грант № 16-07-01204).