Оценка надежности вихревых систем термостатрования

Поволжское отделение Секции прикладных проблем РАН, г. Самара

В статье рассмотрена методика расчета вероятности безотказной работы и надежности вихревых источников холода для термостатирования.

При оценке надежности сложных систем, к которым относятся вихревые источники холода для поддержания стабильной температуры в бортовых отсеках летательных аппаратов, в частности вихревая система термостатирования, обычно необходимо определить вероятность исправной работы изделия P(t).

• 1.    Вероятность исправной работы изделия P(t) должна учитывать три вида отказов: катастрофический (внезапный), параметрический (постепенный) и перемежающийся. При расчетах надежности принимается допущение, что каждый вид отказа является не-зависимым событием.

• 2.    Следует различать при расчете:

В этом случае

P(t) = Pa(t)Pb(t)Pc(t), где Pa(t) – вероятность безотказной работы при катастрофических отказах; Pb(t) – вероятность безотказной работы при параметрических отказах; Pc(t) – вероятность безотказной работы при перемежающихся отказах.

Вероятность безотказной работы при перемежающихся отказах P_c(t) зависит от ряда факторов, плохо подчиняющихся учету. Поэтому обычно величину P_c(t) определяют экспериментально у готового изделия, а при предварительных расчетах считают P_c(t) = 1.

• а)    характер действия изделия – непрерывный или периодический;

• б)    возможность ремонта (восстановления) – неремонтируемые или ремонтируемые изделия;

• в)    неизменность структуры изделия в процессе работы – изделия с неизменной или изменяемой структурами.

• 3.    Изделие при расчете расчленяется на отдельные части, в отношении которых имеются или легко определяются самостоятельные количественные характеристики надежности. Обычно расчленение производится так, что отдельные части представляют собой конструктивно самостоятельные узлы, блоки или приборы и устройства, независимые в отношении отказов от других частей. Если отказы соседних частей (узлов, блоков и т. д.) зависят друг от друга, то их объединяют в одну общую часть, для которой находят расчетом (или экспериментальным путем) общую количественную характеристику надежности.

• 4.    Для расчета вероятности безотказной работы изделия составляют функциональную структурную схему изделия, в которую входят все элементы расчета надежности (т. е. узлы, блоки, приборы, устройства), необходимые для выполнения заданной основной функции изделия. Остальные элементы (узлы, блоки, приборы, устройства), несущие вспомогательные функции, например, функции контроля или сигнализации и т. п., обычно в схеме не показываются, а учет влияния их отказов на общую вероятность безотказной работы изделия производится при оценке вероятности безотказной работы тех элементов расчета надежности, с которыми они функционально связаны.

• 5.    Формулируются понятия отказа для всего изделия и для отдельных элементов расчета надежности как в отношении катастрофических, так и параметрических отказов.

• 6.    Составляется типовой график работы изделия либо на один цикл использования изделия (одна операция, одна смена, сутки, неделя, месяц, год), либо на весь срок службы изделия.

• 7.    Выбирается метод расчета надежности. Для различных этапов (разработки технического задания, эскизного, технического и рабочего проектов, этапа испытания созданной системы) разработки изделия выбирают различные по степени точности учета режимов и условий работы изделия и его элементов методы расчета.

• 8.    Степень достоверности расчета надежности зависит от принятых допущений:

Такие отдельные части, имеющие самостоятельные количественные характеристики надежности, называют элементом расчета надежности изделия.

Если необходимо, то в типовом графике учитываются фазы хранения и транспортировки до его использования.

Для каждого временного интервала (фазы) работы изделия и его элементов расчета надежности (узлов, блоков, приборов, устройств) указываются режимы (мощность, напряжение, скорость, усилие и т. д.) и условие работы (температура, влажность и т. п.).

• а)    при выборе зависимости изменения P(t);

• б)    при выборе величины интенсивности (опасности) отказов л, среднего времени между отказами Т_т и т. д.;

• в)    от полноты учета факторов, влияющих на надежность изделия; в частности учета: степени влияния отказов отдельных элементов на отказ изделия; наличия зависимости между отказами отдельных элементов; полноты учета влияния окружающей среды и других внешних влияний; степени приработки элементов перед их использованием; изменения надежности элементов во время хранения и транспортировки.

Далее необходимо определить и рассчитать нормы надежности. Обычно под нормой понимается величина показателя надежности, подлежащая обеспечению.

Норма надежности для изделия и его составных частей определяется при проработке требований по надежности, выданных в техническом задании, либо при эскизном проектировании изделия.

Норма надежности для ВСТ устанавли- вается в виде вероятности безотказной работы P(t) либо среднего времени безотказной работы Тт.

Определение норм надежности для изделия и элементов ВСТ производится обычно с помощью упрощенных расчетов, основанных на следующих допущениях:

вероятность безотказной работы при параметрических (и перемежающихся) отказах P_b(t ) = 1 и P_c(t) = 1;

закон изменения вероятности при катастрофических отказах экспоненциальный, т.е. опасность отказов не зависит от времени;

все элементы изделия равнонадежны.

Исходными данными при проведении расчетов являются:

• а)    количество элементов (агрегатов, узлов, приборов, устройств), входящих в изделие – N ;

• б)    требуемое время непрерывной исправной работы – t ₀. Если задана вероятность безотказной работы изделия (системы) Р , то

N

P ≤ ∏ P i , i = 1

где P_i – вероятность безотказной (исправной) работы любого элемента (блока, узла и т. п.). Считая все элементы (блоки, узлы и т.

п.) одинаковыми по надежности, имеем:

Pi ≥ N P или, при экспоненциальном законе:

P_i ≥ e N ⁰ = e ^-λ i ^t 0 ^, где λ – допустимая опасность отказа для изделия.

Следовательно, максимально допустимая опасность (интенсивность) отказа для элемента (узла, блока и т. д.) в среднем равна:

λ= ^λ i N

.

Полученное значение li имеет лишь приближенное (оценочное) значение, позволяющее оценить возможности построения бло- ков без дополнительных средств увеличения надежности его компонентов. Для этого берут некоторое значение lj для каждого из nj компонентов, входящих в блок, и определяют наличие неравенства:

nj

• х,. — Ух.

i                   j .

j = 1

В случае, если неравенство не выполняется, то следует рассмотреть различные способы увеличения надежности (облегчение режимов работы, замена комплектующих, резервирование).

Иногда задают время работы t ₀ и необходимое значение, вероятности безотказной работы P(t) с указанием для последней доверительного уровня у . При этом задании требуется, чтобы значение P(t) для t <  t ₀ было получено с вероятностью g. Обычно доверительный уровень g для систем, соответствующих по сложности САРТ, берут равным 0,8; 0,9 и реже 0,95; 0,99.

Если считать, что разброс значений P(t) подчиняется нормальному закону, то получим:

P (U — P^ - k о p , где s _p – среднеквадратичное отклонение разброса;

k – значение для различных доверительных уровней у подбирается по следующим данным:

у ...0,6   0,7 0,8   0,9 0,95 0,99

k 0,85 1,2   1,58 2,3 3,92 5,16

Если считать то

_1 - P (1q)y] + к о p или

Х + к о_х 1 0

[1- P (10)у] + к о p t0            t0

— Х + к о _х — X 1 + к

( о. )

[т]

.

С другой стороны, при

N

X —УХ,. — N X. ii i—1

и ох —

N

У 02. — NNои

XI             Xi i—1

и, следовательно,

0х — ^N0XL — 1 fOXLjX    NXi   NN ( Xi J

Значение коэффициента изменчивости

Oxl

XXi    x. зависит от технологии произ водств измерительных приборов. Обычно хх i — 0.08...0.2 в зависимости от вида компонента и качества его изготовления.

Допустимое значение опасности (интенсивности) отказов элементов

- in P ( 1 q ) _y t ₀

— X — X

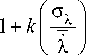
— N X i

1 +-M^X i NN (^X ,

или

^X i —-

N

1 +

X2

k

V N (

^O x i X

J

С целью более точного определения опасности отказов при организации мероприятий по повышению надежности ВСТ, достоверности измерительной информации и команд управления необходимо в процессе эксплуатации организовать сбор и статистическую обработку материалов по отказам комплектующих приборов и изделий.

Задачами такой обработки являются: определение вида функции плотности распределения отказов или вида функции (ин- тегральной) распределения отказов изделий; вычисление параметров полученного распределения; установление степени совпадения эмпирического распределения с предполагаемым теоретическим распределением;

определение параметров надежности исследуемых изделий.

Обычно в качестве типовых теоретических распределений рассматриваются экспоненциальное, гамма-распределение, нормальное или нормально-логарифмическое. В более сложных случаях приходится иметь дело с композициями двух и более типовых распределений, в этом случае данную композицию требуется представить в виде суммы составляющих (типовых) распределений и выполнить статистическое исследование каждого из них.

Для подбора вида теоретического распределения, достаточно близко подходящего к полученному эмпирическому распределению, чаще всего применяются методы максимума правдоподобия и метод наименьших квадратов.

В случае максимума правдоподобия стремятся найти такую функцию распределения, при которой максимизируется величина:

теристики только части распределения, а в отношении остальных изделий известно лишь то, что их наработка на отказ превышает длительность наблюдений или испытаний, то в этих случаях величина

r

i = 1

x i , x o , ^G x

X a

) + ⁽ n ^- r ) 1П ^{1 -} J ф ( x i , x o , ^G x ) dx

где n – число испытываемых изделий;

х_а – верхний предел выборки.

Величины х ₀ и у _х определяются по стандартным формулам.

Метод наименьших квадратов применяется для определения параметров распределения при полных выборках. Он заключается в подборе такой функции распределения заданного вида, при которой минимизируется величина

k s = £[ аэ ( xi)-am ( xi, X0,GX ) i=1

k

L = £ ln ф( i=1

x i , ^X 0, ^G x

),

где а э ( X i ) - экспериментальное значение параметра; а т ( X i , X q , G _x ) - теоретическое значение этого параметра при принятом виде распределения.

Для определения величин х ₀ и х_а состав-

где k – число групп (разрядов) измеряемой

– искомая функ-

ляются уравнения

и

^- = 0 ^dG x

.

ция плотности вероятности, подлежащая определению и зависящая от хo и ух; хо – мате-

матическое ожидание; G х - среднеквадратичное отклонение.

Для определения величин X q и G х со-

ставляются уравнения:

дL дxo

= 0

дL dG x

= 0

Если встречаются усеченные выборки, отличающиеся тем, что в процессе наблюдения или испытаний устанавливаются харак-

В качестве параметра изделия можно использовать либо х ₀ и σ ₀, либо, что обычно удобнее, параметры, характерные для данного вида распределения. Например х ₀ и X - в случае экспоненциального распределения; а , в и у - в случае распределения Вейбулла.

Для оценки степени совпадения эмпирической и теоретической кривых распределения применяются так называемые критерии согласия: критерий х ² (критерий Пирсона) или критерий Колмогорова.

Оценка по критерию х ² производится в следующем порядке:

1) разбивается область предполагаемого (гипотетического) распределения на l ин-

тервалов. Число l обычно берется равным 10– 20; при этом интервалы могут быть не равны друг другу;

• 2)    производится расчет величин np_i по формуле:

x i + 1

xi где хi, хi+1 – размеры i-гo интервала; p(x) – плотность гипотетического распределения;

• 3)    производится подсчет числа членов выборки v_i , попавших в каждый из l интервалов;

• 4)    определяется величина

  l

  x 2 = I

  i = 1

  
  

  ^{( v} j ^— nPj ) 2 np_i

  
  

• 5)    определяется число степеней свободы (число степеней свободы задачи или число степеней свободы случайных величин). При разбивке на l интервалов имеем всего l случайных величин v ₁, ..., v_l , связанных одной зависимостью:

  l

  
  

  I

  
  

  V i = n

  
  

i = 1

Отсюда следует, что число независимых случайных величин l – 1= k, т. е. имеется распределение cc2 с k = (l – 1) степенями свободы;

• 6)    по x 02 в таблице вероятностей P ( Х 2

> X q) находят значение P — вероятность того, что cc² может получить значение, равное или большее Х 2.

Если вероятность P ( Х > X q) мала, то предполагаемое (выбранное) теоретическое распределение неудовлетворительно представляет эмпирический материал.

Вместо таблиц вероятностей P ( Х

> Xq ) для оценки полученного значения Х можно пользоваться следующим:

• а)    коэффициентом точности

  H =

  
  

Х 2

.

l — 1

Если Н имеет значение от 0 до 2, то соответствие можно считать удовлетворительным;

• б)    критерием В. И. Романовского

  R =

  
  

  Х о ^— к

  
  
  
  
  

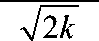
Если R < 3, то соответствие считается удовлетворительным.

В случае использования критерия А. Н. Колмогорова поступают следующим образом:

• 1)    для l интервалов, на которые разбивается эмпирическое распределение, составляются суммарные эмпирические распределения (накопленная частота), т. е. таблица:

• N ₁= nn₁; N ₂= N ₁+ nn₂; N ₃= N ₂+ nn₃;…; . N _l= n ;

• 2)    рассчитывается предполагаемая теоретическая интегральная функция распределения:

x

F (x )= J f (x)dt

—да и по ней – теоретическая накопленная численность:

N_iT • Ч = F(x) • Чп;

• 3)    находится разность между N_i и N_iT для каждого интервала и определяется верхняя граница (наибольшее значение) модуля разности между N_i и N_iT , т. е. D_max = || N_i – N_iT || и определяется число:

4)по таблицам находится значение Р ( Л ) - вероятности того, что модуль разности N_i – N_iT может быть больше или равен значению модуля, полученному из эмпирического материала.

Если Р(Л) мало, то теоретическое рас- пределение неудовлетворительно представляет эмпирический материал.

Часто оценку ведут прямо по значению Λ _а ; для удовлетворительного согласия эмпирического и теоретического распределения необходимо, чтобы Λ _а < [ Λ _max=1,5], при этом оптимальный интервал значений Λ _а ≤ 1,0.