Оценка напряженно-деформированного состояния сопряжения резьб треугольного и выпуклого профилей

В современной технике имеется большое количество задач, в которых требуется применение высокоточных линейных приводов. Одной из важнейших составляющих линейного привода является линейная передача, обеспечивающая преобразование вращательного движения вала двигателя в поступательное движение выходного звена. На сегодняшний день запатентовано много различных линейных передач, преобразование движения в которых осуществляется за счет резьбового сопряжения. Одной из актуальных задач при проектировании резьбы является обеспечение заданной нагрузочной способности и жесткости.

Предложен теоретический расчет напряженно-деформированного состояния резьбового сопряжения винта, имеющего выпуклый профиль резьбы, и гайки, имеющей треугольный профиль (рис. 1). Все расчеты проведены в системе СИ.

Основные параметры резьбы: шаг S ; количество витков N ; диаметр вершин профиля резьбы d ; угол профиля резьбы α ; радиус профиля резьбы винта R ;

S высота исходного профиля резьбы h ′ =       ; высота

2tg α

S рабочего профиля резьбы h=     -0,05S; угол

2tg α подъема резьбы y = arctg—; коэффициент трения f; п d

_ P , . f  P T - f

^Т конт                      ₇

F a - 1

осевое усилие P .

P sin a sin y- f

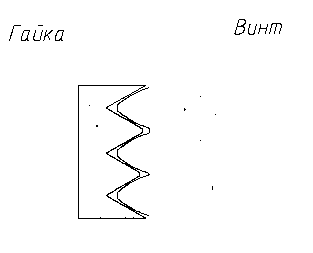
Рис. 1. Резьбовое сопряжение гайки с треугольным профилем резьбы и винта с выпуклым профилем резьбы

2, 262

PR cos a cos у \ NaJs ² +п² d²

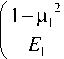
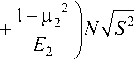
+ п² d ²

где F = a - 1 - площадь площадки контакта двух резьб.

Исходя из того, что гайка имеет в качестве образующей профиля резьбы линию, а винт – дугу радиусом R , примем в качестве модели их сопряжения модель контакта цилиндра и плоскости, результатом

взаимного сжатия которых является прямоугольная площадка, полуширина которой b определяется по формуле

b = 1,131

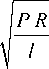
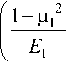
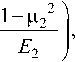
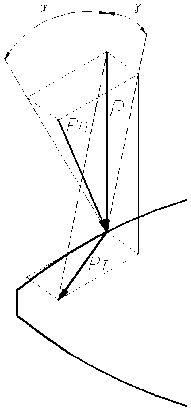
Рис. 2. Схема распределения осевого усилия на выпуклом профиле резьбы

где P – усилие поджатия цилиндра к плоскости; R – радиус цилиндра; l – длина линии контакта; p 1 , p 2 - коэффициенты Пуассона для материалов цилиндра и плоскости; E ₁, E ₂ – модули упругости для материалов цилиндра и плоскости [1].

Полная ширина прямоугольной площадки a , при сопряжении гайки с треугольным профилем резьбы и винта с выпуклым профилем радиусом R , определится по формуле

Определим изгибные напряжения в резьбе винта (рис. 3):

M а"зг = W ’

bh ²

где W =--момент сопротивления сечения.

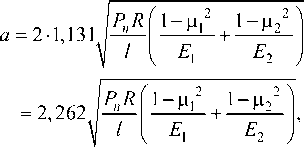
где l = N\ S ² + п ² d² - длина линии контакта.

Усилия в месте контакта (рис. 2) вычисляются по формулам

P_n = P cos α cos γ,

P τ = P sin α sin γ.

Получим зависимости для определения нормальных и касательных напряжений в месте контакта двух резьб:

Р Р nn

° конт             7

F a - l

_                  P cos a cos у

=                                                                  ,

₂,₂6₂ PR cos ^q cos у f 1-^ ₊ 1-p? ) ...^d

N ^Р 2 +ПР 1 E 1     E 2 J

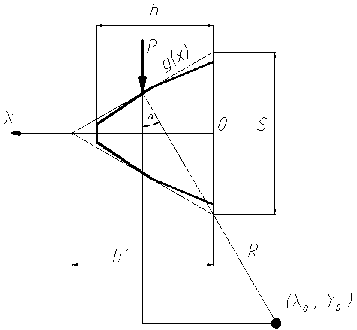
Рис. 3. Схема для расчета изгибных напряжений в выпуклой резьбе

Запишем выражение

3 P

Tmax = 2 f ’

где F – площадь поперечного сечения [1].

Так как момент сопротивления является функцией высоты профиля резьбы, определим закон ее изменения. Принимая за начало координат центр основания профиля резьбы, получим: ( x - x 0 ) 2 + ( y - y 0 ) 2 = R ² [2] – уравнение окружности, где x ₀ , y ₀ – координаты центра окружности; g ( x ) = 2(V R 2 - ( x - x 0 ) 2 + y 0 ) -уравнение профиля выпуклой резьбы винта;

W ( x ) = l ^- g 6 ^x ) .

Найдем центр окружности:

hS xn =--R sin a =--R sin a,

⁰ 2          4tg a

S y0 = — - R cos a,

( П       S'             S g (x) = 2 -I R2 - (x - (--R sin a ))2 +---R cos a

(v          4 tga              4

где х изменяется от 0 до _4t .

Таким образом, закон изменения момента сопротивления определится выражением

W ( x ) =

2 N - V s ² + n ² d²

(                  S                    S1

JR ² - ( x - (-- R sin a )) ² +--- R cos a

Ы        4tg a           4

X -—

Изгибные нормальные напряжения также превращается в функцию высоты профиля резьбы:

M (x) = P - x, где х изменяется от 0 до —---.

Запишем

= 3Px изг 2 N - V S ² + п² d ² x

(                                                                                                         1

SS x Ri - (x - (--R sin a)) +---R cos a

N 4tg a           4 J

Изгибные касательные напряжения также являются функцией высоты профиля резьбы:

3 P

^T max ⁽ x ) = ~ _;    / -. =

2 l - g ( x )

3 P

• ⁴ N - V S ² +n ² d ² x

  

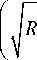
  - ( x - (— SR sin a )) ² + S - R cos a

  4tg a             4

  
  

Определим изгибные напряжения в треугольной резьбе гайки (рис. 4).

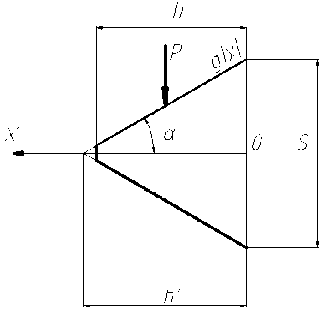
Рис. 4. Схема для расчета изгибных напряжений в треугольной резьбе

Определим уравнение профиля треугольной резьбы гайки. Принимая за начало координат центр основания профиля резьбы, получим уравнение профиля треугольной резьбы гайки:

g(x) = -2tga - x + S, а также

W ( x ) = l ^{- ( -} 2 x t^{g a} + S ⁾² =

= N - V s ² +n ² d ² - ( - 2 x tg a + S ) ²

=               6

где х изменяется от 0 до _4t .

Изгибные нормальные напряжения в треугольной резьбе определятся формулой

6 M ( x )

ст_изг ( x ) =----,            =-------------------=

NaIS ² +n ² d ² ( - 2 x tg a + S ) ²

= __________ 6 Px __________

N^S ² +n ² d ² ( - 2 x tg a + S ) ²

Анализируя данную зависимость, можно сделать вывод о том, что при равных параметрах резьбы и при одинаковых нагрузках треугольная резьба обладает большей несущей способностью, чем выпуклая, ввиду возникновения меньших нормальных напряжений.

Изгибные касательные напряжения в треугольной резьбе также являются функцией высоты профиля резьбы:

3 P

^T max ⁽ x ) = T , x 2 l - g ( x )

3 P

• ² N - V S ² +П ² d ² - ( - 2 x tg a + S )

Анализируя данную зависимость, можно сделать вывод о незначительном различии в величине касательных изгибных напряжениях между треугольной и выпуклой резьбами.

Используя полученные математические зависимости, можно на стадии проектирования винта и гайки рассчитать контактные и изгибные напряжения, возникающие в процессе нагружения в резьбе. Кроме того, варьируя шагом, диаметром, углом профиля, радиусом выпуклости резьбы, можно подобрать такую резьбу, которая бы отвечала заданным требованиям по жесткости и нагрузочной способности.