Оценка напряженно-деформированного состояния вращающегося длинного цилиндра

Тяжелый длинный полый цилиндр защемлен на конце и вращается вокруг продольной оси. Напряженно-деформированное состояние такого объекта в общем случае можно описать с применением современной высокопроизводительной вычислительной техники на основе трехмерной математической модели, включающей полную систему уравнений равновесия, определяющих соотношений упругопластического деформирования, учитывающих эффекты циклического нагружения материала, с соответствующими начальными и граничными условиями.

В первом приближении решение этой задачи может быть получено с использованием инженерных подходов на основе простейших соотношений теории упругости, сопротивления материалов и механики материалов [1-4].

1.    Изгиб длинного полого цилиндра под действием силы тяжести

Изгиб длинного полого цилиндра под действием силы тяжести (рис. 1) описывается дифференциальным уравнением четвертого порядка [1, 2]

d4 u (x)     , х

EI,     = q ( ^x )

d x ⁴

с граничными условиями u ( x ) x=0 = 0’

du (x)

dx

- 0,

x = 0

d2 u (x)     M (x)

d x ²

x = l

EI

x = I

= 0,

d3 u (x )      Q ( x )

dx3        EI x=l

В формулах (1)-(5) обозначено: u ( x ) - функция прогиба цилиндра; x - продольная координата; ^ - ось изогнутой балки; Mx ) - внешний изгибающий момент; Q ( x ) - внешняя перерезывающая сила; q ( x ) -распределенная массовая нагрузка, причем q ( x ) = m₀g = const, где m о -погонная масса цилиндра; g - ускорение свободного падения (9,81 м/с²).

Для вычислений принято, что длина цилиндра l = 10 м, его масса m = 1200 кг, внешний и внутренний диаметры d e = 0,176 ми d i = 0,128 м соответственно. Модуль упругости материала E = 2 - 10 ⁵ МПа.

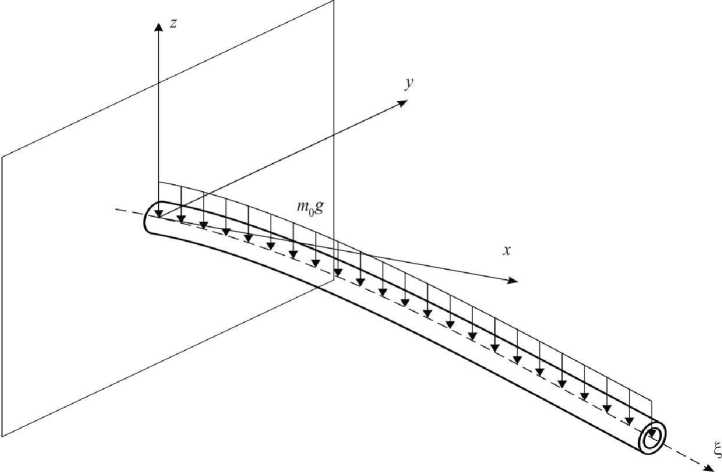
Рис. 1. Расчетная схема изгиба длинного полого цилиндра под действием силы тяжести

Решение дифференциального уравнения (1) записывается в виде [5, 6]

u ( x ) = C + Cx + Cx ² + Cx ³ + m ^{0 g} x ⁴,             (6)

V /   01    2    3   24EI причем постоянные C0, C1, C2, C3 определяются с учетом граничных условий (2)-(5):

u(x4  = C _n + C 0 + C 0² + C 0³ + mg- 0⁴ = 0,

V A x=0    0    1      2       3     24EI d и ( x) dx

x = 0

C + 2 Cx + 3C,x ² + mg x ³

1      2       3      _{6 EI}

- x = 0

= C + 2 C ₂ 0 + 3 C 0² + mg 0³ = 0, 1      2       3       _{6 EI}

d² и ( x ) d x ²

x = 1

= 2 C ₂ + 6 C₃x + m 0 g x 2

- 2       ^{3    2} EI J x = l

= 2 C ₂ + 3 C₃1 + mg 1 ² = 0,

2     3    _{2 EI}

d³ и ( x ) d x ³

= 6 C 3 +

x = 1

mg x

^EI J x = 1

= 6 C ₃ + mg 1 = 0.

3 _EI

Решение системы линейных алгебраических уравнений (7) зволяет определить постоянные интегрирования:

no-

C _o = 0, C = 0, C ₂ = mg , C ₃ =- mg

.

^{0       1       2}    4 EI ³     6 EI

Решение (6) принимает вид и (x) =

m ₀ g 4 m ₀ gl 3   m ₀ gl ² 2    m ₀ g 2

----x--x +-- x —----x

24 EI

6 EI

4 EI

24 EI

( x ² - 4 lx + 6 1 ² ) .

Кривизна осевой линии цилиндра определяется выражением d2u(xj m0 g .

K =----— =---x dx2    2EI

m о gl x ₊ m o gl l

EI

2 EI

= m ^ g (x 2 — 2 lx + 1 2).

2 EI

На рис. 2, а приведена форма, на рис. 2, б - кривизна прогиба центральной линии длинномерного цилиндра. Наибольшая кривизна, м^-1, (см. рис. 2, б ) имеет место в точке x = 0,

^Kl x = 0

= mg ₀ 2 _— ^m 0 gl _{0 +} m 0 gl ² = ^m 0 gll

2 EI

EI

2 EI    2 EI

- 0,008229,

а значит, наибольшие растягивающие (сжимающие) напряжения, МПа, в длинномерном цилиндре достигаются именно в этом сечении,

d отя x = — Eктах — = 144,84.

max       max ₂

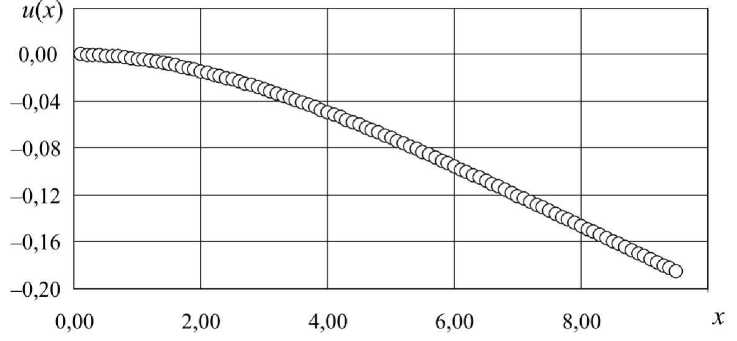
а

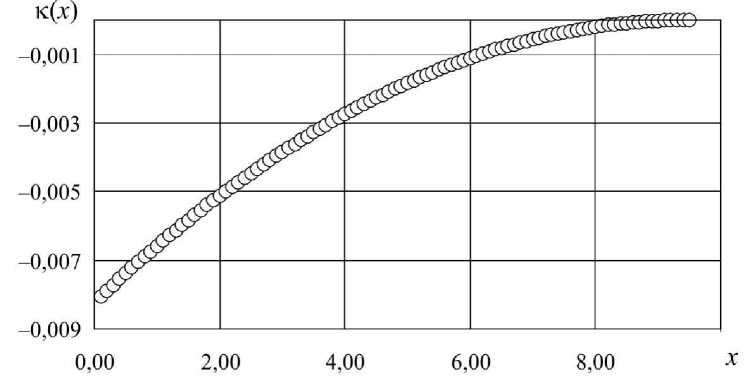
б

Рис. 2. Действие силы тяжести на ось длинномерного цилиндра: а - зависимость от продольной координаты х (м) прогиба и (м); б - зависимость от продольной координаты х (м) и кривизны к (м^-1)

2.    Изгиб вращающегося длинного цилиндра

Изгиб вращающегося длинного цилиндра обусловлен одновременным действием силы тяжести и вращения за счет момента M _кр внешних сил (рис. 3).

Наложение дополнительных факторов (продольное перемещение, вращение и проч.) при изгибе длинномерных изделий приводит к формированию сложного напряженного и деформированного состояния [7-10]. Моделирование таких процессов требует применения эйлероволагранжева подхода, прослеживания истории деформирования материальных частиц, в том числе процессов нагружения, упругой разгрузки и, возможно, упругопластического нагружения противоположного зна- ка, в том числе с появлением вторичных пластических деформаций и изменением предела текучести материала (эффект Баушингера), учета прочих особенностей знакопеременного деформирования.

Очевидно, что при упругом изгибе наложение вращения не приводит к изменению упругой линии длинномерного изделия, поскольку для его вращения практически не требуются дополнительные энергетические затраты (кроме возможных затрат на трение): при повороте круглого сечения энергия, затрачиваемая на нагружение частиц материала, равна упругой энергии разгрузки симметрично расположенных частиц того же сечения.

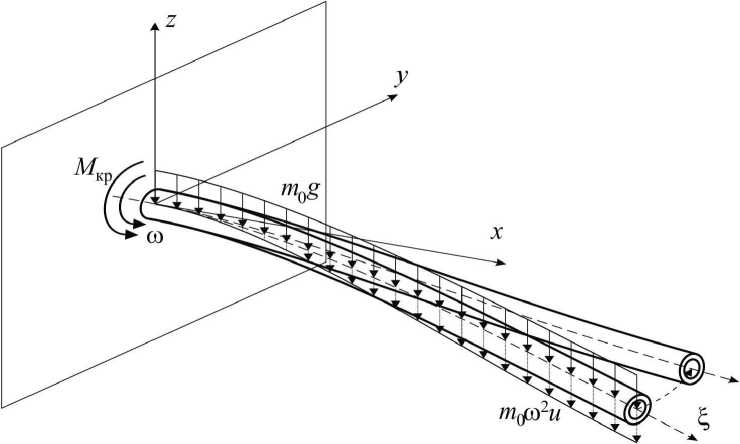
Рис. 3. Расчетная схема изгиба и вращения длинного полого цилиндра

При наличии зоны пластических деформаций в области высоких значений кривизны продольной оси цилиндра (например, область защемления левого конца длинного цилиндра на рис. 2) ситуация меняется существенно, поскольку в результате пластического нагружения формируется остаточная кривизна цилиндра. Вращение цилиндра вокруг продольной оси £ (см. рис. 3) требует значительных затрат на преодоление остаточной кривизны, и энергетически более выгодным становится вращение цилиндра с искривленной осью вокруг оси x .

Оценка напряженно-деформированного состояния длинного цилиндра, изогнутого под действием собственного веса и поворачивающегося вокруг оси x, может быть выполнена приближенно с привлечением уравнений механики материалов. Для учета динамической нагрузки, возникающей при вращении объекта, может быть применен принцип Даламбера [11], согласно которому ко всем действующим внешним силам необходимо добавить силы инерции, равные в рассматриваемом случае m0® и, где to и - центростремительное ускорение; ю - угловая скорость вращения длинномерного цилиндра под действием момента Mкр; и - прогиб оси цилиндра, равный расстоянию от оси вращения x.

В рассматриваемом случае наибольший прогиб, а значит, и наиболее опасное напряженно-деформированное состояние длинного цилиндра имеют место в низшем положении объекта, когда массовые силы тяжести суммируются с силами инерции (см. рис. 3). При прочих положениях цилиндра эти силы частично или полностью компенсируют друг друга. Уравнение изгиба центральной линии длинномерного цилиндра, учитывающее действие сил инерции, имеет вид [1, 2, 4]

EI

d⁴ и ( x ) d x ⁴

= m₀ g + m ₀to² и ( x )

с теми же граничными условиями (2)-(5). Решение неоднородного дифференциального уравнения (10) четвертого порядка представляется суммой [5, 6] общего решения и 1 ( x ) однородного дифференциального уравнения

EI

d⁴ и 1 ( x ) d x ⁴

m ₀to² и 1 ( x ) = 0

и частного решения и ₂ ( x ) неоднородного уравнения

d4и2 (x)        2 . .

EI — d^4 ^_ m ₀to и 2 ( x ) = m ₀ g •

Общее решение и 1 ( x ) уравнения (11) строится в виде [5, 6]

и 1 ( x ) = Ae °x ,

частное решение и ₂ ( x ) уравнения (12) согласно [5, 6] разыскивается в виде

и ₂ ( x ) = B ,

соответствующем виду правой части уравнения (12), где A , B и а - искомые константы. Подстановка решения (13) в однородное дифференциальное уравнение (11) приводит к характеристическому уравнению

EI a ⁴ Ae ^a - m ₀ю ² Ae ^a = 0.

Введение обозначения D4 = m0®2 /EI дает возможность представить полученное соотношение в виде алгебраического уравнения четвертой степени a4 = D 4, корни которого

• a , = + D , a₂ = - D , a₃₁ = iD , a₄ = - iD ,

где i = V-1 - мнимая (комплексная) единица. Общее решение однородного дифференциального уравнения (11) принимает вид u1 (x) = A1 eDx + A2 e- Dx + A3 eiDx + A4 e- iDx.

Подстановка решения (14) в неоднородное дифференциальное уравнение (12) приводит к уравнению относительно константы B :

• - т ₀ш ² B = m ₀ g ,

откуда следует, что B = -g/го2 . В итоге решение дифференциального уравнения (10) записывается в виде u (x) = u1 (x) + u2 (x) = A1 eDx + A2 e-Dx + A3 eiDx + A4 e-iDx - -g-го2

или, с учетом формулы Эйлера [5], u (x ) = A1 eDx + A2 e"Dx + A3cos Dx + A 4sin Dx - -g-.        (15)

го2

Для нахождения значения постоянных интегрирования A 1 , A ₂, A ₃, A ₄ используются граничные условия (2)-(5)

u ⁽ x Л x = 0

A.e Dx + A,e Dx + A₃ cos Dx + A₄ sin Dx - -Д = 0, ^{1         2          3             4}           O² J x = 0

d u ( x ) d x

d² u ( x )

d x ²

x = 0

x = l

d³ u ( x )

d x ³

x = l

A 1 De^Dx - A 2 De ^Dx - A 3 D sin Dx + A ₄ D cos Dx

= 0, x = 0

A 1 D ² e^Dx + A ₂ D ² e ^{- Dx} - A 3 D ² cos Dx - A 4 D ² sin Dx J = l = 0, (16)

A 1 D ³ e^Dx - A ₂ D ³ e ^Dx + A 3 D ³ sin Dx - A 4 D ³ cos Dx l = 0.

Соотношения (16) представляют собой систему четырех линейных алгебраических уравнений относительно искомых величин

A 1, A 2 , A 3	, A 4 :
	1 A 1      + 1 A 2        + 1 A 3         + 0 A 4          = ^2
1	DA 1 - DA 2 + 0 A 3 + DA 4 = 0, D 2 eDA 1 + D 2 e - DlA 2 - D 2cos DlA3 - D 2 sin DlA 4 = 0, _ eDlD 3 A 1 - e - Dl D 3 A 2 + D 3 sin DlA3 - D 3 cos DlA 4 = 0.

Решение полученной системы линейных алгебраических уравнений для принятых ранее данных и угловой скорости вращения to = 2л/3 с^-1 позволяет определить постоянные интегрирования

A 1 =- 0,27618, A ₂ =- 1,3187, A 3 =- 0,64157, A 4 =- 1,0425.

Решение (15) принимает вид

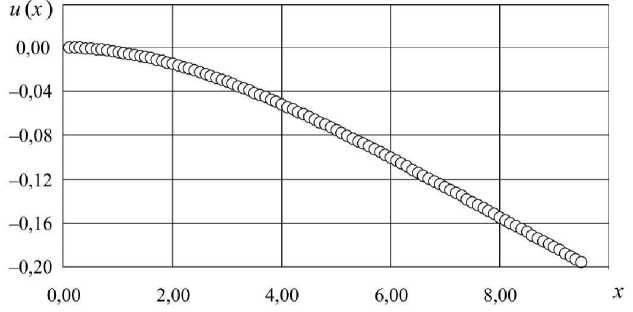
u ( x ) = - 0,27618 e^Dx - 1,3187 e " ^Dx - 0,64157cos Dx - 1,0425sin Dx - Дт , (17) o ²

где D = 0,095218, м^-1.

На рис. 4 приведены форма прогиба осевой линии длинномерного цилиндра и ее кривизна, которая определяется выражением к = d-u^ = -d2 (0,27618eDx +1,3187e"Dx -            m dx2                                               (18)

- 0,64157cosD x - 1,0425sinD x ) .

Наибольшая кривизна (см. рис. 4, б) имеет место в точке x = 0, к   = -D2(0,27618-D0 +1,3187e-D0 - x=0

• - 0,64157cos0 - 1,0425sin0 ) = - 0,00864 м^-1,

а значит, наибольшие (по модулю) растягивающие и сжимающие напряжения в длинномерном изделии достигаются именно в этом сечении, d о   =- Eк   - = 152,11 МПа.

max       max ₂

По сравнению с результатами, полученными при расчете напряжения при изгибе под действием силы тяжести, инерция вращательного движения повысила максимальное напряжение на 7,27 МПа, или на 5 %.

а

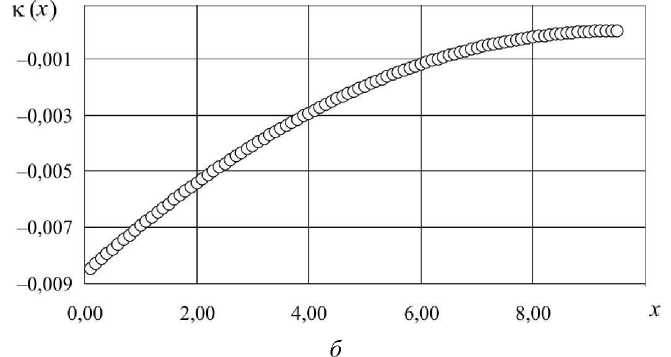
Рис. 4. Действие силы тяжести и вращения на ось длинномерного цилиндра: а - зависимость от продольной координаты x (м) прогиба и (м); б - зависимость от продольной координаты x (м) кривизны к (м ' )

3. Сдвиговые напряжения от крутящего момента

Определение величины касательного напряжения от действия крутящего момента М _кр, приложенного к длинномерному цилиндру, выполняется согласно [1, 2, 4]:

т =

М кр I p

r

где r - расстояние от оси кручения до рассматриваемой точки; I p - полярный момент инерции поперечного сечения. Для заданных диаметрах d e и d i цилиндра и величине крутящего момента М _кр = 11250 кН - м максимальное сдвиговое напряжение определяется величиной

M ттах= — — = 14,59 МПа. max

Ip 1

Учитывая сложное напряженное состояние длинномерного цилиндра, испытывающего растягивающее напряжение от изгибающих нагрузок и сдвиговое напряжение от крутящего момента, эквивалентное (суммарное) напряжение следует определять с использованием понятия интенсивности напряжения о i , определяемого общим выражением [1, 4, 12]

о = + \W° x - °v ) 2 + ( °v “ о ) 2 ⁺( °z “ °_х ) ^{2 + 6} ( T 2V + т^ + т^ ) . (20) x y         y z z x          xy yz zx

В рассматриваемом случае, учитывая o_max = 152,11 МПа и т_тах = 14,59 МПа, эквивалентное напряжение принимает значение

О = 70L+35Z = 154,19 МПа. I у max max        ^v

Выводы

Основным фактором, определяющим напряженно-деформированное состояние длинного цилиндра, является изгиб за счет собственного веса. Вращение длинного цилиндра вокруг собственной оси обеспечивает знакопеременное нагружение периферийных слоев длинного цилиндра. Дополнительное вращение длинного цилиндра, обусловленное наличием инерционных массовых сил, способствовало увеличению амплитудного значения напряжения на 5 %. Наличие крутящего момента привело к появлению сдвиговых напряжений, достигающих максимального значения на поверхности длинного цилиндра. Эквивалентное напряжение, учитывающее сложное напряженное состояние, увеличилось по сравнению с изгибом и вращением на 1,4 %.