Оценка недвижимости для налогообложения
Автор: Грибовский С.В., Баринов Н.П.
Журнал: Имущественные отношения в Российской Федерации @iovrf
Рубрика: Блокнот практика
Статья в выпуске: 6 (57), 2006 года.
Бесплатный доступ
Короткий адрес: https://sciup.org/170151480
IDR: 170151480
Текст статьи Оценка недвижимости для налогообложения
С.В. Грибовский заместитель начальника ГУ «Городское управление инвентаризации и оценки недвижимости» (Санкт-Петербург), профессор, доктор экономических наук Н.П. Баринов генеральный директор ООО «Оценочная фирма «БОСИ» (Санкт-Петербург), старший научный сотрудник, кандидат технических наук
-
2. Выбор модели оценки стоимости
Для оценки недвижимости для целей налогообложения на активных рынках рекомендуется использовать мультипликативную модель следующего вида:
СТОИМОСТЬ ОБЪЕКТА = С Б х К 1 х ... х Кп х ПЛОЩАДЬ. (1)
В дальнейшем для упрощения изложения параметр «площадь» временно опустим, то есть под ценой будем понимать удельную стоимость единицы площади, а вместо переменной «стоимость объекта» будем использовать ее математический аналог – переменную.
В рамках сформулированной постановки задачи рассмотрим алгоритмы построения трех мультипликативных моделей оценки стоимости:
-
• модели, основанной на методе регрессионного анализа;
-
• кластерной модели, основанной на методе параллельных сечений;
-
• кластерной модели, основанной на методе последовательных сечений;
-
2.1. Модель, основанная на методе регрессионного анализа
Практика оценки недвижимости показывает, что в классе моделей (1) достаточно хорошими аппроксимирующими свойствами обладает регрессионная мультипликативная2 модель следующего вида:
у = а 0 х a l 1 х a 2 2 х...х а ^ . (2)
Параметры a 0, a 1,…, am этой модели определяются методом наименьших квадратов. Основная задача модели оценки стоимости – моделирование зависимости цены от ценообразующих факторов х 1, х 2, …, хm .
Для построения модели (2) одно из значений каждого ценообразующего фактора, которые представлены в таблице 2, выберем в качестве базового, и исключим из таблицы. Иначе говоря, для этих значений не будем выделять отдельные переменные. При этом объект недвижимости, имеющий базовые значения ценообразующих факторов, определим как эталонный объект. В качестве эталонного объекта недвижимости может быть выбран объект, обладающий любыми характеристиками, например наиболее типичный или наиболее распространенный объект недвижимости. Выберем в оцениваемом поселении в качестве эталонного объекта 1-комнатную квартиру в кирпичном доме, находящуюся в 1-й зоне. С учетом этого составим таблицу обозначений и значений ценообразующих факторов (табл. 4).
Таблица 4
Описание ценообразующих факторов
|
Наименование ценообразующего фактора |
Обозначение ценообразующего фактора |
Значение ценообразующего фактора |
|
Зона 1 |
отсутствует |
Базовое |
|
Зона 2 |
x1 |
Наличие: x1 = 1, отсутствие: x1 = 0 |
|
Кирпичный дом |
отсутствует |
Базовое |
|
Блочный дом |
x 2 |
Наличие: x2 = 1, отсутствие: x2 = 0 |
|
Деревянный дом |
x 3 |
Наличие: x3 = 1, отсутствие: x3 = 0 |
|
1-комнатная квартира |
отсутствует |
Базовое |
|
2-комнатная квартира |
x4 |
Наличие: x4 = 1, отсутствие: x4 = 0 |
|
3-комнатная квартира |
x5 |
Наличие: x5 = 1, отсутствие: x5 = 0 |
|
4-комнатная квартира |
x 6 |
Наличие: x6 = 1, отсутствие: x6 = 0 |
|
Реальная цена |
y |
Реальное |
|
Оцениваемая стоимость |
Вычисляемое |
В соответствии с таблицей 4 на базе таблицы 3 составим усеченную (без базовых значений ценообразующих факторов) таблицу наблюдений (табл. 5). В этой таблице присутствуют значения всех факторов, за исключением базовых, характерных для эталонного объекта.
С учетом данных, представленных в таблице 5, модель оценки стоимости будет иметь следующий вид:
y = a 0 x a X 1 x a 2 2 x a X 3 x a 4 4 x a 5 5 x a 6 6 , (3)
где y ˆ – оценка рыночной стоимости одного квадратного метра квартиры;
а 0 – свободный параметр модели, представляющий собой стоимость одного квадратного метра общей площади эталонной квартиры (однокомнатной квартиры, находящейся в кирпичном доме в 1-й ценовой зоне);
а 1, а 2, …, а 6 – параметры модели, позволяющие скорректировать стоимость квартиры на местоположение, материал стен и количество комнат.
Если значения всех ценообразующих факторов в модели (3) будут равны нулю ( х1 = х2 = … = хm = 0), то оценка рыночной стоимости будет соответствовать стоимости эталонного объекта: y = a 0, то есть однокомнатной квартиры с кирпичными стенами, расположенной в 1-й ценовой зоне.
-
2.1.1. Расчет параметров модели оценки стоимости
Для расчета параметров модели (3) преобразуем ее в аддитивный вид путем логарифмирования:
Ln ( y ) = Ln ( a 0) + x 1 x Ln ( a 1 ) + x 2 x Ln ( a 2) +... + x 6 x Ln ( a 6 ). (4)
Для того чтобы с использованием компьютера рассчитать коэффициенты модели (4), необходимо предварительно заполнить таблицу значений наблюдений в обозначениях этой модели (табл. 6). Таблица 6 отличается от таблицы 5 тем, что в ней в соответствии с моделью (4) вместо цен используются их логарифмы.
Таблица 5
|
& s S |
cm <8 I О CO |
Дом |
Квартира |
RS з |
& s S |
cm <8 О CO |
Дом |
Квартира |
RS з |
||||||
|
2 'S о |
‘S |
RS cm |
co |
1 2 4 |
2 'S о |
'S i 2 & 4 |
CQ RS -> cm |
i 2 co |
i 2 4 |
||||||
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
800 |
55 |
0 |
0 |
1 |
0 |
0 |
1 |
840 |
|
2 |
0 |
0 |
0 |
0 |
0 |
0 |
802 |
56 |
0 |
0 |
1 |
0 |
0 |
1 |
860 |
|
3 |
0 |
0 |
0 |
0 |
0 |
0 |
750 |
57 |
1 |
0 |
0 |
0 |
0 |
0 |
960 |
|
4 |
0 |
0 |
0 |
0 |
0 |
0 |
760 |
58 |
1 |
0 |
0 |
0 |
0 |
0 |
962 |
|
5 |
0 |
0 |
0 |
0 |
0 |
0 |
798 |
59 |
1 |
0 |
0 |
0 |
0 |
0 |
912 |
|
6 |
0 |
0 |
0 |
0 |
0 |
0 |
804 |
60 |
1 |
0 |
0 |
0 |
0 |
0 |
958 |
|
7 |
0 |
0 |
0 |
1 |
0 |
0 |
880 |
61 |
1 |
0 |
0 |
0 |
0 |
0 |
966 |
|
8 |
0 |
0 |
0 |
1 |
0 |
0 |
805 |
62 |
1 |
0 |
0 |
1 |
0 |
0 |
850 |
|
9 |
0 |
0 |
0 |
1 |
0 |
0 |
860 |
63 |
1 |
0 |
0 |
1 |
0 |
0 |
1033 |
|
10 |
0 |
0 |
0 |
1 |
0 |
0 |
880 |
64 |
1 |
0 |
0 |
1 |
0 |
0 |
1050 |
|
11 |
0 |
0 |
0 |
0 |
1 |
0 |
965 |
65 |
1 |
0 |
0 |
0 |
1 |
0 |
1158 |
|
12 |
0 |
0 |
0 |
0 |
1 |
0 |
989 |
66 |
1 |
0 |
0 |
0 |
1 |
0 |
1166 |
|
13 |
0 |
0 |
0 |
0 |
1 |
0 |
910 |
67 |
1 |
0 |
0 |
0 |
1 |
0 |
1188 |
|
14 |
0 |
0 |
0 |
0 |
1 |
0 |
990 |
68 |
1 |
0 |
0 |
0 |
1 |
0 |
1122 |
|
15 |
0 |
0 |
0 |
0 |
1 |
0 |
960 |
69 |
1 |
0 |
0 |
0 |
1 |
0 |
1133 |
|
16 |
0 |
0 |
0 |
0 |
1 |
0 |
969 |
70 |
1 |
0 |
0 |
0 |
0 |
1 |
1280 |
|
17 |
0 |
0 |
0 |
0 |
0 |
1 |
1050 |
71 |
1 |
0 |
0 |
0 |
0 |
1 |
1270 |
|
18 |
0 |
0 |
0 |
0 |
0 |
1 |
1068 |
72 |
1 |
0 |
0 |
0 |
0 |
1 |
1260 |
|
19 |
0 |
0 |
0 |
0 |
0 |
1 |
1058 |
73 |
1 |
0 |
0 |
0 |
0 |
1 |
1200 |
|
20 |
0 |
0 |
0 |
0 |
0 |
1 |
1050 |
74 |
1 |
0 |
0 |
0 |
0 |
1 |
1260 |
|
21 |
0 |
1 |
0 |
0 |
0 |
0 |
713 |
75 |
1 |
1 |
0 |
0 |
0 |
0 |
870 |
|
22 |
0 |
1 |
0 |
0 |
0 |
0 |
715 |
76 |
1 |
1 |
0 |
0 |
0 |
0 |
840 |
|
23 |
0 |
1 |
0 |
0 |
0 |
0 |
727 |
77 |
1 |
1 |
0 |
0 |
0 |
0 |
850 |
|
24 |
0 |
1 |
0 |
0 |
0 |
0 |
740 |
78 |
1 |
1 |
0 |
0 |
0 |
0 |
880 |
|
25 |
0 |
1 |
0 |
1 |
0 |
0 |
780 |
79 |
1 |
1 |
0 |
1 |
0 |
0 |
970 |
|
26 |
0 |
1 |
0 |
1 |
0 |
0 |
810 |
80 |
1 |
1 |
0 |
1 |
0 |
0 |
960 |
|
27 |
0 |
1 |
0 |
1 |
0 |
0 |
788 |
81 |
1 |
1 |
0 |
1 |
0 |
0 |
930 |
|
28 |
0 |
1 |
0 |
0 |
1 |
0 |
880 |
82 |
1 |
1 |
0 |
1 |
0 |
0 |
955 |
|
29 |
0 |
1 |
0 |
0 |
1 |
0 |
870 |
83 |
1 |
1 |
0 |
0 |
1 |
0 |
1020 |
|
30 |
0 |
1 |
0 |
0 |
1 |
0 |
850 |
84 |
1 |
1 |
0 |
0 |
1 |
0 |
1044 |
|
31 |
0 |
1 |
0 |
0 |
1 |
0 |
900 |
85 |
1 |
1 |
0 |
0 |
1 |
0 |
1025 |
|
32 |
0 |
1 |
0 |
0 |
1 |
0 |
860 |
86 |
1 |
1 |
0 |
0 |
1 |
0 |
1045 |
|
33 |
0 |
1 |
0 |
0 |
0 |
1 |
905 |
87 |
1 |
1 |
0 |
0 |
1 |
0 |
1000 |
|
34 |
0 |
1 |
0 |
0 |
0 |
1 |
945 |
88 |
1 |
1 |
0 |
0 |
0 |
1 |
1144 |
|
35 |
0 |
1 |
0 |
0 |
0 |
1 |
1000 |
89 |
1 |
1 |
0 |
0 |
0 |
1 |
1177 |
|
36 |
0 |
1 |
0 |
0 |
0 |
1 |
920 |
90 |
1 |
1 |
0 |
0 |
0 |
1 |
1188 |
|
37 |
0 |
1 |
0 |
0 |
0 |
1 |
940 |
91 |
1 |
1 |
0 |
0 |
0 |
1 |
1057 |
|
38 |
0 |
0 |
1 |
0 |
0 |
0 |
635 |
92 |
1 |
1 |
0 |
0 |
0 |
1 |
1111 |
|
39 |
0 |
0 |
1 |
0 |
0 |
0 |
600 |
93 |
1 |
0 |
1 |
0 |
0 |
0 |
777 |
|
40 |
0 |
0 |
1 |
0 |
0 |
0 |
640 |
94 |
1 |
0 |
1 |
0 |
0 |
0 |
780 |
|
41 |
0 |
0 |
1 |
0 |
0 |
0 |
620 |
95 |
1 |
0 |
1 |
0 |
0 |
0 |
1000 |
|
42 |
0 |
0 |
1 |
0 |
0 |
0 |
650 |
96 |
1 |
0 |
1 |
1 |
0 |
0 |
850 |
|
43 |
0 |
0 |
1 |
0 |
0 |
0 |
642 |
97 |
1 |
0 |
1 |
1 |
0 |
0 |
860 |
|
44 |
0 |
0 |
1 |
1 |
0 |
0 |
900 |
98 |
1 |
0 |
1 |
1 |
0 |
0 |
866 |
|
45 |
0 |
0 |
1 |
1 |
0 |
0 |
740 |
99 |
1 |
0 |
1 |
1 |
0 |
0 |
840 |
|
46 |
0 |
0 |
1 |
1 |
0 |
0 |
700 |
100 |
1 |
0 |
1 |
1 |
0 |
0 |
830 |
|
47 |
0 |
0 |
1 |
0 |
1 |
0 |
789 |
101 |
1 |
0 |
1 |
0 |
1 |
0 |
900 |
|
48 |
0 |
0 |
1 |
0 |
1 |
0 |
780 |
102 |
1 |
0 |
1 |
0 |
1 |
0 |
1160 |
|
49 |
0 |
0 |
1 |
0 |
1 |
0 |
760 |
103 |
1 |
0 |
1 |
0 |
1 |
0 |
930 |
|
50 |
0 |
0 |
1 |
0 |
1 |
0 |
830 |
104 |
1 |
0 |
1 |
0 |
1 |
0 |
940 |
|
51 |
0 |
0 |
1 |
0 |
1 |
0 |
750 |
105 |
1 |
0 |
1 |
0 |
0 |
1 |
1050 |
|
52 |
0 |
0 |
1 |
0 |
0 |
1 |
810 |
106 |
1 |
0 |
1 |
0 |
0 |
1 |
800 |
|
53 |
0 |
0 |
1 |
0 |
0 |
1 |
840 |
107 |
1 |
0 |
1 |
0 |
0 |
1 |
900 |
|
54 |
0 |
0 |
1 |
0 |
0 |
1 |
870 |
108 |
1 |
0 |
1 |
0 |
0 |
1 |
1000 |
Таблица 6
|
& s S |
cm <0 |
Дом |
Квартира |
c c |
& S |
cm <8 |
Дом |
Квартира |
c c |
||||||
|
2 'X о |
s Cb & |
Os RS s -> i ^ |
1 2 ? co |
1 5 ? st |
2 'X о |
‘S S ^ & 4 |
OS s -> ? cm |
i 2 co |
i 5 St |
||||||
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
6,685 |
55 |
0 |
0 |
1 |
0 |
0 |
1 |
6,733 |
|
2 |
0 |
0 |
0 |
0 |
0 |
0 |
6,687 |
56 |
0 |
0 |
1 |
0 |
0 |
1 |
6,757 |
|
3 |
0 |
0 |
0 |
0 |
0 |
0 |
6,620 |
57 |
1 |
0 |
0 |
0 |
0 |
0 |
6,867 |
|
4 |
0 |
0 |
0 |
0 |
0 |
0 |
6,633 |
58 |
1 |
0 |
0 |
0 |
0 |
0 |
6,869 |
|
5 |
0 |
0 |
0 |
0 |
0 |
0 |
6,682 |
59 |
1 |
0 |
0 |
0 |
0 |
0 |
6,816 |
|
6 |
0 |
0 |
0 |
0 |
0 |
0 |
6,690 |
60 |
1 |
0 |
0 |
0 |
0 |
0 |
6,865 |
|
7 |
0 |
0 |
0 |
1 |
0 |
0 |
6,780 |
61 |
1 |
0 |
0 |
0 |
0 |
0 |
6,873 |
|
8 |
0 |
0 |
0 |
1 |
0 |
0 |
6,691 |
62 |
1 |
0 |
0 |
1 |
0 |
0 |
6,745 |
|
9 |
0 |
0 |
0 |
1 |
0 |
0 |
6,757 |
63 |
1 |
0 |
0 |
1 |
0 |
0 |
6,940 |
|
10 |
0 |
0 |
0 |
1 |
0 |
0 |
6,780 |
64 |
1 |
0 |
0 |
1 |
0 |
0 |
6,957 |
|
11 |
0 |
0 |
0 |
0 |
1 |
0 |
6,872 |
65 |
1 |
0 |
0 |
0 |
1 |
0 |
7,054 |
|
12 |
0 |
0 |
0 |
0 |
1 |
0 |
6,897 |
66 |
1 |
0 |
0 |
0 |
1 |
0 |
7,061 |
|
13 |
0 |
0 |
0 |
0 |
1 |
0 |
6,813 |
67 |
1 |
0 |
0 |
0 |
1 |
0 |
7,080 |
|
14 |
0 |
0 |
0 |
0 |
1 |
0 |
6,898 |
68 |
1 |
0 |
0 |
0 |
1 |
0 |
7,023 |
|
15 |
0 |
0 |
0 |
0 |
1 |
0 |
6,867 |
69 |
1 |
0 |
0 |
0 |
1 |
0 |
7,033 |
|
16 |
0 |
0 |
0 |
0 |
1 |
0 |
6,876 |
70 |
1 |
0 |
0 |
0 |
0 |
1 |
7,155 |
|
17 |
0 |
0 |
0 |
0 |
0 |
1 |
6,957 |
71 |
1 |
0 |
0 |
0 |
0 |
1 |
7,147 |
|
18 |
0 |
0 |
0 |
0 |
0 |
1 |
6,974 |
72 |
1 |
0 |
0 |
0 |
0 |
1 |
7,139 |
|
19 |
0 |
0 |
0 |
0 |
0 |
1 |
6,964 |
73 |
1 |
0 |
0 |
0 |
0 |
1 |
7,090 |
|
20 |
0 |
0 |
0 |
0 |
0 |
1 |
6,957 |
74 |
1 |
0 |
0 |
0 |
0 |
1 |
7,139 |
|
21 |
0 |
1 |
0 |
0 |
0 |
0 |
6,569 |
75 |
1 |
1 |
0 |
0 |
0 |
0 |
6,768 |
|
22 |
0 |
1 |
0 |
0 |
0 |
0 |
6,572 |
76 |
1 |
1 |
0 |
0 |
0 |
0 |
6,733 |
|
23 |
0 |
1 |
0 |
0 |
0 |
0 |
6,589 |
77 |
1 |
1 |
0 |
0 |
0 |
0 |
6,745 |
|
24 |
0 |
1 |
0 |
0 |
0 |
0 |
6,607 |
78 |
1 |
1 |
0 |
0 |
0 |
0 |
6,780 |
|
25 |
0 |
1 |
0 |
1 |
0 |
0 |
6,659 |
79 |
1 |
1 |
0 |
1 |
0 |
0 |
6,877 |
|
26 |
0 |
1 |
0 |
1 |
0 |
0 |
6,697 |
80 |
1 |
1 |
0 |
1 |
0 |
0 |
6,867 |
|
27 |
0 |
1 |
0 |
1 |
0 |
0 |
6,669 |
81 |
1 |
1 |
0 |
1 |
0 |
0 |
6,835 |
|
28 |
0 |
1 |
0 |
0 |
1 |
0 |
6,780 |
82 |
1 |
1 |
0 |
1 |
0 |
0 |
6,862 |
|
29 |
0 |
1 |
0 |
0 |
1 |
0 |
6,768 |
83 |
1 |
1 |
0 |
0 |
1 |
0 |
6,928 |
|
30 |
0 |
1 |
0 |
0 |
1 |
0 |
6,745 |
84 |
1 |
1 |
0 |
0 |
1 |
0 |
6,951 |
|
31 |
0 |
1 |
0 |
0 |
1 |
0 |
6,802 |
85 |
1 |
1 |
0 |
0 |
1 |
0 |
6,932 |
|
32 |
0 |
1 |
0 |
0 |
1 |
0 |
6,757 |
86 |
1 |
1 |
0 |
0 |
1 |
0 |
6,952 |
|
33 |
0 |
1 |
0 |
0 |
0 |
1 |
6,808 |
87 |
1 |
1 |
0 |
0 |
1 |
0 |
6,908 |
|
34 |
0 |
1 |
0 |
0 |
0 |
1 |
6,851 |
88 |
1 |
1 |
0 |
0 |
0 |
1 |
7,042 |
|
35 |
0 |
1 |
0 |
0 |
0 |
1 |
6,908 |
89 |
1 |
1 |
0 |
0 |
0 |
1 |
7,071 |
|
36 |
0 |
1 |
0 |
0 |
0 |
1 |
6,824 |
90 |
1 |
1 |
0 |
0 |
0 |
1 |
7,080 |
|
37 |
0 |
1 |
0 |
0 |
0 |
1 |
6,846 |
91 |
1 |
1 |
0 |
0 |
0 |
1 |
6,963 |
|
38 |
0 |
0 |
1 |
0 |
0 |
0 |
6,454 |
92 |
1 |
1 |
0 |
0 |
0 |
1 |
7,013 |
|
39 |
0 |
0 |
1 |
0 |
0 |
0 |
6,397 |
93 |
1 |
0 |
1 |
0 |
0 |
0 |
6,655 |
|
40 |
0 |
0 |
1 |
0 |
0 |
0 |
6,461 |
94 |
1 |
0 |
1 |
0 |
0 |
0 |
6,659 |
|
41 |
0 |
0 |
1 |
0 |
0 |
0 |
6,430 |
95 |
1 |
0 |
1 |
0 |
0 |
0 |
6,908 |
|
42 |
0 |
0 |
1 |
0 |
0 |
0 |
6,477 |
96 |
1 |
0 |
1 |
1 |
0 |
0 |
6,745 |
|
43 |
0 |
0 |
1 |
0 |
0 |
0 |
6,465 |
97 |
1 |
0 |
1 |
1 |
0 |
0 |
6,757 |
|
44 |
0 |
0 |
1 |
1 |
0 |
0 |
6,802 |
98 |
1 |
0 |
1 |
1 |
0 |
0 |
6,764 |
|
45 |
0 |
0 |
1 |
1 |
0 |
0 |
6,607 |
99 |
1 |
0 |
1 |
1 |
0 |
0 |
6,733 |
|
46 |
0 |
0 |
1 |
1 |
0 |
0 |
6,551 |
100 |
1 |
0 |
1 |
1 |
0 |
0 |
6,721 |
|
47 |
0 |
0 |
1 |
0 |
1 |
0 |
6,671 |
101 |
1 |
0 |
1 |
0 |
1 |
0 |
6,802 |
|
48 |
0 |
0 |
1 |
0 |
1 |
0 |
6,659 |
102 |
1 |
0 |
1 |
0 |
1 |
0 |
7,056 |
|
49 |
0 |
0 |
1 |
0 |
1 |
0 |
6,633 |
103 |
1 |
0 |
1 |
0 |
1 |
0 |
6,835 |
|
50 |
0 |
0 |
1 |
0 |
1 |
0 |
6,721 |
104 |
1 |
0 |
1 |
0 |
1 |
0 |
6,846 |
|
51 |
0 |
0 |
1 |
0 |
1 |
0 |
6,620 |
105 |
1 |
0 |
1 |
0 |
0 |
1 |
6,957 |
|
52 |
0 |
0 |
1 |
0 |
0 |
1 |
6,697 |
106 |
1 |
0 |
1 |
0 |
0 |
1 |
6,685 |
|
53 |
0 |
0 |
1 |
0 |
0 |
1 |
6,733 |
107 |
1 |
0 |
1 |
0 |
0 |
1 |
6,802 |
|
54 |
0 |
0 |
1 |
0 |
0 |
1 |
6,768 |
108 |
1 |
0 |
1 |
0 |
0 |
1 |
6,908 |
-
2.1.2. Расчет коэффициентов логарифмической (линеаризованной) модели
Расчет коэффициентов модели (4) осуществляется на компьютере с помощью пакета прикладных программ. Так, например, в среде MS EXCEL в пакете Анализ данных 3 имеется функция Регрессия , позволяющая получить значения коэффициентов модели (4)4.
Для расчета коэффициентов модели в качестве входного интервала Y нужно указать столбец, содержащий данные о логарифмах цен, а в качестве входного интервала X – указать массив данных обо всех ценообразующих факторах таблицы 6. После нажатия кнопки ОК на экране под рубрикой ВЫВОД ИТОГОВ выводится информация о показателях статистической надежности модели (4) и значениях ее коэффициентов в виде трех таблиц (таблицы 7–9).
Таблица 7
Регрессионная статистика
|
Множественный R |
0,940764055 |
|
R-квадрат |
0,885037007 |
|
Нормированный R-квадрат |
0,878207522 |
|
Стандартная ошибка |
0,058649088 |
|
Наблюдения |
108 |
Таблица 8
Дисперсионный анализ 5
|
(вариация результата y) |
df (число степеней свободы) |
SS (сумма квадратов отклонений) |
MS (дисперсия на одну степень свободы) |
F (расчетное значение F критерия) |
Значимость F (уровень значимости) |
|
Регрессия (факторная) |
6 |
2,674528704 |
0,445754784 |
129,5905971 |
3,84798E-45 |
|
Остаток (остаточная) |
101 |
0,347411264 |
0,003439715 |
||
|
Итого (общая) |
107 |
3,021939968 |
Таблица 9
Параметры (коэффициенты) модели и их статистические характеристики
|
Переменная |
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-значение |
Нижние 95 % |
Верхние 95 % |
|
Y-пересечение |
6,67512101 |
0,0140681 |
474,484487 |
6,438E-171 |
6,647213 |
6,7030284 |
|
Переменная X1 |
0,17764388 |
0,0113461 |
15,6568170 |
9,082E-29 |
0,1551362 |
0,2001515 |
|
Переменная X2 |
-0,09172776 |
0,0137750 |
-6,6589795 |
1,462E-09 |
-0,1190537 |
-0,0644017 |
|
Переменная X3 |
-0,19385414 |
0,0137647 |
-14,083416 |
1,438E-25 |
-0,2211596 |
-0,1665486 |
|
Переменная X4 |
0,09118724 |
0,0167850 |
5,43266185 |
3,852E-07 |
0,0578903 |
0,1244841 |
|
Переменная X5 |
0,19212105 |
0,0154272 |
12,4533179 |
3,979E-22 |
0,1615174 |
0,2227246 |
|
Переменная X6 |
0,25851685 |
0,0157248 |
16,4399769 |
2,599E-30 |
0,2273229 |
0,2897108 |
3 Прежде чем воспользоваться этим программным обеспечением, необходимо проверить доступ к нему. Для этого в главном меню надо последовательно выбрать Сервис/Надстройки и установить флажок Пакет анализа . Если при установке офиса была использована конфигурация по умолчанию, то Excel потребует установочный диск.
4 Необходимо помнить, что MS Excel имеет ограничения по количеству входных данных. Так, например, он позволяет строить регрессионные модели с количеством независимых входных переменных, не превышающим число 16. Если количество переменных больше 16, необходимо задействовать другие стандартные пакеты прикладных программ, например ППП Manugistics StatGraphics Plus 5.1 Enterprise. Другим выходом является переход к моделям с количественными и квазиколичественными факторами, рассмотрение которых выходит за рамки настоящих рекомендаций.
5 Светлым курсивным шрифтом в скобках даны принятые в отечественной литературе наименования параметров.
Для удобства восприятия результатов расчета представим таблицу 9 в измененном виде, раскрыв конкретные названия факторов модели и сократив количество значащих цифр.
Таблица 10
Параметры (коэффициенты) модели и их статистические характеристики
|
Переменная |
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-значение |
Нижние 95 % |
Верхние 95 % |
|
Свободный член |
6,6751 |
0,0141 |
474,4845 |
6,438E-171 |
6,6472 |
6,6751 |
|
Х1 = зона 2 |
0,1776 |
0,0113 |
15,6568 |
9,082E-29 |
0,1551 |
0,1776 |
|
Х2 = блочный дом |
-0,0917 |
0,0138 |
-6,6590 |
1,462E-09 |
-0,1191 |
-0,0917 |
|
Х3 = деревянный дом |
-0,1939 |
0,0138 |
-14,0834 |
1,438E-25 |
-0,2212 |
-0,1939 |
|
Х4 = 2-комнатная квартира |
0,0912 |
0,0168 |
5,4327 |
3,852E-07 |
0,0579 |
0,0912 |
|
Х5 = 3-комнатная квартира |
0,1921 |
0,0154 |
12,4533 |
3,979E-22 |
0,1615 |
0,1921 |
|
Х6 = 4-комнатная квартира |
0,2585 |
0,0157 |
16,4400 |
2,599E-30 |
0,2273 |
0,2585 |
В третьей строке таблицы 7 для логарифмической модели представлено значение нормированного коэффициента детерминации R-квадрат = 0,878, скорректированного на число степеней свободы (учитывающее объем выборки и количество независимых переменных). Этот коэффициент говорит о том, что модель (4) объясняет приблизительно 88 процентов вариации логарифмов цен на рынке жилой недвижимости конкретного поселения при вариации по всей выборке логарифмов учтенных в модели факторов. По величине этого показателя нельзя напрямую сравнивать качество линейных и линеаризованных (как в нашем случае) регрессионных моделей, поэтому в дальнейшем (см. п. 2.1.5) значение коэффициента детерминации рассчитывается в исходных координатах рыночных цен и их модельных оценок. На практике в качестве минимального (критического) значения этого коэффициента обычно принимают значение, равное 0,7.
Оценку надежности уравнения регрессии в целом и показателя тесноты связи ( множественный R – первая строка таблицы 7) проводят с помощью F-критерия Фишера. Его расчетное значение должно быть больше критического (табличного)6. Обычно критическое значение F-критерия для объема выборки более чем 100 наблюдений находится на уровне 2–3 единиц7. Расчетное значение критерия Фишера для логарифмической модели (4) представлено в 5-м столбце таблицы 8: F-расчетное = 129,59. Оно на порядки больше критического значения. Вероятность случайно получить такое значение F-критерия (см. 6-й столбец таблицы 8: значимость F ) составляет бесконечно малую величину 3,848 х 10-45. Уровень вероятности, с которой модель можно считать статистически значимой, определяется вычитанием из единицы значения значимости F . В общем случае для того чтобы модель (4) считалась статистически надежной, например с не менее чем 95-процентной вероятностью, необходимо, чтобы выполнялось неравенство:
Значимость F ≤ 0,05.
Если принять статистическую значимость на уровне 90 процентов, то нужно добиваться выполнения неравенства:
Значимость F ≤ 0,1.
Кроме проверки значимости регрессионного уравнения в целом, целесообразно выполнить оценку надежности получения отдельных коэффициентов модели. Другим словами, необходимо проверить статистическую надежность выявленной связи между моделируемой величиной (средней ценой объекта) и конкретным влияющим фактором. В таблицах 9 и 10 представлена информация о значимости коэффициентов рассматриваемой модели, оцененной с помощью t-критерия Стьюдента 8. Для того чтобы каждый коэффициент модели считался значимым, необходимо, чтобы абсолютное значение t-статистики для этого коэффициента (столбец 4 таблиц 9 и 10) превышало критическое значение9. В столбце 5 таблицы 9 представлен уровень значимости значений коэффициентов модели в долях единицы ( Р-значение ). Если этот показатель меньше принятого уровня (обычно 0,05; это соответствует надежности принятия решения с 5-процентной вероятностью ошибки), делают вывод о неслучайной природе данного значения коэффициента, то есть о том, что он статистически значим и надежен. Для того чтобы коэффициент, например с не менее чем 90-процентной вероятностью, считался статистически надежным, необходимо, чтобы уровень значимости P-значение ≤ 0,1 .
Следует обращать внимание на совпадение знаков оценок границ доверительного интервала для значений коэффициентов регрессионной модели (столбцы 6 и 7 таблиц 9 и 10). Если знаки величин Нижние 95 % и Верхние 95 % , являющихся границами доверительного интервала для коэффициента модели, различаются, это означает, что доверительный интервал включает в себя нулевое значение проверяемого коэффициента. Такой случай необходимо рассматривать как необоснованное включение факторного признака в состав основных влияющих факторов модели и проводить объединение данной группы (или градации) с ближайшей к ней по величине коэффициента модели. При этом расчет коэффициентов модели необходимо провести заново.
В рассматриваемом примере значимость всех влияющих факторов не вызывает сомнений, однако практика показывает, что в условиях ограниченного объема рыночной информации, надежность которой также не абсолютна, получить высокие показатели надежности иногда бывает достаточно сложно. Поэтому при построении моделей оценки стоимости недвижимости статистическую надежность уравнения регрессии в целом и отдельных его коэффициентов на уровне 80 процентов можно считать приемлемой.
Соответствие перечисленным критериям является необходимым условием построения корректных регрессионных моделей оценки стоимости. Несоответствие может быть следствием многих причин, главными из которых являются следующие: неправильный выбор ценообразующих факторов, недостоверность информации, недостаточность объема экспериментальной выборки. В любом случае, если соответствие критериям не обеспечивается, перед тем как рассчиты- вать коэффициенты, нужно попытаться устранить эти причины. В частности, корректность выбора экспертами ценообразующих факторов и представление их в цифровом виде можно попытаться проверить с использованием формальных математических подходов (см. п. 3).
-
2.1.3. Расчет коэффициентов исходной мультипликативной модели регрессии
-
2.1.4. Расчет стоимости квартир с помощью регрессионной модели оценки
В таблицах 9 и 10 показаны результаты оценок коэффициентов модели (4): Ln a0 , Ln a1 , Ln a2 , …, Ln a6 . Для того чтобы перейти собственно к параметрам a0 , a1 , a2 , …, a6 модели (3) необходимо полученные значения преобразовать (потенцировать), взяв от них экспоненту.
После такого преобразования получим следующее выражение для оценки стоимости недвижимости методом массовой оценки:
. (5)
Из уравнения (5) модели следует, что стоимость одного квадратного метра эталонной квартиры (однокомнатной квартиры, находящейся в кирпичном доме в первой ценовой зоне) равна 792,44 денежных единиц (д. е.)
Квартиры, находящиеся во второй ценовой зоне, дороже эталонной на 19 процентов (параметр 1,194). Квартиры, расположенные в блочном доме, на 9 процентов дешевле таких же квартир, расположенных в кирпичных домах (параметр 0,912). Квартиры, расположенные в деревянном доме, на 18 процентов дешевле аналогичных квартир, расположенных в кирпичных домах (параметр 0,824). Четырехкомнатные квартиры дороже одно-, двух- и трехкомнатных квартир10 и т. д.
Расчетные значения стоимости единицы общей площади оцениваемых квартир получены по формуле (5) с использованием значений переменных, представленных в таблице 6.
Так, например, для объекта № 7 (зона 2, кирпичный дом, 1-комнатная квартира) x1 = 0, x2 = 0, x3 = 0, x4 = 1, x5 = 0, x6 = 0.
У = 792,44 х 1,194° х 0,912° х 0,824° х 1,0951 х 1,212° х 1,295° = 792,44 х 1,095 = 868 д. е.
Для объекта № 55 (зона 1, деревянный дом, 4-комнатная квартира) x1 = 0, x2 = 0, x3 = 1, x4 = 0, x5 = 0, x6 = 1.
У = 792,44 х 1,194° х 0,912° х 0,8241 х 1,095° х 1,212° х 1,2951 = 792,44 х 0,824 х 1,295 = 846 д. е.
Для объекта № 87 (зона 2, блочный дом, 3-комнатная квартира) x1 = 1, x2 = 1, x3 = 0, x4 = 0, x5 = 1, x6 = 0.
у = 792,44x1,1941х0,9121х0,824°х1,095°х1,2121х1,295° = 792,44 х 1,194 х 0,912 х 1,212 = 1 046 д. е.
Результаты расчета рыночных стоимостей оцениваемых квартир представлены в таблице 11. В этой же таблице приведены значения отношения вычисленной оценки стоимости к цене объекта на рынке, необходимые для дальнейшего рассмотрения.
Таблица 11
|
& s 5 |
2 04 1 n |
Дом |
Квартира |
s S |
5 |
81 6 ? |
& s S |
2 04 n |
Дом |
Квартира |
s |
5 |
81 6 ? |
||||||
|
‘S I 3 6 |
‘S Q. Q) |
I i 3 04 |
i 2 § co |
I i 3 4 |
‘S I 3 6 |
‘S Q. Q) 4 |
i 3 04 |
i 3 co |
! i 3 4 |
||||||||||
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
800 |
792 |
0,99 |
55 |
0 |
0 |
1 |
0 |
0 |
1 |
840 |
846 |
1,01 |
|
2 |
0 |
0 |
0 |
0 |
0 |
0 |
802 |
792 |
0,99 |
56 |
0 |
0 |
1 |
0 |
0 |
1 |
860 |
846 |
0,98 |
|
3 |
0 |
0 |
0 |
0 |
0 |
0 |
750 |
792 |
1,06 |
57 |
1 |
0 |
0 |
0 |
0 |
0 |
960 |
946 |
0,99 |
|
4 |
0 |
0 |
0 |
0 |
0 |
0 |
760 |
792 |
1,04 |
58 |
1 |
0 |
0 |
0 |
0 |
0 |
962 |
946 |
0,98 |
|
5 |
0 |
0 |
0 |
0 |
0 |
0 |
798 |
792 |
0,99 |
59 |
1 |
0 |
0 |
0 |
0 |
0 |
912 |
946 |
1,04 |
|
6 |
0 |
0 |
0 |
0 |
0 |
0 |
804 |
792 |
0,99 |
60 |
1 |
0 |
0 |
0 |
0 |
0 |
958 |
946 |
0,99 |
|
7 |
0 |
0 |
0 |
1 |
0 |
0 |
880 |
868 |
0,99 |
61 |
1 |
0 |
0 |
0 |
0 |
0 |
966 |
946 |
0,98 |
|
8 |
0 |
0 |
0 |
1 |
0 |
0 |
805 |
868 |
1,08 |
62 |
1 |
0 |
0 |
1 |
0 |
0 |
850 |
1036 |
1,22 |
|
9 |
0 |
0 |
0 |
1 |
0 |
0 |
860 |
868 |
1,01 |
63 |
1 |
0 |
0 |
1 |
0 |
0 |
1033 |
1036 |
1,00 |
|
10 |
0 |
0 |
0 |
1 |
0 |
0 |
880 |
868 |
0,99 |
64 |
1 |
0 |
0 |
1 |
0 |
0 |
1050 |
1036 |
0,99 |
|
11 |
0 |
0 |
0 |
0 |
1 |
0 |
965 |
960 |
0,99 |
65 |
1 |
0 |
0 |
0 |
1 |
0 |
1158 |
1147 |
0,99 |
|
12 |
0 |
0 |
0 |
0 |
1 |
0 |
989 |
960 |
0,97 |
66 |
1 |
0 |
0 |
0 |
1 |
0 |
1166 |
1147 |
0,98 |
|
13 |
0 |
0 |
0 |
0 |
1 |
0 |
910 |
960 |
1,05 |
67 |
1 |
0 |
0 |
0 |
1 |
0 |
1188 |
1147 |
0,97 |
|
14 |
0 |
0 |
0 |
0 |
1 |
0 |
990 |
960 |
0,97 |
68 |
1 |
0 |
0 |
0 |
1 |
0 |
1122 |
1147 |
1,02 |
|
15 |
0 |
0 |
0 |
0 |
1 |
0 |
960 |
960 |
1,00 |
69 |
1 |
0 |
0 |
0 |
1 |
0 |
1133 |
1147 |
1,01 |
|
16 |
0 |
0 |
0 |
0 |
1 |
0 |
969 |
960 |
0,99 |
70 |
1 |
0 |
0 |
0 |
0 |
1 |
1280 |
1225 |
0,96 |
|
17 |
0 |
0 |
0 |
0 |
0 |
1 |
1050 |
1026 |
0,98 |
71 |
1 |
0 |
0 |
0 |
0 |
1 |
1270 |
1225 |
0,96 |
|
18 |
0 |
0 |
0 |
0 |
0 |
1 |
1068 |
1026 |
0,96 |
72 |
1 |
0 |
0 |
0 |
0 |
1 |
1260 |
1225 |
0,97 |
|
19 |
0 |
0 |
0 |
0 |
0 |
1 |
1058 |
1026 |
0,97 |
73 |
1 |
0 |
0 |
0 |
0 |
1 |
1200 |
1225 |
1,02 |
|
20 |
0 |
0 |
0 |
0 |
0 |
1 |
1050 |
1026 |
0,98 |
74 |
1 |
0 |
0 |
0 |
0 |
1 |
1260 |
1225 |
0,97 |
|
21 |
0 |
1 |
0 |
0 |
0 |
0 |
713 |
723 |
1,01 |
75 |
1 |
1 |
0 |
0 |
0 |
0 |
870 |
863 |
0,99 |
|
22 |
0 |
1 |
0 |
0 |
0 |
0 |
715 |
723 |
1,01 |
76 |
1 |
1 |
0 |
0 |
0 |
0 |
840 |
863 |
1,03 |
|
23 |
0 |
1 |
0 |
0 |
0 |
0 |
727 |
723 |
0,99 |
77 |
1 |
1 |
0 |
0 |
0 |
0 |
850 |
863 |
1,02 |
|
24 |
0 |
1 |
0 |
0 |
0 |
0 |
740 |
723 |
0,98 |
78 |
1 |
1 |
0 |
0 |
0 |
0 |
880 |
863 |
0,98 |
|
25 |
0 |
1 |
0 |
1 |
0 |
0 |
780 |
791 |
1,01 |
79 |
1 |
1 |
0 |
1 |
0 |
0 |
970 |
945 |
0,97 |
|
26 |
0 |
1 |
0 |
1 |
0 |
0 |
810 |
791 |
0,98 |
80 |
1 |
1 |
0 |
1 |
0 |
0 |
960 |
945 |
0,98 |
|
27 |
0 |
1 |
0 |
1 |
0 |
0 |
788 |
791 |
1,00 |
81 |
1 |
1 |
0 |
1 |
0 |
0 |
930 |
945 |
1,02 |
|
28 |
0 |
1 |
0 |
0 |
1 |
0 |
880 |
876 |
1,00 |
82 |
1 |
1 |
0 |
1 |
0 |
0 |
955 |
945 |
0,99 |
|
29 |
0 |
1 |
0 |
0 |
1 |
0 |
870 |
876 |
1,01 |
83 |
1 |
1 |
0 |
0 |
1 |
0 |
1020 |
1046 |
1,03 |
|
30 |
0 |
1 |
0 |
0 |
1 |
0 |
850 |
876 |
1,03 |
84 |
1 |
1 |
0 |
0 |
1 |
0 |
1044 |
1046 |
1,00 |
|
31 |
0 |
1 |
0 |
0 |
1 |
0 |
900 |
876 |
0,97 |
85 |
1 |
1 |
0 |
0 |
1 |
0 |
1025 |
1046 |
1,02 |
|
32 |
0 |
1 |
0 |
0 |
1 |
0 |
860 |
876 |
1,02 |
86 |
1 |
1 |
0 |
0 |
1 |
0 |
1045 |
1046 |
1,00 |
|
33 |
0 |
1 |
0 |
0 |
0 |
1 |
905 |
936 |
1,03 |
87 |
1 |
1 |
0 |
0 |
1 |
0 |
1000 |
1046 |
1,05 |
|
34 |
0 |
1 |
0 |
0 |
0 |
1 |
945 |
936 |
0,99 |
88 |
1 |
1 |
0 |
0 |
0 |
1 |
1144 |
1117 |
0,98 |
|
35 |
0 |
1 |
0 |
0 |
0 |
1 |
1000 |
936 |
0,94 |
89 |
1 |
1 |
0 |
0 |
0 |
1 |
1177 |
1117 |
0,95 |
|
36 |
0 |
1 |
0 |
0 |
0 |
1 |
920 |
936 |
1,02 |
90 |
1 |
1 |
0 |
0 |
0 |
1 |
1188 |
1117 |
0,94 |
|
37 |
0 |
1 |
0 |
0 |
0 |
1 |
940 |
936 |
1,00 |
91 |
1 |
1 |
0 |
0 |
0 |
1 |
1057 |
1117 |
1,06 |
|
38 |
0 |
0 |
1 |
0 |
0 |
0 |
635 |
653 |
1,03 |
92 |
1 |
1 |
0 |
0 |
0 |
1 |
1111 |
1117 |
1,01 |
|
39 |
0 |
0 |
1 |
0 |
0 |
0 |
600 |
653 |
1,09 |
93 |
1 |
0 |
1 |
0 |
0 |
0 |
777 |
780 |
1,00 |
|
40 |
0 |
0 |
1 |
0 |
0 |
0 |
640 |
653 |
1,02 |
94 |
1 |
0 |
1 |
0 |
0 |
0 |
780 |
780 |
1,00 |
|
41 |
0 |
0 |
1 |
0 |
0 |
0 |
620 |
653 |
1,05 |
95 |
1 |
0 |
1 |
0 |
0 |
0 |
1000 |
780 |
0,78 |
|
42 |
0 |
0 |
1 |
0 |
0 |
0 |
650 |
653 |
1,00 |
96 |
1 |
0 |
1 |
1 |
0 |
0 |
850 |
854 |
1,00 |
|
43 |
0 |
0 |
1 |
0 |
0 |
0 |
642 |
653 |
1,02 |
97 |
1 |
0 |
1 |
1 |
0 |
0 |
860 |
854 |
0,99 |
|
44 |
0 |
0 |
1 |
1 |
0 |
0 |
900 |
715 |
0,79 |
98 |
1 |
0 |
1 |
1 |
0 |
0 |
866 |
854 |
0,99 |
|
45 |
0 |
0 |
1 |
1 |
0 |
0 |
740 |
715 |
0,97 |
99 |
1 |
0 |
1 |
1 |
0 |
0 |
840 |
854 |
1,02 |
|
46 |
0 |
0 |
1 |
1 |
0 |
0 |
700 |
715 |
1,02 |
100 |
1 |
0 |
1 |
1 |
0 |
0 |
830 |
854 |
1,03 |
|
47 |
0 |
0 |
1 |
0 |
1 |
0 |
789 |
791 |
1,00 |
101 |
1 |
0 |
1 |
0 |
1 |
0 |
900 |
945 |
1,05 |
|
48 |
0 |
0 |
1 |
0 |
1 |
0 |
780 |
791 |
1,01 |
102 |
1 |
0 |
1 |
0 |
1 |
0 |
1160 |
945 |
0,81 |
|
49 |
0 |
0 |
1 |
0 |
1 |
0 |
760 |
791 |
1,04 |
103 |
1 |
0 |
1 |
0 |
1 |
0 |
930 |
945 |
1,02 |
|
50 |
0 |
0 |
1 |
0 |
1 |
0 |
830 |
791 |
0,95 |
104 |
1 |
0 |
1 |
0 |
1 |
0 |
940 |
945 |
1,01 |
|
51 |
0 |
0 |
1 |
0 |
1 |
0 |
750 |
791 |
1,05 |
105 |
1 |
0 |
1 |
0 |
0 |
1 |
1050 |
1010 |
0,96 |
|
52 |
0 |
0 |
1 |
0 |
0 |
1 |
810 |
846 |
1,04 |
106 |
1 |
0 |
1 |
0 |
0 |
1 |
800 |
1010 |
1,26 |
|
53 |
0 |
0 |
1 |
0 |
0 |
1 |
840 |
846 |
1,01 |
107 |
1 |
0 |
1 |
0 |
0 |
1 |
900 |
1010 |
1,12 |
|
54 |
0 |
0 |
1 |
0 |
0 |
1 |
870 |
846 |
0,97 |
108 |
1 |
0 |
1 |
0 |
0 |
1 |
1000 |
1010 |
1,01 |
Как следует из анализа полученных расчетных данных, среднее по всей выборке значение отношения «оценка/цена» составляет 1,00, минимальное значение – 0,78 (объект № 95), максимальное – 1,26 (объект № 106). Из 108 объектов выборки оценка превышает цену у 54 объектов и не превышает (равна и ниже) ее – также у 54 объектов.
-
2.1.5. Оценка качества регрессионной модели оценки
Оценку качества модели (5) выполним на основе данных о разности реальных значений цен и их оценок (в терминах статистики – остатков) по модели (5) с помощью следующих показателей11:
-
• коэффициент детерминации;
-
• обобщенная ошибка модели оценки;
-
• средняя ошибка аппроксимации;
-
• результаты анализа распределения остатков модели.
Оценка коэффициента детерминации
Коэффициент детерминации является одной из обобщенных мер качества модели оценки. Он показывает, какую долю изменения рыночных цен объясняют факторы, включенные в модель оценки, и рассчитывается по формуле:
n
К у , - У i ) 2
R 2 = 1 — -----—, (6)
К ( у , - У ) , =1
где yi – реальное значение удельной цены;
y ˆ i – вычисленное по модели значение удельной цены (расчетная цена продажи, то есть оценка рыночной стоимости);
y – среднее значение реальных цен;
n – количество наблюдений реальных цен.
На основе данных таблицы 11 рассчитаем значение коэффициента детерминации:
108 108 2
— 0, 005 •
К ( y i - У1 ) 2 = 293 558; К ( у , - У ) = 2 528 676 • Отсюда R 2 = 1 -
, =1
, =1
Для корректного сравнения оценок качества различных моделей целесообразно использовать нормированный коэффициент детерминации, скорректированный на число степеней свободы (конечного объема выборки n и числа независимых переменных в уравнении регрессии m ). В данном случае n = 108, m = 6 (1 зона + 2 типа стен + 3 типа квартир), отсюда:
RK0 2 = 1 - (1 - R 2) х ( n - 1) = 1 - (1 - 0,885) х 108 - 1 = 0,878 12 .
корр v ' ( n - m -1) v ' 108 - 6 -1
Это означает, что регрессионная модель (5) оценки стоимости примерно на 88 процентов объясняет изменение цен в экспериментальной выборке. Оставшиеся 12 процентов вариации цен выборки обусловлены не учитываемыми моделью факторами.
На практике в качестве минимального (критического) значения данного коэффициента принимают значение, равное 0,7.
Обобщенная оценка ошибки модели
Обобщенная ошибка регрессионной модели вида (3), позволяющая проводить сравнение с другими моделями, рассчитывается как выборочное среднеквадратическое отклонение (СКО) по формуле:
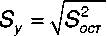
где S о 2 ст
n
Е ( y - y ) 2
i=1___________________ n - m -1
– выборочная дисперсия ошибки регрессионной модели;
Кодировка ценообразующих факторов
Кодировка факторов для аддитивной «логарифмической» модели
Рыночные цены и рассчитанные по регрессионной модели стоимости квартир экспериментальной выборки
n – общее количество наблюдений в экспериментальной выборке; m – число независимых переменных в уравнении регрессии.
В рассматриваемом случае n = 108, m = 6. Отметим, что данные о числе степеней свободы модели приведены в таблице 8, сформированной функцией Регрессия MS Excel.
На основе данных таблицы 11 рассчитаем значение выборочной дисперсии:
2 S ост
n
Е ( y - y ) 2
= i=1______________ n - m -1
108 - 6 -1
= 2 891
Отсюда следует, что ошибка оценки Sy = V2891 = 53,8 д. е.
Более удобным для сравнения моделей является показатель относительной ошибки модели – коэффициент вариации:
S = f rх 100% = 53,8х 100% = 5,9% .
y y 917
Оценка средней ошибки аппроксимации
Средняя ошибка аппроксимации13 отражает свойства модели по воспроизведению исходных рыночных данных и рассчитывается по формуле:
А = А отн = -Е ।y - y i^ х 100 %. (8)
nt! Yi
В таблице 12 приведена принятая в отечественной литературе характеристика точности модели оценки в зависимости от значения данного показателя.
Таблица 12
Характеристики точности эконометрических моделей по уровню средней ошибки аппроксимации
|
Значение ошибки А отн |
Характеристика точности модели |
|
до 7 % |
Высокая точность |
|
7–12 % |
Хорошая точность |
|
12–15 % |
Удовлетворительная точность |
|
свыше 15 % |
Неудовлетворительная точность |
Средняя ошибка аппроксимации модели оценки, реализующей метод множественной регрессии, рассчитанная на основе данных таблицы 11 по формуле (8), равна 3,3 процента, что, как следует из таблицы 12, соответствует высокой точности оценки.
Анализ распределения остатков модели
На основе данных таблицы 11 с помощью Мастера диаграмм ППП MS Excel построим гистограмму частот отношений «оценка/цена» в исходных координатах (рис. 1) и в стандартизованных (сдвинутых на величину среднего значения и выраженного в долях СКО) координатах (рис. 2).
|
Карман |
Частота |
|
0,78 |
1 |
|
0,83 |
2 |
|
0,88 |
0 |
|
0,92 |
0 |
|
0,97 |
16 |
|
1,02 |
65 |
|
1,07 |
19 |
|
1,12 |
2 |
|
1,17 |
1 |
|
1,21 |
0 |
|
Еще |
2 |
|
ИТОГО |
108 |
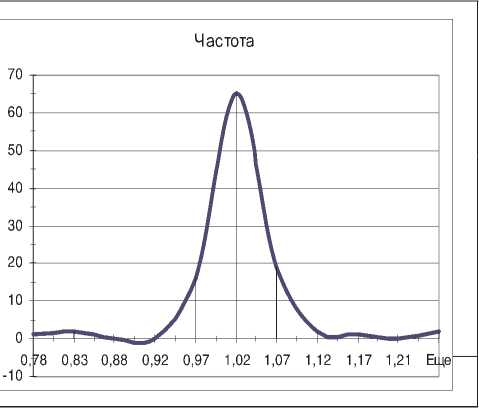
Рис. 1. Гистограмма частот отношений «оценка/цена» многомерной регрессионной модели
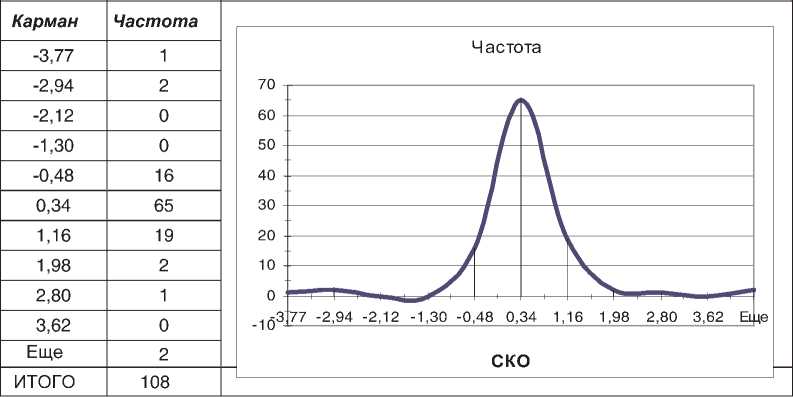
Рис. 2. Стандартизованная гистограмма частот отношений «оценка/цена» многомерной регрессионной модели
Из рисунков видно, что распределение частот отношений «оценка/цена» является одномодальным и имеет близкие к симметричным затухающие «крылья». Величина моды (значение переменной, соответствующее максимуму кривой распределения)14 незначительно отличается от среднего по выборке отношения (1,00). Это свидетельствует о том, что оцениваемые моделью средние значения цен хорошо соответствуют наиболее вероятным значениям, то есть рыночным стоимостям объектов.
Сравнивая вид огибающей гистограммы распределения ошибок модели в стандартизованных координатах (рис. 2) с кривой плотности стандартного нормального распределения, можно сделать выводе о приемлемой близости этих кривых. Это означает, что предпосылки регрессии можно считать выполненными и можно в полной мере доверять построенной модели.
Необходимо отметить и отличие – присутствие в выборке значений, отстоящих более чем на ± 3,5 СКО от центра группирования. В таблице 11 к таким выделяющимся объектам можно отнести цены на квартиры с номерами наблюдений 62, 106, с одной стороны, и 95, 44 – с другой.
На такие объекты необходимо обращать дополнительное внимание с целью уточнения исходных данных по ним. В ряде случаев после уточнения информации о таких объектах, они выводятся из состава выборки как включенные в нее ошибочно из-за неучета характеристик, резко выделяющих их из группы оцениваемых объектов. Такими объектами могут быть, например, квартиры с недавно выполненным ремонтом с использованием современных материалов, существенно повышающим стоимость, или, наоборот, квартиры в чрезвычайно плохом состоянии или в ветхих домах.
На практике необходимо либо уточнить информацию об этих квартирах и отнести их в иную, соответствующую их параметрам группу, либо оценивать такие квартиры для налогообложения индивидуальным образом (методами индивидуальной оценки). В любом из этих случаев следует пересчитать коэффициенты рассматриваемой модели.
-
2.1.6. Определение величины коэффициента налоговой оценки Kн
Как уже отмечалось, для минимизации рисков апелляций со стороны налогоплательщиков налоговую стоимость целесообразно сделать меньше рыночной путем умножения последней на некий понижающий (налоговый) коэффициент.
Предлагается следующее правило определения величины этого коэффициента: налоговый коэффициент должен иметь такое значение, при котором обеспечивается заранее заданный р-процентный уровень превышения налоговой стоимости над рыночными ценами на исследуемом рынке недвижимости.
Под р-процентным уровнем превышения здесь понимается такое количество существенных превышений оценок над соответствующими рыночными ценами, которое соответствует заранее заданной в процентном отношении величине. Например, 3-процентный уровень превышения означает, что в выборке должно быть около 3-х процентов расчетных стоимостей, величины которых существенно больше соответствующих им рыночных цен. Иначе говоря, количество отношений «оценка/цена», превышающих существенный уровень, должно быть на уровне 3-х процентов от объема обрабатываемой выборки. Нестрогое равенство применяется здесь в силу конечных объемов обрабатываемых на практике выборок, вследствие чего отношение целых чисел может быть не кратно одному проценту.
При этом под существенным превышением стоимости над ценой будем понимать такое превышение, при котором отношение «оценка/цена» не меньше заранее заданной величины. Например, 5-процентное существенное превышение расчетных значений стоимостей над соответствующими значениями рыночных цен означает, что существенным превышением считается такое превышение, при котором стоимость на 5 и более процентов больше соответствующей рыночной цены. То есть отношение «оценка/цена» для существенного превышения составляет не меньше чем 1,05.
Использование понятия существенного превышения целесообразно в связи с тем, что незначительные превышения модельных значений над соответствующими рыночными ценами, скорее всего, не будут служить основанием для апелляций налогоплательщиков
(в том числе и в связи с конечной точностью альтернативной индивидуальной оценки), и контролировать необходимо количество тех превышений, при которых угроза апелляции расценивается как реальная.
Сформированная выборка объектов недвижимости является по определению репрезентативной, поэтому выборочная функция распределения исследуемой случайной величины (рыночных цен) должна быть близка аналогичной функции распределения по генеральной совокупности. Отсюда, налагая ограничения на уровень (относительное количество) и существенность «выбросов» модельных значений в выборке, можно ожидать сохранения заданных параметров и для генеральной совокупности.
Р-процентный уровень существенных превышений рекомендуется устанавливать в диапазоне 1–3 процента от общего объема экспериментальной выборки15. Существенными рекомендуется считать 5-процентные превышения (оценка/цена > 1,05).
Алгоритм расчета налогового коэффициента при этом выглядит следующим образом:
-
1) полученные по выборке значения отношений «оценка/цена» сортируются по убыванию (возможно использование инструмента Данные , Сортировка пакета MS Excel);
-
2) анализируется наличие и количество существенных превышений («оценка/цена» > 1,05);
-
3) рассчитывается фактический уровень существенных превышений как отношение числа таких превышений к объему выборки, затем полученное значение сопоставляется с заранее заданным р-процентным уровнем превышений.
Если фактический уровень существенных превышений больше заданного, проводится расчет понижающего коэффициента налоговой оценки, в противном случае налоговый коэффициент принимается равным Кн = 1.
Для расчета коэффициента налоговой оценки Кн меньшего единицы:
-
4) анализируются объекты со значениями отношения «оценка/цена», входящими в группу с р-процентным уровнем превышений. Отбирается минимальное значение превышения «оценка/цена» ( Кпрmin ) в данной группе существенных превышений;
-
5) фиксируется максимальное значение превышения «оценка/цена» ( Кпрmax ) в остальной выборке;
-
6) рассчитывается значение налогового коэффициента Кн р% из соотношения: Кн р% х Кпрmax = 1;
-
7) проводится анализ уровня превышений модельных значений, полученных с учетом понижающего коэффициента, над рыночными ценами. Проверяется выполнение заданного р-процентного уровня превышений (условие Кн р% х Knp min > 1,05). При необходимости значение налогового коэффициента уточняется.
Аналогом рассмотренной задачи в классическом построении регрессионных и других моделей может служить расчет границ доверительного интервала для рыночной стоимости объекта недвижимости как среднего значения цены единицы генеральной совокупности. Интервал, в пределах которого гарантируется нахождение оцененного по выборке среднего значения (стоимости), определяется для заданной доверительной вероятности. Таким образом, всегда предполагается некоторая вероятность выхода за пределы интервала, численно равная дополнению доверительной вероятности до 1 (100 %). Задавая уровень этой вероятности выхода, и зная закон распределении ошибок измерения рыночной стоимости, можно количественно определить границы доверительного интервала для ее значения.
Если, например, данные, на которых строится модель, подчинены нормальному закону распределения, то можно говорить, что ошибка модели с 95-процентной вероятностью не превышает границ ±1,96оy, а с вероятностью 99 процентов - ±2,58оy. В экономических за- дачах принято ориентироваться на 95-процентный доверительный интервал, соответствующий 5-процентному уровню превышений «оценка/цена», включая несущественные превышения. Учитывая это обстоятельство, налоговый коэффициент можно определить по нижней границе доверительного интервала на основе значения относительной ошибки модели (см. п. 2.1.5) : Кн2З = 1 - 1,96 х Зу.
Для рассматриваемого примера анализ данных расчета стоимости оцениваемых объектов (табл. 11) показывает, что в выборке имеется 12 объектов, отношение «оценка/цена» которых позволяет отнести их к категории объектов, имеющих существенное превышение стоимостей над ценами (значения стоимости превышают соответствующие значения цен в 1,05 и более раз). Максимальное значение превышения составляет 1,26 (объект № 106), предыдущие по величине значения превышения – 1,22 (объект № 62), 1,12 (объект № 107) и 1,09 (объект № 39).
При общем объеме выборки, равном 108 объектам, фактический уровень существенных превышений составляет 12/108 = 11 %, поэтому для выполнения рекомендаций по заранее заданному р-процентному уровню существенных превышений из диапазона 1–3 процента необходимо применить понижающий налоговый коэффициент16.
В рамках рекомендуемого диапазона (1–3 %) установим р-процентный уровень превышения в размере 2-х процентов (2-процентный уровень превышения). Тогда налоговый коэффициент, соответствующий этому уровню ( Кн2% ), необходимо рассчитать следующим образом.
Два процента от 108 объектов составляет 2 % х 108 = 2 объекта. Это значит, что после умножения на налоговый коэффициент модельных значений стоимости в числе существенных превышений должны остаться два объекта: объекты № 106 и № 62 с максимальными значениями отношения «оценка/цена», равными 1,26 и 1,22 соответственно. Отсюда следует, что расчет налогового коэффициента необходимо выполнять, ориентируясь на следующий за этими двумя объектами объект № 107, имеющий третье по величине отношение «оценка/цена» – 1,12.
Очевидно, что искомый налоговый коэффициент может быть найден из уравнения17:
1,12 х Кн2 % = 1.
Отсюда следует, что Кн2 % = 1/1,12 = 0,89 = 0,9.
Проверим выполнение заданного (2-процентного) уровня превышений. С учетом применения налогового коэффициента минимальное значение отношения «оценка/цена» в группе превышения должно быть не менее 1,05. Для объекта № 62 (1,22 х Кн2 % = 1,22 х 0,9 = 1,098) условие выполняется, следовательно, оно выполняется и для объекта № 106. Имеем два объекта с существенными превышениями оценок над ценами, остальные отношения не достигают порогового значения (1,05), то есть заданный 2-процентный уровень превышения обеспечивается.
Значение налогового коэффициента, рассчитанное на основе удвоенного значения относительной ошибки модели (в предположении о нормальности распределения) составляет Кн2 З = 1 - 1,96 х 0,059 = 0,88. Мы видим, что полученные двумя различными подходами оценки налогового коэффициента близки. Учитывая отклонения реального распределения от нормального (в частности, наличие маловероятных для данного объема выбор-
Таблица 13
Рыночные цены и налоговые стоимости квартир по регрессионной модели
В таблице 13 представлена информация о рыночных ценах на квартиры и соответствующих им налоговых стоимостях, полученных путем умножения расчетных значений рыночной стоимости на налоговый коэффициент 0,9. В этой же таблице приведены значения отношений налоговой стоимости и рыночной цены каждого объекта.
Как и ожидалось, в выборке рыночных цен и соответствующих им смоделированных значений налоговой стоимости имеются два объекта со значениями отношения «налоговая стоимость/цена», превышающими пороговое значение 1,05 (объекты № 106 – 1,14 и № 62 – 1,10). Еще один объект – № 107 имеет значение отношения 1,01. Значения налоговой стоимости для остальных объектов лежат ниже соответствующих им рыночных цен. Среднее по всей выборке значение отношения «налоговая стоимость/цена» составляет 0,901, минимальное значение – 0,70.
Расчеты показывают, что при применении значения налогового коэффициента Кн2% = 0,88 в выборке также остаются 2 объекта, для которых отношение «налоговая стои-мость/цена» превышает пороговое значение (№106 и № 62). Налоговые стоимости остальных объектов ниже рыночных. Среднее по всей выборке значение отношения «налоговая стоимость/цена» составляет 0,883, минимальное значение – 0,68.
-
2.1.7. Порядок определения базовых ставок и коэффициентов регрессионной модели
Ориентируясь на выражение (5), введем следующие обозначения:
С Б = 792,44 д. е.; K 1 = 1,194 x 1 ; K 2 = 0,912 x 2 х0,824 x 3 ; K 3 = 1,095 x 4 х 1,212 x 5 х 1,295 x 6 .
Тогда выражение (5) мультипликативной регрессионной модели можно представить в виде произведения обычных коэффициентов модели вида (1):
y = С к х К х Ко х К. .
Б 123
Заметим, что каждый из коэффициентов К 1– К 3 формируется сомножителями, количество которых численно равно количеству градаций соответствующего признака, уменьшенному на единицу. При этом свободный член уравнения – СБ определен для базового объекта, у которого зафиксированы по одной из «недостающих» градаций каждого признака.


