Оценка недвижимости для налогообложения
Автор: Грибовский С.В., Баринов Н.П.
Журнал: Имущественные отношения в Российской Федерации @iovrf
Рубрика: Блокнот практика
Статья в выпуске: 7 (58), 2006 года.
Бесплатный доступ
Короткий адрес: https://sciup.org/170151491
IDR: 170151491
Текст статьи Оценка недвижимости для налогообложения
С.В. Грибовский заместитель начальника ГУ «Городское управление инвентаризации и оценки недвижимости» (Санкт-Петербург), профессор, доктор экономических наук Н.П. Баринов генеральный директор ООО «Оценочная фирма «БОСИ» (Санкт-Петербург), старший научный сотрудник, кандидат технических наук
-
2.2. Модель кластерного анализа, основанная на методе параллельных сечений
Модели оценки стоимости, основанные на кластерном анализе, реализуются в рамках выражения, аналогичного общему виду модели оценки (1):
y = М д x E i x К 2 x Е з , (9)
где СБ – базовая ставка стоимости (стоимость 1 квадратного метра общей площади базового объекта оценки);
-
K1 – коэффициент местоположения;
-
K2 – коэффициент материала стен;
-
K3 – коэффициент количества комнат.
В рамках сформулированной постановки задачи2 рассмотрим алгоритмы построения двух кластерных мультипликативных моделей оценки стоимости:
-
• модели, основанной на методе параллельных сечений3;
-
• модели, основанной на методе последовательных сечений.
-
2.2.1. Расчет коэффициентов модели, основанной на методе параллельных сечений
Расчет базовой ставки стоимости
В методе параллельных сечений в качестве базовой ставки стоимости СБ берется средняя по всем объектам экспериментальной выборки цена 1 квадратного метра общей площади квартиры. Из таблицы 2 или 3 следует, что СБ = 917 денежных единиц (д. е.).
Расчет коэффициента местоположения ( K1 )
Значение коэффициента местоположения зависит от ценовой зоны. В методе параллельных сечений значение коэффициента местоположения ценовой зоны рассчитывается как отношение средней цены 1 квадратного метра общей площади всех находящихся в этой зоне объектов экспериментальной выборки, к средней по всей экспериментальной выборке цене 1 квадратного метра общей площади объекта недвижимости.
Используя данные таблицы 2 или 3, определим средние значения удельных цен объектов недвижимости ценовых зон. Среднее значение цен объектов 1-й зоны равно 835 д. е., 2-й – 1 005 д. е.
Эти данные позволяют рассчитать значения коэффициента местоположения (табл. 14).
Таблица 14
|
Номер ценовой зоны |
Значение K1 |
|
1 |
K 1 1 = 835/917 = 0,911 |
|
2 |
K1 2 = 1005/917 = 1,096 |
Расчет коэффициента материала стен ( K2 )
В соответствии с процедурой построения модели оценки стоимости, основанной на методе параллельных сечений, для расчета значений коэффициента материала стен по данным таблицы 2 необходимо предварительно рассчитать средние значения удельных цен по всем объектам экспериментальной выборки, имеющим идентичный материал стен. Среднее значение цен объектов, имеющих кирпичные стены, равно 997 д. е.; объектов, имеющих блочные стены, – 926 д. е.; объектов, имеющих деревянные стены, – 821 д. е.
Для расчета значений коэффициента материала стен необходимо поделить средние значения удельных цен объектов недвижимости, имеющих определенный материал стен, на среднее значения цен всех объектов недвижимости, находящихся в поселении (табл. 15).
Таблица 15
|
Стены |
Значение K2 |
|
Кирпичные |
K2 1 = 997/917 = 1,087 |
|
Из железобетонных блоков |
K2 2 = 926/917 = 1,010 |
|
Деревянные |
K 2 3 = 821/917 = 0,895 |
Расчет коэффициента количества комнат ( K3 )
В соответствии с процедурой построения модели оценки стоимости, основанной на методе параллельных сечений, для расчета значений коэффициента количества комнат на основе данных таблицы 2 необходимо предварительно рассчитать средние значения удельных цен объектов недвижимости, имеющих разное количество комнат. Это нужно сделать по данным всей экспериментальной выборки (по всем зонам и материалам стен вместе). Результаты этого расчета показаны в таблице 16.
Таблица 16
|
Количество комнат |
Среднее значение, д. е. |
|
1 |
791 |
|
2 |
870 |
|
3 |
963 |
|
4 |
1 030 |
Для расчета значений коэффициентов количества комнат необходимо поделить средние значения удельных цен объектов недвижимости, имеющих определенное количество комнат, на среднее значения удельных цен объектов недвижимости по всей выборке. Такой расчет показан в таблице 17.
Таблица 17
|
Количество комнат |
Значение К3 |
|
1 |
K 3 1 = 791/917 = 0,863 |
|
2 |
K3 2 = 870/917 = 0,949 |
|
3 |
K3 3 = 963/917 = 1,050 |
|
4 |
K3 4 = 1030/917 = 1,123 |
Примечание : Метод экспертных оценок выбора ценообразующих факторов и их оцифровки можно подкрепить использованием формальных процедур проверки статистической значимости различий средних значений цен по выбранным градациям признаков: местоположение – зона 1, зона 2; материал стен – кирпич, железобетонный блок, дерево и т. п. (см. п. 3).
-
2.2.2. Расчет стоимости квартир с помощью модели оценки, основанной на методе параллельных сечений
Расчетные значения стоимости единицы общей площади оцениваемых квартир получены по формуле (9) с использованием коэффициентов, представленных в таблицах 14, 15 и 17.
Так, например, для объекта № 1 (зона 1, кирпичный, однокомнатная):
У = Na x E 1 x K 1 x E 3 = 917 x 0,911 x 1,087 x 0,863 = 784 д. е.
Для объекта № 55 (зона 1, деревянный, 4-комнатная):
У = N x E x K 3 x E 4 = 917 x 0,911 x 0,895 x 1,123 = 840 д. е.
Для объекта № 87 (зона 2, блочный, 3-комнатная):
j? = N x E 2 x K 2 x E 3 = 917 x 1,096 x1,010 x 1,050 = 1 066 д. е.
Результаты расчета рыночных стоимостей оцениваемых квартир представлены в таблице 18. В этой же таблице приведены значения отношения вычисленной стоимости к цене объекта.
Среднее по всей выборке значение отношения «оценка/цена» составляет 1,00, минимальное – 0,78 (объект № 95), максимальное – 1,17 (объект № 106). Из 108 объектов выборки оценка превышает цену у 56 объектов и не превышает (равна и ниже) ее – у 52 объектов.
-
2.2.3. Оценка качества модели параллельных сечений
Оценку качества модели (9) выполним на основе данных о разности реальных значений цен и их оценок на основе тех же показателей, что и для регрессионной модели: коэффициента детерминации, ошибки модели оценки, средней ошибки аппроксимации, а также параметров распределения остатков модели.
Оценка коэффициента детерминации
На основе данных таблицы 18 рассчитаем значение коэффициента детерминации:
n 2 n 2
Z ( ? i - ? i) = 302110; £( ? - У ) = 2 528 676.
i =1 i =1
Отсюда R 2 = 1 -
2 528 676
= 0,88.
Рассчитаем значение скорректированного на количество степеней свободы (объем выборки и количество учитываемых влияющих факторов) коэффициента детерминации. В данном случае n = 108, m = 9 (2 зоны + 3 типа стен + 4 типа квартир):
R 2 = 1 - (1 - R 2)x
( n — 1)
( n - m -1)
1 - (1 - 0,88) x
108 -1
108 - 9 -1
0,87
Это означает, что модель оценки стоимости (9), реализованная по методу параллельных сечений, на 87 процентов объясняет изменение цен в экспериментальной выборке. Оставшиеся 13 процентов вариации цен выборки обусловлены факторами, не учитывае-
мыми моделью.
Оценка ошибки модели оценки
Ошибка модели оценки рассчитывается как выборочное среднеквадратичное отклонение по формуле (7). С учетом данных таблицы 18, а также с учетом того, что n = 108, m = 9, рассчитаем квадрат ошибки модели:
2 S îñò
n
Z ( У - - ?^ i )2
= i=1_____________ n - m -1
108 - 9 -1
3 083
Отсюда ошибка модели оценки S y = V2891 = 53,8 д. е.
S y 55,52
Относительная ошибка рассматриваемой модели 8 y = x 100% =----x 100% = 6,0% y 917
по величине незначительно отличается от аналогичного показателя (5,9 %) регрессионной модели.
Таблица 18
Рыночные цены и стоимости квартир, рассчитанные по методу параллельных сечений экспериментальной выборки
|
Н s |
<4 |
M <4 |
Дом |
Квартира |
=r |
i" Ф 5 |
$ 5 ф iS о 2 ° 1 о |
d s |
<4 |
M <4 |
Дом |
Квартира |
tn |
5 |
° 1 о |
||||||||||
|
’S § I |
>s 1 |
i Ф & 4 |
E 1 § |
E s 1 M |
E s 1 co |
E s 1 ^ |
'S § I |
>s 1 |
i ф & 4 |
1 § |
E s 1 M |
E s 1 co |
E s 1 ^ |
||||||||||||
|
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
800 |
784 |
0,98 |
55 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
840 |
840 |
1,00 |
|
2 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
802 |
784 |
0,98 |
56 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
860 |
840 |
0,98 |
|
3 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
750 |
784 |
1,05 |
57 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
960 |
943 |
0,98 |
|
4 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
760 |
784 |
1,03 |
58 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
962 |
943 |
0,98 |
|
5 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
798 |
784 |
0,98 |
59 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
912 |
943 |
1,03 |
|
6 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
804 |
784 |
0,98 |
60 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
958 |
943 |
0,98 |
|
7 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
880 |
862 |
0,98 |
61 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
966 |
943 |
0,98 |
|
8 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
805 |
862 |
1,07 |
62 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
850 |
1037 |
1,22 |
|
9 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
860 |
862 |
1,00 |
63 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1033 |
1037 |
1,00 |
|
10 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
880 |
862 |
0,98 |
64 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1050 |
1037 |
0,99 |
|
11 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
965 |
953 |
0,99 |
65 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1158 |
1147 |
0,99 |
|
12 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
989 |
953 |
0,96 |
66 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1166 |
1147 |
0,98 |
|
13 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
910 |
953 |
1,05 |
67 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1188 |
1147 |
0,97 |
|
14 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
990 |
953 |
0,96 |
68 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1122 |
1147 |
1,02 |
|
15 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
960 |
953 |
0,99 |
69 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1133 |
1147 |
1,01 |
|
16 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
969 |
953 |
0,98 |
70 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1280 |
1227 |
0,96 |
|
17 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1050 |
1020 |
0,97 |
71 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1270 |
1227 |
0,97 |
|
18 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1068 |
1020 |
0,96 |
72 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1260 |
1227 |
0,97 |
|
19 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1058 |
1020 |
0,96 |
73 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1200 |
1227 |
1,02 |
|
20 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1050 |
1020 |
0,97 |
74 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1260 |
1227 |
0,97 |
|
21 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
713 |
728 |
1,02 |
75 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
870 |
876 |
1,01 |
|
22 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
715 |
728 |
1,02 |
76 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
840 |
876 |
1,04 |
|
23 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
727 |
728 |
1,00 |
77 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
850 |
876 |
1,03 |
|
24 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
740 |
728 |
0,98 |
78 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
880 |
876 |
1,00 |
|
25 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
780 |
801 |
1,03 |
79 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
970 |
963 |
0,99 |
|
26 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
810 |
801 |
0,99 |
80 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
960 |
963 |
1,00 |
|
27 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
788 |
801 |
1,02 |
81 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
930 |
963 |
1,04 |
|
28 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
880 |
886 |
1,01 |
82 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
955 |
963 |
1,01 |
|
29 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
870 |
886 |
1,02 |
83 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1020 |
1066 |
1,05 |
|
30 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
850 |
886 |
1,04 |
84 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1044 |
1066 |
1,02 |
|
31 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
900 |
886 |
0,98 |
85 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1025 |
1066 |
1,04 |
|
32 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
860 |
886 |
1,03 |
86 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1045 |
1066 |
1,02 |
|
33 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
905 |
948 |
1,05 |
87 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1000 |
1066 |
1,07 |
|
34 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
945 |
948 |
1,00 |
88 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1144 |
1140 |
1,00 |
|
35 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1000 |
948 |
0,95 |
89 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1177 |
1140 |
0,97 |
|
36 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
920 |
948 |
1,03 |
90 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1188 |
1140 |
0,96 |
|
37 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
940 |
948 |
1,01 |
91 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1057 |
1140 |
1,08 |
|
38 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
635 |
645 |
1,02 |
92 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1111 |
1140 |
1,03 |
|
39 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
600 |
645 |
1,08 |
93 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
777 |
776 |
1,00 |
|
40 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
640 |
645 |
1,01 |
94 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
780 |
776 |
0,99 |
|
41 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
620 |
645 |
1,04 |
95 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1000 |
776 |
0,78 |
|
42 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
650 |
645 |
0,99 |
96 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
850 |
854 |
1,00 |
|
43 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
642 |
645 |
1,00 |
97 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
860 |
854 |
0,99 |
|
44 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
900 |
710 |
0,79 |
98 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
866 |
854 |
0,99 |
|
45 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
740 |
710 |
0,96 |
99 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
840 |
854 |
1,02 |
|
46 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
700 |
710 |
1,01 |
100 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
830 |
854 |
1,03 |
|
47 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
789 |
785 |
0,99 |
101 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
900 |
944 |
1,05 |
|
48 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
780 |
785 |
1,01 |
102 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1160 |
944 |
0,81 |
|
49 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
760 |
785 |
1,03 |
103 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
930 |
944 |
1,02 |
|
50 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
830 |
785 |
0,95 |
104 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
940 |
944 |
1,00 |
|
51 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
750 |
785 |
1,05 |
105 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1050 |
1010 |
0,96 |
|
52 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
810 |
840 |
1,04 |
106 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
800 |
1010 |
1,26 |
|
53 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
840 |
840 |
1,00 |
107 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
900 |
1010 |
1,12 |
|
54 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
870 |
840 |
0,97 |
108 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1000 |
1010 |
1,01 |
Если ошибки модели подчиняются нормальному закону распределения, можно с 95-процентной вероятностью утверждать, что ошибка оценки стоимости по модели не превышает ± t n х 55,5 = ±2 х 55,5 = ±111 д. е. (±12 процентов от среднего значения цены 917 д. е.), где tn – коэффициент Стьюдента, учитывающий конечный объем выборки, для рассматриваемых условий примерно равный 24. В других случаях расчет ширины доверительного интервала требует знания конкретного закона распределения ошибок.
Оценка средней ошибки аппроксимации
Средняя ошибка аппроксимации отражает свойства модели по воспроизведению исходных рыночных данных и рассчитывается по формуле (8). Рассчитанное на основе данных таблицы 18 значение средней ошибки аппроксимации модели, реализующей метод параллельных сечений, равно 3,4 процента, что практически не отличается от аналогичного показателя регрессионной модели и, как следует из таблицы 12, соответствует высокой точности модели оценки.
Анализ распределения остатков модели
На основе данных таблицы 18 с помощью Мастера диаграмм ППП MS Excel построим гистограмму частот отношений «оценка/цена» в исходных (рис. 3) и в стандартизованных (рис. 4) координатах.
|
Карман |
Частота |
|
0,78 |
1 |
|
0,82 |
2 |
|
0,87 |
0 |
|
0,92 |
0 |
|
0,97 |
14 |
|
1,02 |
58 |
|
1,07 |
27 |
|
1,12 |
3 |
|
1,17 |
1 |
|
1,21 |
0 |
|
Еще* |
2 |
|
Всего |
108 |
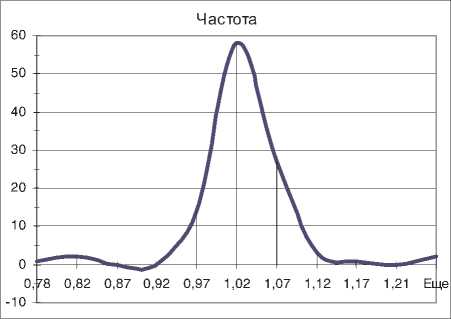
Рис. 3. Гистограмма частот отношений «оценка/цена» модели параллельных сечений
|
Карман |
Частота |
|
-3,75 |
1 |
|
-2,94 |
2 |
|
-2,14 |
0 |
|
-1,34 |
0 |
|
-0,53 |
14 |
|
0,27 |
58 |
|
1,07 |
27 |
|
1,88 |
3 |
|
2,68 |
1 |
|
3,48 |
0 |
|
Еще |
2 |
|
Всего |
108 |
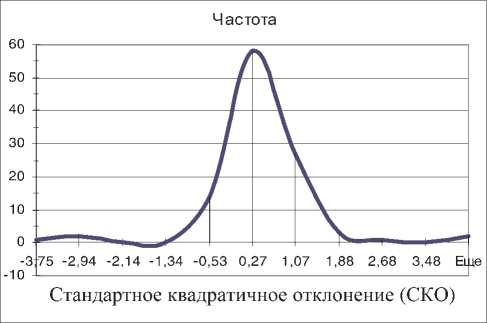
Рис. 4. Стандартизованная гистограмма частот отношений «оценка/цена» модели параллельных сечений
-
4 Точное значение t-статистики можно определить по справочной таблице критических значений t -статистики (критерии Стьюдента) или с помощью встроенной функции СТЬЮДРАСПОБР ( вероятность = 0,05, степени свободы = объем выборки минус число независимых переменных и минус единица). Здесь tn (0,05,98) = 1,9845.
-
2.2.4. Определение величины налогового коэффициента (Kн)
Из рисунков видно, что, как и в случае регрессионной модели, распределение частот отношений «оценка/цена» является одномодальным и имеет близкие к симметричным затухающие «крылья». Величина моды5 практически не отличается от среднего по выборке отношения (1,00). Это свидетельствует о том, что оцениваемые при помощи рассматриваемой модели средние значения цен хорошо соответствуют наиболее вероятным значениям, то есть рыночным стоимостям объектов.
Расчет налогового коэффициента проведем по алгоритму, описанному в пункте 2.1.6 для регрессионной модели.
Анализ данных расчета стоимости оцениваемых объектов (см. табл. 18) показывает, что в выборке имеется 13 квартир, отношение «оценка/цена» которых позволяет отнести их к категории объектов, имеющих существенное превышение стоимостей над ценами (значения стоимости превышают соответствующие значения цен в 1,05 и более раз). Максимальное значение коэффициента превышения составляет 1,26 (объект № 106), предыдущие по величине значения коэффициента превышения – 1,22 (объект № 62), 1,12 (объект № 107) и 1,08 (объекты № 39 и № 91).
При общем объеме выборки, равном 108 объектам, фактический уровень существенных превышений составляет: 13/108 = 12 процентов, поэтому для выполнения рекомендаций по заданному р-процентному уровню существенных превышений 1–3 процента необходимо применить понижающий налоговый коэффициент6.
Как и для регрессионной модели, установим 2-процентный уровень превышения. Для выборки из 108 объектов это означает, что после умножения на налоговый коэффициент модельных значений стоимостей в числе существенных превышений должны остаться два объекта (объекты № 106 и № 62) с максимальными значениями отношения «оцен-ка/цена», равными 1,26 и 1,22 соответственно. Расчет налогового коэффициента необходимо выполнять, ориентируясь на следующий за этими двумя объектами объект № 107, имеющий отношение «оценка/цена» 1,12.
Значение налогового коэффициента ( Кн2% ), как и ранее, найдем из следующего уравнения:
1,12 х Кн2 % = 1.
Отсюда Кн2% = 1/1,12 = 0,89 0,9.
С учетом налогового коэффициента минимальное значение отношения «оценка/цена» в группе превышения должно быть не менее 1,05. Для объекта № 62 условие 1,22 х Кн2 % = = 1,22 х 0,9 = 1,098 выполняется, следовательно, оно выполняется и для объекта № W6. Таким образом, заданный 2-процентный уровень превышения обеспечивается.
Информация о рыночных ценах на квартиры и соответствующих им налоговых стоимостях, полученных путем умножения расчетных значений рыночной стоимости на налоговый коэффициент 0,9, представлена в таблице 19. В этой же таблице приведены значения отношений налоговой стоимости и рыночной цены каждого объекта.
Как и ожидалось, в выборке рыночных цен и соответствующих им смоделированных значений налоговой стоимости имеется два объекта со значениями отношения «налоговая стоимость/цена», превышающими пороговое значение 1,05 (объекты № 106 – 1,14 и № 62 – 1,10). Еще один объект – № 107 имеет значение отношения 1,01. Значения стоимости для налогообложения остальных объектов лежат ниже соответствующих им рыночных цен. Среднее по всей выборке значение отношения «налоговая стоимость/цена» составляет 0,90, минимальное – 0,70.
Значение налогового коэффициента, рассчитанное в предположении о нормальности распределения ошибок модели, составляет:
Кн2д = 1 — 1,96 х 0,06 = 0,88.
Таблица 19
Рыночные цены и налоговые стоимости квартир, рассчитанные по методу параллельных сечений экспериментальной выборки
|
Ц s |
s <4 |
M s <4 |
Дом |
Квартира |
5ч 3 =r |
S £ 2 | X и |
° I u |
d s |
<4 |
M s <4 |
Дом |
Квартира |
S4 3 |
S iS Q о X о |
° 2 u |
||||||||||
|
’S ■0 t |
’S 1 |
’S Ф & 4 |
E s 1 |
Ф M |
co |
^ |
'S ■0 I |
'S 1 1 |
'S ф & 4 |
s 1 |
£ M |
£ co |
^ |
||||||||||||
|
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
800 |
705 |
0,88 |
55 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
840 |
756 |
0,90 |
|
2 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
802 |
705 |
0,88 |
56 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
860 |
756 |
0,88 |
|
3 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
750 |
705 |
0,94 |
57 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
960 |
849 |
0,88 |
|
4 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
760 |
705 |
0,93 |
58 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
962 |
849 |
0,88 |
|
5 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
798 |
705 |
0,88 |
59 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
912 |
849 |
0,93 |
|
6 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
804 |
705 |
0,88 |
60 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
958 |
849 |
0,89 |
|
7 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
880 |
776 |
0,88 |
61 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
966 |
849 |
0,88 |
|
8 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
805 |
776 |
0,96 |
62 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
850 |
933 |
1,10 |
|
9 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
860 |
776 |
0,90 |
63 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1033 |
933 |
0,90 |
|
10 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
880 |
776 |
0,88 |
64 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1050 |
933 |
0,89 |
|
11 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
965 |
858 |
0,89 |
65 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1158 |
1032 |
0,89 |
|
12 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
989 |
858 |
0,87 |
66 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1166 |
1032 |
0,89 |
|
13 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
910 |
858 |
0,94 |
67 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1188 |
1032 |
0,87 |
|
14 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
990 |
858 |
0,87 |
68 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1122 |
1032 |
0,92 |
|
15 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
960 |
858 |
0,89 |
69 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1133 |
1032 |
0,91 |
|
16 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
969 |
858 |
0,89 |
70 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1280 |
1104 |
0,86 |
|
17 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1050 |
918 |
0,87 |
71 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1270 |
1104 |
0,87 |
|
18 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1068 |
918 |
0,86 |
72 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1260 |
1104 |
0,88 |
|
19 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1058 |
918 |
0,87 |
73 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1200 |
1104 |
0,92 |
|
20 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1050 |
918 |
0,87 |
74 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1260 |
1104 |
0,88 |
|
21 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
713 |
655 |
0,92 |
75 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
870 |
788 |
0,91 |
|
22 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
715 |
655 |
0,92 |
76 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
840 |
788 |
0,94 |
|
23 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
727 |
655 |
0,90 |
77 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
850 |
788 |
0,93 |
|
24 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
740 |
655 |
0,89 |
78 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
880 |
788 |
0,90 |
|
25 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
780 |
721 |
0,92 |
79 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
970 |
867 |
0,89 |
|
26 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
810 |
721 |
0,89 |
80 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
960 |
867 |
0,90 |
|
27 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
788 |
721 |
0,91 |
81 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
930 |
867 |
0,93 |
|
28 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
880 |
797 |
0,91 |
82 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
955 |
867 |
0,91 |
|
29 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
870 |
797 |
0,92 |
83 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1020 |
959 |
0,94 |
|
30 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
850 |
797 |
0,94 |
84 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1044 |
959 |
0,92 |
|
31 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
900 |
797 |
0,89 |
85 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1025 |
959 |
0,94 |
|
32 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
860 |
797 |
0,93 |
86 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1045 |
959 |
0,92 |
|
33 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
905 |
853 |
0,94 |
87 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1000 |
959 |
0,96 |
|
34 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
945 |
853 |
0,90 |
88 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1144 |
1026 |
0,90 |
|
35 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1000 |
853 |
0,85 |
89 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1177 |
1026 |
0,87 |
|
36 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
920 |
853 |
0,93 |
90 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1188 |
1026 |
0,86 |
|
37 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
940 |
853 |
0,91 |
91 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1057 |
1026 |
0,97 |
|
38 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
635 |
581 |
0,91 |
92 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1111 |
1026 |
0,92 |
|
39 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
600 |
581 |
0,97 |
93 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
777 |
699 |
0,90 |
|
40 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
640 |
581 |
0,91 |
94 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
780 |
699 |
0,90 |
|
41 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
620 |
581 |
0,94 |
95 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1000 |
699 |
0,70 |
|
42 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
650 |
581 |
0,89 |
96 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
850 |
768 |
0,90 |
|
43 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
642 |
581 |
0,90 |
97 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
860 |
768 |
0,89 |
|
44 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
900 |
639 |
0,71 |
98 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
866 |
768 |
0,89 |
|
45 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
740 |
639 |
0,86 |
99 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
840 |
768 |
0,91 |
|
46 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
700 |
639 |
0,91 |
100 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
830 |
768 |
0,93 |
|
47 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
789 |
707 |
0,90 |
101 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
900 |
850 |
0,94 |
|
48 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
780 |
707 |
0,91 |
102 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1160 |
850 |
0,73 |
|
49 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
760 |
707 |
0,93 |
103 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
930 |
850 |
0,91 |
|
50 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
830 |
707 |
0,85 |
104 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
940 |
850 |
0,90 |
|
51 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
750 |
707 |
0,94 |
105 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1050 |
909 |
0,87 |
|
52 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
810 |
756 |
0,93 |
106 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
800 |
909 |
1,14 |
|
53 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
840 |
756 |
0,90 |
107 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
900 |
909 |
1,01 |
|
54 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
870 |
756 |
0,87 |
108 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1000 |
909 |
0,91 |
Расчеты показывают, что при применении значения налогового коэффициента Кн2% = 0,88 в выборке также остаются 2 объекта, для которых отношение «налоговая стои-мость/цена» превышает пороговое значение (объекты № 106 и № 62). Налоговые стоимости остальных объектов ниже рыночных. Среднее по всей выборке значение отношения «налоговая стоимость/цена» составляет 0,883, минимальное – 0,68.
-
2.2.5. Порядок определения базовых ставок и коэффициентов модели
-
2.3. Кластерная модель, основанная на методе последовательных сечений
-
2.3.1. Расчет коэффициентов модели, основанной на методе последовательных сечений Расчет базовой ставки стоимости
Базовые ставки и коэффициенты модели, реализующей метод параллельных сечений экспериментальной выборки, определяются в соответствие с данными, полученными в пункте 2.2.1.
Модель оценки стоимости, основанная на методе последовательных сечений, может быть реализована в рамках той же формулы, что и две предыдущие модели:
j? = Na x E x K 2 x E 3 . (9)
В методе последовательных сечений, как и в методе параллельных сечений, в качестве базовой ставки стоимости ( СБ ) берется средняя по всей экспериментальной выборке цена 1 квадратного метра общей площади объектов недвижимости:
y = СБ = 917 д. е.
Расчет коэффициента местоположения
Значение коэффициента местоположения зависит от ценовой зоны. Учитывая, что фактор местоположения является одним из самых существенных для объекта недвижимости, как правило, именно по местоположению проводится первая дифференциация экспериментальной выборки на однородные группы. В методе последовательных сечений, как и в методе параллельных сечений, значение коэффициента местоположения (ценовой зоны) рассчитывается как отношение средней цены 1 квадратного метра общей площади объектов недвижимости, находящихся в данной ценовой зоне, к средней по всей экспериментальной выборке цене 1 квадратного метра общей площади объектов.
Используя данные таблицы 2 или 3, определим средние значения удельных цен объектов недвижимости ценовых зон: среднее значение цен 1-й зоны равно 835 д. е, 2-й зоны – 1 005 д. е. Эти данные позволяют рассчитать значения коэффициента местоположения (табл. 20).
Расчет коэффициента местоположения (K1)
Таблица 20
|
Номер ценовой зоны |
Значение K1 |
|
1 |
K11 = 835/917 = 0,911 |
|
2 |
K12 = 1005/917 = 1,096 |
Расчет коэффициента материала стен ( K2 )
Для расчета значений коэффициента материала стен по данным таблицы 2 или 3 необходимо предварительно рассчитать средние значения удельных цен объектов недвижимости, имеющих разные материалы стен.
В соответствии с процедурой построения модели оценки стоимости, основанной на методе последовательных сечений, это нужно сделать отдельно по зонам.
Для 1-й ценовой зоны:
-
• среднее значение цен объектов с кирпичными стенами = 907 д. е.;
-
• среднее значение цен объектов с блочными стенами = 844 д. е.;
-
• среднее значение цен объектов с деревянными стенами = 750 д. е.
Для 2-й ценовой зоны:
-
• среднее значение цен объектов с кирпичными стенами = 1096 д. е.;
-
• среднее значение цен объектов с блочными стенами = 1004 д. е.;
-
• среднее значение цен объектов с деревянными стенами = 905 д. е.
Для расчета значений коэффициентов материала стен (K2) необходимо поделить средние значения удельных цен объектов недвижимости, имеющих разный материал стен, на средние значения цен всех объектов недвижимости, находящихся в соответствующих зонах. Иными словами, необходимо предварительно разбить каждую полученную на первом шаге сечений зону на группы, содержащие только объекты с интересующим материалом стен (табл. 21).
Таблица 21
Расчет коэффициента материала стен (K2)
|
Номер ценовой зоны |
Стены |
Значение K2 |
|
1 |
кирпичные |
K21 = 907/835 = 1,086 |
|
1 |
блочные |
K 2 2 = 844/835 = 1,011 |
|
1 |
деревянные |
K23 = 750/835 = 0,898 |
|
2 |
кирпичные |
K24 = 1096/1005 = 1,091 |
|
2 |
блочные |
K25 = 1004/1005 = 0,999 |
|
2 |
деревянные |
K26 = 905/1005 = 0,900 |
Расчет коэффициента количества комнат ( K3 )
В модели, основанной на методе последовательных сечений, для расчета значений коэффициента количества комнат на основе данных таблиц 2 или 3 необходимо предварительно рассчитать средние значения удельных цен объектов недвижимости, имеющих разное количество комнат. Это нужно сделать отдельно по ценовым зонам и материалам стен (табл. 22)7.
Таблица 22
Расчет средних значений цен квартир в зависимости от количества комнат
|
Ценовая зона |
Стены |
Количество комнат |
Среднее значение цены, д. е. |
|
1 |
кирпичные |
1 |
786 |
|
1 |
кирпичные |
2 |
856 |
|
1 |
кирпичные |
3 |
964 |
|
1 |
кирпичные |
4 |
1 057 |
|
1 |
блочные |
1 |
724 |
|
1 |
блочные |
2 |
793 |
|
1 |
блочные |
3 |
872 |
|
1 |
блочные |
4 |
942 |
|
1 |
деревянные |
1 |
631 |
|
1 |
деревянные |
2 |
780 |
|
1 |
деревянные |
3 |
782 |
|
1 |
деревянные |
4 |
844 |
|
2 |
кирпичные |
1 |
952 |
|
2 |
кирпичные |
2 |
978 |
|
2 |
кирпичные |
3 |
1153 |
|
2 |
кирпичные |
4 |
1 254 |
|
2 |
блочные |
1 |
860 |
|
2 |
блочные |
2 |
954 |
|
2 |
блочные |
3 |
1 027 |
|
2 |
блочные |
4 |
1 135 |
|
2 |
деревянные |
1 |
852 |
|
2 |
деревянные |
2 |
849 |
|
2 |
деревянные |
3 |
983 |
|
2 |
деревянные |
4 |
938 |
7 Средние значения цен, представленные в таблице 22, можно использовать для налогообложения в качестве справочника цен по группам квартир, имеющих общие признаки.
Для расчета значений коэффициента количества комнат (K3) необходимо поделить средние значения удельных цен объектов недвижимости, имеющих разное количество комнат, на средние значения цен объектов недвижимости, имеющих разные материалы стен. Причем сделать это надо отдельно по ценовым зонам (табл. 23).
Таблица 23
Расчет коэффициента количества комнат (K3)
|
Ценовая зона |
Стены |
Количество комнат |
Значение K3 |
|
1 |
кирпичные |
1 |
K31 = 786/907 = 0,867 |
|
1 |
кирпичные |
2 |
K32 = 856/907 = 0,944 |
|
1 |
кирпичные |
3 |
K33 = 964/907 = 1,063 |
|
1 |
кирпичные |
4 |
K34 = 1057/907 = 1,165 |
|
1 |
блочные |
1 |
K35 = 724/844 = 0,858 |
|
1 |
блочные |
2 |
K36 = 793/844 = 0,940 |
|
1 |
блочные |
3 |
K37 = 872/844 = 1,033 |
|
1 |
блочные |
4 |
K38 = 942/844 = 1,116 |
|
1 |
деревянные |
1 |
K39 = 631/750 = 0,841 |
|
1 |
деревянные |
2 |
K310 = 780/750 = 1,040 |
|
1 |
деревянные |
3 |
K311 = 782/750 = 1,043 |
|
1 |
деревянные |
4 |
K312 = 844/750 = 1,125 |
|
2 |
кирпичные |
1 |
K313 = 952/1096 = 0,869 |
|
2 |
кирпичные |
2 |
K314 = 978/1096 = 0,892 |
|
2 |
кирпичные |
3 |
K315 = 1153/1096 = 1,052 |
|
2 |
кирпичные |
4 |
K316 = 1254/1096 = 1,144 |
|
2 |
блочные |
1 |
K317 = 860/1004 = 0,857 |
|
2 |
блочные |
2 |
K318 = 954/1004 = 0,950 |
|
2 |
блочные |
3 |
K319 = 1027/1004 = 1,023 |
|
2 |
блочные |
4 |
K320 = 1135/1004 = 1,130 |
|
2 |
деревянные |
1 |
K321 = 852/905 = 0,941 |
|
2 |
деревянные |
2 |
K322 = 849/905 = 0,938 |
|
2 |
деревянные |
3 |
K323 = 983/905 = 1,086 |
|
2 |
деревянные |
4 |
K324 = 938/905 = 1,036 |
-
2.3.2. Расчет значений стоимости квартир с помощью модели последовательных сечений
Расчетные значения стоимости единицы общей площади оцениваемых квартир могут быть получены по формуле (9) с использованием коэффициентов, представленных в таблицах 20, 21 и 23 (см. п. 2.3.1)8.
Так, например, для объекта № 1 (зона 1, кирпичный, однокомнатная):
/ i = Na x E 1 x K 2 x E 3 = 917 x 0,911 x 1,086 x 0,867 = 787 д. е.
Для объекта № 55 (зона 1, деревянный, 4-комнатная):
/ 55 = N x E 1 x K 3 x E 32 = 917 x 0,911 x 0,898 x 1,125 = 844 д. е.
Для объекта № 87 (зона 2, блочный, 3-комнатная):
/ 87 = Na x E 2 x K 5 x E 39 = 917 x 1,096 x 0,999 x 1,023 = 1027 д. е.
Результаты расчета рыночных стоимостей оцениваемых квартир представлены в таблице 24.
Таблица 24
|
ll s |
<4 |
M <4 |
Дом |
Квартира |
3 =r |
i" 5 |
1 ° 8 и |
11 s |
<4 |
M <4 |
Дом |
Квартира |
3 |
i 5 |
1 ° s и |
||||||||||
|
>s i 1 |
’S ■0 0 6 |
I & 4 |
s 1 |
1 M |
1 co |
I ^ |
>s 1 |
'S ■0 0 6 |
^ i Ф & 4 |
s 1 |
£ 1 M |
£ 1 co |
I ^ |
||||||||||||
|
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
800 |
787 |
0,98 |
55 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
840 |
844 |
1,00 |
|
2 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
802 |
787 |
0,98 |
56 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
860 |
844 |
0,98 |
|
3 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
750 |
787 |
1,05 |
57 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
960 |
953 |
0,99 |
|
4 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
760 |
787 |
1,04 |
58 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
962 |
953 |
0,99 |
|
5 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
798 |
787 |
0,99 |
59 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
912 |
953 |
1,04 |
|
6 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
804 |
787 |
0,98 |
60 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
958 |
953 |
0,99 |
|
7 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
880 |
856 |
0,97 |
61 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
966 |
953 |
0,99 |
|
8 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
805 |
856 |
1,06 |
62 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
850 |
978 |
1,15 |
|
9 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
860 |
856 |
0,99 |
63 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1033 |
978 |
0,95 |
|
10 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
880 |
856 |
0,97 |
64 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1050 |
978 |
0,93 |
|
11 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
965 |
964 |
1,00 |
65 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1158 |
1154 |
1,00 |
|
12 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
989 |
964 |
0,97 |
66 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1166 |
1154 |
0,99 |
|
13 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
910 |
964 |
1,06 |
67 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1188 |
1154 |
0,97 |
|
14 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
990 |
964 |
0,97 |
68 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1122 |
1154 |
1,03 |
|
15 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
960 |
964 |
1,00 |
69 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1133 |
1154 |
1,02 |
|
16 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
969 |
964 |
0,99 |
70 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1280 |
1254 |
0,98 |
|
17 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1050 |
1057 |
1,01 |
71 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1270 |
1254 |
0,98 |
|
18 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1068 |
1057 |
0,99 |
72 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1260 |
1254 |
0,99 |
|
19 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1058 |
1057 |
1,00 |
73 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1200 |
1254 |
1,05 |
|
20 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1050 |
1057 |
1,01 |
74 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1260 |
1254 |
0,99 |
|
21 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
713 |
725 |
1,02 |
75 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
870 |
860 |
0,99 |
|
22 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
715 |
725 |
1,01 |
76 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
840 |
860 |
1,02 |
|
23 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
727 |
725 |
1,00 |
77 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
850 |
860 |
1,01 |
|
24 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
740 |
725 |
0,98 |
78 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
880 |
860 |
0,98 |
|
25 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
780 |
794 |
1,02 |
79 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
970 |
954 |
0,98 |
|
26 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
810 |
794 |
0,98 |
80 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
960 |
954 |
0,99 |
|
27 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
788 |
794 |
1,01 |
81 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
930 |
954 |
1,03 |
|
28 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
880 |
872 |
0,99 |
82 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
955 |
954 |
1,00 |
|
29 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
870 |
872 |
1,00 |
83 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1020 |
1027 |
1,01 |
|
30 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
850 |
872 |
1,03 |
84 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1044 |
1027 |
0,98 |
|
31 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
900 |
872 |
0,97 |
85 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1025 |
1027 |
1,00 |
|
32 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
860 |
872 |
1,01 |
86 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1045 |
1027 |
0,98 |
|
33 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
905 |
943 |
1,04 |
87 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1000 |
1027 |
1,03 |
|
34 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
945 |
943 |
1,00 |
88 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1144 |
1135 |
0,99 |
|
35 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1000 |
943 |
0,94 |
89 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1177 |
1135 |
0,96 |
|
36 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
920 |
943 |
1,03 |
90 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1188 |
1135 |
0,96 |
|
37 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
940 |
943 |
1,00 |
91 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1057 |
1135 |
0,98 |
|
38 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
635 |
631 |
0,99 |
92 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1111 |
1135 |
1,02 |
|
39 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
600 |
631 |
1,05 |
93 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
777 |
851 |
1,10 |
|
40 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
640 |
631 |
0,99 |
94 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
780 |
851 |
1,09 |
|
41 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
620 |
631 |
1,02 |
95 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1000 |
851 |
0,85 |
|
42 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
650 |
631 |
0,97 |
96 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
850 |
848 |
1,00 |
|
43 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
642 |
631 |
0,98 |
97 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
860 |
848 |
0,99 |
|
44 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
900 |
780 |
0,87 |
98 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
866 |
848 |
0,98 |
|
45 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
740 |
780 |
1,05 |
99 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
840 |
848 |
1,01 |
|
46 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
700 |
780 |
1,11 |
100 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
830 |
848 |
1,02 |
|
47 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
789 |
782 |
0,99 |
101 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
900 |
982 |
1,09 |
|
48 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
780 |
782 |
1,00 |
102 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1160 |
982 |
0,85 |
|
49 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
760 |
782 |
1,03 |
103 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
930 |
982 |
1,06 |
|
50 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
830 |
782 |
0,94 |
104 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
940 |
982 |
1,04 |
|
51 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
750 |
782 |
1,04 |
105 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1050 |
937 |
0,89 |
|
52 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
810 |
844 |
1,04 |
106 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
800 |
937 |
1,17 |
|
53 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
840 |
844 |
1,00 |
107 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
900 |
937 |
1,04 |
|
54 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
870 |
844 |
0,97 |
108 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1000 |
937 |
0,94 |
Анализ результатов расчета показывает, что среднее по всей выборке значение отношения «оценка/цена» составляет 1,00, минимальное – 0,847 (объект № 95), максимальное – 1,17 (объект № 106). Из 108 объектов выборки оценка превышает цену у 47 объектов и находится ниже ее – у 61 объекта.
-
2.3.3. Оценка качества модели оценки, основанной на методе последовательных сечений
Оценка коэффициента детерминации
Коэффициент детерминации рассчитывается с использованием данных таблицы 24 по формуле (6) (см. п. 2.1.5):
n n 2
E ( y , - y , ) = 210 079 ; £( y , - y ) = 2 528 676 .
i =1 i =1
Отсюда R 2 = 1 -
210 079
2528 676
= 0,92.
Рыночные цены и стоимости квартир, рассчитанные методом последовательных сечений экспериментальной выборки
Скорректированный на число степеней свободы коэффициент детерминации с учетом того, что m = 24 (количество однородных групп на последнем шаге сечений), равен:
108 -1
108 - 24 -1
= 0,90.
/R 2 = 1 - (1 - R 2) x ( n 1) = 1 - (1 - 0,92) x
( n - m -1)
Это означает, что модель оценки стоимости, основанная на методе последовательных сечений, объясняет вариацию цен в экспериментальной выборке на 90 процентов, остальные 10 процентов изменений обусловлены влиянием неучтенных моделью факторов.
Оценка ошибки модели оценки
Как уже отмечалось, точность получаемых моделью значений оценок в рамках анализируемого подхода определяется точностью результата последнего шага сечений. Именно по данным о ценах объектов, отнесенных к каждой группе этого сечения, определяется среднее значений цены, совпадающее с соответствующим значением модельной оценки. Поэтому ошибки модели оценки, основанной на методе последовательных сечений, рассчитаем как среднеквадратичную ошибку оценки среднего значения для каждой j -й группы последнего сечения по формуле (10), в которую преобразовывается выражение (7), учитывая, что m = 0, n = nj – числу объектов, отнесенных к данной группе:
nj
E ( y , - / )2
sj - , ; s , 2 = i' „ . . (10)
nj-1
Результаты расчета ошибок модели, основанной на методе последовательных сечений, выполненных с использованием данных таблиц 3 и 23, сведены в таблицу 25.
Среднее по всем группам значение среднеквадратичной ошибки оценки составляет
Sy = 42,9 д. е. Значения относительной ошибки, определяемые для каждой группы объ- yj лежат в пределах 1–15 процентов при среднем
ектов последнего сечения как 8y, = значении 8y = 4,7 %. Отметим, что максимальные значения относительных ошибок (11-15 %), как и следовало ожидать, соответствуют группам с минимальным числом (3–4) наблюдений в группе.
Оценка средней ошибки аппроксимации
Средняя ошибка аппроксимации модели последовательных сечений, рассчитанная по формуле (8) и данным таблицы 24, равна 3,0 процента, что соответствует высокой точности модели оценки (см. табл. 12).
Анализ распределения остатков модели
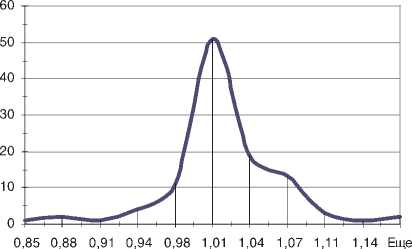
Построенные на основе данных таблицы 24 гистограммы частот отношений «оценка/це-на» модели последовательных сечений в исходных и стандартизованных координатах представлены на рисунках 5 и 6.
Таблица 25
Показатели точности расчета стоимости методом последовательных сечений
|
Карман |
Частота |
|
0,85 |
1 |
|
0,88 |
2 |
|
0,91 |
1 |
|
0,94 |
4 |
|
0,98 |
11 |
|
1,01 |
51 |
|
1,04 |
19 |
|
1,07 |
13 |
|
1,11 |
3 |
|
1,14 |
1 |
|
Еще |
2 |
|
Всего |
108 |
Частота
|
Ценовая зона |
Стены |
Количество комнат |
Среднее значение цены, д. е. |
Число объектов в группе |
Ошибка модели Sj, д. е. |
Относительная ошибка, % |
|
1 |
кирпичные |
1 |
786 |
6 |
24 |
3 |
|
1 |
кирпичные |
2 |
856 |
4 |
35 |
4 |
|
1 |
кирпичные |
3 |
964 |
6 |
29 |
3 |
|
1 |
кирпичные |
4 |
1057 |
4 |
9 |
1 |
|
1 |
блочные |
1 |
724 |
4 |
13 |
2 |
|
1 |
блочные |
2 |
793 |
3 |
16 |
2 |
|
1 |
блочные |
3 |
872 |
5 |
19 |
2 |
|
1 |
блочные |
4 |
942 |
5 |
36 |
4 |
|
1 |
деревянные |
1 |
631 |
6 |
18 |
3 |
|
1 |
деревянные |
2 |
780 |
3 |
106 |
14 |
|
1 |
деревянные |
3 |
782 |
5 |
31 |
4 |
|
1 |
деревянные |
4 |
844 |
5 |
23 |
3 |
|
2 |
кирпичные |
1 |
952 |
5 |
22 |
2 |
|
2 |
кирпичные |
2 |
978 |
3 |
111 |
11 |
|
2 |
кирпичные |
3 |
1153 |
5 |
26 |
2 |
|
2 |
кирпичные |
4 |
1254 |
5 |
31 |
2 |
|
2 |
блочные |
1 |
860 |
4 |
18 |
2 |
|
2 |
блочные |
2 |
954 |
4 |
18 |
2 |
|
2 |
блочные |
3 |
1027 |
5 |
19 |
2 |
|
2 |
блочные |
4 |
1135 |
5 |
53 |
5 |
|
2 |
деревянные |
1 |
852 |
3 |
128 |
15 |
|
2 |
деревянные |
2 |
849 |
5 |
15 |
2 |
|
2 |
деревянные |
3 |
983 |
4 |
120 |
12 |
|
2 |
деревянные |
4 |
938 |
4 |
111 |
12 |
Рис. 5. Гистограмма частот отношений «оценка/цена» модели последовательных сечений
Карман Частота
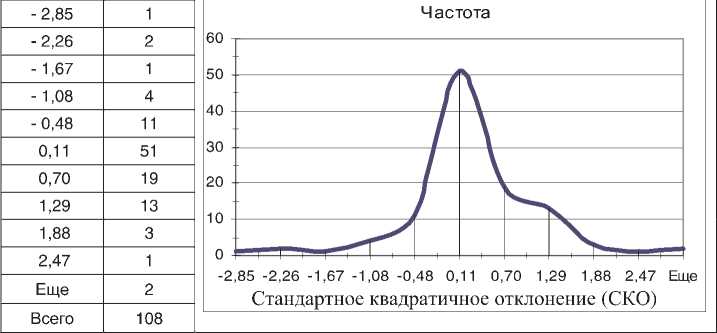
Рис. 6. Стандартизованная гистограмма частот отношений «оценка/цена» модели последовательных сечений
Из рисунков видно, что распределение частот отношений «оценка/цена» также является одномодальным, однако с явно выраженной асимметрией правого «крыла» распределения. Модальное значение9 составляет 1,00 и практически совпадает со средним по выборке значением отношения «оценка/цена». Это, как отмечалось, свидетельствует о том, что оцениваемые с использованием этой модели средние значения цен хорошо соответствуют наиболее вероятным значениям, то есть рыночным стоимостям объектов.
Здесь, как и в модели параллельных сечений, можно отметить наличие в выборке значений, отстоящих более чем на ±3 значения среднеквадратичного отклонения (СКО) от центра группирования (рис. 6). В таблице 24 к таким выделяющимся объектам можно отнести цены на квартиры с номерами наблюдений 62, 106, с одной стороны, и 95, 44 – с другой.
-
2.3.4. Определение величины налогового коэффициента (Kн)
Расчетные данные (см. табл. 24) показывают, что в выборке имеются 13 объектов, для которых значения стоимости превышают соответствующие значения цен в 1,05 и более раз, причем максимальное значение превышения составляет 1,17 (объект № 106), предыдущие по величине значения коэффициента превышения – 1,15 (объект № 62) и 1,11 (объект № 46).
При общем объеме выборки, равном 108 объектам, фактический уровень существенных превышений составляет 13/108 = 12 %. Для 2-процентного уровня превышения расчет налогового коэффициента необходимо выполнять, ориентируясь на объект № 46, имеющий третье по величине отношение «оценка/цена» – 1,11. Значение налогового коэффициента найдем, как и прежде, из соотношения:
1,11 X К н2% = 1.
Отсюда Кн2% = 0,90.
Проверим выполнение заданного уровня превышений. С учетом применения налогового коэффициента минимальное значение отношения «оценка/цена» в группе превышения должно быть не менее 1,05. Для объекта № 62 условие 1,15 х Кн2 % = 1,15 х 0,9 = 1,035 не выполняется , следовательно, необходимо повысить значение налогового коэффициента до уровня, обеспечивающего следующее равенство:
1,15 х Кн2 % = 1,05
где 1,05 – граница «существенности» превышения.
Отсюда значение налогового коэффициента должно равняться:
Кн2 % = 1,05/1,15 = 0,913 = 0,91.
При таком значении налогового коэффициента имеется два объекта с существенными превышениями оценок над ценами (№ 62 и № 106), остальные отношения не превышают порогового значения, то есть заданный 2-процентный уровень превышения обеспечивается.
Таблица 26
Рыночные цены и налоговые стоимости квартир, полученные методом последовательных сечений экспериментальной выборки
|
d $ i s |
СУ § co |
cm tn § co |
Дом |
Квартира |
s =r |
0; -0 co S 0 В I o |
СУ о о о |
d s |
су co |
<м су со |
Дом |
Квартира |
s |
В jO у о X о |
су о g о |
||||||||||
|
>s i 1 |
’S 1 |
’S i CD & 4 |
E s 1 |
CM |
co |
I ^ |
>s 1 |
'S 1 1 |
'S 1 CD & 4 |
E s 1 |
£ CM |
£ co |
I § ^ |
||||||||||||
|
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
800 |
716 |
0,90 |
55 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
840 |
768 |
0,91 |
|
2 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
802 |
716 |
0,89 |
56 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
860 |
768 |
0,89 |
|
3 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
750 |
716 |
0,95 |
57 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
960 |
867 |
0,90 |
|
4 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
760 |
716 |
0,94 |
58 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
962 |
867 |
0,90 |
|
5 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
798 |
716 |
0,90 |
59 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
912 |
867 |
0,95 |
|
6 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
804 |
716 |
0,89 |
60 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
958 |
867 |
0,91 |
|
7 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
880 |
779 |
0,89 |
61 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
966 |
867 |
0,90 |
|
8 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
805 |
779 |
0,97 |
62 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
850 |
890 |
1,05 |
|
9 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
860 |
779 |
0,91 |
63 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1033 |
890 |
0,86 |
|
10 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
880 |
779 |
0,89 |
64 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1050 |
890 |
0,85 |
|
11 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
965 |
877 |
0,91 |
65 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1158 |
1050 |
0,91 |
|
12 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
989 |
877 |
0,89 |
66 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1166 |
1050 |
0,90 |
|
13 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
910 |
877 |
0,96 |
67 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1188 |
1050 |
0,88 |
|
14 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
990 |
877 |
0,89 |
68 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1122 |
1050 |
0,94 |
|
15 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
960 |
877 |
0,91 |
69 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1133 |
1050 |
0,93 |
|
16 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
969 |
877 |
0,91 |
70 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1280 |
1141 |
0,89 |
|
17 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1050 |
962 |
0,92 |
71 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1270 |
1141 |
0,90 |
|
18 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1068 |
962 |
0,90 |
72 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1260 |
1141 |
0,91 |
|
19 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1058 |
962 |
0,91 |
73 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1200 |
1141 |
0,95 |
|
20 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1050 |
962 |
0,92 |
74 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1260 |
1141 |
0,91 |
|
21 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
713 |
660 |
0,93 |
75 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
870 |
783 |
0,90 |
|
22 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
715 |
660 |
0,92 |
76 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
840 |
783 |
0,93 |
|
23 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
727 |
660 |
0,91 |
77 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
850 |
783 |
0,92 |
|
24 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
740 |
660 |
0,89 |
78 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
880 |
783 |
0,89 |
|
25 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
780 |
723 |
0,93 |
79 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
970 |
868 |
0,89 |
|
26 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
810 |
723 |
0,89 |
80 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
960 |
868 |
0,90 |
|
27 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
788 |
723 |
0,92 |
81 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
930 |
868 |
0,93 |
|
28 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
880 |
794 |
0,90 |
82 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
955 |
868 |
0,91 |
|
29 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
870 |
794 |
0,91 |
83 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1020 |
935 |
0,92 |
|
30 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
850 |
794 |
0,93 |
84 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1044 |
935 |
0,90 |
|
31 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
900 |
794 |
0,88 |
85 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1025 |
935 |
0,91 |
|
32 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
860 |
794 |
0,92 |
86 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1045 |
935 |
0,89 |
|
33 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
905 |
858 |
0,95 |
87 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1000 |
935 |
0,94 |
|
34 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
945 |
858 |
0,91 |
88 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1144 |
1033 |
0,90 |
|
35 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1000 |
858 |
0,86 |
89 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1177 |
1033 |
0,88 |
|
36 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
920 |
858 |
0,93 |
90 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1188 |
1033 |
0,87 |
|
37 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
940 |
858 |
0,91 |
91 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1057 |
1033 |
0,98 |
|
38 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
635 |
574 |
0,90 |
92 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1111 |
1033 |
0,93 |
|
39 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
600 |
574 |
0,96 |
93 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
777 |
774 |
1,00 |
|
40 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
640 |
574 |
0,90 |
94 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
780 |
774 |
0,99 |
|
41 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
620 |
574 |
0,93 |
95 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1000 |
774 |
0,77 |
|
42 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
650 |
574 |
0,88 |
96 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
850 |
772 |
0,91 |
|
43 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
642 |
574 |
0,89 |
97 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
860 |
772 |
0,90 |
|
44 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
900 |
710 |
0,79 |
98 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
866 |
772 |
0,89 |
|
45 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
740 |
710 |
0,96 |
99 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
840 |
772 |
0,92 |
|
46 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
700 |
710 |
1,01 |
100 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
830 |
772 |
0,93 |
|
47 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
789 |
712 |
0,90 |
101 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
900 |
894 |
0,99 |
|
48 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
780 |
712 |
0,91 |
102 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1160 |
894 |
0,77 |
|
49 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
760 |
712 |
0,94 |
103 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
930 |
894 |
0,96 |
|
50 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
830 |
712 |
0,86 |
104 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
940 |
894 |
0,95 |
|
51 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
750 |
712 |
0,95 |
105 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1050 |
853 |
0,81 |
|
52 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
810 |
768 |
0,95 |
106 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
800 |
853 |
1,07 |
|
53 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
840 |
768 |
0,91 |
107 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
900 |
853 |
0,95 |
|
54 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
870 |
768 |
0,88 |
108 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1000 |
853 |
0,85 |
В предположении о нормальном законе распределения исходных данных значение налогового коэффициента, рассчитываемое на основе значения относительной ошибки модели (см. п. 2.3.3), можно определить следующим образом:
Кн2 5 = 1 — 1,96 х 0,047 = 0,91.
В данном случае рассчитанные на основе двух различных подходов значения налогового коэффициента практически совпадают.
В таблице 26 представлена информация о рыночных ценах на квартиры и соответствующих им налоговых стоимостях, полученных путем умножения расчетных значений стоимостей на принятое значение налогового коэффициента 0,91.
Как и ожидалось, в выборке рыночных цен и соответствующих им смоделированных значений налоговой стоимости имеются два объекта с отношением «налоговая стои-мость/цена», достигающим пороговое значение 1,05 (объект № 62) и превышающим это значение (объект № 106 – 1,07). Также имеется один объект (№ 46) с отношением, превышающим единицу (1,01), но не достигающим порога существенности.
Значения стоимости для налогообложения остальных объектов лежат ниже соответствующих им рыночных цен. Среднее по всей выборке значение отношения «налоговая стоимость/цена» составляет 0,91, минимальное значение – 0,77.
-
2.3.5. Порядок определения базовых ставок и коэффициентов модели
-
2.4. Сравнение показателей рассмотренных моделей оценки
Для определения базовых ставок и коэффициентов методики, реализующей метод последовательных сечений, следует ориентироваться на полученные в таблицах 20, 21 и 23 коэффициенты модели.
В качестве альтернативного решения в модели последовательных сечений может быть утверждена таблица налоговых стоимостей квартир по выбранным группам последнего шага сечений, аналогичная таблице 22, но с указанием налоговой стоимости (табл. 27).
Таблица 27
Налоговые стоимости квартир в зависимости от значений основных ценообразующих признаков
|
Ценовая зона |
Стены |
Количество комнат |
Средняя цена, д. е. |
Налоговый коэффициент |
Налоговая стоимость, д. е. |
|
1 |
кирпичные |
1 |
786 |
0,91 |
716 |
|
1 |
кирпичные |
2 |
856 |
0,91 |
779 |
|
1 |
кирпичные |
3 |
964 |
0,91 |
877 |
|
1 |
кирпичные |
4 |
1057 |
0,91 |
962 |
|
1 |
блочные |
1 |
724 |
0,91 |
660 |
|
1 |
блочные |
2 |
793 |
0,91 |
723 |
|
1 |
блочные |
3 |
872 |
0,91 |
794 |
|
1 |
блочные |
4 |
942 |
0,91 |
858 |
|
1 |
деревянные |
1 |
631 |
0,91 |
574 |
|
1 |
деревянные |
2 |
780 |
0,91 |
710 |
|
1 |
деревянные |
3 |
782 |
0,91 |
712 |
|
1 |
деревянные |
4 |
844 |
0,91 |
768 |
|
2 |
кирпичные |
1 |
952 |
0,91 |
867 |
|
2 |
кирпичные |
2 |
978 |
0,91 |
890 |
|
2 |
кирпичные |
3 |
1153 |
0,91 |
1050 |
|
2 |
кирпичные |
4 |
1254 |
0,91 |
1141 |
|
2 |
блочные |
1 |
860 |
0,91 |
783 |
|
2 |
блочные |
2 |
954 |
0,91 |
868 |
|
2 |
блочные |
3 |
1027 |
0,91 |
935 |
|
2 |
блочные |
4 |
1135 |
0,91 |
1033 |
|
2 |
деревянные |
1 |
852 |
0,91 |
774 |
|
2 |
деревянные |
2 |
849 |
0,91 |
772 |
|
2 |
деревянные |
3 |
983 |
0,91 |
894 |
|
2 |
деревянные |
4 |
938 |
0,91 |
853 |
Для удобства сравнения рассмотренных моделей оценки недвижимости для налогообложения сведем основные показатели их качества в таблицу (табл. 28).
Таблица 28
|
Показатель |
Регрессионная модель |
Модель параллельных сечений |
Модель последовательных сечений |
|
Нормированный коэффициент детерминации R 2 корр |
0,88 |
0,87 |
0,90 |
|
Относительная обобщенная ошибка, % |
5,9 |
6,0 |
4,7 * |
|
Средняя ошибка аппроксимации, % |
3,3 |
3,4 |
3,0 |
|
Налоговый коэффициент при 2процентном уровне существенных превышений |
0,90 |
0,90 |
0,91 |
|
Среднее значение отношения «налоговая стоимость/цена» |
0,90 |
0,90 |
0,91 |
* Среднее значение.
Как следует из таблицы, основные показатели сравниваемых моделей достаточно близки.
-
3. Формальные методы проверки выбора влияющих факторов
-
3.1. Сравнение средних значений двух экспериментальных выборок
В дополнение к методам экспертных оценок выбора ценообразующих факторов можно использовать формальные методы проверки правильности их выбора. Учитывая специфику формирования рассмотренной регрессионной модели (использование только двоичных переменных), к ним некорректно применять методы корреляционного анализа для выявления мультиколлинеарности влияющих факторов. При изменении значения двоичной переменной фактически происходит сдвиг среднего значения выходной переменной (стоимости) в подвыборке. Поэтому при анализе правильности выбора ценообразующих факторов нас прежде всего будут интересовать методы сравнения параметров двух выборок. При этом наибольший интерес, особенно в условиях ограниченного объема выборки, представляют непараметрические методы и критерии. Под непараметрическими будем понимать такие методы и критерии, которые для свой реализации не требуют соответствия функции распределения исследуемой величины (в нашем случае – цены) какому-либо параметрическому семейству функций распределения (нормальному, логарифми-чески-нормальному, экспоненциальному и т. п.).
При значительных объемах рыночных данных (более ста объектов) возможно применение классических методов, основанных на применении методов дисперсионного анализа. Это следует из того, что регрессионные модели, не содержащие иных, кроме фиктивных, переменных, по своему содержанию тождественны дисперсионной модели, а используемые им классические распределения (Стьюдента, Фишера) асимптотически сходятся к нормальным.
Типовой задачей контроля обоснованности разбиения экспериментальной выборки на однородные группы является установление совпадений или различий характеристик двух групп экспериментальных данных. Для этого формулируются статистические гипотезы:
Критические значения приводятся, как правило, для нескольких значений уровня значимости, под которым понимается вероятность ошибки, заключающейся в отклонении
(непринятии) нулевой гипотезы, когда она верна, то есть вероятность того, что различия сочтены существенными в то время, когда они случайны. Поэтому обычно критическое значение критерия определяется на уровне значимости, принятом в конкретной области знаний. В эконометрических расчетах, как правило, принимается уровень значимости a = 0,05, то есть допускается не более чем 5-процентная вероятность описанной ошибки.
Если полученное при обработке экспериментальных данных эмпирическое значение критерия оказывается меньшим или равным критическому, то принимается нулевая гипотеза, то есть считается, что различия в характеристиках сравниваемых выборок обусловлены случайными факторами. В противном случае (если эмпирическое значение критерия строго превышает его критическое значение) нулевая гипотеза отвергается и прини- мается альтернативная гипотеза, состоящая в том, что характеристики сравниваемых выборок различаются с вероятностью p =1 - a.
Для ограниченного, но не малого объема выборки ( n > 10), проверку надежности различий средних значений двух независимых выборок целесообразно проводить с помощью критерия Крамера-Уэлча, не требующего для своего применения, в отличие от известного t -критерия Стьюдента, выполнения условий нормальности распределения, равенства объемов и дисперсий сравниваемых выборок10.
Эмпирическое значение Tэмп критерия Крамера-Уэлча:
T эмп
x - y^n
V n x s x + n x s y
где x , sx 2 , nx и y , s y 2 , ny – средние значения, выборочные дисперсии и объемы первой и второй выборок соответственно сравниваются с критическим значением критерия, равным T 005 =1,96 для уровня значимости a = 0,05.
Рассмотрим в качестве примера решения практических задач, возникающих при построении моделей оценки стоимости на примере экспериментальных данных, использованных при построении моделей.
-
3. 1.1. Предположим, что мы сомневаемся и хотим проверить статистическую значимость различия в средних ценах однокомнатных ( y = 792 д. е.) и двухкомнатных ( x = 870 д. е.) квартир экспериментальной выборки (табл. 29).
Таблица 29
|
Квартира |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
1-комн. |
800 |
802 |
750 |
760 |
798 |
804 |
713 |
715 |
727 |
740 |
635 |
600 |
640 |
620 |
|
2-комн. |
880 |
805 |
860 |
880 |
780 |
810 |
788 |
900 |
740 |
700 |
850 |
1033 |
1050 |
970 |
|
Квартира |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
|
1-комн. |
650 |
642 |
960 |
962 |
912 |
958 |
966 |
870 |
840 |
850 |
880 |
777 |
780 |
1000 |
|
2-комн. |
960 |
930 |
955 |
850 |
860 |
866 |
840 |
830 |
– |
– |
– |
– |
– |
– |
Согласно исходным данным (см., например, таблицу 26) объемы выборок, содержащих однокомнатные и двухкомнатные квартиры, составляют nx = 28 и ny = 22 соответственно. Выборочные дисперсии определяются по соотношению (7), приведенному в пункте 2.1.5, где в качестве текущих значений цен ( yi ) используются соответственно цены однокомнатных и двухкомнатных квартир ( m = 0). Расчетные значения дисперсий равны s x 2 = 13 761 и s y 2 = 7 665 соответственно11.
Тогда значение Т эмп = (870 - 792) х
У 28 х 22
У 28 х 7665 + 22 х 13761
= 2,72 > T0.05 =1,96, что
позволяет отвергнуть нулевую гипотезу и с вероятностью не менее 0,95 полагать, что различия в средних значениях цен однокомнатных и двухкомнатных квартир в исследуемой выборке являются статистически надежными.
-
3. 1.2. Аналогичный результат может быть получен при применении методов однофакторного дисперсионного анализа, реализованного в пакете прикладных программ MS Excel с использованием встроенного статистического пакета «Анализ данных» и «Инструмент анализа» – однофакторный дисперсионный анализ (табл. 30). При этом в качестве входного интервала нужно указать массив данных результирующего показателя (цены), отсортированного по отдельным значениям исследуемого качественного фактора, то есть две нижние строки таблицы 29.
Для проверки гипотезы о корректности декомпозиции квартир на одно- и двухкомнатные с точки зрения влияния на величину их удельной стоимости применяется F-критерий 12.
В «Счет» таблицы 30 указано число значений цен в каждой группе, в столбце «Среднее» – среднее значение удельной стоимости каждого типа квартир, в столбце «Дисперсия» – значения дисперсий (были использованы при расчете значения критерия Крамера-Уэлча).
Таблица 30
Однофакторный дисперсионный анализ
|
Итоги |
||||
|
Группы |
Счет |
Сумма |
Среднее |
Дисперсия |
|
Столбец 1 |
28 |
22 151 |
791,1071 |
13 761,43 |
|
Столбец 2 |
22 |
19 137 |
869,8636 |
7 664,695 |
Таблица 31
Дисперсионный анализ
|
Источник вариации |
SS |
df |
MS |
F |
P-значение |
F критическое |
|
Между группами |
76 415,8 |
1 |
76 415,8 |
6,8879 |
0,011603 |
4,042647 |
|
Внутри групп |
532 517,3 |
48 |
11 094,1 |
|||
|
Итого |
608 933,1 |
49 |
В столбце 5 таблицы 31 дано расчетное значение F-критерия: Fрасч = 6,888. Соответствующее критическое значение при уровне значимости а = 0,05 приводится в седьмом столбце таблицы: Fкрит (0,05; 1; 48) = 4,043.
Если FpaC4 окажется меньше критического значения Fkpum , то с вероятностью 1 - а (где а = P-значение , указанное в столбце 6 таблицы 31) можно утверждать, что нет смысла разделять квартиры на одно- и двухкомнатные, так как подобное разделение не оказывает влияния на удельную стоимость квартиры. В нашем случае выполняется неравенство Fрасч > Fкрит , следовательно, зависимость цены от количества комнат в квартире существует, и разделение квартир на одно- и двухкомнатные является целесообразным.
При необходимости описанную процедуру проверки статистической надежности можно проводить на этапе отбора всех ценообразующих факторов. В этом случае следует установить отдельные значения (категории) каждого фактора для того, чтобы убедиться в правильности экспертного решения задачи.
При использовании этой процедуры важно помнить, что разбиваемая по категориям ценообразующих факторов выборка должна быть более-менее однородной. В противном случае вариации цены, обусловленные другими, неучтенными а, может быть, и более мощными факторами, будут приписаны действию анализируемого фактора, поэтому возможен неверный вывод о его значимости при отсутствии таковой.
-
3.2. Преобразование ценообразующих факторов
Если в качестве ценообразующего фактора используется количественная непрерывная переменная (например расстояние или площадь), то в соответствии с концепцией рас- сматриваемых моделей ее нужно разбить на градации (группы), и для каждой градации ввести отдельную фиктивную (двоичную) переменную.
Так, расстояние до метро (или центра поселения, или иного локального ценообразующего центра влияния) можно представить следующим образом: до 500 метров – х1 , от 500 до 1000 метров – х2 , более 1 километра – х3 . Тогда, если объект оценки будет находиться на расстоянии от центра влияния, например, до 500 метров, переменная х1 будет равна 1, переменные х2 и х3 будут равны 0. Если же объект оценки будет находиться на расстоянии от центра, например, от 500 до 1000 метров, переменная х1 будет равна 0, х2 – 1, х3 – 0 и т. д.
Процесс разбиения такого ценообразующего фактора можно сопровождать статистической проверкой значимости совпадения или различия средних значений исследуемой величины (в данном случае цены) в каждой из полученных градаций. Такую проверку также рекомендуется проводить с использованием критерия Крамера-Уэлча. Проверим, например, корректность разбиения расстояния до центра влияния на два интервала: до 500 метров и от 500 до 1000 метров. Допустим, что цены на однородные объекты недвижимости распределились так, как показано в таблице 32.
Таблица 32
|
Номер наблюдения |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
Цена по группам, д. е. |
До 500 м |
650 |
642 |
960 |
962 |
912 |
958 |
966 |
|
От 500 до 1000 м |
1000 |
500 |
700 |
840 |
450 |
1090 |
577 |
|
Номер наблюдения |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
|
Цена по группам, д. е. |
До 500 м |
870 |
840 |
850 |
200 |
777 |
780 |
400 |
|
От 500 до 1000 м |
300 |
– |
– |
– |
– |
– |
– |
Выполним расчеты эмпирического значения критерия Крамера-Уэлча по соотношению (11) с использованием данных таблицы 32.
Промежуточные расчеты можно выполнить с использованием статистического пакета «Анализ данных» MS Excel (табл. 33).
Таблица 33
Однофакторный дисперсионный анализ
|
Итоги |
||||
|
Группа |
Счет |
Сумма |
Среднее |
Дисперсия |
|
до 500 м |
14 |
10 767 |
769,0714 |
52 377,61 |
|
от 500 до 1000 м |
8 |
5 457 |
682,125 |
76 681,84 |
Используя полученные данные об объеме выборок ( Счет ), средних значений ( Среднее ) и выборочных дисперсий ( Дисперсия ), определим эмпирическое значение критерия Tэмп следующим образом:
Т эмп
= (769 - 682) х
_______ У14 х 8 _______
У 8 х 52378 +14 х 76682
= 0,753 < T0.05 = 1,96.
Это означает, что с вероятностью ошибки, не превышающей 5 процентов, мы можем считать совпадающими средние значения цен по группам, полученным в результате разбиения расстояния до метро на указанные градации. Другими словами, наблюдаемое различие в средних значениях цен в рассматриваемых градациях разбиения имеет случайный характер. Следовательно, такое разбиение представляется бессмысленным и надо либо перейти к иному разбиению, либо после исследования различных разбиений отказаться от применения этого признака как влияющего фактора модели.
Заключение
Оценка рыночной стоимости объектов недвижимости для любых целей как процесс состоит из изучения самого объекта оценки, рынка объекта оценки, создания экономико-математической модели рынка и собственно оценки объектов недвижимости, входящих в этот рынок.
При определении налоговой стоимости (стоимости для целей налогообложения) объектов недвижимости этот процесс дополняется важным этапом корректного определения налогового коэффициента, связывающего значения рыночной и налоговой стоимостей.
В целом алгоритм построения модели оценки стоимости можно представить в виде следующей последовательности операций:
-
• описание объекта оценки;
-
• сбор ценовой и ценообразующей информации;
-
• ценовое зонирование территории оценки;
-
• выбор ценообразующих факторов;
-
• составление таблицы наблюдений;
-
• преобразование таблицы наблюдений в цифровой вид;
-
• построение модели оценки стоимости;
-
• оценка качества модели оценки стоимости;
-
• расчет налогового коэффициента;
-
• разработка порядка определения базовых ставок и коэффициентов расчетной методики.
При создании моделей оценки стоимости объектов недвижимости для налогообложения следует искать компромисс между сложностью оценки и точностью результата. Согласно представленным расчетам точностные показатели трех рассмотренных моделей сопоставимы друг с другом. Наиболее универсальной является регрессионная модель. Однако для ее построения необходимо иметь компьютерное обеспечение и соответствующие знания математической статистики.
Практика показывает, что для оценки квартир в многоквартирных домах с целью налогообложения в качестве альтернативы регрессионному анализу при создании моделей оценки стоимости можно использовать подходы кластерного анализа методы сечений (группировок). С теоретической точки зрения методы сечений «грубее» метода регрессионного анализа. Однако за счет «сжатия» информации для них характерна высокая статистическая достоверность, простота и невысокая трудоемкость. Для использования этих моделей не требуется особых знаний в области математической статистики, не нужно создавать специальное программное обеспечение – достаточно уметь пользоваться стандартными пакетами прикладных программ. А в малых поселениях можно обойтись и без компьютера.
Расчеты доказывают, что метод последовательных сечений несколько точнее метода параллельных сечений. Кроме того, в случае применения метода последовательных сечений существует возможность территориально автономной актуализации модели оценки. Однако из-за эффекта «истощения выборки» при последовательных шагах сечения при использовании этого метода повышаются требования к общему объему экспериментальной выборки. Иными словами, если информации о ценах в каких-то группах объектов недвижимости не хватает, то для построения приемлемых с точки зрения достоверности моделей оценки стоимости недвижимости для целей налогообложения целесообразно использовать метод параллельных сечений.
Предполагается, что модели оценки стоимости для целей налогообложения будут создаваться силами местных муниципальных образований на базе местных рыночных данных. Сегодня в России насчитывается несколько тысяч муниципальных образований, что исключает возможность создания требуемого количества моделей одной группой специалистов. Задача построения стоимостных моделей может быть решена путем разработки методических рекомендаций, которые могли бы быть использованы на местах при минимальной помощи разработчиков этих рекомендаций. В связи с этим рекомендации должны быть построены по типу инструкций, минимизирующих вариативность принятия решений на этапе создания моделей на местах.
В целом представленный материал предназначен для решения именно этой задачи и является основой для ведущейся в настоящее время разработки таких рекомендаций.


