Оценка нормы производной комплекснозначной функции с выпуклой областью изменения производной второго порядка
Автор: Дмитриев Н.П.
Журнал: Вестник Нижневартовского государственного университета @vestnik-nvsu
Рубрика: Математическое моделирование и программирование
Статья в выпуске: 3, 2015 года.
Бесплатный доступ
В теории приближения функций есть немало результатов, связанных с так называемыми теоремами сравнения и неравенствами для производных на различных классах дифференцируемых функций. В дальнейшем будем рассматривать класс дифференцируемых функций с абсолютно непрерывной производной на любом отрезке прямой и существенно ограниченной производной старшего порядка. В статье [1] нами были даны оценки быстродействия действительных дифференцируемых функций с несимметричными ограничениями на вторую производную. Затем в статье [2] полученные результаты были распространены на класс комплекснозначных дифференцируемых функций с несимметричными ограничениями на вторую производную. Был рассмотрен случай, когда областью изменения производной второго порядка является эллипс, один из фокусов которого находится в начале координат. Следует отметить, что задача оценки быстродействия действительных или комплекснозначных функций тесно связана с задачей оценки норм производных таких функций. Оказалось, что в этом случае норму производной ограниченной по норме комплекснозначной функции можно оценить через сплайны Бернулли, которые были использованы в [5], или сплайны Эйлера [3]...
Сплайны эйлера, теоремы сравнения, оценка нормы производной
Короткий адрес: https://sciup.org/14116884
IDR: 14116884 | УДК: 51-7:621.1.016
Текст научной статьи Оценка нормы производной комплекснозначной функции с выпуклой областью изменения производной второго порядка
Пусть W означает класс заданных на всей числовой прямой R комплекснозначных дифференцируемых функций f(f) с абсолютно непрерывной производной / (?) на любом отрезке из R и существенно ограниченной производной второго порядка, причем
А = ||/|| = sup|/(?)|,
ess sup / (?)
Областью изменения комплекснозначной функции f^f) является центральный круг ||/||^^ радиуса К. Областью изменения производной второго порядка —2
функций класса W является некоторое выпуклое множество О, содержащее нача- Введем в рассмотрение сплайны Бер-ло координат. нулли
00 Г* с I "И ТГ / / I
/ \ /7 / 7\ 7 / 7\ 7 / ГК 1 Д)
sr ^ - a(6r+1 (с? -а^- brA (ct + d\ ЬГ(1) = Д----СТА----- k=l К
(a, с, d - специально подобранные параметры под заданные ограничения функции), которые в случае г = 2 были использованы в [5] для доказательства точного неравенства между производными действи тельной дифференцируемой функции с несимметричными ограничениями на производную второго порядка. Рассмотрим также совершенные сплайны Эйлера,
E sin((2£ +1) t - тс г / 2)
А=0 ^к+V
(/ - специально подобранный параметр под заданные ограничения функции), примененные в [3] при доказательстве теоремы сравнения и точного неравенства между производными действительной дифференцируемой функции с симметричными ограничениями на производную и-го порядка. Ясно, что параболические сплайны Эйлера z.x 1 г г ,,х 4 sin(2£ + 1)Z
г ли (Д +1)
являются частным случаем приведенных выше сплайнов Бернулли
E cosfAt — Зтг/2) „ _
-------Гз-------’ <4) к=\ к при г = 2.
Для получения двусторонней оценки нормы производной ограниченной комплекснозначной функции с областью изменения производной второго порядка в виде некоторого выпуклого множества комплексной плоскости нам понадобится алгебраическая форма сплайнов Эйлера второго порядка:
/2(0 =
t К
кК^,
[-л72, тс/2)
[л72, 3^/2)
7Г2
где ^2 = — - константа Фавара. 8
Рассмотрим эллипс
/ 2 2х/ . х2 . 2 2 2/ 2 2х
(а -с Xй +с) v =а (а -с ), где я - его большая полуось, а с - расстояние от начала координат до фокуса. Пусть прямая v - ku проходит через начало координат и точки Wp w2 на этом эллипсе (см. рис. 1).
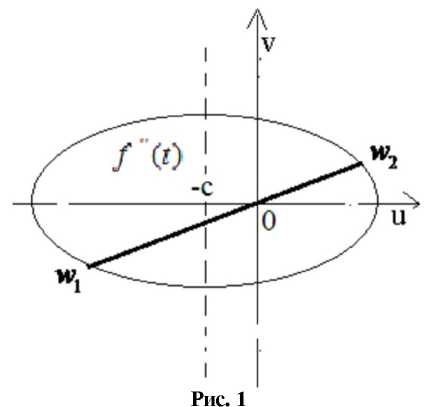
Ясно, что областью изменения производной второго порядка функции q>(t) = (p(t) -е'5, (5 = arctg к) будет отрезок [tOy, со2"\ (точнее, сами границы этого отрезка).
В [2] было доказано, что при любом к (или 5) справедливо равенство:
Ы+N Ы-Ы
= 2а
Это означает, что независимо от наклона прямой v = ku левая часть этого равенства сохраняет постоянное значение, равное диаметру эллипса. Следовательно, в качестве функций сравнения для получения оценок норм производных функций заданного класса можно использовать сплайны Бернулли, когда отрезок [й^, со2 ] совпадает с диаметром эллипса, или сплайны Эйлера,
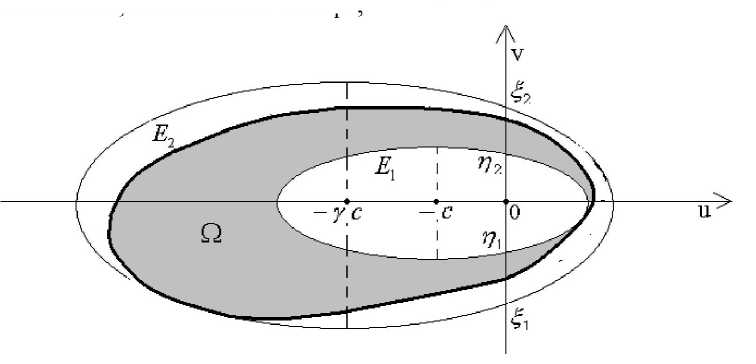
Рис. 2
когда этот отрезок лежит на мнимой оси Ov (см. рис. 1).
Рассмотрим два эллипса
Л): (и + q)2 /q2 + v2 /(q2 - q2) = 1,
/q : (w +c2 )2 / q2 + v2 /(q2 - c22)=1, где aA - большая полуось эллипса Д, q -расстояние от начала координат до фокуса этого эллипса, a q - большая полуось эллипса Е^, с2 - расстояние от начала координат до фокуса этого эллипса. Будем считать, что эллипс Ех наилучшим образом вписан в заданную выпуклую область О (например, по критерию ау —>тах, q —> min), а эллипс Е2 наилучшим образом описан вокруг области Q (например, по критерию ay > min, q —> max).
Необходимо оценить норму производной Li< f Рассмотрим функции производной <Р\(0 = [-Ч/2,Ч/2) [г| / 2, 3^ / 2) где 1^1 = |'7i| = hl, q =2 Ф2<0 = ‘ ,2 к |(7-г2)2 Г 1о /^\ [т2 / 2, Зг2 / 2) где В соответствии с рисунком 1 областью изменения функций Ф1(0 = Ф^-е1л'г и 2(Z) = будут отрезки [?7ь 7?2 ] и [^bfel соответственно. —2 Теорема. Пусть / g W такова, что 1ИНЙННИ- /'w^. Тогда Подсчитаем нормы производных функций ^(0 и ^>2(0 • Из (б) и (7) получаем: W Н(^-пХ W Wt-T^Y [-^/2,^/2) Eq /2,3^/2)’ [-т2/2,т2/2) ^2 / 2, 3^2 / 2) (Ю) Отсюда |Ы| ^Х—) = Н— = ^2(”) = l^l”-1г 1 н т 1 х 27 1 2 IIт2II т2 х 2 7 ~ 2 Подставляя ^и г2 из (б) и (7) в (8), приходим к следующим выражениям: Из уравнений описанного и вписанного эллипсов Е2, Д нетрудно получить вы- ражения модулей комплексных чисел ту, ^ через размеры этих эллипсов: 9 9 2 2 (?! а2 Таким образом, неравенство (8) в приведенной выше теореме с учетом (11) и (12) можно уточнить так: 2 2 I 9 9~ Л II II У с»! J у 4 Если выпуклая область является кругом радиуса а, то приходим к известному неравенству Адамара [4]: |[/"||< ЕКа.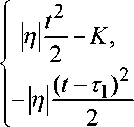
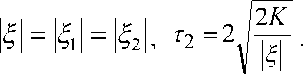
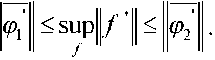
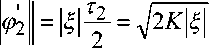
Список литературы Оценка нормы производной комплекснозначной функции с выпуклой областью изменения производной второго порядка
- Дмитриев Н.П. Оценка быстродействия динамического процесса на классе дифференцируемых функций с несимметричными ограничениями // Вестник Нижневартовского гос. ун-та. - 2013. - № 3. - С. 32-37.
- Дмитриев Н.П. Оценка быстродействия комплекснозначных функций с эллиптической областью изменения производной второго порядка // Математические структуры и моделирование. - 2015. - № 1 (33). - С. 32-37.
- Колмогоров А.Н. О неравенствах между верхними гранями последовательных производных произвольной функции на бесконечном интервале // Учен. зап. Моск. ун-та. - 1938. - Вып. 30. Математика. - Кн. 3. - С. 3-16.
- Hadamard J. Sur le module maximum d'une function et de ses derives // Soc. Math. France. Comptes rendus des Seanses. - 1914. - 41. - P. 68-72.
- Hörmander L. A new proof and generalization of an inequality of Boor // Math. Scand. - 1954. - Vol. 2. - № 1. - Р. 33-45.


