Оценка особенностей аэродинамических характеристик фюзеляжей транспортных самолётов несущей формы

Геометрические размеры и формы исследуемого фюзеляжа сопоставимы с геометрическим размерам и формам фюзеляжей самолётов тяжёлой транспортной категории. Несущий корпус самолёта условно состоит из носовой, цилиндрической и кормовой частей. Эквивалентный диаметр миделя фюзеляжа постоянен и принят d. . = 7,125 м. Корпус исходной геометрии имеет ì.ý удлинение носовой части Хн 4 = 1,5, кормовой ча сти Хк ч гДе: Х ч

= 2,7 и цилиндрической части 1„ = 4,3 , ц ч

l

= j    Хцч = -f- Хч = - к ^ [2, 3, 4].

ddd м э            м э            м э

Некруглая форма поперечного сечения фюзеляжа определяется отношением высоты h к ширине

h b его поперечного сечения h =— (рис. 1). Рассмотрено влияние значений геометрического параметра h на основные аэродинамические характеристики фюзеляжа.

Исследования проведены методом конечного объёма, базирующимся на численном решении уравнений Навье-Стокса. Для реализации этого метода применимо к поставленной задаче на основе трёхмерной геометрической модели фюзеляжа создана рабочая область, полученная путём её дискретизации на элементарные конечные объёмы [5]. Проведен анализ на сеточную сходимость: полиэдральный тип элемента сетки обеспечил необходимую точность решения при количестве ячеек области порядка 2,5×106. Количество призматических слоёв, скорость их роста, а также размер первой ячейки на поверхности модели исследуемого корпуса выбран из условия обеспечения рекомендуемого значения относительной толщины первой ячейки на поверхности у+. Обтекание несущего корпуса моделируется

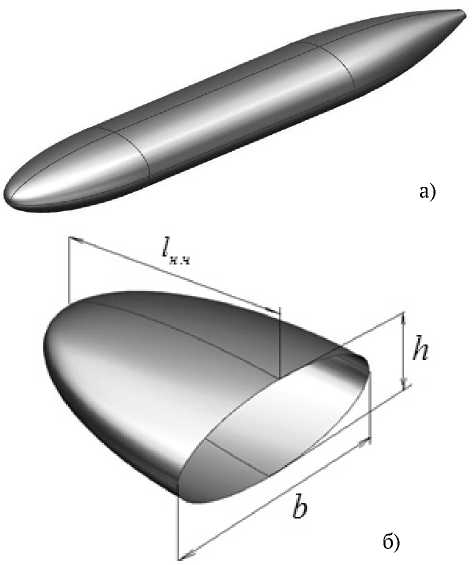
Рис. 1. Геометрическая модель несущего корпуса: а – общий вид; б – носовая часть

Производная коэффициента нормальной силы по углу атаки (рис. 3) изолированных носовых частей рассматриваемых к орпусов изменяется от значения параметра h по гиперболической зависимости. Аппроксимационная формула, описывающая эту зависимость имеет а - 1

вид: c =1,8h   . Примечательно, что при h уα

= 1 величина cу равна 1,8, что близко к значе- нию этой величины, рассчитанной по линейной теории для круглой носовой части cαу = 2 [3, 4].

Отклонение поперечной форм ы носовой части фюзеляжа от круглой формы ( h ≠ 1) влечёт за собой незначительное увеличение сопротивлени я при нулевой подъёмной силе ( ≈ на 8 % при h = 0,4), а также влияет на положение фокуса по углу атаки, положение которого можно найти по аппроксимированной зависимости

α x=- fH4

my . ^0,15      ,

—z-=k x h ’ , где k - положение cy при числе Рейнольдса Re = 3,3× 107 и числе Маха М = 0,2.

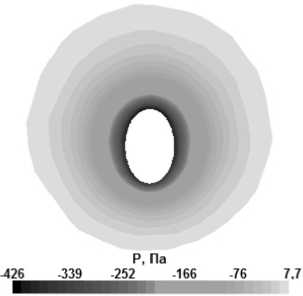
Результаты исследований приводятся в качестве распределённых и интегральных аэродинамических характеристик, как для всего фюзеляжа, так и для его изолированной носовой части. На рисунке 2 изображены поля давлений вокруг изолированных носовых частей в сечении х = 0,9 (от длины носовой части) при угле а т аки α =4^o.Поле давления вокруг носовой части с h =1 в поперечном сечении осесимметрично даже на небол ь шом угле а та ки, в то время, как при значении h <1 и даже h >1 область пониженного давления вытягивается вверх. Зависимости коэффициента нормальной силы и коэффициента продольного момента от угла атаки для изолированных носовых частей имеют линейный характер в диапазоне исследованных углов атаки (0 ≤ a ≤ 12).

геометрического центра тяжести горизонтальной проекции носовой части фюзеляжа. Установлено, что на носовых частях несущего корпуса реализуется подсасывающая сила, зависящая от угла атаки и значения параметра h .

Коэффициент подсасывающей силы носовых частей исследуемых корпусов определяется по аппроксимационной формуле: 2^-1

Ст = 0,055 ^ _н а h    , где: £ _н = 1,5 th (1 / Я н ч )

(рис. 4).

Результаты численного моделирования обтекания фюзеляжей некруглой формы показали, что введение в аэродинамическую компоновку фюзеляжа цилиндрической части ( Я ц _ч >  1,5) и сужающейся кормовой части обуславливает нелинейных характер зависимостей коэффициента нормальной силы и коэффициента продольного момента от угла атаки (рис. 5 а, 5 б). В

а)

б)

в)

Рис. 2. Поля давлений вокруг носовых частей корпуса в сечении x = 0,9 при различных h : а – h =1; б – h = 0,4; в – h = 1,5 (М = 0,2; Re = 3,3 × 10⁷; a = 4°)

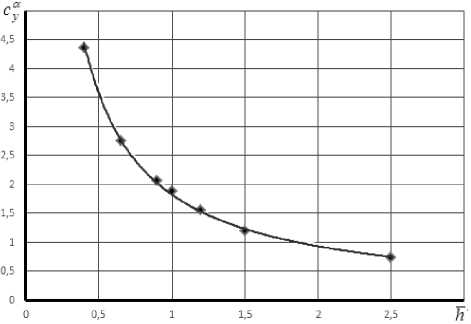
Рис. 3. Зависимость производной коэффициент а нормальной силы по углу атаки от параметра h (М = 0,2; Rе = 3×10⁷)

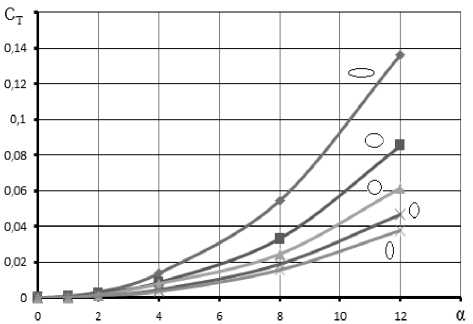
Рис. 4. Коэффициент подсасывающей силы носовых частей несущих корпусов

(М = 0,2; Rе = 3×107)

линейном диапазоне зависимости с у ( а ) (-4° = α = 4°) производная коэффициента нормальной силы по углу атаки для рассмотренных корпусов находится по зависимости с ^ = 0,8 h ^1,325 . Сужающаяся кормовая часть делает корпус статически неустойчивым в продольном и путевом каналах, что объясняется положительным значением производной коэффициентов продольного момента по углу атаки и углу рыскания, положением фокуса по углу атаки и углу скольжения впереди носка корпуса. Причём более «сплюснутые» корпуса ( h → 0) обладают меньшей степ е нью статической неустойчивости, чем круглые ( h = 0) и, тем более, «расплюснутые» корпуса ( h → ∞ ).

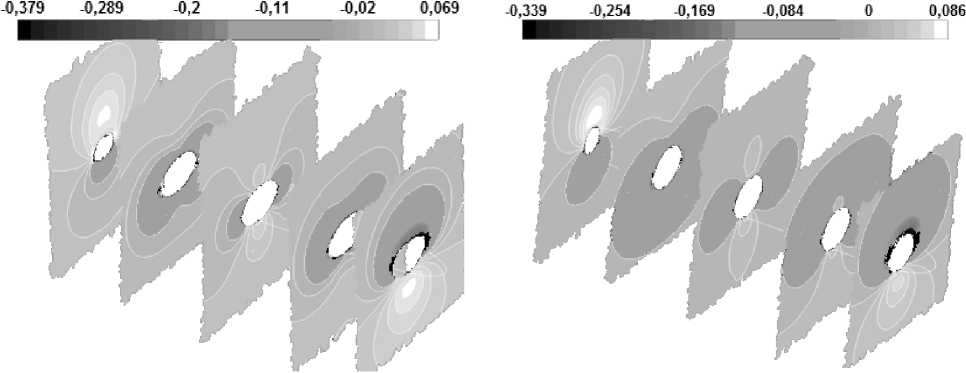
Особенности интегральных характеристик некруглых корпусов обусловлены характером распределения давления по их поверхности (рис. 6 а, б).

Анализ картин распределений давления вокруг корпусов позволяет сделать выводы:

– под сужающейся кормовой частью корпуса образуется зона пониженного давления, а над ней – зона повышенного давления; причём чем больше значение параметра h , тем больше давление над кормовой частью. Такое явление может быть причиной снижения несущих свойств фюзеляжей с большими значениями параметра 5|---------------------------- h , причиной меньших несущих свойств фюзеляжа по сравнению с его изолированной носовой частью, а также может обуславливать большую величину положительного продольного момента корпуса [2, 3, 4, 6]; причём, чем больше значение параметра h , тем ниже несущие свойства и тем больше кабрирующий момент;

– как на нижней, так и на верхней поверхностях цилиндрической части корпуса по её длине давление непостоянно, что может быть причиной участия цилиндрической части фюзеляжа в создании подъёмной силы и продольного момента;

– над н осовой частью более сплюснутых фюзеляжей h < 1 давлен и е ниже, чем над носовыми частями корпусов с h ^≥ 1, что может являться причиной повышения несущих свойств фюзеляжа за счёт придания ему сплюснутой формы.

В процессе исследований установлено, что нормирование аэродинамических коэффициентов по площади горизонтальной проекции корпуса, а не по площади миделя корпуса, существенно упрощает некоторые вышеприведенные зависимости (см. рис. 7 а, б). Таким образом, в этом случае, коэффициент нормальной силы рассмотренных корпусов в исследованном диапазоне углов атаки не зависит от длины их цилиндрической ”’, ------------------------------------------------------------

°.14------

а)                                                                  б)

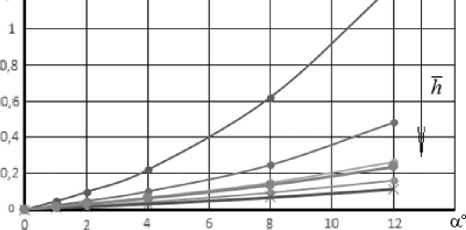
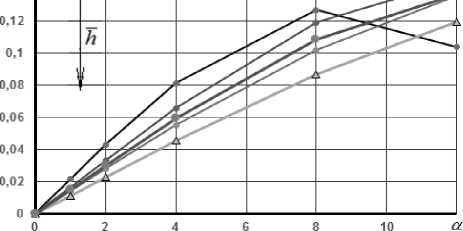
Рис. 5. Зависимости:

а – коэффициента нормальной силы;

б – коэффициента продольного момента от угла атаки при различных значениях параметра h (0,65; 0,9; 1; 1,2; 1,5)

Ср                                           ср

а)                                                                   б)

Рис. 6. Распределение коэффициента давления по п о верхности исследованных корпусов при: а – h = 0,65; б – h =1,2

а)

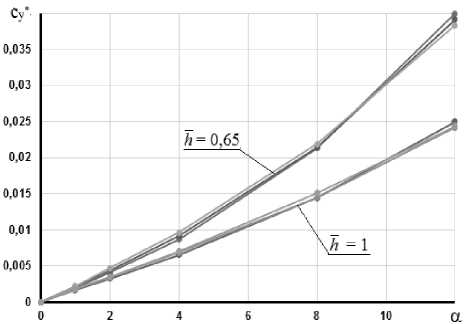
Рис. 7. Зависимости:

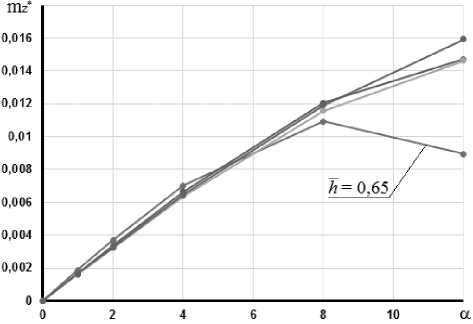
б)

а – коэффициента нормальной силы от угла атаки при различных удлинениях цилиндрической части фюзеляжа Лц 4 (4,2; 3,5; 2,7) и h = 0,65; 1

б – коэффициента продольного момента от угла атаки при различных значениях параметра h (0,65; 0,9; 1; 1,2)

части; так же от длины цилиндрической части рассматриваемого корпуса и значения параметра h не зависит коэффициент продольного момента на линейном участке диаграммы mz ( а ) . Это подтверждается тем фактом, что зависимости коэффициента нормальной силы от угла атаки рассмотренных корпусов с различными длинами цилиндрических частей накладываются друг на друга и сливаются в одну кривую (рис. 7 а). То же самое происходит и с зависимостями m z ( а ) .

Данное свойство может упростить процедуру расчёта аэродинамических характеристик корпуса самолёта, особенно, когда рассматриваются его модификации, предполагающие установку цилиндрических частей разной длины, определяющуюся длиной грузового или пассажирского отсека.

Придание фюзеляжу «сплюснутой формы» приводит к незначительному росту его сопротивления при нулевой подъёмной силе cx0, что объясняется увеличением площади смачиваемой поверхности фюзеляжа при h ≠ 0 (при постоянном миделе). Минимальное сопротивление при нулевой подъёмной силе создаёт фюзеляж круглого сечения. При приведении cx0 к площади горизонтальной поверхности корпуса зависимость cx0(h) рассмотренных фюзеляжей получает линейный характер (рис. 7).

Увеличение «сплюснутости» изолированн о го фюзеляжа рассматриваемой конфигурации ( h < 1) существенно увеличивает его аэродинамическое качество: со значения К = 0,2..0,6 при к руглой форме поперечного сечения фюзеляжа ( h = 1) до К = 0,5...2 при h = 0,4 в зависимости от угла атаки. В исследуемом диапазоне углов атаки ( α = 0..12°) аэродинамическое качество увеличивается пропорционально углу атаки при h ≥ 0,65. При h < 0,65 наблюдается отклонение от линейной зависимости в сторону уменьшения производной K ^α уже при α ≈ 8° (рис. 9).

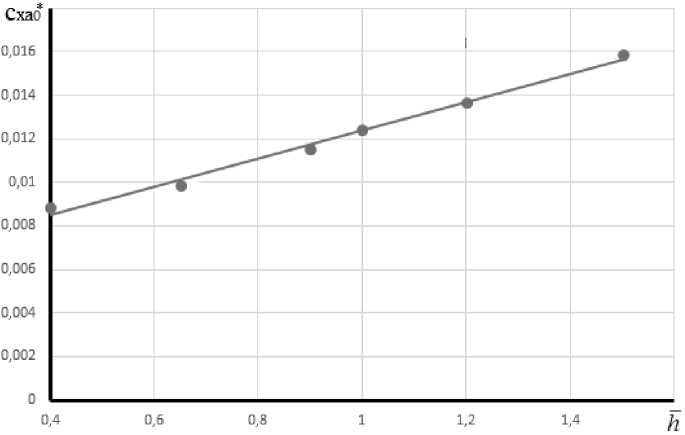
Рис. 8. Зависимость c x 0 рассматриваемых корпусов от значения параметра h

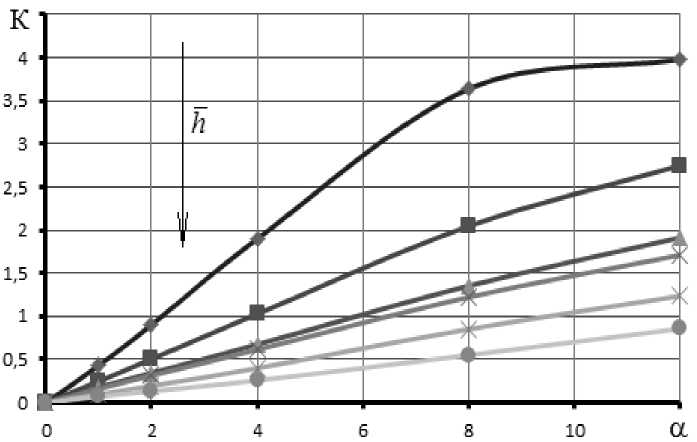
Рис. 9. Зависимости аэродинамического качества от угла атаки при различных h (0,4;0,65;0,9;1;1,2;1,5) (М = 0,2; Re = 3,3 X 10 7 )

В отличие от изолированной носовой части, у целого фюзеляжа за счёт добавления сужающейся кормовой части фокус по углу атаки смещается вперёд и часто оказывается впереди носка фюзеляжа. У исследуемых корпусов принятой геометрии производные коэффициентов нормальной силы и продольного момента остаются постоянными в довольно узком диапазоне углов атаки (а = -4. .+4°), для которого и рассмотрена зависимость положения аэродинамического фокуса по углу атаки x а (рис. f а

• 10) . Параметр h особым образом влияет на Х у .

Увеличение h сдвигает Х® вперёд, делая фюзеляж более неустойчивым. Увеличение удлинения, а значит, и длины (при постоянном миделе) цилин-дрической части (увеличение расстояния между носовой и кормовой частями фюзеляжа) приводит к смещению фокуса назад (рис. 10).

ВЫВОДЫ

Придание поперечному сечению корпуса самолёта эллиптической формы позволяет:

• -    существенно повысить несущие свойства корпуса;

• -    улучшить его аэродинамическое качество;

• -    несколько снизить степень статической неустойчивости фюзеляжа при h <1.

Эллиптическая форма поперечного сечения фюзеляжа влечёт за собой:

• -    незначительное увеличение сопротивления при нулевой подъёмной силе;

• -    смещение фокуса по углу атаки назад при h <1, и вперёд при h >1;

• -    ранее появление нелинейного участка зависимости продольного момента от угла атаки при h <1;

  

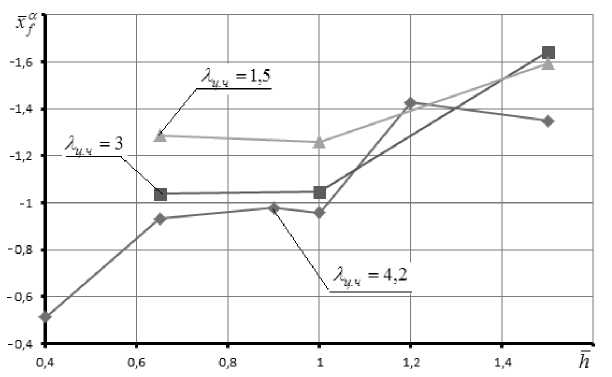
  Рис. 10. Положение аэроди н амического фокуса по углу атаки (в долях длины фюзеляжа) в зависимости от параметра h при различных удлинениях цилиндрической части фюзеляжа Х _цч = 4,2; 3; 1,5 (М = 0,2; Re = 3,3 х 10 7 )

  
  

• -    повыс и ть степень статической неустойчивости при h >1.

Выведены аппроксимационные зависимости основных аэродинамических характеристик рассмотренных несущих корпусов.