Оценка остаточного ресурса безопасной эксплуатации с учетом случайных факторов

При эксплуатации любых технических объектов происходит старение их элементов в результате различных механических, тепловых, электрических и других физико-химических процессов или под воздействием внешних и внутренних нагрузок различной природы. Эти процессы и факторы вызывают накопление повреждений, развитие дефектов, необратимые изменения свойств конструкционных материалов и параметров элементов технических объектов и, как следствие, постепенное снижение их функциональности, что впоследствии приводит к отказам и к наступлению предельного состояния, после чего дальнейшая эксплуатация невозможна.

Эффективность эксплуатации технического объекта, в первую очередь, связана с его использованием по назначению, поэтому основная задача управления процессом технического использования заключается в повышении доли времени использования при приемлемых затратах на техническое обслуживание и ремонт [1].

Современный уровень научно-технического прогресса позволяет создавать объекты, которые обладают высокой надежностью. Основой для этого служит комплекс мер, применяемых на стадиях проектирования, изготовления, монтажа и эксплуатации. Наиболее актуальной является проблема прогнозирования и обеспечения технического ресурса объекта. Общая схема оценки остаточного ресурса представлена на рисунке [2].

По результатам прогнозирования на стадии эксплуатации возможно увеличение ресурса и сроков эксплуатации элементов технических систем. Решение этой задачи предусматривает установление качественных и количественных закономерностей, определяющих ресурс, разработку методов оценки влияния различных факторов на средний ресурс и разброс ресурса эксплуатируемого объекта [1–4].

Контролируемыми параметрами могут быть как непосредственно измеряемые величины повреждений (глубина коррозии или износ детали), так и выходные параметры оборудования (производительность, коэффициент полезного действия, степень разделения, очистки) и другие количественные показатели качества. Контроль изменения этих параметров по мере приближения их значений к предельно допустимым позволяет прогнозировать момент наступления отказа [5; 6]. Оценка надежности в данном случае осуществляется путем проведения периодических обследований оборудования, измерения значений определяющего параметра, статистической обработки результатов измерений и последующего расчета показателей надежности.

Совершенствование методов расчетов требует, в частности, учета стохастической изменчивости свойств и структуры системы, а также изменчивости других случайных факторов. Необходимым этапом развития статистического подхода должна стать разработка в рамках существующих детерминированных схем расчета методики оценки надежности с учетом изменчивости свойств материала и значительной неопределенности исходных данных.

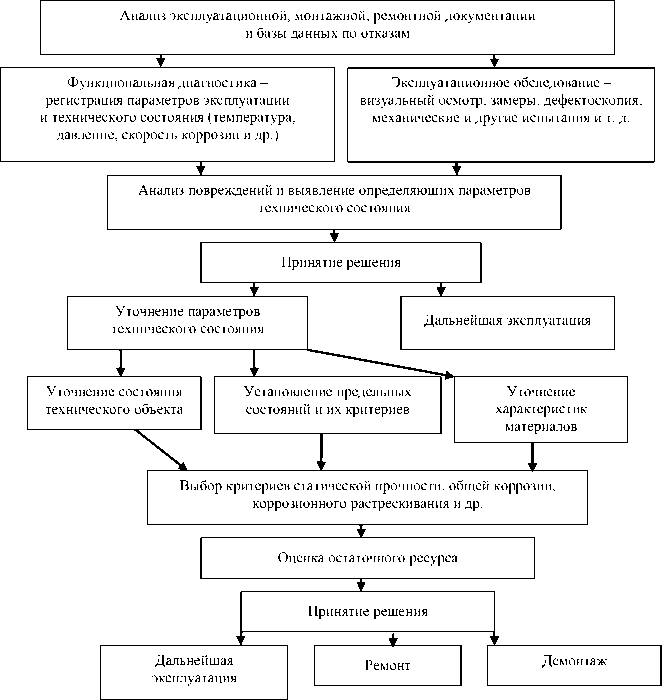
Схема оценки остаточного ресурса

В таких схемах предполагается, что данный материал имеет одинаковые значения физико-механических характеристик во всех точках «активной зоны». Однако расчет должен вестись с использованием математических ожиданий этих показателей. Ввиду ограниченности доступного объема информации о свойствах и сложности их учета, практически невозможно достоверно определить набор известных математических ожиданий характеристик. Приходится пользоваться их оценками, которые асимптотически сходятся к соответствующим истинным значениям, но фактически являются случайными величинами и имеют распределения.

Надежность системы в таком случае определяется как вероятность ненаступления ни одного из возможных предельных состояний в течение заданного срока эксплуатации.

В качестве примера выполнен расчет надежности с учетом случайных факторов по материалам экспертизы технического состояния отгонной колонны (замеры толщины стенки обечайки в 149 точках), находящейся в эксплуатации 29 лет. Технические характеристики следующие: рабочее давление – 0,6 кгс/мм² или вакуум, рабочая среда – латекс, объем – 29 650 м³, температура - от 30 до 65 ° C, фактическая толщина металла обечайки сосуда – 12 мм, с учетом поля допуска - 12 ± 0,2 мм [7].

Среднее квадратическое отклонение толщины стенок обечайки находится исходя из предположения о нормальном распределении по правилу «трех сигм»:

⁵ max ⁵ min = ^{12,2 11,8} = 0,067 мм.   (1)

Математическое ожидание ц _исх приравнивается среднему значению S _ср = 12 мм.

По результатам замеров через t = 29 лет эксплуатации определяется максимальная и минимальная толщина стенки обечайки, среднее значение ц _эксп = = S ср = 6,37 мм и среднее квадратическое отклонение:

^ эксп

max

_

min

6,84 - 5,83

= 0,17 мм.

На основе найденных значений σ исх , σ эксп и µ исх и Ц _эксп, используя генератор случайных чисел MathCAD, получено по 1 000 значений исходной и фактической толщины стенки S исх и S эксп .

При оценке ресурса по определяющему параметру X ( t ) (в рассматриваемом случае это толщина металла обечайки сосуда) обычно используется зависимость вида

X ( t ) = X 0 - y t n , (3)

где X 0 – начальное значение определяющего параметра; γ – скорость изменения параметра; показатель

степени n может принимать значения из интервала от 1 до 2 [1].

В двух предельных случаях при n = 1 и n = 2

Принимая для них нормальный закон распределения, получим

X ( t ) = X 0 - у t ,     X ( t ) = X ) — Y 1 2 .           (4)

f ( ^X 0 ) =

Тогда оценка полного T ресурса при известном значении у производится решением уравнений (4) при X = X пр , оценка остаточного ресурса при X = X эксп :

exp cty V2n

X ₀

^{2 CT} X 0

,

Xо — X   T = Xо — X у , V Y

\       1 J Ьу-0уJ f (у)=--^exp 1--^"2—

^СТ у V²ⁿ      I       ^{2 СТ} у

.

Величина предельного износа X пр определяется из условий прочности, требований нормативно-технической документации или исходя из требований безопасности.

Расчетное значение допустимой толщины металла из условий прочности определяется как

Закон распределения случайной величины X ределим как [8]:

f ( X ) =

^{2 nCT} X 0 ^СТ у

от

J exp ) -

-от I

2 ct X

^X

оп-

x exp < -

X пр

^рраб D     =    0,6 ■ 2400

2 ф ( ст _до_п - Р раб )" ^{2 Х}( ¹⁶⁸ — ^0,6 )

2 ст 2

> dX ₀ .

После преобразований получим

где Р раб = 0,6 кгс/мм² - рабочее давление; D = 2 400 мм - внутренний диаметр сосуда; ф = 1 - коэффициент прочности сварного шва; ст _доп = 168 МПа - допустимое напряжение для расчетной температуры.

Для нахождения функции определяющего параметра X ( t ) необходимо знать совместный закон распределения f ( X ) случайной величины X .

В общем случае закон распределения случайной величины X имеет вид

f ( ^X ) =

---/= exp ‘ ct _X у2л

^{[ X -Ц} X ^] ,

2 ct X

,

где

^CT X

0 x = 0 x ₀

- 1 Ц у или о x =0 x ₀ - 1 0 у ,

■СТ,, или CT¥ у           X

■^СТ у ,

F ( X ) = Р [ ( X 0 , ) D J = = JJ f ( X 0 , у ) ^dX 0 d Y .

D ( X <  x )

^{f ( X} ) = / 2     22 2 /^" "exp

V ^CT X 0 ⁺ t ■^CTJ ^{2 n}

[ ^{X -(о} X 0 ^- t ^Ц у ) J

2 (ст 2. + 1 ² -ctX) X ₀         у

или

Математическая задача определения F ( X ) сводится к решению двукратного интеграла. Для случая, когда X = X 0 + γ t , интеграл берется по области D , где X 0 + γ t <  x . Таким образом, получаем конкретные пределы интегрирования:

F ( X ) = JJ f ( X 0 , у ) dX 0 d у =

D x               1                     (7)

J f ( ^X 0 , у ) d у dX 0 .

. -от                           -

f ( ^X ) =

x exp

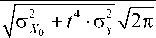
^{[ X -(о} X 0 ^- t ^2цу ) J

² ( ^CT X 0 + t ⁴ ^у )

от

= J

-от

Плотность распределения f ( X ) получим, дифференцируя по величине x , которая входит как параметр в верхний предел интеграла. Так как случайные величины X 0 и γ независимы и равноправны, плотность распределения находится как

Далее необходимо определить вид и функцию распределения ресурса. Так как вывод аналитических зависимостей представляет определенные сложности, имеет смысл решать данную задачу в численном виде. Значения t , ц _X 0 , ц _X , ст _X 0 и ст _X известны, используя формулы (14), (15) определяем Р у и ct _y:

⁰ X_o ⁰ X              ^Ц X_o ^Ц X

0 у =-------- или Ц у =----2---

или

от f ( X )=J f ( X0 )f2 ( X - X0) dX0     (8)

-от

^ст у

± ^CT XX 0    ^СТ X

t

или

^ст у

± У^ст X 0 ^СТ X t ²

от f (X)=J fl (X-у)f2 (у)dу ,        (9)

-от

где f 1 и f 2 – плотности распределения аргументов и возможные значения аргументов неотрицательны.

После определения значений р_у и ст _у с помощью генератора случайных чисел программы MathCAD получено 1 000 значений скорости изменения определяющего параметра и 1 000 значений ресурса. После проверки гипотезы о законе распределения с помо-

щью критерия Колмогорова строится функция распределения ресурса, которая хорошо аппроксимируется функцией нормального распределения:

Следовательно:

f ⁽ T ) =    ', exp

ct V2n

[ T -Ц t ]2

«               1 «

J f ( T ^dtt = —pJ exp ( - x² ) dx =

t            Vn ^     '

i « rn           „2 n          1 00 ( iV K^{2 n +1}

L f у r-nn    = 1 у IzbH—

/nJ n ^O¹              ^t-n n ! ( 2 n + 1 )

По полученным данным определены параметры функции распределения полного и остаточного ресурсов (табл. 1).

или

«f(_{T =} 1 у ^{(- 1 )} n ^{((т -P} t V^2^c t )

^J f ⁽ d = 7Л £ о        n ! ( 2 n + 1 )         ,

где n – количество членов ряда, при n = 30 погрешность составляет 10^-6.

Таблица 1

Параметры функции распределения полного и остаточного ресурсов

Зависимость	µ tп	c tn	µ t ост	c t ост
X ( t ) = X 0 - Y t	39,769	0,756	29,165	4,026
X ( t ) = X 0 - y t 2	33,959	0,322	29,013	2,006

Тогда формула (21) примет вид

X( t ) =

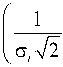
Исходя из функциональных связей между показателями безотказности, интенсивность отказов (условная плотность вероятности возникновения отказа объекта, определяемая для рассматриваемого момента времени при условии, что до этого момента отказ не возник) определяется как [9]:

t «0 ( - 1 ) n ^ ² n ⁺¹ n =0 n ! ( 2 n + 1 )

Некоторые результаты расчетов значений интенсивности отказов и остаточного ресурса приведены в табл. 2.

Ц t ) = « f ⁽ T ) ,                (20)

J f (T) dt

T

где f ( t ) – плотность распределения ресурса. Тогда для рассматриваемого случая

M t ) =

( ¹

c, V2n у t

exp

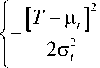
Таблица 2

Интенсивность отказа объекта

Зависимость определяющего параметра	Остаточный ресурс Т ост , лет	Интенсивность отказов X, г - 1 (ч - 1 )
X ( t ) = X 0 - Y t	42	3,68 • 10 -4 (4,21 • 10 - 8 )
X ( t ) = X 0 - y t 2	35	1,78 • 10 - 3 (2,04 • 10 - 7 )

4f

J

T у

1 c t v2n

exp

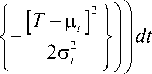
Для решения интеграла произведена замена переменных:

«

J f (T d =

1      ”

---1= J exp c _t V2n t

[t -Pt ]2 2c 2

- dt =

1 ”

= -/=J exp ( - x 2 dx , V л ^

^{T -}P;

где x = —p— , откуда t = V2c _tx + p _t ; dt = V2c _tdx и

V ^2c t

_T = ^{T P} t

^" V2ct '

Раскладывая функцию (22) в ряд Тейлора, можно записать [10]:

« f -xn Г      , й " ^{x 2} n

exP(-x2 1 t .' = t( ) ^!.      (23)

n =0 n ■         n =0

Разработанная методика позволяет определять интенсивность отказов и остаточный ресурс безопасной эксплуатации технического объекта по данным о его текущем состоянии. Результаты расчетов позволяют определять вероятность отказа объекта и минимизировать риск возникновения аварийных ситуаций при решении задач оптимизации систем технического обслуживания и обеспечивать управление безопасностью при эксплуатации потенциально опасных объектов [1; 11; 12].