Оценка ожидаемых изменений по проектным параметрам магистральных каналов земляного русла с точки зрения надежности

Бюллетень науки и практики / Bulletin of Science and Practice

Для того чтобы магистральные каналы в процессе эксплуатации выполняли свои функции на требуемом уровне, необходимо обеспечить их техническое состояние, гидравлическую эффективность и бесперебойность работы, т. е. эксплуатационную надежность [1].

Оценка эксплуатационной надежности каналов на основе исследования гидравлической эффективности, гидравлико-технических и гидравлико-эксплуатационных критериев, создания вероятностно-статистической модели, исследования показателей, влияющих на эксплуатационную надежность и использования статистических значений этих показателей отражены в работах В. С. Алтунина [2], Г. В. Железнякова [3], Ц. Е. Мирцхулавы [4], А. В. Колганова [5], В. Н. Щедрина [6] и Ю. М. Косиченко [7-9].

Для обеспечения водопропускной способности, как одного из основных показателей гидравлической эффективности каналов, изначально следует снизить чувствительность этого параметра к возможной случайности, то есть повысить обеспечение его надежности. Поэтому в период эксплуатации обеспечение надежности значений показателей, от которых зависят основные функциональные параметры каналов, должно быть высокой.

Однако, в некоторых случаях в период эксплуатации и строительства превалирование ряда факторов, влияющих на обеспечение проектных значений этих показателей (технология строительства, человеческий фактор, условия строительства и эксплуатации, инженерно- геологические условия местности и др.) не позволяет этого. На практике при эксплуатации магистральных каналов, как земляного русла, так и облицованных наблюдаются соответствующие изменения значений геометрических и гидравлических параметров, и эти изменения отражаются на их основных функциональных параметрах. Поскольку проектирование каналов выполняется в виде точечной оценки, в результате наблюдения таких изменений значение параметра носит случайный характер и рассеивается вокруг проектного значения. Расчетный расход канала, соответствующий максимальной водопропускной способности, как одной из основных функциональных параметров канала, также зависит от многих параметров и ввиду того, что на основе существующей методики проектирования определяется по точечной оценке, является случайной величиной. Определив доверительные интервалы для соответствующих параметров каналов в период проектирования, можно разработать мероприятия по повышению его гидравлической эффективности.

При этом возникает такой вопрос, можно ли прогнозировать доверительный интервал величины расхода, как одного из основных функциональных параметров, определяющий гидравлическую эффективность канала на основе проектных точечных значений? Поиск ответа на этот вопрос имеет научно-практическое значение, так как создаст благоприятные условия для подготовки соответствующих мероприятий, направленных на повышение обеспечения надежности канала с точки зрения его водопропускной способности.

Материалы и методы

Чтобы оценить гидравлическую эффективность канала с точки зрения водопропускной способности, необходимо определить водопропускную способность по соответствующей площади живого сечения потока и соответствующие граничные условия. Как известно, водопропускная способность канала зависит от площади живого сечения потока, гидравлического радиуса, уклона дна русла и коэффициента шероховатости и при проектировании рассчитывается по расчетной формуле для случая установившегося равномерного движения воды. Определение же доверительного интервала этих рассчитанных точечных значений с точки зрения обеспечения гидравлической эффективности канала, не представляется возможным при проектировании. Поскольку из-за недостатка информации в период проектирования, а также из-за отсутствия соответствующих зависимостей, относительно определения изменений, происходящих из-за влияющих факторов, при решении таких задач обычно используется метод Монте-Карло [10]. Соответственно, при решении этого вопроса была проверена возможность его применения.

За основу прогнозирования взята формула расчета расхода для установившегося равномерного движения воды в канале:

Q = ш--д = ayC^^R^i , (1)

здесь: Q — расход, м³/сек; Q — скорость потока воды, м/сек; a — площадь живого сечения, м²; C — коэффициент Шези, м^0,5/сек; R — гидравлический радиус, м; i — уклон дна русла, число.

Для применения метода Монте-Карло к решению этой задачи необходимо знать вероятностные характеристики всех параметров, входящих в формулу (1). Поэтому были использованы результаты исследований, проведенных на основе соответствующих методов исследования гидравлической эффективности и эксплуатационной надежности каналов [11, 12], на более чем 50–ти сечениях каналов земляного русла, эксплуатируемых в республике -Верхне-Карабахского канала (ВКК), Верхне-Ширванского канала (ВШК), Нового Южно-

Муганского канала (НЮМК), Старого Южно-Муганского канала (СЮМК) и Главного Муганского канала (ГМК).

Экспериментальным путем были определены вероятные характеристики и законы распределения соответствующих параметров по гидравлическим параметрам исследуемых магистральных каналов. При нормальном законе распределения доверительный интервал абсолютного изменения соответствующего гидравлического параметра за период эксплуатации (при P=0,95; α =0,05) изменялся в следующих пределах: по площади живого сечения 5,61м²<  Дю < 5,89м², по смоченному периметру 5,97м <  Дх <  6,22м, по уклону дна 0,00009<∆J<0,00017. Также было установлено, что значение соответствующего гидравлического параметра в период эксплуатации увеличивалось по сравнению с проектным значением.

Коэффициент шероховатости на исследуемых каналах земляного русла увеличивался случайным образом, и наблюдаемый минимальный интервал этого увеличения составлял на ВКК 0,021-0,027, а на ВШК 0,021-0,036. С учетом этого в качестве начальных условий принималось, что площадь живого сечения потока в канале, смоченный периметр и уклон дна подчиняются нормальному распределению, их среднее значение равно проектному точечному значению, а среднее квадратическое отклонение соответствует «скорректированному» среднеквадратичному отклонению, коэффициент шероховатости, наблюдаемый как набор произвольно меняющихся чисел в диапазоне 0,020 -0,035 в каналах земляного русла и 0,012-0,035 в облицованных каналах. В пределах этих условий была использована программа Excel и методом Монте-Карло на основе формулы (1) для установившегося равномерного потока, построена модель прогнозирования расхода. Для этого была составлена Таблица 1. Здесь коэффициент Шези при 0,1 м≤R≤5,0 м рассчитывался по формуле Н. Н. Павловского [13]. В остальных случаях можно использовать соответствующую формулу.

С =-•Ry, п

у = 2,5 • Тп - 0,13 - 0,75 • VR • (Тп - 0,10)

м ⁰,⁵

Здесь: С — коэффициент Шези, ; R — гидравлический радиус, м; у — величина, сек определенная по формуле (2), число; n — коэффициент шероховатости, число.

Процедура прогнозирования доверительного интервала максимального расхода на соответствующем участке исследуемого канала осуществлялась следующим образом:

В столбце А Таблицы 1, составленной в Excel, выбирается «Данные»-«Анализ данных»-«Генерация случайных чисел», а в таблице отображенной на дисплее: «Число наблюдений» =1, «Число случайных чисел» =1000 (по мере увеличения числа увеличивается точность) и нормальное распределение, по параметру («Параметр») среднее («Среднее») значение проектного значения по живому сечению в соответствующем сечении исследуемого магистрального канала, среднее квадратическое отклонение («Стандартное отклонение») σ =0,50, в «Выходном интервале» отмечены $A$3 (т.е. столбец А, строка 3), и нажатием кнопки «ОК» получена генерация случайных чисел по заданным условиям. В столбце Б Таблицы 1 указанная выше операция повторена для смоченного периметра канала, только среднее значение заменено проектным значением смоченного периметра по тому же сечению канала, в «Интервале выхода» отметив $В$3 и нажав кнопку «ОК» получали генерацию случайных чисел для смоченного периметра, соответствующую заданным условиям.

В столбце C Таблицы 1 вычисляется отношение столбца A к столбцу B, то есть гидравлический радиус R=ω/χ.

В столбце D вычислялся √R, для чего использовалась функция =СТЕПЕНЬ (число; степень). Для коэффициента шероховатости (n) в столбце Е с помощью функции =СЛУЧМЕЖДУ (нижняя граница; верхняя граница) от 20 до 35 в земляных каналах и от 12 до 35 в каналах бетонной и железобетонной облицовки получены генерации 1000 случайных чисел. Здесь в качестве значения коэффициента шероховатости использовалось число, увеличенное в 1000 раз.

Таблица 1 ПРОГНОЗИРОВАНИЕ РАСХОДА МЕТОДОМ МОНТЕ-КАРЛО НА ОСНОВЕ

ФОРМУЛЫ РАСХОДА ДЛЯ УСТАНОВИВШЕГОСЯ РАВНОМЕРНОГО ДВИЖЕНИЯ ВОДЫ

A    B    C    D    E    F    G    H    I    J    K    L    M

1            Наименование канала, расстояние от начала канала до поперечного сечения

Следовательно, столбец F создается путем деления чисел в столбце E на 1000. В связи с тем, что в формуле, используемой при прогнозировании, участвует знак квадратного корня и чтобы не получить отрицательное число при генерации случайных чисел, проектное значение прогнозируемого параметра было увеличено в требуемой размере (например, в 1000 раз). С помощью функции =СТЕПЕНЬ (число; степень) в столбце G, вычислялся квадратный корень данных из столбца F. Для определения коэффициента Шези использовалась формула Н. Н. Павловского (2), а за значение параметров, входящих в формулу, принимались числа, сгенерированные в соответствующих столбцах Таблицы 1. Рассчитанные значения коэффициента Шези отражаются в столбце Н.

Принимая в столбце I Таблицы 1 за среднее значение уклона дна канала число 10 000 или 100 000-кратное его проектному значению (в зависимости от проектного значения), аналогично предыдущему порядку получают генерацию случайных чисел для случая нормального распределения. Во столько раз увеличен уклон дна русла в столбце I Таблицы 1, во столько же раз уменьшен в столбце J (например, в 10000 или 100000 раз).

Таким образом, на основе случайных чисел, сгенерированных по соответствующему закону распределения, в столбце К Таблицы 1 были рассчитаны квадратный корень чисел столбца J, по формуле Шези скорость потока в столбце L, а в столбце М расход.

После этого на основании расчетных значений расхода, согласно методике определения математического ожидания количественного знака а при нормальном распределении X для случая, когда не известно среднее квадратическое отклонения о , для расчета доверительного интервала использовалась следующая формула [14, 15]:

xs — t(P; к) • — < а < xs + t(P; к) • —,

Здесь: X_s - среднее выборочное, число; t(P; к) - коэффициент, полученный из соответствующей таблицы, число; P- доверительная вероятность, в д. е.; к-степень свободы, к = п — 1 , число; S - “скорректированное” среднее квадратическое отклонение, число; п -количество опытов (замеров) , число.

Доверительный интервал для неизвестного среднего квадратического отклонения (о) определяется по ниже следующей формуле:

S - Z_h S - Z_b ,

Здесь: S — «скорректированное» среднее квадратическое отклонение, число; Z_H = Z_H(P;k) и Zв= Zв(P; k) — соответственно нижний и верхний пределы, определяются по соответствующей Таблице; k — степень свободы, k = n — 1, (n- число замеров); при k>100, соответствующие пределы можно приблизительно рассчитать по следующей формуле [ 14 ] :

Zh = (1 +

црЖ- 1

Vk )   ■

Z b = (1

t(P)V2 - 1

Vk )   '

Здесь,t(0,95) = 1,96; t(0,99) = 2,58

Результаты и обсуждение

Прогнозирование водопропускной способности каналов по предлагаемой методике показало, что случайное рассеивание показателей, от которых зависит расход, вокруг точечных проектных значений является причиной тому, что определяемое среднее значение расхода отличается от проектного значения канала, и проведение соответствующих прогнозов в этом направлении возможно лишь в период проектирования. Принимая закон распределения как нормальное распределение, на основе 1000 значений расхода, рассчитанных путем генерации случайных чисел, определен доверительный интервал. Полученные результаты отражены в Таблице 2.

Таблица 2

ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ МАКСИМАЛЬНОГО РАСХОДА ИССЛЕДУЕМЫХ МАГИСТРАЛЬНЫХ КАНАЛОВ, ПРОГНОЗИРУЕМОГО НА ОСНОВЕ МЕТОДА МОНТЕ-КАРЛО

№	Наименование каналов	Место расположения поперечного сечения от начала канала, км	Расход нормальный брутто, по проекту, Q№ . 6 . , м3 сек "	Прогнозируемый доверительный интервал, при P=0,95, a =0,05
				По расходу, Qe, м3/сек	По среднеквадратическому отклонению, a , м3/сек
1.	САК	0,00-11,22	55,00	31,90 e< 33,14	9,60 < ст < 10,48
2.	МРЮМК*	0,00-11,22	35,00	20,83 < Qe< 21,59	5,94 < ст < 6,49
3.	АК (правобер)**	0,00-2,50	25,00	14,22 < Qe< 14,85	4,87 < ст < 5,32

Бюллетень науки и практики / Bulletin of Science and Practice Т. 8. №12. 2022

№	Наименование каналов	Место расположения поперечного сечения от начала канала, км	Расход нормальный брутто, по проекту, Q h,6, , м3 сек "	Прогнозируемый доверительный интервал, при P=0,95, α =0,05
				По расходу, Qe, м3/сек	По среднеквадратическому отклонению, σ , м3/сек
4.	ВКК	0,00-3,30	112,00	83,03 < Qe< 86,66	14,80 < и < 16,17
5.	ВШК	0,00-3,42	78,00	60,62 e< 61,97	10,45 < и < 11,41
6.	НЮМК	0,00-0,55	70,00	53,77 < Qe< 54,91	8,85 < и < 9,66
7.	СЮМК	30,00	30,00	22,24 < Qe< 22,71	3,58 < и < 3,91

Примечание:   *Машинный рукав Южно-Муганьcкого канала (МРЮМК);

**Акстафачайский канал (правобережный)

На основе Таблицы 2 можно сказать, что прогнозируемый доверительный интервал максимального расхода исследуемых каналов различается от его проектных значений, достаточно малыми значениями интервала. Например, если максимальный расход в САК равно Q_H .g. = 55,0 м³/сек , то прогнозируемый доверительный интервал изменяется в пределах: 31,90 м³/сек < Q_e< 33,14 м³/сек , а при Q_H . ₆ .. = 70,0 м³/сек в НЮМК, расположенный в земляном русле, прогнозируемый доверительный интервал изменялся в следующих пределах: 53,77 м³/сек < Q_e< 54,91 м³/сек.

Аналогичная ситуация наблюдалась и на других каналах. Поэтому для восстановления проектных параметров этих каналов возникает необходимость внесения соответствующих изменений в период эксплуатации. При строительстве и эксплуатации случайные изменения каждого из проектных параметров каналов по-разному влияют на их функциональные параметры. Связь коэффициента шероховатости канала с изменением технических параметров каналов, часто встречается на практике и влияет на гидравлическую эффективность канала. В связи с этим при условии, что интервал изменчивости каждого из остальных параметров остается одинаковым, в период возникновения случайных изменений (по изменению соответствующего интервала) в коэффициенте шероховатости русла, прогнозным методом проанализировано его влияние на расход. Поэтому в проектном значении коэффициента шероховатости русла, прогнозный средний расход, определенный на основе вероятных интервалов изменчивости других параметров, был принят в качестве базисного значения. В качестве прогнозируемого эффекта влияния коэффициента шероховатости русла на расход, было взято процентное выражение соотношения разницы между базисным значением расхода и его средним прогнозным значением, определенный изменением коэффициента шероховатости, к базисному значению. Для определения среднего прогнозного значения расхода по изменению коэффициента шероховатости, была использована генерация случайных величин по возрастающим каждый раз интервалам изменчивости коэффициента шероховатости русла, созданных в период генерации случайными величинами по вероятным интервалам изменчивости площади живого сечения, смоченного периметра и уклона дна русла.

Каждый раз, сравнивая значение расхода с принятым базисным значением, соответственно выбранному коэффициенту шероховатости русла рассчитывался эффект его влияния на расход. Таким образом, сохраняя вероятные интервалы изменчивости других параметров канала прежним, эффект влияния анализировался путем генерации чисел, соответствующих случайному изменению коэффициента шероховатости в интервале от n=0,020 до 0,036 с увеличением на 0,002. В это время в прогнозном методе была использована генерация случайных величин по следующим интервалам коэффициента шероховатости -0,020-0,022; 0,020-0,024; 0,020-0,026; 0,020-0,028; 0,020-0,030; 0,020-0,032; 0,020-0,034; 0,020-0,036 для каналов земляного русла и интервалам - 0,012-0,014; 0,012-0,016; 0,012-0,018; 0,012-0,020; 0,012-0,022; 0,012-0,024; 0,012-0,026; 0,012-0,028; 0,012-0,030; 0,0120,032; 0,012-0,034; 0,012-0,036 для каналов бетонной и железобетонной облицовки. Соответствующие анализы были проведены в головной части магистральных каналов земляного русла, на примере Нового Южно-Муганского канала и магистральных каналов с бетонными и железобетонными облицовками, на примере Самур-Апшеронского канала. На основании полученных результатов в зависимости от интервалов изменчивости коэффициента шероховатости и его среднего значения, изменение исследуемого эффекта влияния изображено комбинированными диаграммами (Рисунок).

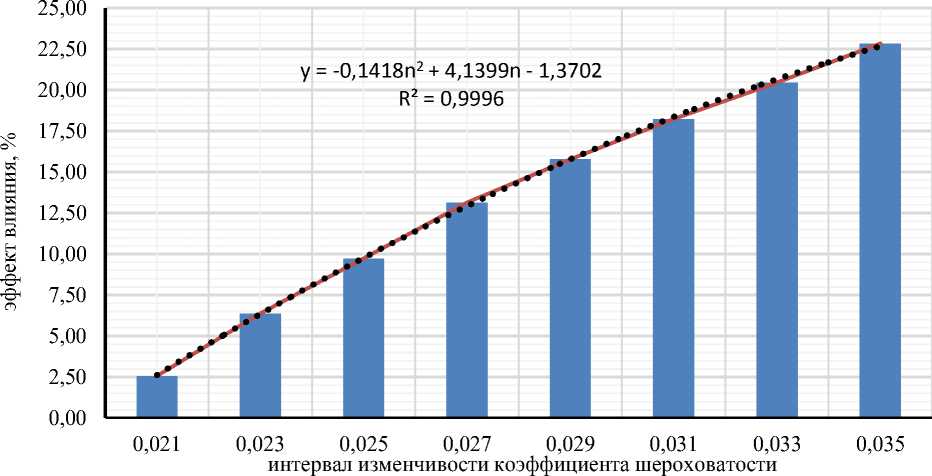
по интервалу по середине интервала полиномиальная зависимость

Рисунок. Эффект влияния коэффициента шероховатости русла на снижение расхода

На основе результатов, проведенных анализов, было определено, что при изменении коэффициента шероховатости каналов земляного русла в интервале п=0,020-0,036, каналов с бетонной и железобетонной облицовкой п=0,012-0,036, максимальный эффект влияния на расход канала будет составлять соответственно до 22% и до 39%.

На основании проведенных анализов установлено, что при коэффициенте шероховатости русла, равном точечному проектному значению, влияние соответствующих рассеиваний гидравлических параметров каналов вокруг точечного проектного значения на средний расход слабое, а при произвольном изменении коэффициента шероховатости этот эффект усиливается.

Выводы

Таким образом, на основании проведенных анализов, можно сделать следующие выводы:

• -    поскольку точечные проектные значения гидравлических параметров магистральных каналов изменяются в процессе строительства и эксплуатации, значения функциональных параметров каналов не соответствуют проектным значениям;

• -    для обеспечения совместимости значений функциональных параметров каналов с проектными значениями, изначально необходимо определить прогнозный доверительный

интервал по проектному значению каждого параметра, что возможно осуществить на основе предлагаемого метода;

• -    с учетом прогнозируемого доверительного интервала по проектным параметрам каналов, для обеспечения надежности каналов на требуемом уровне, необходимо уточнение его геометрических параметров или определив допустимый интервал изменчивости коэффициента шероховатости русла для периода эксплуатации, сохранить его под постоянным контролем в процессе эксплуатации.