Оценка параметров источника гравитационной аномалии методом роя частиц

В настоящее время методы искусственного интеллекта (ИИ) являются одним из приоритетных направлений развития науки в России и в мире. В английском языке термин artificial intelligence, в русском переводе –ИИ, означает лишь искусственное умение рассуждать разумно, а не интеллект (intellect) (Гаврилова, Хорошевский, 2000). Единого определения для ИИ не существует. Согласно А.В. Смолину (2007), «интеллектуальной называется система, способная целеустремленно, в зависимости от состояния информационных входов, изменять не только параметры функционирования, но и сам способ своего поведения». Академик В.Н. Страхов (1988) еще в конце ХХ в. писал, что в будущем необходимо «создание основ специализированного искусственного интеллекта как базовой позиции в становлении автоматической компьютерной интерпретации». Следует отметить, что геофизика является хорошо структурированной предметной областью, в которой уже существуют апробированные надежные методы, и некоторые задачи, тесно связанные с ИИ, в ней уже успешно решаются. В качестве примера можно привести алгоритмы классификации многомерных данных (Никитин, Петров, 2008) и распознавания образов (Калинин, 2011).

Метод роя частиц (МРЧ, англ. particle swarm optimization , PSO ) рассматривается в теории ИИ как метод эволюционной оптимизации (Саймон, 2020) и позволяет моделировать поведение децентрализованной самоорганизующейся системы. Первоначально этот метод был предложен для описания движения птичьих стай с целью выяснения законов, управляющих синхронным движением и быстрой сменой направления полета. С этих позиций стая птиц рассматривается как система роевого интеллекта (англ. swarm intelligence ), состоящая из множества частиц, локально взаимодействующих между собой и окружающей средой (Eberhart, Kennedy, 1995).

Текущее состояние частицы характеризуется координатами в пространстве решений, а также вектором скорости перемещения. Оба этих параметра выбираются случайным образом на этапе инициализации. Кроме того,

каждая частица хранит координаты лучшего из найденных ей решений, а также лучшее из пройденных всеми частицами решений – этим имитируется мгновенный обмен информацией между птицами. В итоге локальные и в некоторой степени случайные взаимодействия приводят к возникновению интеллектуального группового поведения, неконтролируемого отдельными особями (Казакова, 2022).

В настоящее время МРЧ широко применяется в задачах машинного обучения, параметрической и структурной оптимизации в области проектирования, в областях робототехники, биохимии, биомеханики и др. Иранские геофизики успешно использовали МРЧ для моделирования поверхности фундамента нефтегазоносного осадочного бассейна по аномальному гравитационному полю в провинции Голестан (Loni, Mehramuz, 2022). МРЧ также достаточно эффективно использовался для моделирования аномалий высших производных гравитационного потенциала, связанных с дизъюнктивными нарушениями (Elhussein et al., 2023). В отечественной литературе пока имеется единственный пример применения МРЧ при инверсии данных гравиразведки (Долгаль, 2023).

Основной теоретической предпосылкой для решения обратных задач гравиразведки (ОЗГ) с использованием МРЧ является существование множества равновероятных (в общем случае) допустимых решений, отвечающих априорным представлениям о геометрических параметрах и эффективной плотности источников поля, а также обеспечивающих требуемое значение невязки наблюденного и модельного полей с₀ (Долгаль, 2018). Рассмотрим возможность решения нелинейной обратной 2D-задачи гравиразведки рудного типа для простейшей ситуации (одиночный изолированный объект с известной эффективной плотностью) с использованием МРЧ. В частности, таким объектом может быть интрузивное тело или рудная залежь, которые требуется локализовать в разрезе.

Алгоритм метода роя частиц и результаты его применения

Будем использовать аппроксимацию аномалиеобразующего геологического объекта с известной эффективной плотностью с = const прямоугольной призмой с бесконечными размерами по простиранию, находящейся внутри области поиска решения обратной задачи D. Введем обозначения для координат {x0, z0} центра тяжести C призмы и размеров d, h ее горизонтальных и вертикальных граней соответственно. Таким образом, призма полностью характеризуется четырехмерным вектором параметров р = {х0, z0, d, h} и в дальнейшем рассматривается в качестве отдельной частицы роя (Долгаль, 2023). Рой состоит из N-частиц со случайными параметрами Pi G R4, i = 1, N, равномерно распределенными в подобласти D0 с D. Каждой частице роя соответствуют модельное гравитационное поле AgtMOfl и некоторое значение функционала F2 = ||Аднабл —

АдГ 1Ь.

Состояние всего роя характеризуется наилучшим состоянием его частиц, таким образом ОЗГ сводится к минимизации функционала min F2(p), которое осуществляется в pGD течение некоторого времени, разбитого на к = 1, М интервалов. Скорость частицы v G R10 в текущий момент времени k+1 определяется суммой трех слагаемых:

V (к + 1) = avi (к) + (SU1®[L(k) — р(к)] + yU20[G(k) — р(к)],  (1)

т.е. инерционной, когнитивной и социальной компонент. Инерционная компонента зависит от скорости частицы в предыдущий момент времени V i (к), когнитивная отражает стремление частицы к собственному наилучшему положению (локальному рекорду) L(k), социальная показывает ее движение к лучшему положению роя (глобальному рекорду) G(k). Символ 0 означает прямое (покомпонентное) произведение векторов. Длины случайных векторов U равномерно распределены в интервале [0,1], а, /?, у - коэффициенты, которые являются постоянными величинами или зависят от времени k . Схема алгоритма МРЧ показана на рис. 1. Этот алгоритм был реализован авторами в виде программы PDBR_ROI, написанной на языке Delphi 7.0 (рис. 2).

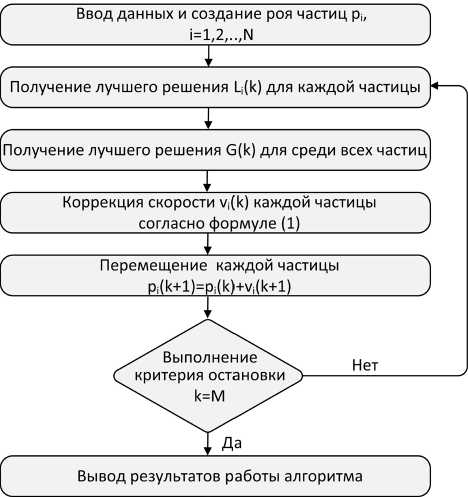
Рис. 1. Блок-схема алгоритма МРЧ

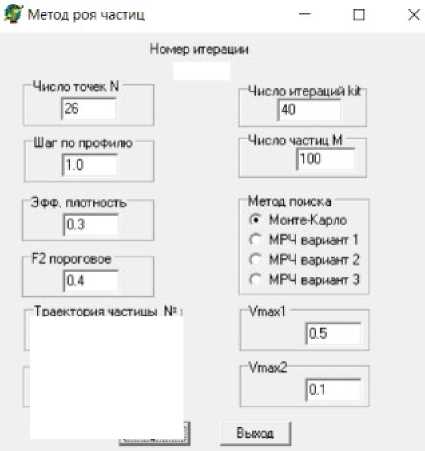
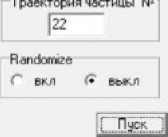
Рис. 2 . Главное окно программы PDBR_ROI

Рассмотрим синтетический пример: на профиле длиной l = 50 км зафиксирована аномалия гравитационного поля А,д^набл с амплитудой до 25 мГал, обусловленная двухмерной горизонтальной пятиугольной призмой, обладающей эффективной плотностью 0,25 г/см³. Шаг Ах между точками составляет 1 км. В области поиска решения обратной задачи D размером 50 x 25 км (разрезе) разместим N = 100 призм с плотностью 0,25 г/см³ (частиц).

На рис. 3 представлены исходные данные и начальное положение используемого роя частиц. Динамику поиска наилучшего положения частицами роя при числе итераций M = 40 отражает рис. 4. После выполнения M = 40 итераций была достигнута средняя величина невязки наблюденного и модельного полей F 2 = 0,79 мГал для всего роя частиц. Для наилучшего решения G (40) величина невязки составила 0,34 мГал, т.е. около 1,5 % от максимальной амплитуды аномалии.

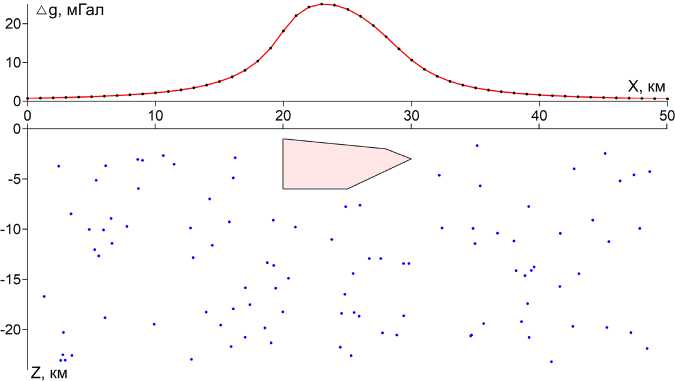
Рис. 3. График аномалии силы тяжести поля и источник поля (черный контур с заливкой). Синие точки – центры призм C для начального положения роя

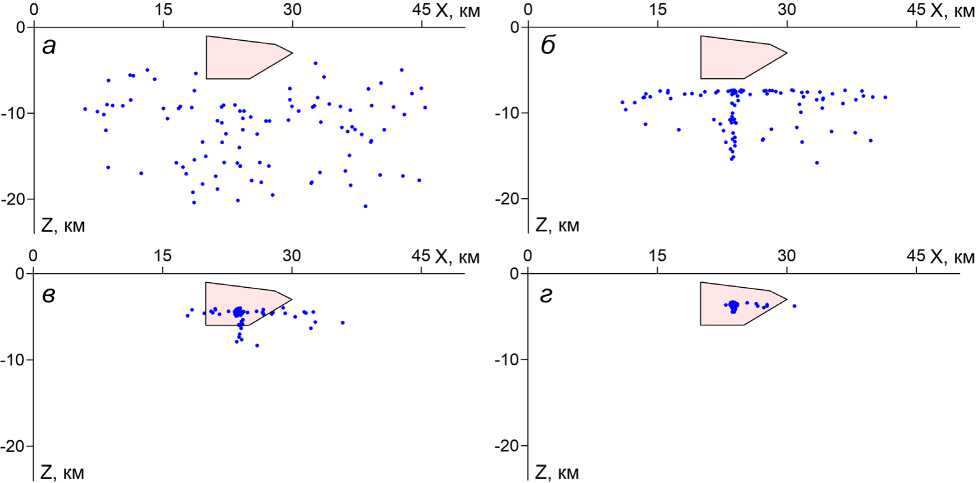
Рис. 4. Пространственное расположение центров призм C после выполнения 5 (а), 15 (б), 30 (в) и 40 (г) итераций

Устойчивость процесса оптимизации в МРЧ обеспечивает ввод ограничений на максимальные значения скорости частиц ^vi < ^vmax . Выбор величины v_m ax столь же важен, как выбор параметра регуляризации в классических методах решения обратной задачи гравиразведки, где решаются плохо обусловленные системы алгебраических уравнений. В общем случае для рассматриваемой задачи целесообразно опираться на соотношение v_max <  0,5Дх для параметров {х₀, z₀} и условие 0,9p J <  p j⁺¹ < 1,1p J ,; = 3,4 для граней призмы.

Используются 3 различных варианта изменения скоростей во времени, отвечающие выражению (1). В первом варианте используются постоянные коэффициенты «= 0,7298, ft = у = 1,4962. В втором варианте а = к(0,4 - 0,9)/М + 0,9, ft = к(0,4945 - 1,4945)/М + 1,4945, у = к(1,4945 - 0,4945)/М + 0,4945, т.е. величина ft линейно уменьшается с ростом итерации, а величина у линейно возрастает. Это позволяет сначала искать лучшее положение каждой частицы, со временем смещая акцент на лучшее положение роя. В третьем случае используется коэффициент сужения р = 0,5714, представляющий собой множитель в правой части (1), при постоянных значения коэффициентов а= 1, ft = у = 2,05:

V(к + 1) = p{avt(к) + ftU1®[L(k) -р(к)]+ yU20[G(k) -р(к)]}. (2)

Каждый из вариантов определяет собственный ход процесса оптимизации роя частиц и может иметь преимущества при решении конкретной задачи. Однако, согласно теореме NFL (no free lunth theorem), «все алгоритмы оптимизации работают одинаково хорошо при усреднении по всем возможным задачам» (Саймон, 2020), поэтому выбор варианта может быть только экспериментальным. Применительно к рассматриваемому синтетическому примеру вариант 3 заметно проигрывает по отношениям к вариантам 1 и 2 (рис. 5).

МРЧ может оказаться весьма эффективным инструментом для построения репрезентативного подмножества допустимых решений ОЗГ. Можно задаться некоторым малым пороговым значением невязки F2_nop и выбрать п частиц роя, для которых величина F2 < F2_nop. Каждую из этих частиц можно описать связной совокупностью конечных элементов ш в форме квадратов, образующих замощение области D .

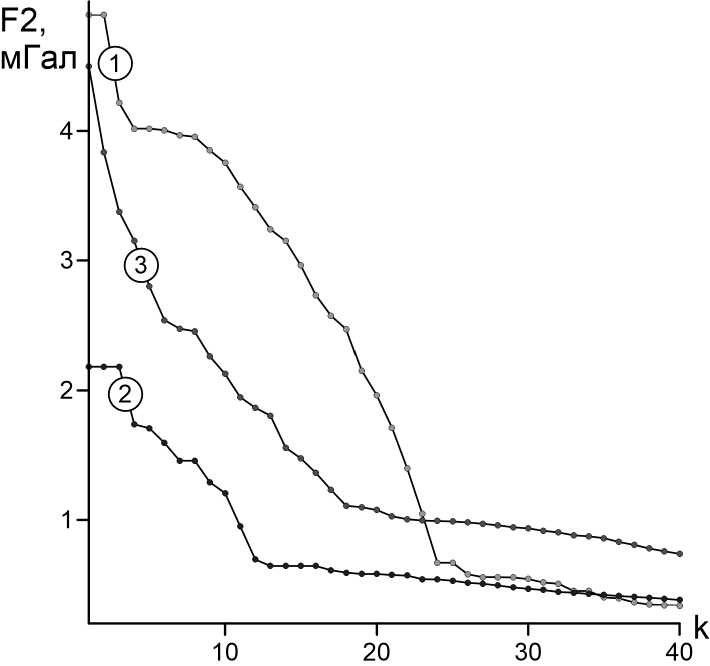
Рис. 5. Характеристики итерационного процесса различных вариантов решения ОЗГ: значения F2 отвечают глобальному рекорду G( p ). Номер варианта указан на графиках

Обозначим через п * число всех призм, в каждой из которых содержится элемент со. Тогда р = п * /п - оценка вероятности ситуации, когда элемент о является фрагментом неизвестного носителя масс (Балк, Долгаль, 2020).

Функцию пространственных координат 'ф(ы) = р(х, z) с областью определения [0,1] назовем функцией локализации, характеризующей структуру полученного множества допустимых решений ОЗГ. В качестве новой математической формы представления результатов интерпретации будем использовать одну или несколько «наилучших» результативных моделей и вертикальную карту функции локализации 1^(<о). На рис. 6 показаны результаты решения ОЗГ в варианте 1, отвечающие значению Р2пор = 0,4 мГал, числу частиц n = 28 и размеру элементов замощения 100x100 м. Как очевидно, качество выполненных интерпретационных построений высокое и является вполне достаточным для заложения заверочной скважины.

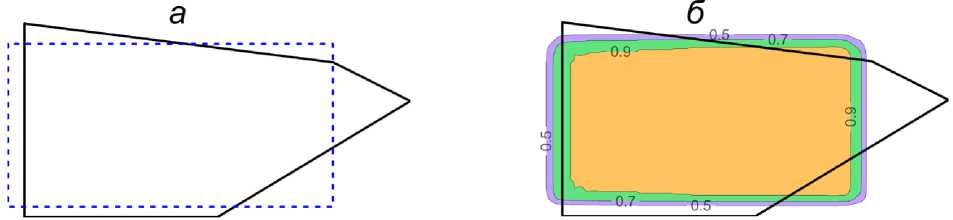
Рис. 6. Результаты решения обратной задачи гравиразведки: а – призма, отвечающая минимальному значению невязки полей F2 = 0,34 мГал (синий пунктир); б – карта изолиний функции локализации ~ф(ы). Черный контур - аномалиеобразующий объект

Приведем результаты применения МРЧ при моделировании источника Березовской аномальной зоны в пределах Юрюзано-Сыл-венской депрессии на юго-востоке Пермского края. Выполнена интерпретация данных среднемасштабной гравиметрической съемки по профилю АБ в предположении, что избыточная плотность аномального объекта равна 0.45 г/см 3 . Соотношение между протяженностью (свыше 100 км) и шириной (около 20 км) аномальной зоны допускает использование 2D-модели источников (рис. 7 а).

Размерность роя составила N = 100 частиц, их перемещение происходило в течение M = 50 интервалов времени. Величина средней невязки для роя после завершения процесса эволюционной оптимизации составила 0,70 мГал. Можно предположить, что аномалия силы тяжести обусловлена интрузивным телом ультраосновного состава мощностью ∼ 1 км, обладающим высокой избыточной плотностью и низкой намагниченностью, кровля которого располагается на глубине около 2 км от дневной поверхности (рис. 7 б).

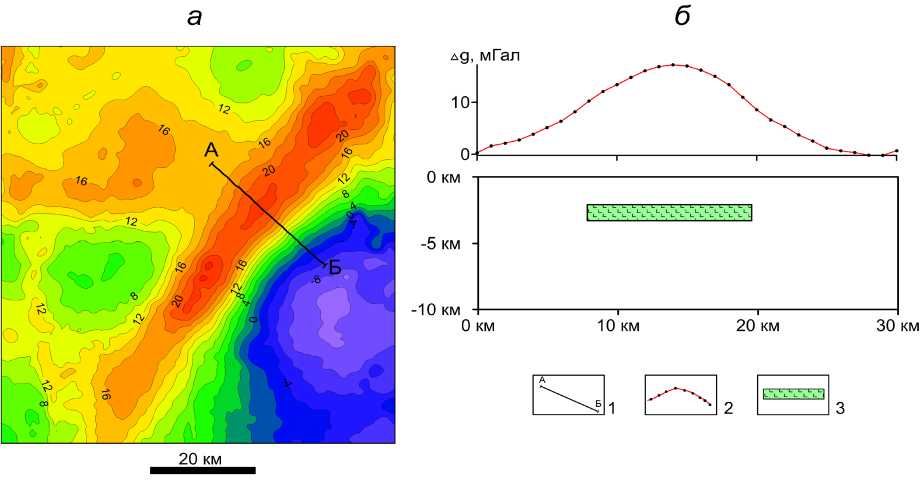
Рис. 7. Карта изоаномал гравитационного поля (а) и результаты интерпретации Березовской аномальной зоны (б): 1 – интерпретационный профиль; 2 – график наблюденного поля; 3 – модель источника гравитационной аномалии, обеспечивающая минимум невязки полей F2 = 0,69 мГал

Заключение

Полученные результаты подтверждают высокую перспективность применения МРЧ в области прикладной геофизики для моделирования источников аномалий геопотенциальных полей. Разработанный алгоритм обладает высокой скоростью сходимости, что делает возможным получение приемлемого по качеству решения ОЗГ даже при небольшом числе итераций. Нужно отметить, что для получения близких результатов с помощью метода Монте-Карло (Долгаль, Петросян, 2021) требуется примерно в 100 раз больше пробных решений прямой задачи гравиметрии.

Особый интерес представляет синтез МРЧ и аддитивных технологий количественной интерпретации геопотенциальных полей, один из примеров которого представлен выше. Дальнейшим направлением исследований в этой области является разработка модификации МРЧ для многоугольных призм, нескольких аномалиеобразующих 2D-тел и для решения 3D ОЗГ. Также может оказаться эффективным применение других методов роевого интеллекта – муравьиного и пчелиного алгоритмов, метода серых волков, гравитационного поиска и др.

Разработанная программа PDBR_ROI может использоваться студентами при выполнении лабораторных работ, что позволит им познакомиться с методикой имитационного моделирования и закрепить основные понятия из области теории решения некорректных задач математической физики. Важной особенностью программы как средства обучения является уникальный характер каждого вычислительного цикла, позволяющий судить о самостоятельном получении имеющихся результатов расчета. Программа PDBR_ROI также позволяет осуществлять решение ряда практических задач и может эксплуатироваться в производственных организациях.

Исследование выполнено при финансовой поддержке Минобрнауки России в рамках государственного задания (регистрационный номер НИОКТР 1022040500598-4-1.5.6).