Оценка параметров масс-спектрометрического пика в дублете

В ряде практических приложений элементного, изотопного и других методов анализа требуется разделить компоненты дублета — смеси двух наложившихся пиков, амплитуда одного из которых в десятки раз превосходит второй. Оценка параметров таких пиков: в мультиплетах, и в частности в дублетах, основана на математических методах восстановления сигналов, искаженных аппаратной функцией. Среди этих методов, применяемых в приборостроении, наиболее известными являются метод Тихонова [1], метод максимального правдоподобия [2, 3], метод деконволюции [4, 5], метод на основе фильтров Винера [6], метод сингулярных разложений (SVD) [7], метод наименьших квадратов [8], метод сверток [9, 10], метод независимых компонент (ICA) [11] и др. С целью подавления шума во всех этих операциях в последнее время стали использовать избыточное вейвлет-преобразование с последующей пороговой обработкой [12]. В настоящей работе на основе идеи метода ICA предлагается метод разделения пиков известной формы в присутствии шумов.

ТЕОРИЯ

Предположим, что для разделения пиков в дублете требуется по суммарному пику и положению главного пика найти положение и амплитуду второго (маленького) пика. Как правило, форма главного и искомого пиков одна и та же, но они несколько смещены друг относительно друга. Амплитуда главного пика неизвестна. Модель такого сигнала можно представить в виде x1 = Cs1 + s2,

где C — произвольная положительная константа, определяющая амплитуду главного пика, C > 10, и может быть значительно больше 10; s1 , s2 — векторы-столбцы отсчетов размерности N главного (s1 ) и искомого (s2 ) пиков. Эти пики положительны, а суммарный вектор x1 образует вектор исходных данных, как правило искаженный аддитивным шумом. Пусть известна (с некоторой точностью) форма первого пика s1 , что при известном его положении позволяет сформировать вектор-столбец модели s0 = s1. Требуется, используя эту модель и исходный сигналx1, выделить из дублета компоненту s2 . Решение, т. е. оценкуsˆ2 , будем искать в виде s2 = a x1 + b s0. (2)

С учетом выражения (2), полагая что это — точное решение, образуем скалярные произведения исходных данных:

( s ₂, x 1 ) = a ( x T • x 1 ) + b ( s T • x 1 ) = k_x1 a + k ₁₂ b ,

( ^s 2 , ^s o ) = a ( x T • ^s o ) + b ( ^s T • ^s o ) = k 21 a + k 22 b ,

которые удобно представить в матричном виде как:

f s T • X 1 ) J ^k 11

T

V ^s 2 • ^s 0 J   V ^k 21

kaa

1211 = k22 JVb JV

Построим двухстолбцовую матрицу x = ( x 1 s ₀ ) .

Используя выражение (3) легко убедиться в том, что элементы матрицы K образованы произведе-

нием x T • x . Введем далее вектор e ₁ =

' e¹¹

k e 21

и по-

ложим, что

( a )

kbJ" d

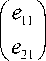
, где d — некоторая кон-

станта. Имея ввиду (1) и (2), положим a = de₁₁ = 1.

Следовательно, b = de ₂₁ = e ₂₁ 1e₁₁

r a ^и к ь

r e ¹¹ e 11 k e 21

Используя последнее выражение, покажем, что

Величина A j изменяется от A⁰ = — с шагом 0 0 _{e 11}

-A A до A max, при которой норма отрицательной составляющей оценки s_2- достигает минимума, а именно min A {||s_2-||/||s₂|}. Величину шага удобно выбирать из условия A A 0' = a | |s j ^-11|/||х₁1| при a = 0.1,...,0.5, чтобы обеспечить плавное достижение искомого минимума независимо от амплитуды главного пика.

вектор e ₁ является собственным вектором матри-

ОПИСАНИЕ АЛГОРИТМА

цы K , для которого должно выполняться равенство K e ₁ = А е ₁, где А₁ — собственное число. Действительно, продолжая равенства (4), имеем

K

Г a

k ^b

= — K e

Г e

Г e

.

k e 21 J    e l

k e 21

Следовательно, для оценки s ˆ₂ из (2) будем иметь

s ₂

e

= x +--- S o - e

Чтобы определить ошибку оценки sˆ2 и, следовательно, справедливость предположения (2), получим выражение для отношения e21 e11 . Из выражения (5) с учетом (4) будем иметь k21 e11 + (k22 - А ) e21 = 0

и e21          k21          C(s1 • so ) + (s2 • so)

e ? ( s T • s o ) - a     ■      (

Вычисление А показывает, что А < ( S T • s ₀

поэтому

e

= - C ₀, причем C ₀ >  C .

e 11

Подставляя выражение (1) в (6), с учетом последнего вывода можно убедиться в том, что компенсация главного пика при вычислении оценки s ˆ₂ происходит с избытком, т. е. в s ˆ₂ на месте главного пика будет всегда присутствовать отрицательная составляющая.

С целью устранения этой компоненты вводится итерационная процедура sj = x, + Aj-1 s0, j = 1,2,...,j

₂        1        ₀      0                      max

Алгоритм вычисления оценки ˆ2 включает выполнение следующих операций:

а) формирование вектора-столбца исходных

данных x ₁ ;

• б)    формирование вектора-столбца модели s ₀ ;

• в)    формирование матрицы x = ( x ₁ s ₀ ) ;

в) вычисление матрицы

K = (xT • x) =

xT v T k X1

• ^X 1

• ^s 0

^T s ₀

• ^X 1

A

^s 0 • ^s 0 J

г) вычисление собственных векторов e =

= ( e 1 , e 2 ) =

e 11     e 12

k e 21    e 22

(и собственных

А = ( А , А 2 ) ) матрицы K ;

д) начало итерационного цикла

значений

j = 1 от

A ⁰ = ^e 21 / ^e 11 до A 0 ^{j max};

е) вычисление оценки искомого вектора s ^j = x. + A j ^{- 1} s₀ ;

2         1         0 0

ж) подавление шума в оценке s ˆ ^j ;

• з)    вычисление на каждой итерации функционала <  j н ki ж ii;

• и)    вычисление минимума ε по нескольким итерациям. В качестве условия минимума прини-

мается выполнение неравенства

(=(j)- = ( j -2))/2< P.

где P — порог, величина которого определяется уровнем шума (например, P = с т / N + 5 •Ю ^{- 2}), σ — среднеквадратические отклонения (СКО) шума;

• к)    если условие минимума не выполняется — переход к п. (д), иначе — к п. (л);

• л)    оценка положения и амплитуды пика s ˆ₂ на итерации j - 2 .

МОДЕЛИРОВАНИЕ

Проверка качества разделения компонент дублета по предлагаемому алгоритму выполнена в среде МАТЛАБ на двух моделях исходного сигнала x 1 = C s 1 + s 2 , где векторы s 1 и s ₂ построены

• а)    по формуле ассиметричной гауссианы (задний фронт в 2 раза круче переднего);

• б)    в виде пика с плоской вершиной.

Модель пиков асимметричной гауссианы строилась по формуле:

• ^S 1 ( t ) = 4exp { - ( t - t i ) ²/ 2 p k } ,         (8)

где A ₁ — амплитуда, t ₁ — положение, µ_k — среднеквадратическая ширина пика, причем p_k = p 1 при t <  t 1 , p_k = p при t >  t 1 и P 1 >  p .

Из отсчетов функции S 1 ( t ) формируется вектор s 1 , причем компонента этого вектора S 1 i = S 1 ( i A t ) , где интервал A t выбирается из условия 50-60 отсчетов на пик. По формуле (2) формируется также вектор s ₂ с параметрами A ₂ , t ₂ , µ _{2 k} и строится модель исходных данных x 1 = C s 1 + s ₂ с добавлением белого шума с дисперсией σ ² при отношении сигнал/шум, определяемом как A ₂ σ .

На рис. 1 показан исходный сигнал х 1 ( t ) на сетке t = - 100 A t ^ 100 A t при C = 10, p = 10, A = 1, t 1 = 0, p 1 = 2P p; A 2 = 1, t ₂ = 15, p ₂ = 2P p и отношении сигнал/шум 10. Из рисунка видно, что главный пик полностью скрывает искомый пик s ₂ ( t ) . Это обстоятельство, а также наличие шума усложняют решение задачи разделения пиков.

Построим модель главного пика дублета s ₀ ( t ) , используя формулу (8) с параметрами A 0 = 1, 1 ₀ = 0, p ₀ = 2p p, сформируем матрицу x и вычислим матрицу K . Вычислим далее собственные векторы (и собственные значения) этой матрицы, используя команду eig и выполним операции в соответствии с пп. (д),…, (л) предлагаемого алгоритма .

Результат выделения искомого пика из дублета для приведенных выше исходных данных показан на рис. 1. Число итераций при этом оказалось равным 16. Итерационный процесс, который характеризуется зависимостью s ( j ) , проиллюстрирован на рис. 2.

По результатам моделирования вычислялись среднеквадратические отклонения (СКО) и смещения оценок параметров искомого пика по M реализациям шума ( M = 20):

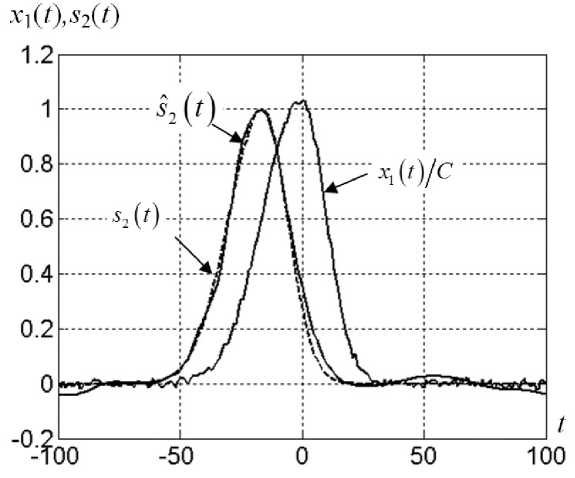
Рис. 1. Бигауссова модель дублета.

X 1 ( t ) — исходные данные; s ₂ ( t ) — искомый пик (штриховая линия); S₂ ( t ) — оценка пика (сплошная линия)

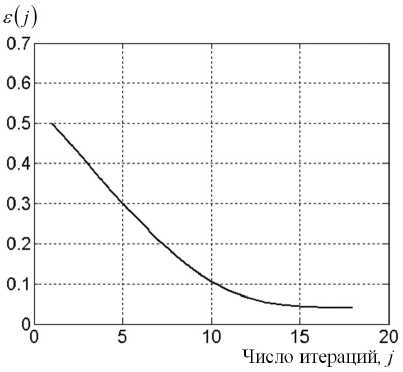
Рис. 2. Кривая сходимости итерационного процесса s ( j ) = ||s ^j ||/||s j H для бигауссовой модели при отношении сигнал/шум 10

СКО положения

M

Z( km m=1

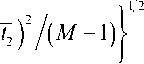
t ₂

t ₂,

смещения положения где

M 1ˆ t2  M E tm ;

^1V1- m = 1

СКО амплитуды

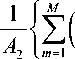
ˆ

A 2, m

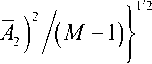
смещения амплитуды A - A , где

1 ^M

A ² 47^E A 2 m ;

m = 1

СКО восстановления формы

M ту e 1^2 - s2i m, M m=1

где норма вычисляется при каждой реализации шума.

Алгоритм был апробирован при отношении сигнал/шум от 10 и более, при C = 10 и 100. Результаты сведены в табл. 1.

Модели пиков с плоской вершиной строятся из двух пиков гауссовой формы с ц = 4 А t , расстояние между которыми такое, что образуется плоская вершина. Ширина таких пиков выбиралась равной 30 А t . На рис. 3 показан исходный сигнал X j ( t ) из пиков с плоской вершиной на сетке t = - 100 А t ^ 100 А t    при C = 10; A 1 = 1, t 1 = 0,

A 2 = 1, 1 ₂ = 10 А t , ширине пиков 30 А t . Фронты пиков — гауссовой формы при ц = 4 А t и отношении сигнал/шум 10. Из рисунка видно, что главный пик полностью скрывает искомый пик s ₂ ( t ) . Применение предлагаемой вычислительной процедуры позволило решить задачу оценки параметров скрытого в дублете пика s ₂ ( t ) , численные результаты которой приведены в табл. 2. Результат выделения искомого пика из дублета для приведенных выше исходных данных проиллюстрирован на рис. 3.

Табл. 1. Погрешность оценки параметров пика бигауссовой формы в дублете при ц = 10А t , A , = 1, t 1 = 0, ц ₁ = V2 ц ; A ₂ = 1, 1 ₂ = 15А t , ц ₂ = V2 ц

д g з s В о и и й ® К ч	О 5 и 5 О о	Погрешность оценки положения А t		Погрешность оценки амплитуды в %		СКО восстановления
		СКО	Смещение	СКО	Смещение
С= 10	10	1.4	–1.65	7.2	–0.5	0.13
	50	0.65	–1.8	3.2	–1	0.05
	Без шума	0	–2	0	–1	0.004
С= 100	10	1.7	–1.4	9	0	0.15
	50	0.65	–1.8	3.2	–1	0.05
	Без шума	0	–2	0	–1	0.004

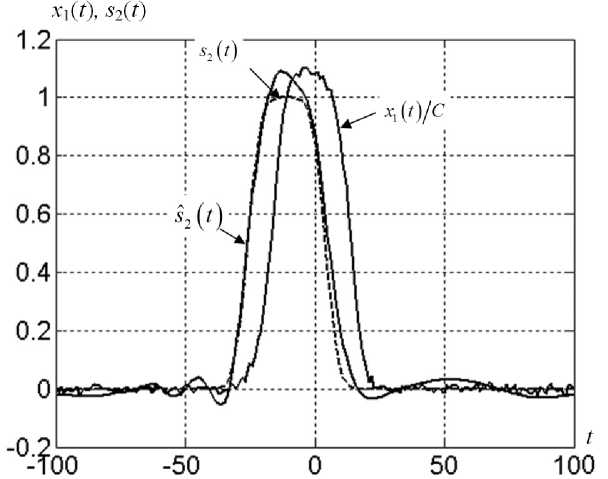
Рис. 3. Модель дублета с плоской вершиной: x 1 ( t ) — исходные данные; s 2 ( t ) — искомый пик (штриховая линия); s₂ ( t ) — оценка пика (сплошная линия)

Табл. 2. Погрешность оценки параметров пика плоской формы в дублете при A = 1, t 1 = 0, A = 1, t 2 = 10 А t .

Ширина пиков — 30 А t , фронты пиков — гауссовой формы при ц = 4 А t

з S В о % m Он сЗ	S 3 Ч О §	Погрешность оценки положения А t		Погрешность оценки амплитуды в %		м о к н О S О m о о ад t; О и
		СКО	Смещение	СКО	Смещение
С= 10	10	2.1	0.55	6	6	0.118
	50	1	0	3.2	1.2	0.035
	Без шума	0	0	0	–1	0.015
С= 100	10	2.05	0.6	7	7	0.13
	50	1.1	0	3.5	1.2	0.04
	Без шума	0	0	0	1.2	0.02

При моделировании изменялись положения главного и искомого пиков от 5 А t до 35 А t для бигаусса и от 10 А t до 35 А t для пика с плоской вершиной, т. е. от полного наложения до практически полного разделения. При максимальном разделении главного и исходного пиков для обеих моделей погрешности оценки положения и отклонения формы практически не изменились. Погрешность оценки амплитуды при этом уменьшилась на порядок.

ЗАКЛЮЧЕНИЕ

Рассмотренный метод может быть, в частности, полезен при оценке чистоты материалов, анализируемых на масс-спектрометре. Метод позволяет сделать вывод о том, существует или нет загрязнение исследуемого объекта, а если существует, то на какой массе находится сторонний объект, вызвавший загрязнение. В случае отсутствия загрязнения на месте искомого пика наблюдается только шум.

Метод оценки параметров одиночных пиков в дублетах представляет собой нелинейный итерационный процесс. Предлагаемый алгоритм быстро сходится, и он не требует аналитического описания формы пика: она может быть любой, в том числе построенной на основе экспериментальных данных.

Авторы благодарят Тимченко Н.А. за активное участие в обсуждении результатов работы.