Оценка параметров смеси сигнала с шумом по наблюдению выходов многоканального устройства различения ортогональных сигналов при когерентном приеме

Цитирование: Жиронкин, С.Б. Оценка параметров смеси сигнала с шумом по наблюдению выходов многоканального устройства различения ортогональных сигналов при когерентном приеме / С.Б. Жиронкин, А.А. Близнюк, А.А. Пшеницын, И.В. Лютиков // Журн. Сиб. федер. ун-та. Техника и технологии, 2020. 13(3). С. 361-369. DOI: 10.17516/1999-494X-0227

ных сигналов, определение точности оценок методом компьютерного имитационного статистического моделирования.

Оценка отношения сигнал/шум

При оптимальном когерентном приеме в каждом канале устройства различения сигналов находится коррелятор или согласованный фильтр, на их выходах формируются корреляционные интегралы, которые можно представить в виде

2 ^T

o

где £ ( t ) = S j ( t ) + n ( t ) - смесь принимаемого сигнала с белым гауссовским шумом с односторонней спектральной плотностью N [4].

Величины q_i имеют гауссовское распределение. При различении ортогональных сигналов q i статистически независимы, их математическое ожидание равно нулю при i + j , а при i - j - от-

2E ношению сигнал/шум Q = —, где E - энергия сигнала. Дисперсия qi также равна Q.

N

Обрабатывая совокупность q, , i = 1, M , M - количество каналов в устройстве различения ⁱ

(количество различаемых сигналов), можно получить оценку Q , не выделяя для этого специальный измерительный канал.

Известно решение классической задачи оценки по максимуму правдоподобия математического ожидания и дисперсии гауссовской случайной величины по независимой выборке [5]. Особенностью рассматриваемой задачи является то, что математическое ожидание и дисперсия равны друг другу (функция правдоподобия зависит не от двух, а от одного параметра Q ), причем математическое ожидание отлично от нуля только в одном канале, а номер этого канала неизвестен (оценивается в процессе решения задачи различения).

С учетом перечисленных особенностей наблюдение в рассматриваемой задаче может быть представлено в следующем виде:

qi = j + QQ ■ п; i = 1, M, где δij – символ Кронекера; i – номер канала в устройстве различения; j – номер принимаемого сигнала, оцениваемый в процессе решения задачи различения; n – независимые стандартные (с нулевым математическим ожиданием и единичной дисперсией) гауссовские случайные величины.

Функция правдоподобия неизвестных величин Q и j равна

p ( q i , q 2 ,...,q M I ^Q , j ) = c-— exp

2 ^ Q

( qj-Q)

2 Q

M 1

П exp

i = 1( i * j ) J2 n Q

q i

2 Q J

Функцию правдоподобия интересующего нас параметра Q находят из (1) известным способом:

M

L ( Q ) = p ( q i , q 2 ,..., q M I Q ) = £ p (^, q г ,-, q M ^Q , j ) ^P ( j ) .

j = 1

Применяя этот способ, получим

L ( Q ) = p (q, q 2qMIQ,j)(1 - Pe ( Q)) + ^ £ P ( q,,q 2qM I Q ,j), где j - оценка номера принимаемого сигнала (результат решения задачи различения); Pe(Q) -вероятность ошибки при различении сигналов.

При когерентном приеме [4]

2π

J exp

—7

Ф M ^{— 1} ( X ) dx ,

1x где Ф(x) = —j= J exp П —7

—

t2 L dt – интеграл вероятности.

Уравнение, определяющее оптимальную по критерию максимума правдоподобия оценку Q, имеет вид dQ L (Q ) = 0.

Проще найти выражение для квазиоптимальной оценки при малых значениях P ( Q ) << 1.

В этом случае L (Q). p (М    MQ) при exp

2 n Q

(q)—Q)

2 Q

MП    1exp i=1(i* j) yJ2nQ

q i

2 Q

-

Квазиоптимальную оценку Q находим из уравнения d ˆ _dQ 1 , 2 ,..., M ,

После логарифмирования и взятия производной уравнение принимает вид

—

M+21 2 i = £ j^ + 2 Q 2 ⁽ q = ^— Q ^{) 2} + Q ⁽ < ^— Q ) = 0-

В результате дальнейших преобразований приходим к приведенному квадратному уравнению

M

Q ^{2 + MQ —}£ q i ="■

Корнями этого уравнения являются

ˆ ^{MM 2 M} 2 ^Q1, 2     2 “J 4 ^+£ q i ^-

2 V ⁴     i = 1

Физический смысл имеет только первый корень, определяющий квазиоптимальную оценку отношения сигнал/шум:

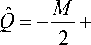
_M 2 M 2

V 4 ⁺H q i ^-

В соответствии с полученным выражением алгоритм формирования квазиоптимальной оценки инвариантен относительно результата решения задачи различения ˆ j : выходы q ˆ _i всех каналов используют равнозначно, q ˆ ˆ _j среди остальных выходов не выделяют.

Оценка спектральной плотности мощности шума

При неизвестной спектральной плотности шума корреляционные интегралы, формируемые в процессе оптимального когерентного приема, представляются следующим образом:

T

o

Величины q имеют гауссовское распределение. При различении ортогональных сигналов величины q i статистически независимы, их математическое ожидание равно нулю при i ≠ j , а

NE при i = j - энергии сигнала E (предполагается, что она известна). Дисперсия q равна---[4].

Наблюдение в рассматриваемой задаче может быть представлено в следующем виде:

NE qi=j V -

• n_t; i = 1, m ,

где δij – символ Кронекера; i – номер канала в устройстве различения; j – номер принимаемого сигнала, оцениваемый в процессе решения задачи различения; n – независимые стандартные гауссовские случайные величины.

Функция правдоподобия неизвестных величин N и j равна

Р ( q i , q 2

qM\N , j ) =

4Nne

( exp

NE     i = ¹⁽ i * ^j ) V n NE

exp

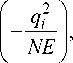
а функция правдоподобия интересующего нас параметра N –

M

L ( N ) = Р ( q i , q 2 ,..., q M \ N ) = ! Р ( q i , q 2 ,..., q M \ N , j ) P ( j ) =

= Р (., q 2,..-,qM\N,j)(1 - P( N )) + P^  М-Р ( qi, q 2  , ’m\N,A j=1( j *j)

где P_e ( N) - вероятность ошибки при когерентном различении сигналов:

”

р ( N ) = 1 - (exp V2 ⁿ -L

x

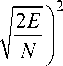
Ф ^{M - 1} ( X ) dx.

Уравнение, определяющее оптимальную по критерию максимума правдоподобия оценку

N , имеет вид

dN - L ( N ) = 0-

Выражение для квазиоптимальной оценки получим, как и в предыдущей задаче оценивания отношения сигнал/шум, в предположении о малой величине P e ( N) . В этом случае L ( N ) - P ( q i , q 2 ,..., ■, j ) при

2 A

P ( q i , q 2 ,...,         , j ) = p

’  V n NE

NE

M 1

П exp i=1(i * j) V nNE

- q^ l NEJ

-

Квазиоптимальную оценку N находим из уравнения dˆ dN p(q1,q2,...,qM\N,j 0-

Решение уравнения имеет вид

e - ² q j + Z q 2

l ^E i = 1 J

M

Такое же выражение можно получить, воспользовавшись известным результатом решения классической задачи оценки по максимуму правдоподобия дисперсии D гауссовской случайной величины по независимой выборке [5] с учетом того, что выход одного из каналов (предполагаем с номером j ) имеет отличное от нуля математическое ожидание, равное Е:

M

2    .(qj-E)+Z qi

² D = ² i = ¹⁽ i * j )

EE  M

Отсюда легко выводим (3).

В соответствии с (3) алгоритм формирования квазиоптимальной оценки спектральной плотности шума зависит от результата решения задачи различения ˆ j : помимо суммы выходов q i всех каналов отдельно используют qу

Результаты компьютерного моделирования

Точность алгоритмов формирования квазиоптимальных оценок отношения сигнал/шум и спектральной плотности шума была определена по результатам компьютерного имитационного статистического моделирования, представленного в виде графиков на рис. 1-3. По вертикальной оси на графиках нормированное (к истинному значению оцениваемого параметра) значение среднеквадратической ошибки.

На графиках рис. 1-3 видно, что, обрабатывая выходы каналов в многоканальных устройствах различения ортогональных сигналов, можно формировать практически реализуемые квазиоптимальные оценки отношения сигнал/шум или параметров шума с достаточно высокой точностью (при оценке спектральной плотности мощности шума, не зависящей ни от отношения сигнал/шум, ни от самой спектральной плотности). При увеличении объема ансамбля ортогональных сигналов точность оценок параметров смеси сигнала с шумом повышается: при M ≥ 128 среднеквадратическая ошибка снижается ниже уровня 10–15 % от истинного значения параметра.

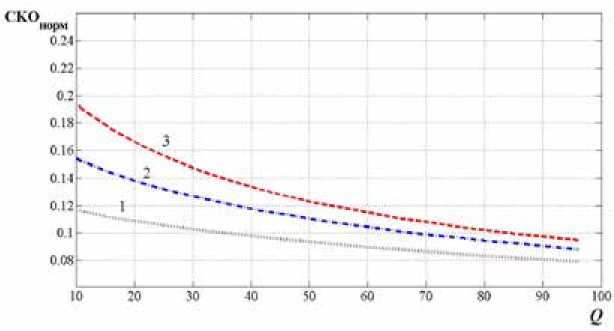
Рис. 1. Зависимость нормированного значения среднеквадратической ошибки оценки отношения сигнал/ шум от его истинного значения: 1 – для М = 128; 2 – для М = 64; 3 – для М = 32

• Fig. 1.    Dependence of normirovanny value of a srednekvadratichesky error of an assessment of the relation sig-nal/noise from its true value: 1 – for M = 128; 2 – for M = 64; 3 – for M = 32

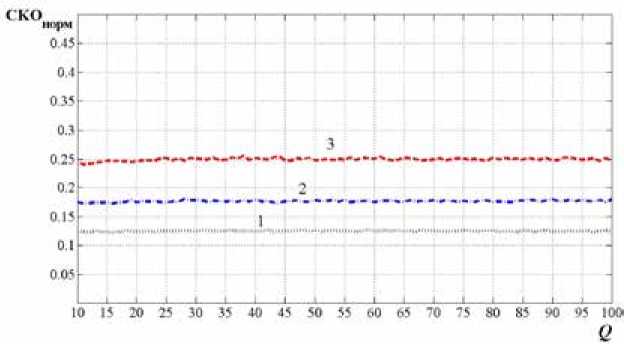
Рис. 2. Зависимость нормированного значения среднеквадратической ошибки оценки спектральной плотности шума от отношения сигнал/шум при фиксированном значении энергии сигнала: 1 – для М = 128; 2 – для М = 64; 3 – для М = 32

• Fig. 2.    Dependence of normirovanny value of a srednekvadratichesky error of an assessment of spectral density of noise on the relation signal/noise at the fixed value of energy of a signal: 1 – for M = 128; 2 – for M = 64; 3 – for M = 32

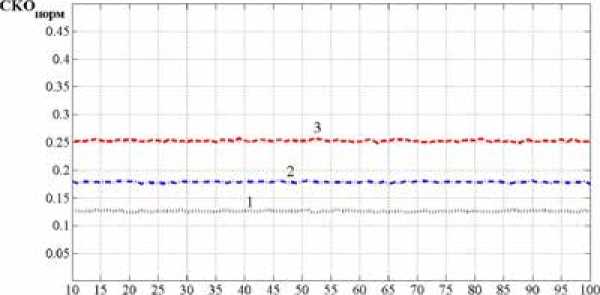
Рис. 3. Зависимость нормированного значения среднеквадратической ошибки оценки спектральной плотности шума от ее истинного значения при Q = 10: 1 – для М = 128; 2 – для М = 64; 3 – для М = 32

Fig. 3. Dependence of normirovanny value of a srednekvadratichesky error of an assessment of spectral density of noise on its true value at Q = 10: 1 – for M = 128; 2 – for M = 64; 3 – for M = 32

Заключение

Таким образом, получены математические выражения для оптимальных и квазиоптималь-ных оценок отношения сигнал/шум и спектральной плотности мощности шума, формируемых по наблюдению выходов когерентного многоканального устройства различения ортогональных сигналов. Установлено, что, обрабатывая выходы каналов в многоканальных устройствах различения ортогональных сигналов, можно формировать практически реализуемые квазиоп-тимальные оценки отношения сигнал/шум или параметров шума с достаточно высокой точностью. Эти оценки могут быть использованы для эффективной работы многих алгоритмов мягкого декодирования, управления мощностью и выделения ресурсов, реализуемых в телекоммуникационных системах. При увеличении объема ансамбля ортогональных сигналов точность оценки параметров смеси сигнала с шумом повышается, поэтому помехоустойчивость мягкого декодирования также должна повышаться. Это является дополнительным (к известным положениям [3, 4]) обоснованием целесообразности увеличения объема ансамбля ортогональных сигналов.