Оценка периода зарождения усталостной трещины от рисок после механической обработки

Под действием переменных напряжений в материалах происходит процесс постепенного накопления повреждений, приводящий к образованию трещин, их развитию и разрушению. Различают малоцикловое и многоцикловое разрушения. При малоцикловой усталости имеет место образование петель гистерезиса, поскольку циклическое деформирование происходит в упругопластической области. Число циклов до разрушения обычно не превосходит 105. Элементы конструкций во многих областях машиностроения проектируются на значительно большую циклическую долговечность. Это изделия станкостроительной и автотракторной промышленности, нефтехимического и бумагоделательного машиностроения, подъемно-транспортного и лесного машиностроения, судостроения и многих других отраслей. В связи с вышесказанным мы в дальнейшем будем рассматривать только многоцикловую усталость.

Процесс накопления повреждений делят на несколько стадий: создание характерной микро- структуры и изменение механических свойств, зарождение микротрещин в пределах устойчивых полос скольжения, распространение микротрещин и развитие их в макротрещины, образование магистральной трещины, окончательное разрушение. В расчетной практике обычно ограничиваются двумя укрупненными стадиями: стадией рассеянных повреждений и стадией развития усталостной трещины.

Продолжительность стадий зависит от материала, наличия концентраторов напряжений, размеров дефектов, степени стеснения деформаций, уровня нагруженности. В зонах местных напряжений в условиях стеснения пластических деформаций продолжительность стадии роста магистральной трещины может существенно превышать продолжительность стадии рассеянных повреждений. Так, по данным В. С. Ивановой с соавт. [1], микроскопические трещины наблюдаются уже после 0,1 числа циклов нагружения до разрушения. Относительное время развития микротрещины для образцов с концентраторами достигает 0,2…0,5 и более от общей долговечности.

В настоящее время предложено достаточно много как структурных, так и феноменологических моделей первой и второй стадии усталостного разрушения. Феноменологические (полу-эмпирические) модели основаны на обобщении результатов наблюдений и не ставят целью объяснение или полное описание существа явлений. Структурные модели позволяют описать и объяснить явления исходя из внутренней структуры рассматриваемых объектов. Используются энергетический, деформационный и силовой подходы. Силовые модели нашли наиболее широкое распространение. Заслуживают внимания кинетические уравнения повреждений силового типа и расчеты на их основе, предложенные П. А. Павловым в работе [2]. В. В. Болотиным [3] рекомендуется определять число циклов зарождения N 3 , после которого трещина начнет свое развитие при воздействии циклических напряжений постоянного размаха по формуле:

N C

N3 = -------------—, zAct > ст,    (1)

[(xAct - CTth)/ ov ] m3

где N С - постоянная времени;

X - коэффициент концентрации напряжений от микродефектов;

ct^, о th, m з - константы материала (при заданных условиях внешней среды). Константа ctv характеризует сопротивление материала накоплению микроповреждений;

CT th - порог этого сопротивления;

A ct

A CT = СТ max

напряжений

- размах

^СТ min ;

цикле;

стmax, ст min - максимальное и минимальное напряжения в цикле нагружения.

Определение периода зарождения усталостной трещины из различных концентраторов напряжений для получения расчетных оценок показателей надежности является важной задачей, так как в большинстве случаев трещина образуется именно на дефектах, являющихся концентраторами напряжений.

Формула (1) определяет число циклов, после которого трещина начнет свое развитие из микродефекта при воздействии циклических напряжений постоянного размаха A ct . При задании нагрузки в виде блока при предположении о справедливости гипотезы линейного суммирования усталостных повреждений и условия начала роста трещины

m у П = 1, у Ni используя зависимость (1), получим

N з = П б

N c CT m³

ZnXtCT- ст. ) m3

i = 1

Инкубационный период, выраженный в единицах наработки, определится по аналогии с (2) как

N c CT Im ³

Т з = Т б

m

У n(xACTi- CTth) m3

i = 1

Наработка до отказа с учетом двух стадий развития усталостной трещины запишется в виде:

T = Т з + T p ; N = N 3 + N p . ⁽⁴⁾

Число циклов N p , называемое остаточным ресурсом, определяет период распространения усталостной трещины, или живучесть.

В случае задания нагруженности в виде плотности распределения размахов действующих напряжений не представляет трудности на основе формулы (2) получить зависимость:

____________NcCT1m3____________

CT j f ( A ct )( xAct - CT th ) m³ d A ct

CT th

Определим период зарождения трещины от рисок после механической обработки. Для этого необходимо найти выражение для коэффициента концентрации напряжений x , вызванных этими рисками. В работе В. А. Пальмова с соавторами [4] решена задача теории упругости о напряженном состоянии тела со случайной шероховатой поверхностью. Решение для коэффициента концентрации при растяжении полуплоскости с синусоидальной границей, образованной системой периодически повторяющихся выступов и впадин, получено в виде:

A

X = 1 + 4nT, где A - высота выступов;

T - шаг.

В той же работе [4] рекомендуется для практических расчетов более грубая оценка коэффициента концентрации, которая хорошо согласуется с экспериментальными данными по усталости стальных образцов:

X = 1 + 4 п /2 ^a .              (6)

В рабочих чертежах на детали и элементы конструкций оговариваются параметры шероховатости поверхности и проставляется предельно допустимая высота неровностей профиля по десяти точкам R z или среднеарифметическое значение отклонения профиля от средней линии R a . Поэтому выразим коэффициент концентрации через R z . R z определяется как среднее расстояние между пятью высшими и пятью низшими точками профиля в пределах базовой длины l б [5]. ГОСТ 2789-73 распространяется на шероховатость поверхностей с интервалами R z =1600-0,025 мкм;        R a =100…0,008 мкм;

l б =25…0,01 мм. Причем для точения, строгания и фрезерования можно принять R max = 6 R a ;

Таблица 1

Расчетные коэффициенты концентрации напряжений для обработанных поверхностей

Класс шероховатости	R z , мкм	X
4	от 40 до 20	от 3,22 до 2,11
5	от 20 до 10	от 2,11 до 1,56
6	от 10 до 6,3	от 1,56 до 1,35
7	от 6,3 до 3,2	от 1,35 до 1,18
8	от 3,2 до 1,6	от 1,18 до 1,09

R z = 5 R a [6]. Здесь R max - наибольшая высота неровностей профиля. Полагая профиль шероховатостей синусоидальным со случайным значением амплитуды R z 2 и постоянным шагом l б 5, получим

X = 1 + 44,4 Rz- . (7) l б

Здесь R z входит в мм.

В таблице 1 приведены значения коэффициентов концентрации напряжений, подсчитанные по зависимости (7) при l б =0,8 мм. Они достаточно хорошо совпадают с результатами, приведенными в работе [4, с. 292, 293], где рекомендуется для 5-го класса шероховатости при обработке шлифованием коэффициент концентрации 2,44, а для восьмого класса - 1,44.

Используя (3) с учетом (7), получим зависимость для определения периода зарождения трещины от рисок механической обработки:

Т з = Т б •

N o т з

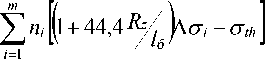
Оценивание статистических характеристик наработки до отказа в этом случае осуществляем в следующем порядке.

• 1.    Задаем число испытаний N 1 , внешнюю нагрузку и другие необходимые данные.

• 2.    Моделируем на ЭВМ по соответствующим законам распределения случайную реализацию вектора начальных параметров.

• 3.    Располагаем уровни нагрузки в блоке нагружения в случайном порядке.

• 4.    Подсчитываем период зарождения T_Ќ по зависимости (8).

• 5.    Подсчитываем по рекуррентным формулам (4.47) и (4.50), полученным в работе [7], текущие значения длины трещины и коэффициента интенсивности напряжений (КИН), сравнивая его с предельным значением K fc (или K IC ).

• 6.    Вычисления на 5-м шаге осуществляем до выполнения условия A K I > A K f _c v 1 >  l_c, после чего определяем остаточный ресурс T p .

• 7.    Определяем наработку до отказа Т = Т з + Т р .

• 8.    Повторяем вычисления по пунктам 2-6 N 1 раз для получения последовательности (выборки) { Т } объемом N 1 .

• 9.    Обработка выборки с использованием программ статистической обработки из математического обеспечения ЭВМ для оценивания средней наработки до отказа T , среднего квадратического отклонения ст ? , вероятности безотказной работы.

Полагаем 1 0 = R max/ 2 = R /2 .

При использовании аналитических зависимостей (4.40), (4.41), (4.44) и (4.45) из работы [7] для оценки длительности периода распространения усталостной трещины вместо пунктов 5 и 6 приведенного алгоритма следует применить какую-либо из вышеуказанных аналитических зависимостей.

Предложенной моделью можно пользоваться и при наличии других микродефектов. В этом случае необходимо в зависимости от них определять коэффициент концентрации х и использовать формулу (2).

Разработанные методы рекомендуется использовать при оптимальном проектировании, для задач технической диагностики, а также непосредственно в расчетах. Кроме того, они могут входить как составная часть в пакеты САПР, в экспертные системы.