Оценка погрешностей метода конечных разностей во временной области при моделировании протяженных проводников, разделенных одной ячейкой расчетной сетки

Один из основных способов моделирования протяженных проводников в методе конечных разностей во временной области [1] основан на корректировке параметров среды, окружающей проводник [2; 3]. При моделировании проводников, расположенных на расстоянии, равном одной ячейке расчетной сетки, могут возникать ошибки расчета (вплоть до возникновения вычислительной неустойчивости). Подобное расположение проводников встречается при проведении расчетов с заземлителями [4], антеннами и в прочих случаях [5; 6]. Как правило, между проводниками в таких случаях расположен источник тока или напряжения [4–6], либо проводники разделены промежутком с целью расчета напряжения между ними [5]. Поскольку данное расположение проводников встречается во многих расчетах, необходимо оценить уровень возникающих ошибок и определить возможные способы их устранения.

Материалы и методы

Все расчеты проводились при помощи метода конечных разностей во временной области (FDTD) [1]. Метод FDTD основан на решении двух из четырех уравнений Максвелла в дифференциальной форме:

—*

Vx / — = J + — , S t

——

Vx E =

sb

S t ^,

где

—*        —*

D = eE ,

——        —— в = mH ,

E – напряженность электрического поля; H – напряженность магнитного поля; D – электрическое смещение; B – магнитная индукция; J – плотность тока проводимости; ε – диэлектрическая проницаемость; µ – магнитная проницаемость.

Для устранения отражений волн от границ расчетной области в FDTD применяются т. н. "поглощающие граничные условия", являющиеся вспомогательным численным методом. В качестве поглощающих граничных условий в данной статье применяется convolutional perfectly matched layer (CPML) [1]. Толщина поглощающих граничных условий – 10 ячеек.

Условие Куранта (необходимое условие устойчивости численного решения) для метода FDTD с расчетной сеткой из кубических ячеек [1]

∆ dt ≤

где dt – временной шаг; ∆ – размер ячейки; c – скорость света в вакууме. Запишем формулу расчета временного интервала в виде

S∆

c ^

где S – безразмерный коэффициент, который не должен превышать единицу для получения устойчивого решения.

Для моделирования проводников, диаметр которых существенно меньше шага расчетной сетки, необходимо применение дополнительных методов [1]. В одном из наиболее распространенных подходов проводники располагаются вдоль узлов, в которых рассчитывается электрическое поле. Однако после задания в модели удельной проводимости протяженных проводников вдоль узлов расчетной сетки необходимо точно задать диаметр проводника. Для точного моделирования диаметра проводников корректируются значения электрического и магнитного полей в узлах расчетной сетки, находящихся в непосредственной близости от проводника. Причем корректировка производится таким образом, чтобы характер электрического и магнитного полей соответствовал полям вокруг реальных проводников [1]. В методе FDTD корректировку электрического и магнитного полей удобно производить путем изменения параметров среды. В работах [2; 3] рассматривались методы моделирования проводников. В методе [2] для моделирования проводника радиусом r корректируются значения диэлектрической и магнитной проницаемости в соответствии с формулами s’ = s- m, ц’ = ц / m,

при расчетной сетке из кубических ячеек значение m находится как m =

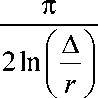
Значения параметров среды корректируются в конечно-разностных уравнениях метода FDTD, при помощи которых рассчитываются значения электрического и магнитного полей. Диэлектрическая проницаемость корректируется в узлах, радиальных к проводнику, магнитная проницаемость – в тангенциальных к проводнику узлах. В работе [3] предлагается модификация предыдущего метода, в соответствии с которой корректируются также компоненты магнитного поля, продольные по отношению к проводнику в тех случаях, когда радиус проводника меньше значения 0,208·∆. Когда радиус проводника больше 0,208·∆, корректируются продольные компоненты электрического поля. Это необходимо для устранения вычислительной неустойчивости при значениях коэффициента S, близких к единице. Также в работе [3] предложено корректировать магнитное поле на расстоянии ∆/2 от концов проводника, если радиус проводника меньше значения 0,208·∆.

Для проведения расчетов использовалась компьютерная программа, разработанная автором, обладающая основными возможностями метода FDTD и использующая дополнительные методы для моделирования протяженных проводников, источников, сред с частотной зависимостью диэлектрической проницаемости и др.

Результаты и обсуждение

Ошибки расчетов

Для демонстрации ошибок расчета проведены расчеты с дипольной антенной длиной 0,21 м (рис. 1). Дипольная антенна состоит из двух проводников, между которыми расположен источник тока. В расчетах использовался источник тока с внутренним сопротивлением 50 Ом. Диаметр проводников – 0,5 мм. Значение коэффициента S , используемое в расчетах, – 0,588. Расчеты проводились до момента времени 0,5 мкс.

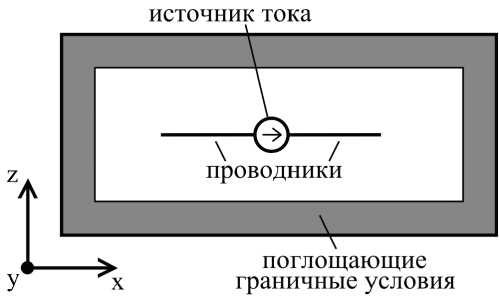
Рис. 1. Расчетная модель с дипольной антенной

Fig. 1. The calculation model with a dipole antenna

Рассчитывалось значение возвратных потерь антенны (return loss, RL _in ) для пятидесятиомного кабеля

RL in =-20log io |S_n| = -20log_M

V (o) - 50 I (rn)

V (o) + 50 1 (o)

где V (ω) и I (ω) – входные напряжение и ток. Значения V (ω) и I (ω) получены после расчетов V ( t ) и I ( t ) и применения к ним преобразования Фурье.

Форма тока источника задавалась функцией следующего вида [7]:

i(t ) =

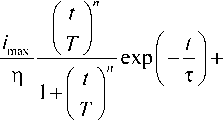
где n = 10; T = 10 ^–8 ; τ = 3·10 ^–9 ; η = 1; i max = 1 А. Ток задается после его выражения через плотность тока проводимости в уравнениях Максвелла.

Корректируемые компоненты электрического и магнитного полей представлены на рис. 2 на примере центральной части дипольной антенны, для которой проводились расчеты. Компоненты H z , H y , E z , E y корректируются согласно методу [2], за исключением компонентов, которые находятся вокруг источника тока. Компоненты E y на рисунке не показаны, все компоненты корректируются в близлежащих к проводнику ячейках исходя из симметрии. H _x – компоненты магнитного поля – предложено корректировать в работе [3]. Также в этой работе предложено корректировать компоненты магнитного поля вокруг оси проводника, отстоящие на ∆/2 от концов проводника; в данном случае они включают в себя компоненты вокруг источника тока (дополнительно корректируемые компоненты на рис. 2).

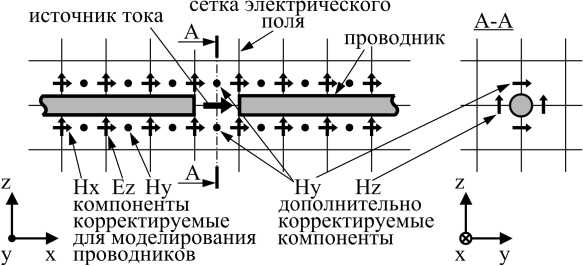
Рис. 2. Корректируемые компоненты магнитного поля

Fig. 2. Correction of the magnetic field

Напряжение V ( t ) рассчитывается как интеграл напряженности электрического поля вдоль определенного пути:

V ( t ) = J E ( t ) dl . (9)

В данном случае оно рассчитывается как произведение напряженности электрического поля между проводниками на расстояние между проводниками: E ·∆. Ток I ( t ) рассчитывается как интеграл напряженности магнитного поля вдоль контура вокруг источника тока:

I ( t ) = J H ( t ) dl. (10)

Поскольку в связи с особенностями метода расчеты выполнены во временной области, а параметр RL _in следует вычислять в частотной области, то к найденному току и напряжению, как упоминалось выше, необходимо применить преобразование Фурье и далее для каждой частоты рассматриваемого диапазона частот рассчитать значение RL _in по формуле (7).

В расчетах использованы сетки с тремя разными размерами ячеек: 10 мм; 5,12 мм; 2,593 мм. Для ячейки 10 мм проведены расчеты с корректировкой магнитного поля только у тех концов проводников, где расположен источник тока (рис. 2). Результаты расчетов представлены на рис. 3–5.

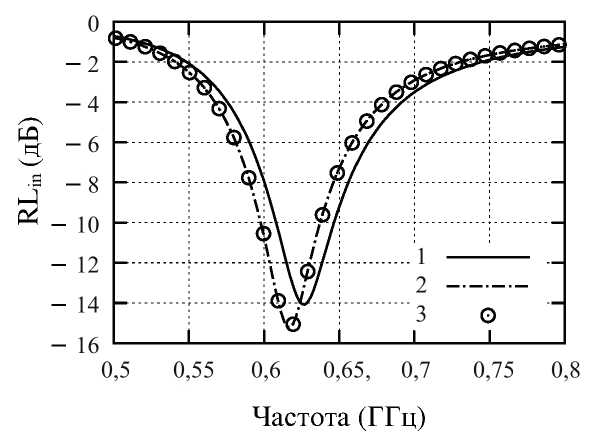
Рис. 3. Результаты расчета RL in для ячейки размером 10 мм: 1 – метод, предложенный Railton и др.;

2 – метод, предложенный Taniguchi и др.; 3 – метод, предложенный Taniguchi и др. с корректировкой магнитного поля только у источника тока

Fig. 3. The calculation results of the RL _in for the cell with the size equal to 10 mm:

1 – the method proposed by Railton et al.; 2 – the method proposed by Taniguchi et al.; 3 – the method proposed by Taniguchi et al. with the correction of the magnetic field only around the current source

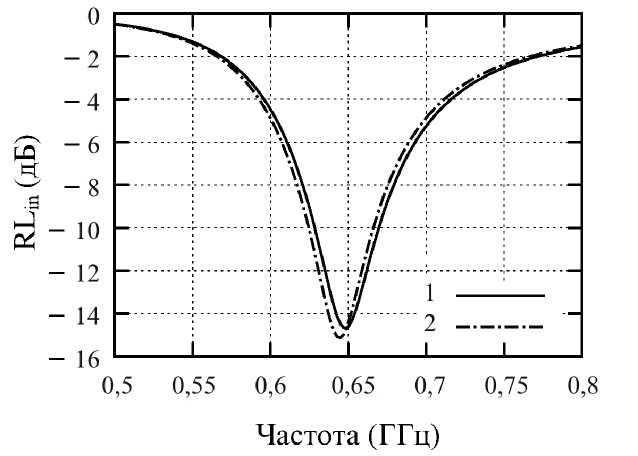
Рис. 4. Результаты расчета RL _in для ячейки размером 5,12 мм:

1 – метод, предложенный Railton и др.; 2 – метод, предложенный Taniguchi и др.

Fig. 4. The calculation results of the RL in for the cell with the size equal to 5.12 mm:

1 – the method proposed by Railton et al.; 2 – the method proposed by Taniguchi et al.

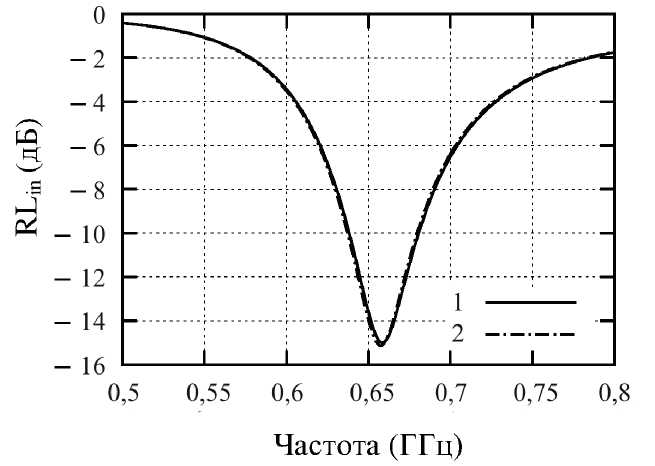
Рис. 5. Результаты расчета RL _in для ячейки размером 2,593 мм:

1 – метод, предложенный Railton и др.; 2 – метод, предложенный Taniguchi и др. Fig. 5. The calculation results of the RL in for the cell with the size equal to 2.593 mm: 1 – the method proposed by Railton et al.; 2 – the method proposed by Taniguchi et al.

Из рисунков видно, что корректировка магнитного поля вокруг источника заметно повлияла на результаты расчетов при крупном размере ячейки. При уменьшении размера ячейки данное влияние существенно уменьшается. При сравнении результатов на рис. 3 с более точными результатами на рис. 5

(за счет меньшего размера ячейки сетки) можно отметить, что в отличие от [8] корректировка магнитного поля вокруг источника существенно не увеличила точность расчетов (нельзя исключить однако, что этот вывод может зависеть от рассчитываемого параметра антенны). Наличие корректировки магнитного поля на концах проводников, не присоединенных к источнику тока, не повлияло на результаты расчетов.

Вычислительная неустойчивость

Следует отметить, что отсутствие корректировки магнитного поля вокруг источника может приводить к вычислительной неустойчивости. Ниже представлены расчеты интеграла напряженности магнитного поля вдоль контура вокруг источника (что равно полному току через поверхность, ограниченную данным контуром).

В первом примере проведены расчеты с небольшим значением коэффициента S . Использована прежняя модель, но с диаметром проводников 0,5·10 ^–3 мм. Проводники моделировались при помощи метода [2]. Параметры функции (8): n = 10, T = 10 ^–6 , τ = 3·10 ^–7 , η = 1. В качестве источника использовался идеальный источник тока. Размер ячейки – 10 мм, коэффициент S – 0,294. Конечно, данные параметры импульса и диаметр нереалистичны для антенны длиной 0,21 м, но они применяются лишь для демонстрации вычислительной неустойчивости при использовании модели, близкой к той, что была использована в предыдущих расчетах. Результат расчета без корректировки магнитного поля представлен на рис. 6. Из рисунка видно, что результаты расчета ошибочны.

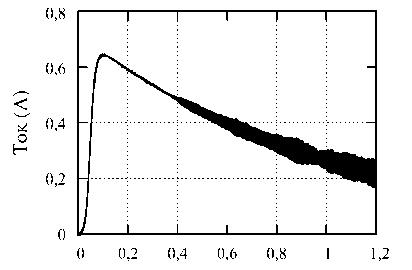
Время (мкс)

Рис. 6. Результат расчета тока без корректировки магнитного поля вокруг источника тока Fig. 6. Result of the current calculation. The magnetic field around the source is not corrected

Далее проведен расчет с применением корректировки компонентов магнитного поля. Корректируемые компоненты магнитного поля показаны на рис. 2. Результаты представлены на рис. 7. Можно видеть, что такой большой ошибки, как в предыдущем случае, нет. Причем поскольку проводники в данных двух случаях моделировались при помощи метода [2], продольные по отношению к проводнику компоненты магнитного поля не корректировались. Так как явная вычислительная неустойчивость устранена (корректировкой компонентов магнитного поля вокруг промежутка между проводниками), то можно предположить, что причина неустойчивости на рис. 3 отличается от причины неустойчивости, описанной в [3].

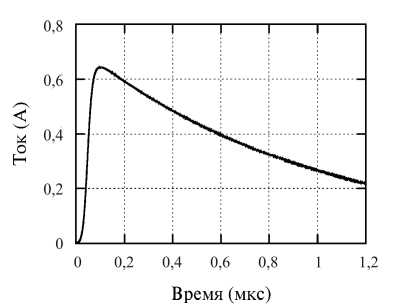
Рис. 7. Результат расчета тока с корректировкой магнитного поля вокруг источника тока Fig. 7. Result of the current calculation. The magnetic field around the source is corrected

В следующем примере неустойчивость возникает в самом начале расчетов. В данном случае проводники моделировались при помощи метода [3]. Параметры функции тока те же, что и в предыдущем случае: диаметр проводников – 0,5 мм; размер ячейки – 10 мм; коэффициент S – 0,98. В результате на рис. 8

видна явная ошибка. Конечно, устранения этой ошибки можно было бы добиться путем уменьшения значения коэффициента S , но это привело бы к увеличению времени расчета (пропорционально тому, во сколько раз уменьшено значение S ). Из результата расчета с применением корректировки магнитного поля на рис. 9 можно видеть, что вычислительная неустойчивость отсутствует.

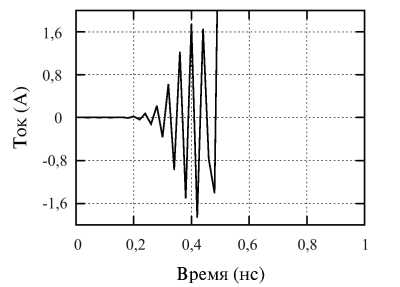
Рис. 8. Результат расчета тока без корректировки магнитного поля вокруг источника тока Fig. 8. Result of the current calculation. The magnetic field around the source is not corrected

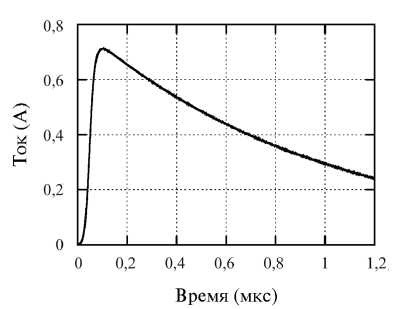
Рис. 9. Результат расчета тока с корректировкой магнитного поля вокруг источника тока Fig. 9. Result of the current calculation. The magnetic field around the source is corrected

Также проведены расчеты для случая, когда диаметры двух проводников, разделенных промежутком, различны. Расчеты выполнены на прежней модели, но с разными диаметрами двух проводников – 2 мм и 0,008 мм. Проведено два расчета, в которых магнитное поле корректировалось в соответствии с одним из проводников. Результаты (рис. 10) демонстрируют отсутствие вычислительной неустойчивости в обоих случаях: если магнитное поле вокруг источника корректируется в соответствии 1) с проводником большего диаметра и 2) с проводником меньшего диаметра.

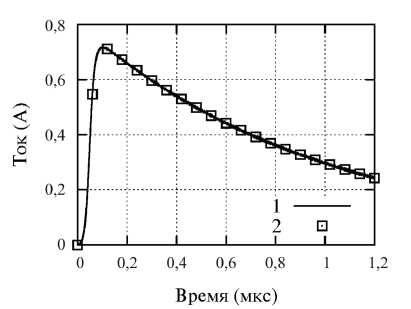
Рис. 10. Результат расчета тока с корректировкой магнитного поля вокруг источника тока (и проводниками разного диаметра): 1 – магнитное поле корректируется в соответствии с проводником диаметром 2 мм; 2 – в соответствии с проводником диаметром 0,008 мм Fig. 10. Result of the current calculation for the wires with a different diameter:

1 – the magnetic field around the source is corrected according to the wire with the 2 mm diameter; 2 – according to the wire with the 0.008 mm diameter

Корректировать магнитное поле следует и в тех случаях, когда в промежутке между проводниками нет источника, например, когда рассчитывается разность потенциалов между проводниками.

Стоит отметить, что после многочисленных расчетов с проводниками рассмотренная вычислительная неустойчивость была выявлена только в случаях, когда проводники расположены на расстоянии, равном одной ячейке. Возможно, что в корректировке магнитного поля на концах проводников в остальных случаях нет необходимости, либо такие случаи редки.

Заключение

Для устранения вычислительной неустойчивости при расположении проводников на расстоянии, равном одной ячейке расчетной сетки, вокруг разделяющего проводники промежутка необходимо корректировать магнитное поле точно так же, как и вокруг проводников. При этом нет необходимости корректировать магнитное поле на расстоянии ∆/2 от концов проводника во всех случаях, когда радиус проводника меньше значения 0,208·∆, как это предложено в [3].

Данную корректировку следует применять также и при использовании метода [2], т. е. если продольные по отношению к проводнику компоненты магнитного поля не скорректированы.

Применение этой корректировки не только устраняет вычислительную неустойчивость, но и влияет на результаты расчетов в целом (что не приводит к существенному повышению точности в случае расчета возвратных потерь). Поэтому корректировку предлагается использовать преимущественно для устранения неустойчивости.