Оценка погрешности и ее обоснование с помощью фильтрации численных результатов, полученных при разных числах узловых точек сетки

Тогда можно записать систему равенств zn 1 = z + ci п k1 + c 2 Ui k2 + .. + ClUi kL + A( ni)

, zn2 = z + cin 2 ki + c 2 n 2 k2 + ... + ClU 2 kL + A(n 2) , zn = z + Cin I ki + c2n ^ k2 + ... + ClUj kL +A(Ui )

Численной фильтрацией [1, 2] называется последовательное подавление (исключение) компонент погрешности, т.е. определение отфильтрованных последовательностей z(j), j=1,2,^ (j' - порядко-ni вый номер фильтрации). Для равенств (2) фильтрация сводится к линейной комбинации z(j) = a jz(j i) + P jz(j ?), причем a j и P j опреде-ni            ni              ni -i ляются из решения системы двух уравнений

—k       — k aj +pj = i ajni—ij +вjni j = 0 ,                                                                        .

Отсюда получаем формулу фильтрации, которая для модели процесса (1) совпадает с экстраполяционной формулой Ричардсона

_T ( j — i) __z( j — i) _z ( j ) = _z ( j — i) ₊ ni n i — i n i     n          Q^b- — i

,

n

Q = —— = const ⁿi — i

,

_c( j ) _{= c}( j —i) Q k j ^{— Q}k m ^cm   ^cm       k

^{Q 1 — i} , m=j +1,_, L . (3)

В результате фильтрации получается новая последовательность, не содержащая компоненты

• — k i

n ^j , которая в связи с сохранением вида остальных компонент при условии n = Qn i _— । может быть подвергнута повторной фильтрации для подавления следующей компоненты.

Оценки погрешностей получались в виде разности вычисленных и отфильтрованных резуль- татов

Д = |^

с   выбранным   значением эталона

—

zet . Отношение оценок последовательных фильтраций называется относительной размытостью оценки погрешности и позволяет определить, с какой точностью получена оценка. Поэтому результаты последней фильтрации используются только для подтверждения результатов предыдущей. Для обнаружения возможных ошибок в программе и других ненаблюдаемых погрешностей проводилось сравнение с приближенным решением, полученным независимо другим численным методом (проверке факта пересечения интервалов неопределенности). В [3] получена теоретическая оценка достоверности (доверительной вероятности) совместного результата решения этих задач. В качестве примера рассматривается задача об уединенной волне (солитоне) Стокса.

Постановка задачи.

Пусть струя идеальной жидкости движется вдоль горизонтальной прямолинейной стенки ADC (рис. 1 а ). Cила тяжести действует вертикально вниз. Рассматривается решение типа уединенной волны наибольшей амплитуды, при этом на вершине волны образуется излом с внутренним углом 2п/3 (волна Стокса). В точке B скорость жидкости равна нулю. Скорость на бесконечности - V » , асимптотическая толщина струи – h . Давление P на свободной границе равно атмосферному P 0 .

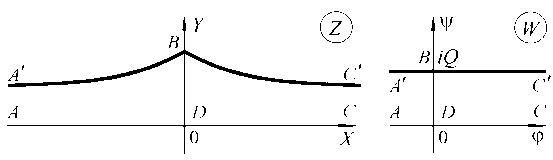
б

а

Рис. 1. Формы области, соответствующей течению, на плоскостях: а - физической Z = X + iY ;

б – комплексного потенциала

На свободной поверхности А'BC' значение модуля вектора скорости течения V связано с высотой точки Y уравнением Бернулли при P = P 0

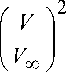
2 Y

Fr ² h

= const

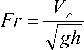
. (4)

где g – ускорение свободного падения; Fr – число

Фруда.

Для решения задачи применяются методы теории функций комплексного переменного [4]. В качестве области изменения параметрического переменного удобно выбрать полосу x = c + i u ширины 1 (рис. 2а). Поскольку границами течения являются линии тока, областью, соответствующей потоку на плоскости W также является полоса (рис. 1, б ). Поэтому зависимость W ( % ) определяется формулой

W (х) = Ф + i V = Qw (х) = — Q (% — i),   (5)

где ф , v - потенциал и функция тока течения;

Q = hV « - расход жидкости в струе.

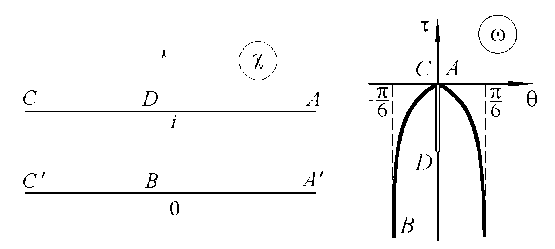
б

а

Рис. 2. Формы областей, соответствующих течению на плоскостях: а – параметрического переменного х ; б - логарифмического годографа скорости

Эта задача решалась многими исследователями [1, 2, 5-13] в течение ряда лет. В табл. 1 представлены численные результаты, полученные разными авторами, по числу Фруда для солитона Стокса. Число Фруда позволяет сравнивать условия волнообразования для разных глубин. В скобках после чисел указаны погрешности в единицах последнего приведенного разряда там, где погрешность превышает эту единицу. Следует отметить, что в цитируемых работах авторы, как правило, декларируют оценку погрешности на уровне единицы последнего приведенного разряда. Сравнение разных результатов показывает, что авторы часто ошибаются в оценке погрешности, причем иногда ошибаются в 10 и более раз. Применение фильтрации позволяет избежать таких ошибок.

Таблица 1. Значения числа Фруда, полученные разными авторами

Fr =1.286        (5)	Longuet-Higgins M.S., Fenton J.D. Proc. R. S. London. 1974. [5]
Fr =1.2909	Fox M.J.H. Ph.D. thesis. Cambridge univ. 1977. [6]
Fr =1.290906    (15)	Hunter J.K., Vanden-Broek J.-M. J.F.M. 1983. [7]
Fr =1.290889     (1)	Williams J.M. Phil. Trans. Roy. Soc. London. 1981. [8]
Fr =1.29089053   (7)	Evans W.A.B., Ford M.J. Proc. R. Soc. London 1996. [9]
Fr =1.290890455	Шерыхалина Н.М. ВИНИТИ. №2550-В95-деп. 1995 [10]
Fr =1.2908904558	Maklakov D.V. Euro. Journ. of Applied Mathematics. V. 13, 2002. [11]
Fr =1.29089045586	Житников В.П., Шерыхалина Н.М. Физика волновых процессов, № 23, 1998. [12]
Fr =1.2908904558634	Sherykhalina N.M., Zhitnikov V.P. Computational Fluid Dynamics Journ. V. 10, N 3, 2001. [13]
Fr =1.29089045586335	Житников В.П., Шерыхалина Н.М. Уфа: Гилем. 2009. [1]
Fr =1.290890455863341	Zhitnikov V.P., Sherykhalina N.M., Sokolova A.A. Mediterranean Journ. of Soc. Sci. 2015. [2]

Цель работы: подтверждение последнего полученного числа за счет повышения точности решения.

Метод решения задачи. Пусть Z = X+ iY , z = Z/h . Решение удобнее получать, если использовать плоскость логарифмического годографа скорости (функции Жуковского, рис. 2б)

e

3 т

dт dо

^-sin 0 = 0

Fr ²

Для выделения особенности в точке х = 0 определим функцию

f ⁽х )

i - e "

to = i ln — = 0 + i т dz

( i + ie    ² ) 2

где 0 - угол наклона вектора скорости жидкости к оси абсцисс т =1п( У / V 0.

Функция to ( х ) должна удовлетворять следующим условиям:

• 1)    при Re х =0, 0 < Im х < 1 действительная часть Re ю ( х ) = 0 = 0;

• 2)    при Im х = 1 действительная часть Re to ( х ) = 0 ;

• 3)    при Im x =0 действительная и мнимая части to ( х ) связаны уравнением (1);

• 4)    при х = о + i 0, о ^ ± 0 действительная часть Re to ( х ) ^ ± п/6;

• 5)    при х ^ ” величина ю ( х ) ^ 0.

Задача решается видоизмененным методом Леви-Чивиты [14]. Представим со ( х ) в виде суммы

которая имеет действительные положительные значения при х = о + i и при х = 0 + i и (0 < и <  i), стремится к 1 при Re х^ + » , стремится к 0 при х> 0.

Функцию to 2 ( х ) представим в виде:

^to 2 Ш 3 In f ⁽х^{) +} iC if f ⁽х^{))в - i ]}

Тогда

^{d to} 2 Ш d х

п

—

ch пх

п + i —

X

+ i в C i

i - e

.-пх

х р- i

.

3 sh пх

+

V

( i + ie ^-

п e

-

^п х/^{2 e}

, ^-п х/2

+ i

(i + ie "пх/2

.

При х = о + i 0

to(Z) = toi(Z) + to2 Ш,           (7)

to 2 ( о + i 0 ) = | arctg e

,-п° 2

+

i _ln

i - e

,-по

i + e

-по

+

где to 2( х ) - функция, удовлетворяющая условиям 1, 2, 4, 5.

В результате такого представления to _i ( х ) ^ 0 + i т 1 ( 0 ) при х > 0, т.е. функция to i ( х ) является непрерывной на границе. Функция to 1( х ) получается следующим образом. Будем искать на границе х = о в узловых точках о m ( m =0,..., n ) значения Re to i ( о _m ) = 0 _m . В силу предыдущего замечания 0 _О ( 0 ) = 0 . Кроме того, положим 0 _n ( о _n ) = 0, поскольку функция 0 ( о ) экспоненциально убывает при о ^ ». В промежуточных между узлами точках функция Re to i ( о ) получается с помощью интерполяции узловых значений 0 _m ( о _m ) кубическим сплайном, дважды непрерывно дифференцируемым. Для восстановления функции to i ( х ) используем формулу Шварца [1]

При

^{+ C} i

r

+ iC_i

-по i - e

V

i + e

i - e

-по

по

V

i + e

по

I sin ( 2в arctg

I cos ( 2в arctg

e

e

= 02 (о)+ i т2 (о)

,-по/ 2 )+

по/ 2 ) -

iC_i =

.

х = о + i 0, о ^ 0 + 0 для 0.5 < в <  i имеют

место оценки: f ( о + i 0 ) = ^ + O ( о ² ) ,

⁰ 2 ^{( о )} = ^п

—

по _ . I — + C i sm l

.

e

. 3т 2 ( о)_п_ ^п£      W^

sn

6 i 2 V 2

—

. в

i, по + -ln —

—

”

to i ( х ) = 0 1 ( х ) + Т 1 ( х ) = - i J Re to i ( о) —-------- — d о 0         ch по- ch пх

■ ^пв iC + iC cos — 11 2

,

.

d 0i п „ . пв Гпо —² = C i — в sin— — d о ⁱ 2 2 V 2

в- i

—

^п + O

■ (о^в )

,

При х ^ о _m + i 0, согласно формуле Сохоцко-го [4], получается главное значение (v.p.) интеграла

d т₂    i п_п пв

—² = — + C i —в cos—

3о    i 2      2

d о

.

<х> to1(оm Ii • v.p. J Re toi (о)

sh по ch по - ch по _m

d о + Re to i ( о _m )

Численное интегрирование производится по двухточечной квадратурной формуле Гаусса 4-го порядка точности. Представим краевое условие (4) в дифференциальной форме

Отметим также, что вследствие того, что 0 -нечетная, т - четная по о функции, значения 0 i ( 0 ) = 0, d ^ ^ ( 0 ) = 0. При подстановке этих соотно- d о

шений в (8) получим уравнение

п + С , П ( 1 +e ) cos^ 6    ¹2            2

= e

пст --+

3 ^С , - 3 . ,( 0 ) _^ Г1+³ ( d e , _{( 0 )а} Fr 2 2   2 ( d ст

+ С , sin

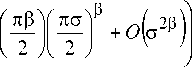
При приравнивании членов порядка O (1) и

O ( ст^в ) получаются следующие уравнения

• С , -t i ( 0 ) = - W 3^ 1

23 ^.

3 <п Fr² ;

,

(1+p)ctg     -1

В последнем уравнении определяется наименьший положительный корень. Форма свободной поверхности определяется с помощью численного интегрирования выражения

— = dz = dx + idy = e ^m dw = - e i “ ^{( x )} d x h

.

Для численного интегрирования применялась формула средних прямоугольников с последующей фильтрацией до достижения погрешности порядка 10-18.

Численное решение, обработка и анализ результатов. Численно задача решалась методом коллокаций. Уравнение (8) удовлет воряло сь в отдельных точках Х = ст m + i 0 ( m = 0, n - 1). Искомыми являлись значения Fr , С , , 6 _m , m = 1, n - 2. Полученная система n нелинейных уравнений решалась методом Ньютона с регулированием шага. Поиск решения прекращался, когда невязки по модулю не превышали 10^-20. Для решения использовались числа с длиной мантиссы около 35 десятичных разрядов. Отличительной особенностью данного метода является использование при численном решении условия (8) вместо (4), что позволяет избежать численного интегрирования при формировании системы уравнений. Это существенно ускоряет решение системы. Решение задачи о солитоне Стокса позволяет определить значения параметров волны, таких как число Фруда, амплитуда волны a = у в -, = Fr 2 2 и т.д. В работе [13] была декларирована точность полученного значения числа Фруда порядка 13-ти разрядов. Позже в [1] был применен другой метод фильтрации, и точность доведена до 14-ти десятичных цифр. В [2] были применены другие методы вычисления и фильтрации, погрешность была декларирована на уровне 2 единиц 15-го разряда. Результаты последующих расчетов подтверждали оценки, полученные в предыдущих с помощью фильтрации (см. табл. 1).

На рис. 3а, 3б представлены результаты фильтрации данных, полученных этими методами решения задачи. Результаты представлены в логарифмическом масштабе. По оси ординат отложены десятичные логарифмы оценок относительных погрешностей - lg5, 6 = |AFr/Fr| (точность полученных данных). Цифрой 0 отмечены оценки точности вычисленных данных, цифрами 1, 2. … – результаты первой, второй и т. д. фильтрации. Видно, что с помощью фильтрации удалось подавить несколько регулярных компонент (1) и на два порядка и более уменьшить погрешность искомого параметра Fr.

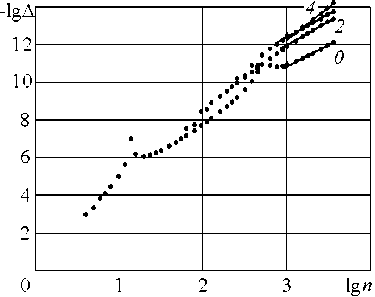
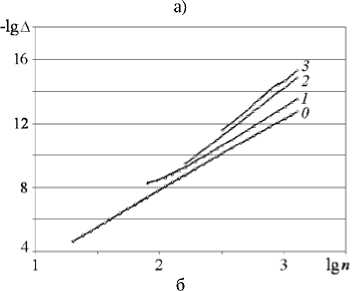
Рис. 3. Результаты фильтрации числа Фруда: а) согласно [13]; б) согласно [2]

Для проверки оценок, полученных ранее, было необходимо применить другой метод и получить независимые результаты. Для этого и был разработан метод, изложенный в данной работе. Результаты использования предложенного метода и расширенной мантиссы показаны на рис. 4. В качестве формулы фильтрации применялась комбинация формул Эйткена [1] и Ричардсона (3). Видно, что с помощью фильтрации (исключения основной компоненты (1) четвертого порядка) точность порядка 16 значащих цифр может быть достигнута при n =5120. Результаты второй фильтрации (линия 2 ) используется только для подтверждения полученной оценки [2].

Сравнение со значением, полученным в [2], показало отличие около - 1,5 - 10 '5 . Тем самым, оценка, полученная ранее в [2], была подтверждена, и получено новое значение числа Фруда, равное Fr =1,2908904558633395 ± 10-¹⁶. Кроме того, была модифицирована программная реализация используемого численного метода, что позволило значительно увеличить скорость вычисления.

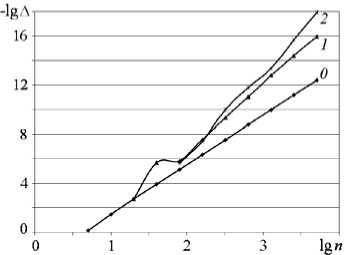
Рис. 4. Результаты фильтрации числа Фруда

Выводы: фильтрация, выполняемая на этапе постпроцессорной обработки данных численного эксперимента, дает возможность получить достоверные оценки погрешности и существенно повысить эффективность численных алгоритмов. Тестирование с помощью сравнения с точными или приближенными (полученными другими способами) частными решениями позволяет подтвердить или опровергнуть эти оценки. Был разработан метод решения задачи о солитоне Стокса, позволяющий ускорить процесс вычисления данных. В работе показано, что оценкам, полученным ранее с помощью фильтрации, можно доверять, и подтверждено получение точности вычисленного ранее другим методом числа Фруда около двух единиц 15-го разряда.

Работа выполнена при финансовой поддержке Минобрнауки России в рамках базовой части госзадания образовательным организациям высшего образования. Код программы 2229.