Оценка погрешности измерения геометрических параметров объектов при проектировании стереоскопических систем

Стереоскопический метод измерения трехмерных координат объектов широко используется для решения различных задач технического зрения, в медицине, биологии и других областях. Данный метод является бесконтактным, пассивным, позволяет проводить измерения во всех точках изображения и создавать текстурированные трехмерные (3D) модели объектов. Для реализации метода требуется система регистрации, позволяющая получить изображения объекта с двух и более ракурсов. Калибровка такой системы и определение соответствующих точек на изображениях позволяют вычислять трехмерные координаты точек объекта и производить геометрические измерения его параметров в соответствии со схемой, показанной на рис. 1 [1]. Алгоритм вычисления трехмерных координат использует математическую модель формирования изображения (ММФИ), параметры которой определяются при помощи алгоритма калибровки. Такая модель содержит минимум информации о системе регистрации изображений, необходимый для вычисления 3D-координат точки по ее двумерным (2D) проекциям на изображениях. Эта информация также может использоваться для ограничения области поиска или дополнительной обработки изображений (устранения дисторсии, ректификации) при поиске соответствующих точек. Это показано пунктиром на рис. 1.

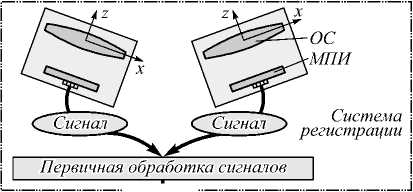
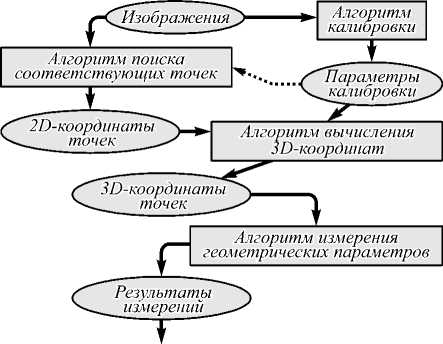
Рис. 1. Основные этапы обработки данных при использовании стереоскопического метода

Известны различные схемы регистрации изображения объекта с нескольких ракурсов: с отдельными оптическими системами (ОС) и матричными приемниками излучения (МПИ), с перемещением одной ОС и МПИ, а также сложные ОС, позволяющие регистрировать изображения с разных ракурсов на одном МПИ поочередно [2, 3] или одновременно за счет использования призм [4–7], зеркал [8, 9] или дифракционных решеток [10]. В зависимости от типа ОС для их описания используются различные ММФИ [4–7, 11], которые часто в явном виде содержат конструктивные параметры ОС, МПИ или отдельных элементов (фокусное расстояние, координаты центра входного зрачка, показатель преломления материала призмы, размер пикселя и др.).

При проектировании измерительных стереоскопических систем критерий качества формируется исходя из величины погрешности измерения трехмерных координат и геометрических параметров объекта. Основные источники погрешности и ее преобразования на различных этапах обработки данных показаны на рис. 2. При этом на свойства зарегистрированных изображений (пространственное разрешение, отношение сигнал/шум, дисторсия) влияет множество факторов, из которых только малая часть представлена в ММФИ, что не дает возможности анализировать их, не вводя более подробных математических моделей. С другой стороны, ММФИ достаточно для расчета преобразования погрешности в пределах выделенной на рис. 2 зоны, что позволяет использовать ее для предварительных расчетов на начальном этапе проектирования и для формулировки основных требований к ОС и МПИ на последующих этапах [12].

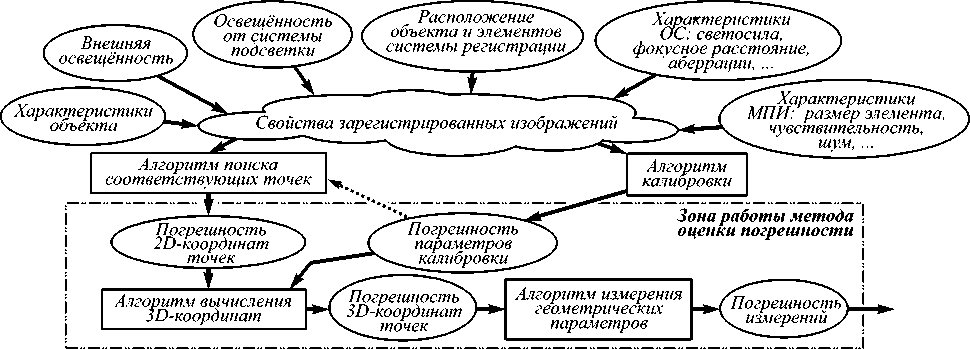
Рис. 2. Основные источники погрешности измерения геометрических параметров объекта стереоскопическим методом

Таким образом, для расчетов необходимо иметь метод оценки погрешности, который позволяет вычислить ее при известных погрешности определения координат соответствующих точек на изображениях и погрешности параметров калибровки (входные данные метода). Выбор вида представления погрешности (доверительный интервал, среднеквадратическое отклонение (СКО) или др.) зависит от метода. Чтобы на этапе проектирования иметь возможность сравнения различных типов ОС, данный метод должен быть достаточно универсальным относительно ММФИ. Наличие такого метода также необходимо в процессе эксплуатации, например, для выдачи рекомендаций оператору и принятия решений о корректности результатов контроля.

В настоящее время разработано несколько методов для оценки погрешности, которые могут быть применены для решения данной задачи. Одним из них является метод интервальных оценок, основанный на задании значений погрешности в виде доверительных интервалов [13]. Его недостатками являются завышенные результирующие значения погрешности и сложность применения к преобразованиям, заданным в неявном виде. Метод применялся для оценки погрешности 3D-координат, полученных стереоскопическим методом при использовании проективной модели [14], а также для оценки погрешности в задачах определения положения и ориентации робота по измеренным 3D-координатам объектов [15, 16]. Использование метода для произвольной ММФИ затруднительно.

Другую группу составляют методы, в которых погрешность характеризуется параметрами плотности распределения вероятностей. Так, в работах [17, 18] распределение вероятностей для 3D-координат точки было рассчитано аналитически при использовании упрощенной проективной модели. В случае, когда ММФИ и алгоритм вычисления 3D-координат описываются нелинейными преобразованиями или преобразованиями, заданными в неявном виде, обычно используется линеаризация. Такой подход чаще других применяют для оценки погрешности 3D-координат, полученных стереоскопическим методом [5, 12, 19–21]. При этом обычно принимают допущение о нормальном законе распределения (НЗР) входных данных и для описания используются их средние значения и матрицы ковариации. Однако данный метод не позволяет оценить смещение оценки и может приводить к значительным ошибкам, которые зависят от вида нелинейного преобразования.

Подходом, альтернативным линеаризации нелинейных преобразований, является использование сигма-точечного преобразования (unscented transfor- mation, далее – UT-метод) [22, 23]. В данном методе погрешность задается средним значением и матрицей ковариации; при расчете нелинейное преобразование применяется к специальным образом сформированной выборке из входных данных. Чаще всего применяется для модификации фильтра Калмана (Unscented Kalman filter) при прослеживании положения и скорости движения объекта. Достоверность получаемых оценок зависит от выбора внутренних параметров метода [24–26]. Метод пригоден для любых ММФИ и алгоритмов вычисления 3D-координат, поскольку рассматривает их как «черный ящик», позволяет оценить смещение оценки и уже использовался для расчета погрешности измерения геометрических параметров призменно-линзовой стереоскопической системой [27, 28]. По сравнению с методом, в котором используется линеаризация нелинейных преобразований, UT-метод обеспечивает большую точность оценки для проективной ММФИ [29].

Самым надежным и универсальным методом оценки погрешности является моделирование на основе метода Монте–Карло, однако его использование при оптимизации параметров системы или оценке различных вариантов на стадии проектирования невозможно из-за высокой вычислительной сложности.

Приведенные в литературе результаты исследований эффективности перечисленных выше методов в основном касаются только проективной ММФИ и не позволяют сделать однозначного вывода о преимуществе одного из них.

Целью исследований, изложенных в статье, является обоснование метода оценки погрешностей стереоскопических систем, предназначенных для измерения трехмерных координат и геометрических параметров объектов. Для достижения этой цели проведён сравнительный анализ метода линеаризации, метода интервальных оценок и UT-метода применительно к таким системам. В данной работе эти методы сравниваются с результатами моделирования Монте–Карло для проективной (на примере типовой системы регистрации из двух камер) и трассировочной (на примере эндоскопической призменно-линзовой ОС) ММФИ.

li= Ег (lw) = (cLvT)T при ci = Ricw+ ti , vi = Rivw. Преобразование Pi определяет соответствие pi = Pi(li) между лучом li в пространстве предметов i-й камеры и точкой pi в ее плоскости изображения. Знак «◦» используется для последовательного применения преобразований, то есть Pi ° Ei(lwi) = Pi(Ei(lwi)). Набор преобразований Ei и Pi описывается вектором параметров k, который определяется в результате калибровки. Аналогично можно записать обратное преобразование lw i = Ei"1 °P"1 (Pi), позволяющее найти луч lwi в ГСК для каждой точки pi в плоскости изображения. ММФИ можно разделить на две большие группы в зависимости от того, прямое или обратное преобразование записано для них в явном виде.

Проективная модель. Наиболее широко в компьютерном зрении используется центральная проективная (pinhole) модель [1, 11, 20, 31]. Она подразумевает, что все лучи l i для i -й камеры проходят через центральную точку (центр проекции):

T l, = ((0,0,0)T , vt) .

Следовательно, можно использовать одну точку x i для задания каждого луча и заменить l i на x i и l w i на x w в

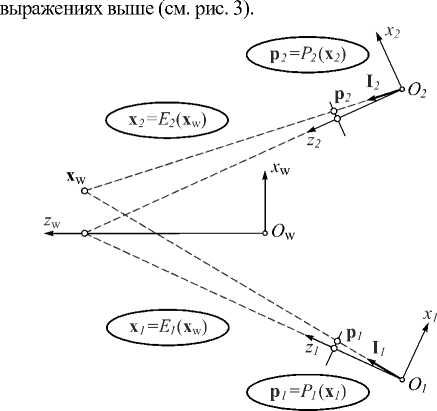
Рис. 3. Центральная проективная ММФИ

Обычно в такую модель дополнительно включают дисторсию ОС, тогда преобразование P i записывают в виде комбинации простых преобразований [30]

p i = P i ° E i ( x w ) = A i ° D i ° F ° E i ( x w ) , (1)

где F – центральная проекция на единичную плоскость xi = F (xi); Di - 2П-преобразование дисторсии xi = Di (xi) и Ai - 2D аффинное преобразование p i = Ai (x"). В зависимости от типа ОС преобразование дисторсии Di представляется в виде полиномиальных или более сложных моделей [1, 11, 30, 31]. Чисто проективная модель (не включающая преобразование Di) поз- воляет записать и прямое, и обратное преобразование в явном виде. Полиномиальные модели дисторсии не всегда имеют явное выражение для обратного преобразования D–1, вместо него используется итерационная процедура [11, 30]. В этом случае проективная ММФИ с дисторсией относится к первой группе.

Трассировочная модель. Вторая группа ММФИ включает трассировочные модели, в которых луч l w i в ГСК определяется путем задания точек пересечения луча с двумя плоскостями [11], в том числе при помощи полиномов [32] или при помощи трассировки от плоскости изображения через стеклянную пластину [3] или призму [4, 6, 7]. Как правило, такие ММФИ являются нецентральными и вычисление прямого преобразования для них требует итерационного метода (ray aiming), так как направляющий вектор луча l w i для произвольной точки x w заранее неизвестен.

В данной работе в качестве примера используем ММФИ для системы, регистрирующей два изображения на одном МПИ за счет применения призмы [4, 6, 7]. Для описания трассировки лучей введем обозначение для преобразования луча l k , i = S k, i ( l k –1, i ) при его преломлении на k -й поверхности для i -й части изображения согласно закону преломления в векторном виде (рис. 4).

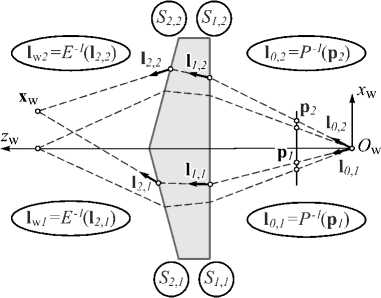
Рис. 4. Трассировочная ММФИ для призменно-линзовой системы

Для определения координат луча l0, i используется обратная проективная модель, далее рассчитывается преломление луча на двух поверхностях призмы. Преобразование P –1 зависит только от параметров основной ОС и МПИ и является одинаковым для обеих частей изображения. Подобно выражению (1), обратное преобразование можно представить в виде последовательности преобразований l w i = E-1 о P-1 (p,.) = ii (2)

= E-1 о S2,i о Sy о F-1 о D-1 о A-1 (pi), где преобразование E одинаково для обеих частей изображения в соответствии с выбором СК [7]. На рис. 4 преобразование E показано как единичное. Преобразование D –1 здесь учитывает только радиальную дисторсию и записано в явном виде.

Алгоритм вычисления 3D-координат. Вычисление 3D-координат точки x w по N ее 2D-проекциям p i рассматривается как задача минимизации вида

Xw = argmin (C (xw, p, k)), (3) xw где p =(pf, pT,..., P N) , C — оценочная функция. Обозначим алгоритм вычисления 3D-координат (триангуляции) как алгоритм T, решающий данную задачу минимизации: Xw = T(p,k). Обычно в качестве такого алгоритма используются итерационные алгоритмы, такие как алгоритм Левенберга–Маркуардта [20]. Выбор оценочной функции C в общем случае не очевиден, поскольку он зависит от априорных данных о положении точки xw и ее проекций pi, статистики погрешности измерения координат проекций и свойств ММФИ. Для ММФИ первой группы, таких как центральная проективная ММФИ, лучшим выбором оценочной функции является расстояние Маха-ланобиса в плоскости изображения [20, 21]

C ( x w , p , k ) = ( p ^- p ) ^{T 2} - 1 ( p ^- p ) , (4) где p = ( p f , p T ,..., p N ) T , p i = P i о E i ( X w ) - оценка координат проекции точки x ˆ _w в плоскости изображений i -й камеры, а 2^{- 1} - обратная (или псевдообратная с учётом ранга) матрица ковариации ошибки измерения координат для p . Поскольку преобразования E i и P i зависят от k , p в формуле (4) является функцией p ( X w , k ) . Для ММФИ второй группы, не имеющих прямого преобразования в явном виде, целесообразно использовать оценочную функцию на основе расстояния d от точки x w до лучей l w i в ГСК:

d ² ( x w , l w i ) = b i^T b i ,

b i = (М з х з

v w i v w i^ ) ( c w i

^^^^^^B

где Id3x3 - единичная матрица размера 3x3. Введя обозначения d 2 (Xw, lw i) = biT bi, b = (bf, bT,..., bN)T и 1 w =(1 w 1^,1 w 2^

TT

¹ w N ) ,

запишем оценочную функцию аналогично (4):

C ( X w , p , k ) = b ^T s - 1 t >,                               (6)

где 2b - матрица ковариации для b, которую можно выразить через 2b на основе выражений (5) в виде db 51 w у 51 w T db T

2 b           2 p

5 1 _w d p d p d 1 _w

В соответствии с выражениями (2) и (5) b также является функцией b ( X _w, p , k ) . Для вычисления ∂ l w / ∂ p требуется продифференцировать выражение (2), для вычисления ∂ b / ∂ l w – выражения (5).

• 2.    Методы оценки погрешности

Допустим, что для принятой ММФИ с известным набором параметров k вектору 3D-координат x _w соответствует вектор координат точек в плоскостях изображений p = ( p ^ , p 2,.., p N ) . В случае измерения 3D-координат точки x ˆ_w постановку задачи для метода линеаризации и UT-метода можно определить в следующем виде: найти смещение оценки E [ x w - x w ] и апостериорную матрицу ковариации S x для вычисленного значения x ˆ _w при известном среднем значении E [ p - p ] = E [ p ] - p и матрице ковариации S p . Здесь и далее оператор E [ ] обозначает математическое ожидание.

Для оценки погрешности геометрических измерений в исходных данных должны присутствовать координаты всех точек, участвующих в рассматриваемом измерении (например, 2 точки для измерения длины отрезка, 3 точки для измерения площади треугольника, 4 точки для измерения расстояния от точки до плоскости и т. д.). Будем считать, что в рассматриваемом измерении участвует M точек, для каждой из которых определим вектор 3D-координат xwj и вектор проекций p j , j = 1...M, так, чтобы измеренное по этим координатам значение некоторого скалярного геометрического параметра r было равно его «истинному» значению r . В данном случае задачей метода будет определение смещения оценки E [Г" - r ] и СКО ar для вычисленного значения геометрического параметра rˆ при известных средних значениях E [pr - pr ] и общей матрице ковариации Sp r    для ошибки измерения вектора pr = (p1T, p2T,…,pM T)T координат всех точек.

Метод линеаризации. Чтобы использовать метод линеаризации, воспользуемся теоремой, приведенной в [19], для задачи минимизации (3). В случае использования ММФИ первого типа и оценочной функции (4) для измерения 3D-координат точки получим

E [xw - xw ^^xwE [p - p] = N-1 ^p- S-1E [p - p], Op sx -xw    dxw2 = N-1,(8)

dp dp J' _i dp где Np = — Sp17—, dxw для вычисления производных ∂p / ∂xw используется выражение (1). Если требуется учесть влияние погрешности параметров калибровки, разложим преобразования Pi ° Ei в ряд по степеням k в окрестности k и используем приближение первого порядка

, х d(Pi °Ei(xw )), pi - pi ® pi - P ° Ei (xw)---------- (k - k). (9)

dk

В случае, когда погрешности для p и k независимы, выражения (8) примут вид

E [ x w - x w ] ^x w E [ p - p ] + ^d x w E F k - k ] = d p            d k ^{L J}

= N p ^{- 1}

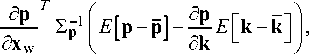
S = ^{d x} w s x d p

. dx w ^{2 p} d p

d x w d x w

+Sk dk k dk

= N p ^{- 1}

+ N - 1

AT S. |p Sk Ц2 S-2 |p-Np-2 dxw     dk dk     dxw где E |^k - k] = E [k] - k - среднее значение и Sk -матрица ковариации отклонений k от k . Вывод выражений для ∂p / ∂k зависит от принятой параметризации преобразований в выражении (1).

Для ММФИ второго типа и оценочной функции (6) указанная теорема применяется аналогично, в выражениях (8-10) нужно заменить p на b , S _p на S b и использовать E i ^{- 1} ° P ’^-1 вместо P i ° E i в выражении (9). Отметим, что для применения теоремы алгоритм T должен решать задачу минимизации типа (3).

Чтобы оценить погрешность измерения скалярного геометрического параметра r методом линеаризации, вначале определим смещения E[xw r - xw r] и матрицу ковариации Sxr ошибки измерения объединённого вектора трёхмерных координат xw r

1 T 2 T _w , x _w

M T x _w

T

для всех точек, участвующих в измерении. Для этого используем формулы (8 – 10), где заменим все вектора и матрицы на их объединённые для всех точек аналоги:

p на p r , x _w на

^x w r

1 T 2 T M T^T _w , x _w ,..., x _w ,

dp dx w dpr       (dp1 dp2

^на =diag ^diag l TT’TT d x w       I d x w d x w

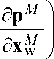
dp на dk

d p r d k

"dp12 dp2 2 dpM 2)2 dk , dk , , dk и т. д. Следует отметить, что при наличии погрешностей калибровки ошибки измерения 3D-координат отдельных точек xˆ wj могут быть зависимыми даже при независимых ошибках координат на изображении p j, т. е. Sxr *dlag(SX,S2,...,SM) при Spr = dlag(sp,Sp,...,SM).

Далее искомые значения смещения E [r - r ] и СКО ar вычисляются по формулам

E [ Г-r ]=^ E [ xwr dx w r dr       dr 2

a r = T Sx r “ dxw r    dxw r xw r

.

Как правило, значение измеряемого критерия r выражено через координаты x _w ^j в явном виде, так что выражения для частных производных ∂ r / ∂ x w r также можно найти в явном виде.

UT-метод. Основная идея метода состоит в том, что вместо упрощения нелинейного преобразования используется упрощение характеристик плотности распределения вероятности (ПРВ) исходных данных, по сути заключающееся в дискретизации ПРВ. Рассмотрим применение метода на примере измерения 3D-координат точки.

Вначале требуется задать набор из L векторов p 1 , l = 1... L и их весовых коэффициентов w m l и w c l (так называемых сигма-точек). Значения p i 1 и w _{m 1} , w c ₁ выбираются в соответствии с имеющейся информацией о статистике для p ; весовые коэффициенты должны удовлетворять условию нормировки ^ L = 1 w _m i = ^ L = 1 w c i = 1. В случае использования симметричной схемы [22, 29] для вектора p размерности m задаётся L =2 m + 1 точек:

P i = e [ p ], 1 = 1;

< p 1 = E [ p ] + (7 ( m + X ) X p ) ₁ _ 1 , 2 <  1 <  m + 1;

p 1 = E [ p ] - (^ ( m + X ) X _p ) 1 1 , m + 2 <  1 <  2 m + 1;

wm 1 = X/( m + X), 1 = 1;

” w c 1 = w m 1 + ( 1 -a ² + в ) , 1 = 1;                (12)

w _m 1 = w _c 1 = 1,2 ( m + X ) , 2 <  1 <  2 m + 1.

Здесь X = a2(m + к)-m; величины a, в и к являются параметрами. Под обозначением (,^(m + X)Xp ) подразумевается (l –1)-я строка квадратного корня из матрицы (m+X)Xp. Далее алгоритм T применяется к заданному набору векторов координат проекций p 1, чтобы полу чить набор векторов 3D-координат x w 1 = T (p 1, k). По этому набору вычисляются E [xw - xw ] и Xx:

L

^E [ x w ] = ^, ^w m 1 ^x w 1 , ^E [ x w ^— x w ] = ^E [ x w ] ^— x w ,

1 = 1

X x =]T w c 1 ( x w 1 — E [ X w ] )( x w 1 — E [ X w ] ) ^T .    (13)

1 = 1

Погрешность полученных оценок во многом зависит от метода выбора p i 1 и w _{m 1} , w _{c 1} , некоторые из которых обсуждены в [23], а также выбора параметров a , в и к [25]. Отметим, что UT-метод позволяет одинаково работать не только с ММФИ обоих типов, но и произвольным алгоритмом T , в том числе не использующим оптимальные оценочные функции и даже не обязательно решающим задачу вида (3).

Если требуется оценить влияние погрешности определения параметров калибровки, то во всех выражениях для UT-метода, приведённых выше, следует вместо век- тора p использовать объединённый вектор (pT, kT)T. Соответственно, в выражениях (12) вместо E[p] нужно использовать (E[p]T, E[k]T)T, а вместо Xp - diag(Xp, Sk). Полученный набор из L векторов (piT, kT) далее аналогично используется для определения

P 1 , k 1 ) .

В случае оценки погрешности измерения параметра r UT-методом каждый вектор координат p i r 1 в плоскости изображения будет включать координаты для всех точек, в выражениях (12) будут использованы E [ p _r] и X _{p r} соответственно. Для каждого p _r 1 последовательно применяется алгоритм T и вычисляется значение r (это преобразование целиком также можно рассматривать как «чёрный ящик»). Таким образом, выражения для параметра r примут вид

L

E [ r] = Z^ wm 1r, E [ r — r ] = E [ r1] — r, 1=1

L ₂

Xx =Z wc 1 (r — E [r*]) .

1 = 1

Если использовать выражения (13), то в таком случае будут вычислены E [ X _{w r} — x _{w r} ] и X _xr.

Метод интервальных оценок. В отличие от двух ранее рассмотренных методов, метод интервальных оценок описывает погрешность в виде доверительного интервала. Непосредственное применение этого метода к алгоритму T , для которого нет формулы в явном виде, затруднительно. Однако можно использовать метод линеаризации или UT-метод для алгоритма T , а метод интервальных оценок – для алгоритма вычисления геометрических параметров. Использование такого комбинированного метода оправдано тем, что по результатам измерения ПРВ большинства геометрических параметров может сильно отличаться от НЗР, в частности, быть значительно несимметричной, так что симметричные доверительные интервалы, построенные на основе E [ т^ — r ] и G _r, могут приводить к ошибочной оценке.

Для реализации предложенного подхода сначала необходимо рассчитать E [ X _{w r} — x _{w r} ] и X x _r методом линеаризации или UT-методом и на их основе задать границы интервалов ( x w _r, X w _r J . Одним из вариантов задания интервалов будет принять, что x ˆ _{w r} подчиняется НЗР и использовать квантиль распределения х ² для выбранной вероятности. Далее, применяя правила для преобразования интервалов к формуле для вычисления значения r , необходимо найти границы интервала ( r ^— , r ⁺J . В случае, когда матрица X x r не является диагональной, требуется применить соответствующее преобразование [13] и учесть его в формуле для вычисления r .

• 3.    Компьютерное моделирование

Чтобы оценить универсальность каждого метода, при проведении компьютерного моделирования были выбраны системы, использующие ММФИ двух разных типов.

В первом случае рассмотрена типичная система регистрации из двух камер, для описания которых используется проективная модель (1). МПИ каждой из камер имеет 1600×1200 элементов размером 6×6 мкм², фокусное расстояние объективов составляет 25 мм, угловое поле каждого канала – около 22°. Для описания дисторсии используется радиальная полиномиальная модель [31] с коэффициентом k 1 = 0,1. Расстояние между камерами составляет 200 мм, угол поворота одной камеры относительно другой – 0,1 рад. Рабочий диапазон расстояний системы – от 1000 до 3000 мм.

Во втором случае для примера взяты параметры трассировочной модели (2), полученные в результате калибровки промышленного эндоскопа Mentor Visual iQ VideoProbe производства GE Inspection Technologies с призменной стереонасадкой прямого обзора XLG3TM616060FG, обеспечивающей угловое поле каждого канала 55° ×55 ° [7]. Диаметр зонда равен 6,1 мм, рабочий диапазон расстояний – от 10 до 40 мм.

Для алгоритма измерения 3D-координат в первом случае использована оценочная функция (4), во втором – (6).

Измерение 3D-координат точки. Была проведена оценка погрешности измерения 3D-координат точки, расположенной в разных частях рабочего объема на разных расстояниях z. При этом матрица ковариации Σp r была задана в виде Σp r = σp2Id4×4, погрешности параметров калибровки не учитывались. Для UT-метода значения параметров были приняты α = 1, β =0 и κ = 4, для расчётов методом Монте – Карло использовались 105 значений. На рис. 5 показаны средние значения и сечения эллипсоидов ковариации в плоскости xOz, рассчитанные для вероятности 0,9545 для нескольких точек в центре и на краю рабочего объема. Для проективной модели точки взяты на расстоянии z = 2500 мм при σp = 1, для трассировочной модели – на расстоянии z = 30 мм при σp= 0,3. Результаты, полученные разными методами, практически совпадают и не различимы в масштабе рисунка. Смещение E[xˆw- xw] в обоих случаях мало и по модулю не превосходит 0,1% от расстояния z.

Для иллюстрации зависимости погрешности измерения 3D-координат точки от расстояния z и погрешности определения координат соответствующих точек σ p построим графики для СКО σ p погрешности вычисления координаты z точки x ˆ w (рис. 6).

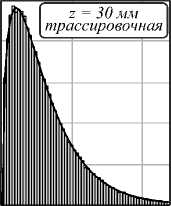
Результаты, полученные разными методами, очень близки, разница в значениях σ z не превышает 1%. Далее был проведен расчет расстояний Махаланобиса для x ˆ _w , полученных моделированием Монте–Карло, что показано на рис. 7 в виде гистограмм для точки на краю рабочего объема для обеих моделей.

Гистограммы хорошо соответствуют χ 2 распределению с 3 степенями свободы, что говорит о том, что распределение для x ˆ w близко к НЗР.

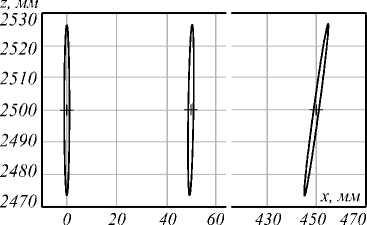
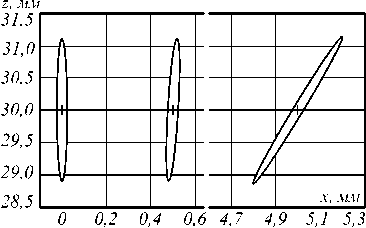
Рис. 5. Эллипсы ковариации, характеризующие погрешность измерения 3D-координат точки в плоскости xOz: для проективной (а), для трассировочной (б) модели

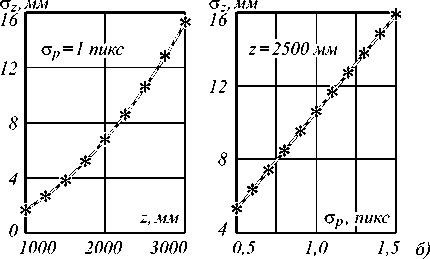
Рис. 6. Зависимость СКО погрешности измерения z-координаты точки от z-координаты и СКО погрешности определения координат соответствующих точек для проективной (а) и для трассировочной (б) модели

а)

Измерение длины отрезка. В качестве примера для измерения геометрических параметров проведе- ны оценки погрешности измерения длины для отрезка длиной r, расположенного в центре рабочего объ- ема на разных расстояниях z. Поскольку результаты для проективной и трассировочной моделей схожи между собой и приводят к одинаковым выводам, для экономии места далее приведены только расчеты для трассировочной модели.

Координаты точек отрезка заданы в ГСК: для х -отрезка x W = ( - r /2,0, z ) T , x W = ( r /2,0, z ) T ; для z -отрезка x W = ( 0,0, z - r /2 ) T , x W = ( 0,0, z + r /2 ) T .

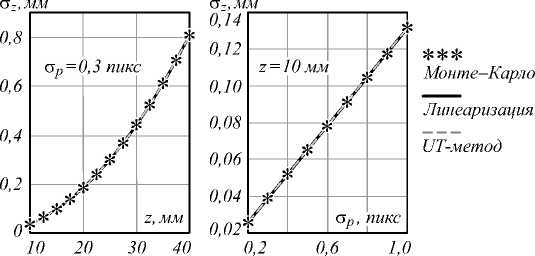
Матрица ковариации Spr была задана в виде 2p r = Op2 Id8x8 с ap = 0,3, остальные параметры взяты аналогично расчету для 3D-координат точки. При расчёте интервалов для вероятности 0,9545 методом Монте–Карло интервалы для вероятности (1 –0,9545) /2 были отсечены с обеих сторон. Для метода линеаризации и UT-метода применялась их комбинация с методом интервального анализа, как описано выше. Результаты оценки для отрезка длиной 1 мм показаны на рис. 8: верхний ряд графиков соответствует изме- рениям для x-отрезка, нижний – для z-отрезка; левый столбец графиков относится к методу линеаризации, правый – к UT-методу.

Очевидно, что границы интервала для вероятности 0,9545, полученные методом Монте–Карло, заметно отличаются от границ E [ r ] ± 2 a _r, то есть полученная ПРВ для r ˆ заметно несимметрична.

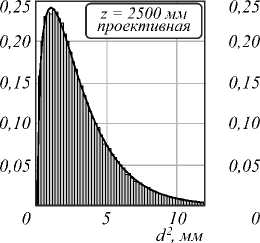
Рис. 7. Гистограммы расстояния Махаланобиса для измеренных 3D-координат точки и X —распределение

5       10

d² л/л/

Метод линеаризации                    UT-метод х-отрезок, мм                         х-отрезок, мм

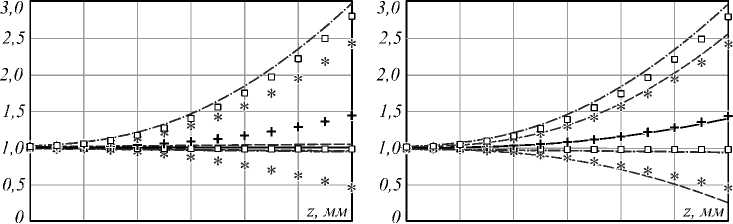
Моделирование Монте-Карло

+ + + среднее значение

£И

*** интервал £Й±2ог

□ □ □ интервал 0,9545

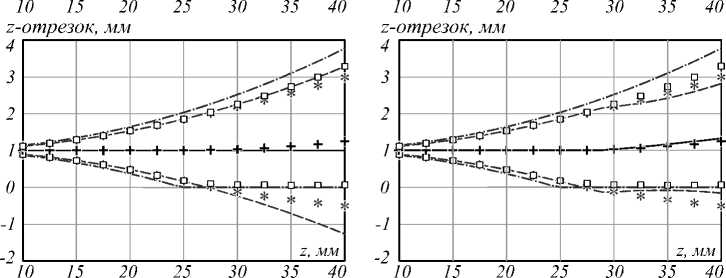
Оценка методом линеаризациии UT-методом среднее значение £И

интервал

ЕЙ±2а,- интервал 0,9545

Рис. 8. Оценки погрешности измерения длины отрезка в зависимости от z-координаты

Проанализируем гистограммы для r ˆ при двух значениях расстояния z = 10 мм и z = 30 мм (рис. 9 а для измерения x -отрезка и рис. 9 б для измерения z – отрезка соответственно). На рисунках дополнительно на врезке показано соотношение измеряемого отрезка r и эллипсоидов ковариации для погрешности измерения 3D-координат его концов. Для эллипсоидов также обозначен доверительный интервал A z измерения z -координаты при вероятности, равной 0,9545, для сравнения с истинной длиной отрезка.

Из гистограмм для x-отрезка видно, что ПРВ уже при малых z является несимметричной. E [rˆ] смещено относительно r = 1 мм, величина смещения увеличивается с увеличением расстояния z. Напротив, гистограммы для z-отрезка демонстрируют, что ПРВ приблизительно соответствует НЗР до тех пор, пока расстояние z не превышает 25 мм (при этом расстоянии доверительные интервалы Az для начала и конца отрезка начинают перекрываться).

Как видно на рис. 8, метод линеаризации даёт неправильное значение a r для x -отрезка, поскольку ПРВ для r ˆ уже при малых z заметно отличается от НЗР. UT-метод позволяет адекватно предсказать значения E [ r ] и a r во всех случаях, хотя может давать заниженные значения. На графиках для z -отрезков можно отметить, что при малых значениях z , когда ПРВ для r ˆ близко к НЗР, оба метода демонстрируют одинаковые результаты, совпадающие с результатами моделирования Монте–Карло.

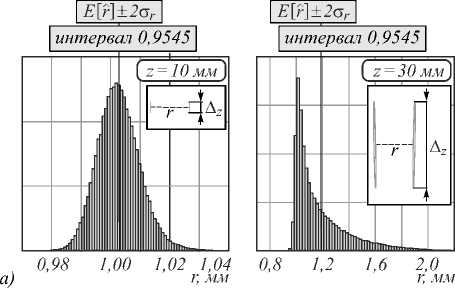
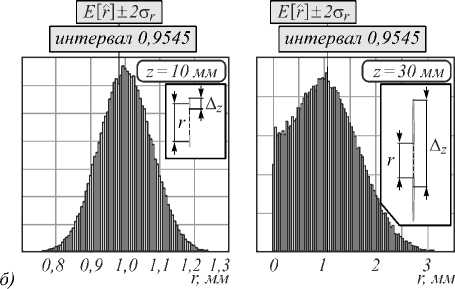
Рис. 9. Гистограмма вычисленных значений длины x-отрезка(а) и z-отрезка (б)

Расчёт доверительного интервала при помощи комбинации метода линеаризации или UT-метода с методом интервальных оценок даёт практически одинаковые результаты.

Это вызвано тем, что ПРВ координат вектора x _w ² - x ¹_w близка к НЗР, и, следовательно, среднее значение и матрица ковариации, вычисленные для него обоими методами, примерно одинаковы. Как и ожидалось, полученные таким образом границы интервала являются более широкими по сравнению с результатами моделирования.

Поскольку погрешность измерения 3D-координат точки обладает значительной анизотропией (погрешность z -координаты на порядок превышает значения для других координат), то погрешность измерения длины отрезка зависит как от ориентации отрезка, так и от его расположения в рабочем объеме. Кроме того, вид ПРВ для r ˆ зависит от соотношения длины отрезка и погрешности измерения 3D-координат его концов, что приводит к различному смещению доверительного интервала для отрезков разной длины, расположенных на одном расстоянии.

Влияние параметров UT-метода. Как показано в работах [25, 26], точность, обеспечиваемая UT-методом, в значительной степени зависит от выбора параметров самого метода. Для рассматриваемой задачи поиск оптимальных значений параметров, описанный в этих работах, неприменим, поскольку требует отдельного и достаточно большого времени на обучение. Тем не менее, необходимо провести анализ влияния параметров UT-метода на результат оценки погрешности. Для этого повторим проведённые ранее расчёты для трассировочной модели при изменении параметра κ от 0 до 8 (рис. 10).

х-отрезок z-отрезок

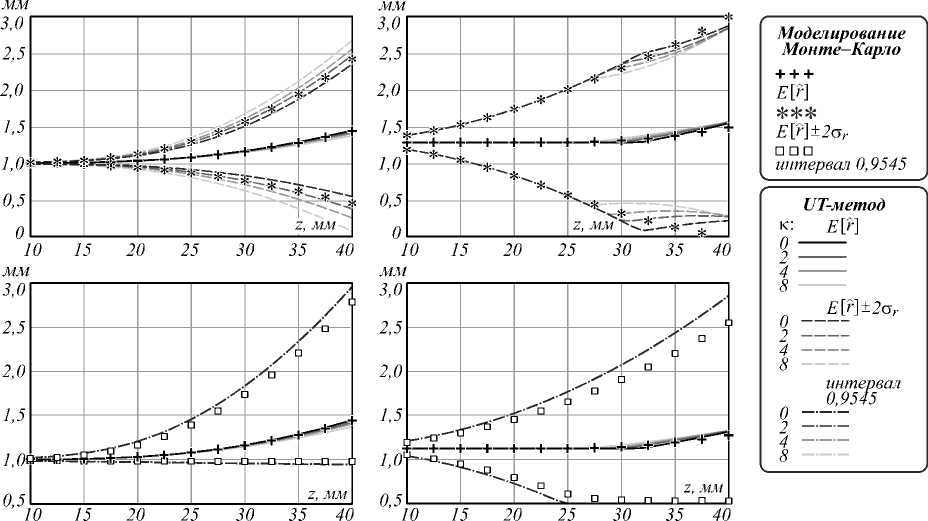
Рис. 10. Оценки погрешности измерения длины отрезка в зависимости от z-координаты при различных параметрах UT-метода

Таким образом, при изменении параметра κ оценки смещения и СКО могут заметно изменяться (до 25% в случае СКО). В то же время для z-отрезка при z менее 25 мм (где ПРВ приблизительно соответствует НЗР) изменение параметра мало влияет на результат. Рассчитанные при помощи комбинации с интерваль- ным анализом границы интервалов практически не изменяются (разница менее 0,2%).

Заключение

Результаты проведенного исследования показывают, что UT-метод является наиболее универсальным методом для оценки погрешности измерений в задачах проектирования стереоскопических систем. Данный метод позволяет работать с алгоритмом вычисления 3D-координат и алгоритмом измерения геометрических параметров как с «черным ящиком» и требует лишь их наличия в реализованном виде. В отличие от метода линеаризации, UT-метод не требует дифференцирования оценочной функции, входящей в алгоритм вычисления 3D-координат. Таким образом, этот метод позволяет сравнивать различные оптические схемы системы регистрации и описывающие их ММФИ, а также различные алгоритмы на этапе проектирования, не внося изменений в сам метод оценки погрешности. UT-метод и метод линеаризации показывают схожие результаты в задаче оценки погрешности измерения 3D-координат точки, в то время как UT-метод позволяет получить более точные результаты при оценке длины отрезка.

Полученные результаты свидетельствуют о том, что среднее значение и матрица ковариации являются достаточным описанием погрешности измерения 3D-координат точки, поскольку полученная ПРВ близка к НЗР. Напротив, для измерений геометрических параметров, таких как длина отрезка, площадь и пр., ПРВ может быть заметно несимметричной. В таком случае целесообразно использовать для описания погрешности измерений среднее значение и доверительный интервал и применять для их оценки предложенную в данной работе комбинацию UT-метода и метода интервальных оценок.

Поскольку погрешность измерения 3D-координат точки обладает значительной анизотропией, то погрешность измерения длины отрезка зависит не только от его расположения в рабочем объеме, но и от его ориентации и длины. Этот результат справедлив и для измерения площадей, а также других геометрических параметров. Это обстоятельство должно быть учтено при проектировании и эксплуатации стереоскопических измерительных систем.

Рассмотренные в работе методы представлены в общем виде и могут быть использованы не только для классических двухкамерных стереоскопических систем, но и для устройств с большим количеством камер, а также для активных триангуляционных систем. Полученные результаты могут быть полезны для проектирования стереоскопических систем, в частности, усовершенствования программного обеспечения.

Работа выполнена за счет гранта Российского научного фонда (проект №17-19-01355). Анализ методов оценки погрешностей путём сравнения с результатами моделирования по методу Монте-Карло для проективной и трассировочной моделей систем регистрации осуществлен при поддержке Российского фонда фундаментальных исследований (проект 17-29-03469).