Оценка погрешности методов Рунге-Кутты в задаче уменьшения кинетического момента микроспутника

ПОСТАНОВКА ЗАДАЧИ

В современной космонавтике при управлении вращательным движением микроспутника наиболее часто используются магнитные системы управления, которые основаны на взаимодействии магнитного поля спутника с геомагнитным полем [1, 2]. Такие системы в основном используются на микроспутниках, поскольку для них характерны небольшими управляющими моментами. Электромагнитные катушки применятся в современных системах управления ориентацией спутников также для уменьшения кинетических моментов двигателей-маховиков [3].

При движении по орбите на спутник оказывают влияние различные возмущающие силовые факторы [4-6]. Кроме того, в процессе отделения от базового космического аппарата микроспутник приобретает остаточные угловые скорости [7], которые требуется минимизировать для обеспечения требуемой его ориентации. Этап управления, при котором происходит минимизация угловых скоростей, называется предварительным успокоением микроспутника. Предварительное успокоение вращательного движения может производится за счет взаимодействия магнитного поля электромагнитов с геомагнитным полем.

Пусть на борту микроспутника находятся три магнитометра, расположенные вдоль главных осей инерции. В качестве управляющих органов используются три электромагнита, расположенных вдоль главных осей инерции микроспутника.

Математическая модель системы управления успокоением микроспутника включает динамические и кинематические уравнения Эйлера. Ди

намические уравнения вращательного движения

спутника имеют вид: ^—

—+(— x K = M— + M ,   (1)

dt                 ^{с p}

——

K = ( K x , K y , K z ) - вектор кинетического момента микроспутника; to = ( to x , to , to _z ) – вектор угловой скорости микроспутника;

где

M = (M ,M ,M ) - вектор управляющего c cx — cycz момента; M = (M , M , M ) - вектор p px , py , pz возмущающих моментов.

Механический управляющий момент, дей

—— ствующий на микроспутник спутник M c , в проекциях на оси X,Y,Z главной связанной системы координат OXYZ имеет вид:

cx

M cy

= L В -LB, y z z y ,

= LB - LB, z x x z,

cz x y y x ,

где L = ( L x , L_y , L_z ) - вектор магнитного момента микроспутника.

Предположим, что закон управления вектором магнитного момента электромагнитных

катушек при предварительном успокоении имеет

вид [8]:

——     ——

^——     ъ- K x B

L =- kc ~^2~

B

Здесь k _c – коэффициент управления, B – модуль вектора магнитной индукции геомагнитного поля.

При определении углов ориентации применялись кинематические уравнения Эйлера, записываемые в следующем виде:

d O / dt = to z cos ф + to y sin ф + to YM sin y - to z_M cos y ;

d y / dt = ( to z sin ф - to y cos ф ) / sin 0 - ^-to хм + ^to M tg O cos y + S) zM ctg O sw;

d ф / dt = to x - d y / dt cos O - to _ZM sin O sin y .

Здесь ω ^~ _xм , ω ^~ _yм , ω ^~ _zм – угловые скорости вращения магнитной системы координат относительно неподвижной геоцентрической системы координат [5].

Численное решение системы из уравнений (1), (4) рассматривается совместно с решением уравнений, характеризующих движение микроспутника по орбите. Решение осуществляется

Конкретный метод определяется числом s и коэффициентами b _i , a_ij и c _i . Эти коэффициенты упорядочивают в таблицу [9], называемую таблицей Бутчера. Таблица Бутчера при использовании формулы Дормана-Принса содержится в [9]. Используя коэффициенты из указанной таблицы, составим формулы для семиэтапного метода Рунге-Кутты:

k = f ( ^х п . У п );

• ^k 2 = f ( x ⁺ 5 h . У п ⁺ 5 ^k 1 h );

3           3      9

• k, = f ( x„ + — h , У„ + h (— k . +— k ₂));

3 n , n 12

^k 4 = f ( x

посредством использования двух явных методов: четырехэтапного и семиэтапного методов Рунге-Кутты. В семиэтапном методе используется формула Дормана-Принса [9]. Четырехэтапный метод является классическим, и в дальнейшем будем использовать сокращенное название РК4.

^k 5 = f ( x ,

^k 6 = f ( ^x „

^k 7 = f ( x „

ЯВНЫЙ ОДНОШАГОВЫЙ СЕМИЭТАПНЫЙ МЕТОД РУНГЕ-КУТТЫ (РК7)

Семейство явных одношаговых методов Рунге-Кутты задается формулами

s

Уп+1 = Уп +Х Ьк, i=1

где h – величина шага интегрирования. Здесь вычисление нового значения проходит в s этапов: k1 = hf (xn , Уп ), k2 = hf(xn + C2h, Уп + a21 ki), ...

^ks = ^{hf (} x n ^{+ C}s h , У п ⁺ a s 1 ^k1 ⁺ a s 2 ^k 2 ⁺ ... ⁺ a s , s - 1 ^ks - 1 ).

+ h, y„ + h( k, -   k, +

• 5 ^{, n} 45¹15²9³

• 8        19372    25360    64448212

+ h, y„ + h(-------k,--k, +--k, -

• 9    ^{, n} 6561 ¹ 2187 ² 6561 ³729 ⁴

9017    355    46732    495103

• + h, y + h(      k, —     k7 +        k-, +     k. —k

• ^{, n} 3168 ¹33 ² 5247 ³176 ⁴ 18656 ⁵

35     500    125

+ h , у + h (----- k . +-- k , +-- k.

^{, n} 384 ¹ 1113 ³192 ⁴

35     500    125

y„,, = y„ + h ( k, + k , + k.

^{п + 1 п} 384 ¹ 1113 ³ 192 ⁴

^^^^.

--k= +

6784 584 6

k +

584 6

РЕЗУЛЬТАТЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ

Четырехэтапный и семиэтапный (5) методы Рунге-Кутты для решения системы дифференциальных уравнений, включающей уравнения (1), (4) реализуются с помощью программы, интерфейс которой показан на рис. 1.

В интерфейсе программы вводятся значения моментов инерции ( I_x , I_y , I_z ) микроспутника, начальные условия ( to x (0), to _y (0), to z (0), 0 (0), y (0), ф (0)) для интегрирования дифференциальных уравнений (1) и (4), шаг ( h ) и конечное время интегрирования ( t _кон ) .

Результаты расчетов с помощью программы имеют табличный вид в файле формата «txt.».

Приведем пример расчета в программе с

Введите значения:

Исходные данные:

Начальные условия:

lz |40

Рис. 1. Интерфейс программы

параметрами по умолчанию, которые показаны на рис. 1, методами РК4 и РК7, но шаг интегрирования зададим равным h = 0,4. Результаты численного интегрирования приведены на рис. 2, 3.

Как следует из рис. 2, 3, результаты расчётов с использование двух методов РК4 и РК7 совпадают, что говорит о малой погрешности численного интегрирования.

Рассмотрим, как зависит погрешность результатов, которые находятся с помощью методов РК4

-----

------ось,?

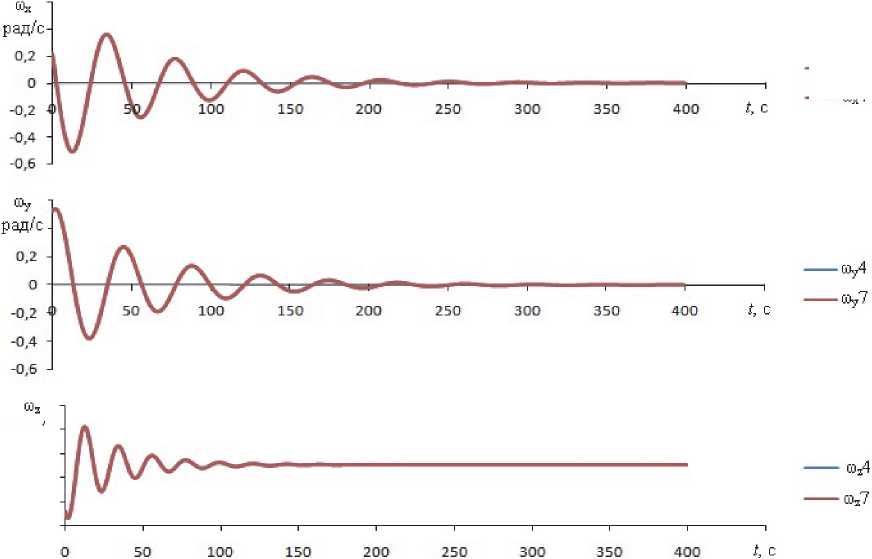
Рис. 2. Графики co x ( t ) , to y ( t ) , to z ( t )

рад/с -

0,41 -

0,405 -

0,4 -

0,395 -

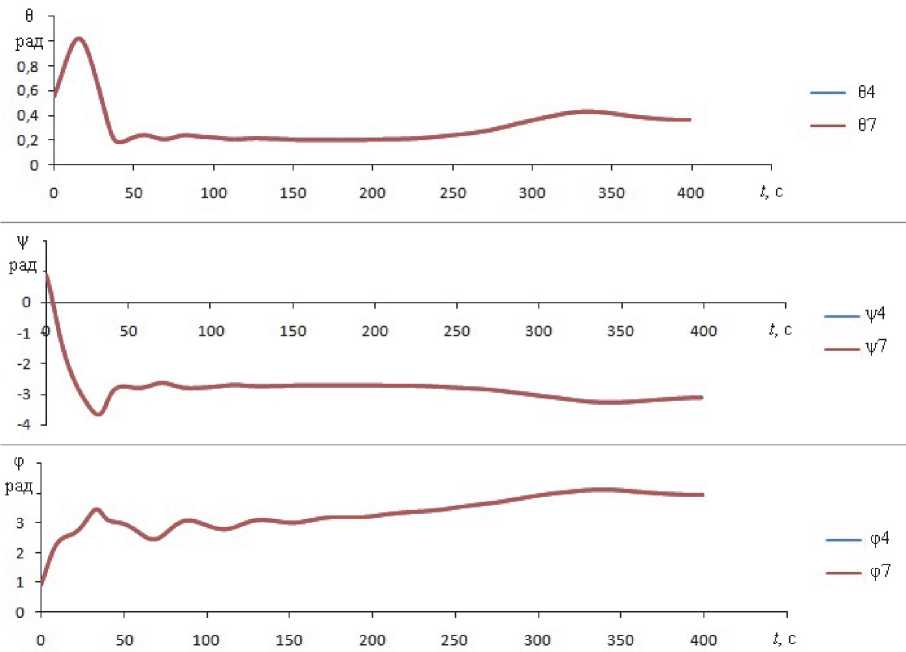
Рис. 3. Графики 0 ( t ) , / ( t ) , ф (t )

Таблица 1. Расчет погрешностей интегрирования при использовании РК4 и РК7

h tкон С V ,% ’^ ' ,% £e,% ev,% £Ф,% 0,01 400 0 0 0 0 0 0 0,05 400 9,35E-06 3,95E-05 1,99E-07 1,71E-05 2,00E-06 2,70E-06 0,1 400 1,92E-03 2,77E-03 2,04E-06 1,55E-05 2,47E-05 1,28E-05 0,2 400 3,08E-03 1,44E-01 3,78E-05 1,54E-03 3,60E-04 4,70E-04 0,3 400 1,53E-02 1,27E-01 1,55E-04 3,46E-03 3,39E-03 3,12E-03 0,4 400 6,92E-01 3,86E-01 4,45E-04 8,27E-03 3,62E-03 9,87E-03 0,5 400 2,90E+00 3,60E-01 9,58E-04 1,61E-02 3,79E-03 1,68E-02 0,6 400 1,65E+01 1,04E+00 1,72E-03 2,39E-02 5,69E-03 2,55E-02 0,7 400 2,08E+01 6,16E+00 2,68E-03 2,95E-02 1,27E-02 3,60E-02 и РК7, от величины шага интегрирования. Для это го составим табл. 1, где εωx,εωy,εωz,εθ,εψ,εϕ – расхождение результатов, поyлучаемых метода-   1.

ми РК4 и РК7 в процентах.

В табл. 1 содержатся величины расхождения 2.

результатов расчетов, определяемых посредством вычисления расхождений угловых скоростей и углов ориентации при использовании четырехэтапного и семиэтапного методов Рунге-Кутты.

Из табл. 1 следует, что чем больше шаг интегрирования, тем больше величина расхождения решений между «РК4» и «РК7». При шаге 0,01 погрешность сводится к величинам порядка 10–9. При шаге большем 0,6 погрешность превышает 5%.

ВЫВОДЫ

Явные одношаговые методы Рунге-Кутты позволяют эффективно решать задачи по моде- 6. лированию процесса успокоения вращательного движения микроспутника. Результаты численного моделирования показывают, что при шаге h < 0,4 интегрирования системы дифференци-  ^7.

альных уравнений расхождение результатов при использовании семиэтапного метода Рунге-Кутты и классического метода РК4 не превышают 8. и 1%. Однако, при моделировании движения микроспутника на значительных интервалах времени следует использовать методы более точные, чем РК4.