Оценка погрешности определения среднеквадратического значения сигнала, обусловленная несоответствием гармонической модели виду реального сигнала

В измерительной технике существует большое число приложений, когда за предельно короткий отрезок времени необходимо идентифицировать сигнал, относящийся к перечню априорно известных моделей. Если, например, гармонический сигнал определенной частоты при изменении фазы или амплитуды выходит за пределы установленного допуска, то принимается решение о наличии короткого замыкания, нарушении работоспособности какой-либо контролируемой цепи, устойчивой недостоверности данных в информационном канале и т.п. При этом, несвоевременное отключение питания, переключение на резервную цепь или измерительный канал часто равнозначно катастрофическому отказу всего объекта в целом [1, 3]. В телекоммуникационных системах одним из актуальных направлений повышения скорости передачи данных рассматривается мгновенное определение параметров манипулированных гармонических сигналов, передаваемых по узкополосному каналу [2].

МЕТОДЫ ОЦЕНКИ ВЛИЯНИЯ СОСТАВЛЯЮЩИХ ПОГРЕШНОСТИ НА ПОГРЕШНОСТЬ РЕЗУЛЬТАТА ИЗМЕРЕНИЯ

Т) и фазу ф, может быть составлена система трех уравнений решение которой позволяет определить искомые параметры сигнала:

А sin (mt, + ф) = x (t,}, < А sin (mt2 + ф) = x (t2);

А sin (mt3 + ф ) = x (t3)

Если отсчеты t ₁ , t ₂ и t ₃ равномерно распределены по периоду Т , то приходим к известному решению, вытекающему из теоремы Котельникова. Однако равномерное распределение отсчетов по периоду предполагает известным значение самого Т , при этом время измерения приблизительно равно периоду.

Значительно сократить время измерения позволяет использование метода измерения интегральных характеристик гармонических сигналов [3], согласно которому мгновенные значения сигнала берутся через одинаковые (в общем случае произвольные) интервалы времени Д t , первое из которых взято в произвольный момент времени:

А sin (mt, + ф ) = x (t,);

< А sin [(mt, + mAt) + ф] = x(t2);

А sin [(mt, + 2mA t) + ф] = x (t 3).

В данном случае время измерения не зависит от периода сигнала, а определяется в основном длительностью интервала времени Д t . В общем случае время измерения меньше периода сигнала.

Выражение для среднеквадратического значения сигнала (СКЗ) гармонического сигнала имеет вид [3]

Х СК 3

х (t i)2 х 2 (12 )-х (13 )х (t, )- х 2 (t, )) 2 2 х (t2 )Vх 2 (t2 )- х (t3 )х (t 1 ) J

, (1)

где x ( t 1) = A sin a 1 ; x ( t 2 ) = A sin ( a 1 + ®A t ) ;

x ( t 2 ) = A sin ( ® 1 + 2® A t ) ; ® 1 - начальная фаза сигнала.

Одной из основных проблем рассматриваемого метода является анализ точности измерения. Если реальный сигнал совпадает с гармонической моделью, то получается методически точный результат. При несоответствии модели виду реального сигнала оценки параметров могут существенно отличаться от оптимальных.

В соответствии с общей методикой метрологического анализа аппроксимационных методов, алгоритмов и средств [4] оценки результирующей погрешности определяются целями измерений и обработки результатов. В общем случае, качество решения аппроксимационной задачи оценивается некоторой результирующей погрешностью, включающей в себя все составляющие, определяющие несоответствие модели и моделируемой зависимости. При случайных сигналах это интегральные, как правило, среднеквадратические оценки. При детерминированных сигналах могут быть получены более жесткие оценки равномерного приближения. Однако для получения таких оценок необходимо знать вид реальной аппроксимируемой зависимости.

Для оценки отклонения модели от реального сигнала можно использовать:

• - наибольшее отклонение значений модели от соответствующих значений сигналов

• 2. С помощью определения погрешности измерения интегральной характеристики как функции, аргументы которой заданы приближенно с погрешностью, соответствующей отклонению модели от реального сигнала.

A x max = sup I x ( t )- xM ( t, « )| = где Yp - расчетное значение интегральной характеристики, определенное для реального сигнала.

Такой метод можно использовать для прогнозирования погрешности и выявления области применяемости метода измерения интегральной характеристики согласно (1) исходя из требований по точности при известных спектрах реальных сигналов.

Погрешность вычисления значения функции, аргументы которой заданы приближенно, может быть оценена с помощью дифференциала этой функции, если .погрешности аргументов достаточно малы и допустима замена приращений функции дифференциалами. Если известны только предельные абсолютные погрешности аргументов, то при вычислении дифференциалов необходимо для всех производных брать их абсолютные значения.

В зависимости от того как производится оценка отклонения модели от реального сигнала, возможны три подхода к определению погрешности.

Считая, что предельные абсолютные погрешности аргументов соответствуют наибольшему отклонению, определяемому согласно (2), то для интегральной характеристики Y = F [ x ( t 1 ), x ( t ₂ ), ... x ( t m ) ] получим

= sup

Ю

Z a k V k ( t )^{- x} M ( t , ^a ) ;

k=0

A Y = ( Y ) x ( t a + ( Y ) x ( t ₂ ) + ... + ( Y ) x ( t m ) A x max . (4)

- среднеквадратическую погрешность

<7 2

b - a

b2

J[x(t)-Xm (t,a)] dt =

a

Если считать, что предельное значение абсолютных погрешностей аргументов определяется через среднеквадратическую погрешность с т в соответствии с (3), то

b - a

b HA               rx 12

J Z ak^k ( t )- xM ( t,a ) dt.

^{A Y} = ^{( Y} ) x ⁽ t 1 ) ^{+ ( Y} ) x ⁽ t 2 ⁾⁺ ... ^{+ ( Y} ) x ⁽ t m ) ^C . (5)

a

k=0

В общем случае для оценки влияния составляющих погрешности, обусловленных несоответствием модели виду сигнала, на погрешность результата измерения той или иной интегральной характеристики сигнала Y = F [ x_M ( t , a ) ] , определяемой в соответствии с (1), можно использовать следующие предлагаемые методы.

1. С помощью расчетного значения интегральной характеристики реального сигнала и определения относительной погрешности

Ax (ti ) = x (ti)-xM (ti, a);

^{A x ( t}m ) = ^{x ( t}m ^{)- X}M ^{( t}m , ^a ) , то

A Y = Ax (t1 )(Y)‘ x (ti ) + Ax (t 2 )(Y)‘ x (12)+ ...Ax (tm Xy )‘ x (tm)

При использовании данного метода относительная погрешность равна

§ =

^Y — ^Yp

Y p

5 = AY

^{. p}

3. Третий метод предусматривает экспериментальное определение погрешности. Для этого производится измерение интегральной характеристики Y = F [ x(t , a ) ] образцовым средством измерения с метрологическими характеристиками, обеспечивающими возможность его использования в условиях реального сигнала, и сравнение с результатом измерения Y прибором, использующим аппроксимационный метод (1).

В общем случае, при наличии в сигнале высших гармоник (помех) мгновенные значения сигнала в моменты времени t ₁ , t ₂ и t ₃ можно представить в следующем виде:

ответствии с (2):

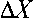
max

= sup

to

2 Ak sin ( krot + ka + vk ) — k=

- A sin (rot+ax )|

Если параметры первой гармоники реального сигнала совпадают с параметрами сигнала, соответствующего гармонической модели, то (10) примет вид

AXmax

to

= sup A ^ h_k sin ( k ro t + k a_i +v _{i k} ) (Ц)

k= 2

x '(ti ) = Ai

sin a + 2 h k sin⁽ kai + V i k ) ; k = 2                     _

Выражение (11) принимает максимальное

to

x'(t2) = A sin(a+roA)+2hsin(ka+vk + kroA) ;(7)

значение

to

A i 2 h k , если k = 2

| sin ( k ro t + k a _i + v _{i k} ) = i ,

k=2

x ( t 3 )= A

tosina + 2Ma) + 2hk sinkai + vik + 2kroAt)k=2

, (8)

где V i k - начальная фаза k -той гармоники относительно первой; h_k - коэффициент k -той гармоники.

ОСОБЕННОСТИ ОПРЕДЕЛЕНИЯ

ПОГРЕШНОСТИ, ОСНОВАННОГО НА ПРИБЛИЖЕННОМ ИЗМЕРЕНИИ ИНТЕГРАЛЬНОЙ ХАРАКТЕРИСТИКИ

т.е. при V _{i k} = у ⁽2 q ^{+ i)+ k} a , где q = 0; 1.

Например, когда в сигнале присутствует первая и третья гармоники, из (9) получим

5 скз

X

=_h3A.

= 3 ■ I i + ctga

^ i + h 2 sin a  2sin roA t

X

ctga sin (ai + 2roAt)    sin (ai + 2roAt)

^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^K  ^^^^^^^^* ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^H

-

sin ro A t

sin a _i sin( a _i + ro A t )

Рассмотрим второй метод оценки, базирующийся на определении погрешности измерения интегральной характеристики как функции, аргументы которой заданы приближенно с погрешностью, соответствующей отклонению модели от реального сигнала.

Допуская, что предельные абсолютные погрешности аргументов соответствуют наибольшему отклонению, определяемому согласно (2), то в соответствии с (4) для СКЗ сигнала имеем

sin( a + ro A t )

+

^{A X} скз =

⁽ XСКЗ ) ^{x (} t i ) ^{+ (} XСКЗ ) ^{x (} t 2 ) ⁺

^{+ A (} X СКЗ ) ^{x (} t 3 )

max .

Относительная погрешность д_СКЗ равна

5  =___ max

°СКЗ   у хСКЗр L

( ^ХСКЗ ) ^{x (} t i ) ⁺ ( ^ХСКЗ ) ^x t 2 ) ⁺

^{+ ( Х}СКЗ ) ^x t 3 )

Определим предельное значение Д Х _max в со-

ctg a sin a

2 cos a cosai sin(ai + roAt) ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^k ^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^k ^^^^^^^k ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^k sin roAt sin(ai + roAt) sin2 roAt

2 sin a _i sin ro A t

cos a _i          i

^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^  ^^^^^^^»  ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^k sin roAt sin(ai + roAt)

+

r .(12)

Eсли считать, что предельные абсолютные погрешности аргументов соответствуют отклонению модели от реального сигнала, определяемому через среднеквадратическую погрешность в соответствии с (3), то согласно (5)

^{A X}СКЗ = ^{( Х}СКЗ ) ^{x (} t i ) ^{+ ( Х}СКЗ ) ^{x (} t 2 ) ^{+ ( Х}СКЗ ) ^{x (} t 3 ) °".

Определим значение среднеквадратической погрешности согласно (3)

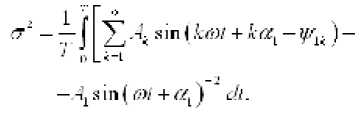
Если параметры первой гармоники реального сигнала совпадают с параметрами сигнала, соответствующего гармонической модели, то в силу ортогональности тригонометрических функций (13) примет вид

5 скз

h3

V1 + h32

'( ХСКЗ ) x (ti) +

+ ( ХСКЗ ) x (t2) + ( ХСКЗ ) x (t3)

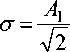
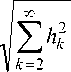
т.е. (14) соответствует среднеквадратическому значению высших гармоник Х_Г .

Относительная погрешность д_СКЗ равна

5 скз

Х Г

Y

СКЗ

( Хскз ) x (ti) + ( Хскз ) x (t2) ++ ( ХСКЗ ) x(t3)    kC ( ХСКЗ ) x(ti) +

V

+ ( ХСКЗ ) x (t2) + ( ХСКЗ ) x (t3)  ,

где k_C - коэффициент несинусоидальности.

Для рассматриваемого случая, когда в сигнале присутствует первая и третья гармоники, из (15) получим

Анализ показывает, что при наличии в сигнале первой и третьей гармоник погрешность д_СКЗ , определенная согласно (16), в 2 раз меньше аналогичной погрешности, вычисленной в соответствии с выражением (12).