Оценка погрешности реализации метода измерения параметров, основанного на формировании и сравнении ортогональных составляющих напряжения

В настоящее время имеются два основных направления развития методов и систем измерения параметров периодических сигналов.

Первое направление связано с попытками увеличения точности определения отдельных параметров периодических сигналов за счет обработки результатов измерений. В них отсутствует системный подход к определению всего комплекса параметров. При этом вопросы сокращения времени измерения не рассматриваются [1 - 3].

Второе направление используется для измерения параметров периодических сигналов, форма которых близка к гармонической модели [4]. Методы основаны на предположении о соответствии входных сигналов гармоническим моделям, что значительно упрощает алгоритм определения параметров и значительно сокращает время измерения. Методы и, реализующие их системы, используют определение параметров сигналов по отдельным мгновенным значениям напряжения и тока, которые не связаны с длительностью периода входного сигнала. Для оценки полученных результатов производится анализ погрешности, обусловленной отклонением реальных сигналов от гармонической модели [5].

Для дальнейшего сокращения времени измерения используют разделение мгновенных значений сигналов в пространстве за счет формирования дополнительных напряжений и токов, которые смещены по фазе относительно входных. При этом определение параметров производят по мгновенным значениям как входных, так и дополнительных сигналов [6].

Упрощение алгоритма определения параметров, а также сокращение аппаратурных затрат обеспечивает реализация методов, в которых в качестве дополнительных используют ортогональные составляющие сигналов [7].

В статье рассматривается новый метод определения параметров и, реализующая его информационно-измерительная система (ИИС), которые основаны на формировании и сравнении ортогональных составляющих напряжения [8].

МЕТОД ИЗМЕРЕНИЯ ПАРАМЕТРОВ НА ОСНОВЕ ФОРМИРОВАНИЯ И СРАВНЕНИЯ

ОРТОГОНАЛЬНЫХ СОСТАВЛЯЮЩИХ НАПРЯЖЕНИЙ

Согласно предлагаемому автором методу производится формирование дополнительного напряжения, сдвинутого относительно входного на 90°. В произвольный момент времени измеряют мгновенные значения входного и дополнительного напряжений и тока, а в момент равенства ортогональных составляющих напряжения измеряют мгновенные значения входного напряжения и тока. Искомые параметры определяют по измеренным мгновенным значениям.

Метод можно пояснить с помощью следующих временных диаграмм (рис. 1).

При гармонических входных напряжении и токе u1 (t ) = Um sin to t; i (t) = Im sin (to t + ф), дополнительное напряжение примет вид u2 (t) = Um cos юt, где Um , Im – амплитудные значения входного напряжения и тока; ф - угол сдвига фаз между входными напряжением и током; го - угловая частота.

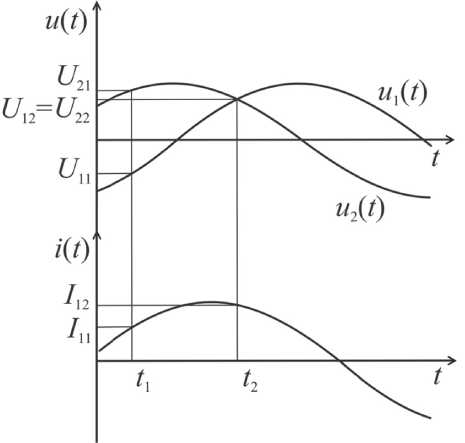
Рис. 1. Временные диаграммы, поясняющие метод

I . п

¹ 12 = I m Sin l Ф + -

После преобразований можно найти выражения для определения основных параметров гармонических сигналов:

• -    среднеквадратические значения (СКЗ) напряжения и тока

^U СКЗ = | ^U 12 | ^{;                (1)}

¹ СКЗ =

^{( 1} 11| ^U 12,    ¹ 12 U 21 ^{)+( 1} 12 U 11    ¹ 11 \^U 12, ^)] 2

|U 11    U 21|

; (2)

• -    активная (АМ) и реактивная (РМ) мощности

р _ |^U 12 |^{( 1} 11 \^U 12 | ^{- 1} 12 ^U 21 )

P =       U 11 - U 21       ;       ⁽³⁾

Q = ^U 121^{( 1} 12 U 11 - 1 11 ^U 12 1)         ₍₄₎

и 11 - U ₂₁

В произвольный момент времени (момент времени 1 1 на рис. 1) сигналы будут равны:

U 11 = U m sin a ; U 21 = U m cos a i ;

1 11 = I m ^Si n ( ^a i +ф ) , где a 1 - начальная фаза входного сигнала напряжения в момент времени 1 1 .

В момент времени, когда ортогональные составляющие напряжения будут равны (момент времени 1 2 на рис. 1), мгновенные значения напряжения и тока примут вид:

U 12 = U_m sin a 2 ; U 22 = U_m cos a 2 ;

112 = Im sin(a2 +Ф) , где a2 - фаза входного напряжения в момент времени t2.

Учитывая, что равенство ортогональных со- ставляющих напряжения U12 и U22 наступит при

П

угле a ₂ =   + п 1 (где l = 0,1 ), мгновенные значе-

4 _U ния сигналов примут следующий вид: U = — m 12       2

;

Схема ИИС, которая может быть использована для реализации метода, приведена на рис. 2.

В состав устройства входят: первичные преоб -разователи напряжения ППН и тока ППТ, аналогоцифровые преобразователи АЦП1 - АЦП3, фазосдвигающий блок ФСБ, компаратор КОМП, контроллер КНТ, шины управления ШУ и данных ШД.

АНАЛИЗ ПОГРЕШНОСТИ РЕАЛИЗАЦИИ

МЕТОДА ИЗМЕРЕНИЯ ПАРАМЕТРОВ

ГАРМОНИЧЕСКИХ СИГНАЛОВ

Одним из недостатков ИИС, которая реализует данный метод, является погрешность по напряжению (погрешность по модулю) фазо-сдвигающих блоков. Данный вид погрешности заключается в том, что ампитуда входного напряжения может отличаться от амплитудного значения напряжения на выходе ФСБ.

Если амплитудные значения напряжений на входе и выходе фазосдвигающего блока будут отличаться на величину A U m , то мгно-

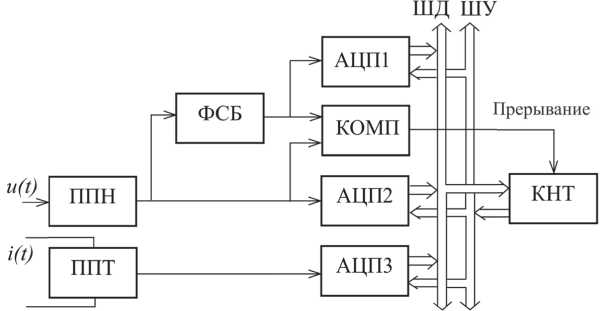
Рис. 2. Схема ИИС, реализующей метод

венные значения дополнительного напряжения примут вид: U ‘ 1 = ( U . + A U m ) cos a ₁ и и 22 = U . + А U . ) cos a ₂ . Поскольку мгновенное значение U 2 1 используется для определения информативных параметров, а U 2₂ участвует в сравнении ортогональных составляющих напряжения, то неизбежно возникает погрешность.

При анализе влияния данной погрешности на результирующую погрешность определения параметров может быть успешно использована известная методика оценки погрешности результата измерения интегральной характеристики как функции, аргументы которой заданы приближенно с погрешностью, соответствующей отклонению модели от реального сигнала, рассмотренной в [9].

Если считать, что мгновенные значения входных сигналов напряжения и тока измерены без погрешности, то можно определить предельные значение абсолютных погрешностей измерения

СКЗ тока, АМ и РМ:

г	д 1 СКЗ		01 СКЗ	^
V	d U 22		a u 2,	/

А U ;

^{A I}СКЗ =

А Р = V	d p	+	д p '	A U ; /	(6)
	а и 22		д U 2^
г A Q = \	' а Q	+	д Q	A U . )	(7)
	д и : 2		а и 21

Из выражений (5) – (7) и (2) – (4) можно найти относительные погрешности (ОТП) измерения СКЗ сигналов и приведенные погрешности (ПРП) определения АМ и РМ:

51СКЗ = hm I1 - C0S V(Sin Ф + C0SФ) +

+ T2|sin ( a ₁ + ф )( cos ф- sin ф ) ] /^1п a ₁ - cos a ₁ ;(8)

Y p = h.[ sin ф| + |sin (ai +Ф)+

• + cos ф ( sin ф - cos ф )|] /|sin a ₁ - cos a ₁ ; (9)

Y Q = h . [ sin ф| + V2|sin ф ( sin a ₁ - cos a ₁ ) -

• - sin ( a ₁ +ф )| ] /|sin a ₁ - cos a ₁ ,    (10)

  ГДе h . =

  
  

  A U . U m

  
  

Из анализа выражений (8) – (10) следует, что ОТП определения СКЗ тока и ПРП измерения АМ и РМ зависят от гармонического состава сигналов, угла сдвига фаз между входным напряжением и током ф и момента начала измерения, характеризуемого начальной фазой a ₁ .

Графики зависимости ОТП измерения СКЗ тока и ПРП определения АМ и РМ приведены на рис. 3 – 5.

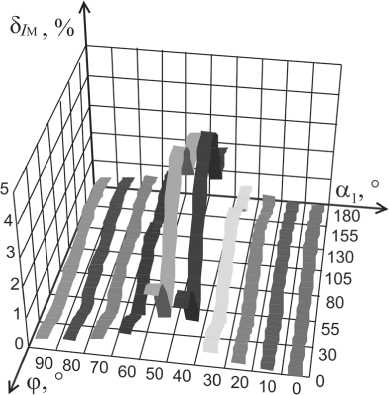
Рис. 3. Графики зависимости 5_ш от ф и a ₁

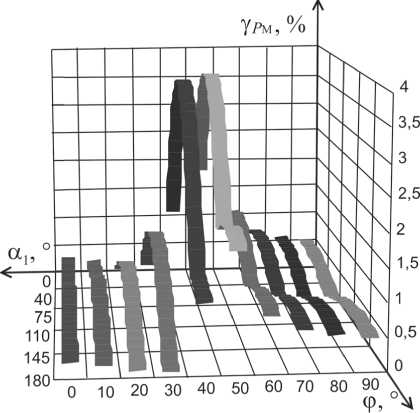
Рис. 4. Графики зависимости Y P _М от ф и a ₁ л

Y0M) %

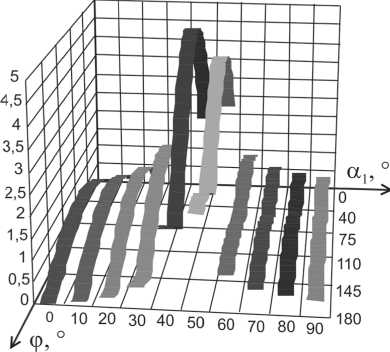
Рис. 5. Графики зависимости y q _м от ф и a ₁

Анализ показывает, что при a ₁ = 45 ° знаменатели выражений (8) – (10) обращаются в ноль. Этим объясняется резкое увеличение погрешностей в окрестностях 45º (начальные фазы, равные 40º и 50º на рис. 2 - 4).

Другим видом погрешности, которая может возникать при реализации методов, использующих ортогональные составляющие сигналов, является частотная погрешность фазосдвигающего блока, которая может привести к тому, что при изменении частоты входного сигнала угол сдвига фазы ФСБ будет отличаться от 90º.

Если при анализе влияния частотной погрешности фазосдвигающих блоков на погрешность

j          Г др

Y P _р — <  sin ( а 1 + ф1 cos ^

. др

- sin

Г др)   . Г др)

cos ф- + sin ф-

Г 2 J Г 2 J

Г др)!

х cos l а. +--I> ) 1     2 J

др cos

-

х

. др - sin —

/

результата измерения параметров считать, что углы сдвига фазы ФСБ1 и ФСБ2 отклоняются от

/ [ sin а 1 - cos ( a 1 + др ) ] - cos ф ;

90° на одинаковый угол А р , то дополнительное напряжение примет следующий вид:

и 2 ( t ) — U m sin l ^ю t + ^П + др! — U m cos ( ro t + Др ) ;

Y q р ^— ] ^Sin lФ

др )    Г    др

--I+ cos l ф--

2 J   Г  2

sin а ₁ -

-

Мгновенное значение дополнительного напряжения в момент времени 1 1 будет равно:

U 2 1 = U m cos ( a 1 + Д₽ ) .

В момент времени t ₂ мгновенные значения сигналов примут вид:

и 1 2 — u m sin ^а 2 ; и 2 2 — u m cos ( a 2 + др ) ;

1 12 ^— I m s ^{in ( a} 2 +Ф ) .

sin ( a 1 + ф )

. др

- sin —

др cos

/ [ sin а ₁

. др

- sin — 2

др cos

-

- cos ( a 1 +др ) ] - sin ф . (14)

Равенство U12 и U22 происходит при угле к     др а, — —+ nl--. Если l=0,то мгновенные значе-24        2

Из (11) следует, что погрешность измерения СКЗ напряжения зависит только от А р . При А р =0,1° значение погрешности равно 5 U _р =-0,17%.

На рис. 6 - 8 приведены графики зависимости погрешностей определения СКЗ тока, АМ и РМ от угла сдвига фаз ф и начальной фазы входного напряжения а 1 при А р =0,1° в соответствии с (12) - (14).

ния сигналов будут соответствовать следующим

выражениям:

( п др)

^U 12 ^{— U} m sin - ^- — I S

I п др , )

1 12 ^— I m sin l ~ ^- — ⁺ Ф I .

Используя мгновенные значения сигналов, можно найти погрешности определения параметров:

5 — cos — - sin ^- 1 ;    (11)

^{и р}        2        2

⁵ 1 в ^—

[ • / , / др . др)

< sinla, +ф) cos--sin— I l V 1    \     2        2 J

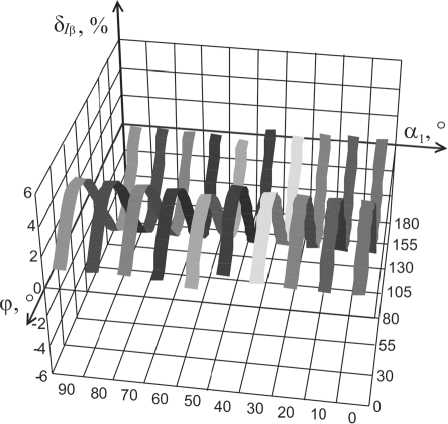
Рис. 6. Графики зависимости 5 I р от ф и а 1

Г др). . Г др) cos l ф-- I + sin l ф-

V 2 J Г 2 J

х

Г др) х cos l а. +

I ¹     2 J

-

др . др

< cos--sin —

2       2

х

х sin ( a 1 +ф ) -

• Г др). Г др)

sin l ф--I+ cos l ф-

Г 2 J Г 2 J

х

х sin а 1 } ²)² / [ V2|sin а 1 - cos ( a 1 + др ) ] - 1 ; (12)

Анализ выражений (12) - (14) и рис. 6 - 8 показывает существенную зависимость погрешностей измерения параметров не только от угловой погрешности, характеризуемой А р , но и от угла сдвига фаз между напряжением и током ф .

При этом ПРП определения АМ в значительной степени зависит еще и от начальной фазы входного напряжения а 1 , то есть от момента начала измерения.

Относительная погрешность измерения СКЗ тока существенно меньше зависит от а 1 , а на

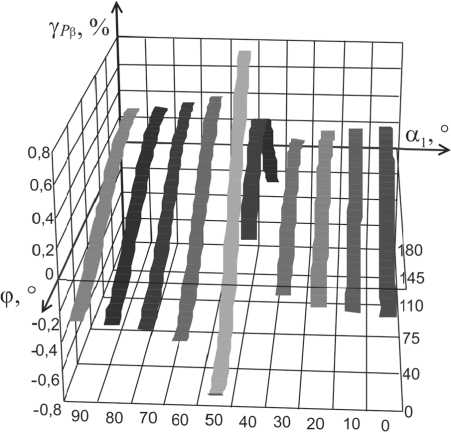
Рис. 7. Графики зависимости γ _{P β} от φ и α ₁

frequency estimation methods for power system signals under nonsinusoidal conditions // IEEE Transactions. Power Delivery. 2005. V. 20, No. 1. P. 366–374.

• 3.    Petrovic P.B., Stevanovic M.P. A new method of determining the amplitude and phase of an alternating signal // Measurement Techniques. 2010. V. 53, No. 8. P. 903-910.

• 4.    Мелентьев В.С., Батищев В.И. Аппроксимационные методы и системы измерения и контроля параметров периодических сигналов. М.: ФИЗМАТЛИТ, 2011. 240 с.

• 5.    Melent’ev V.S., Ivanov Yu.M. Study of the method of measurement of parameters of periodic signals by their instantaneous values using feature points / Science and Education: Materials of the XI International research and practice cjnferenct. Munich, Germany, 2016. Vol. 1. P. 99 – 106.

  
  
  

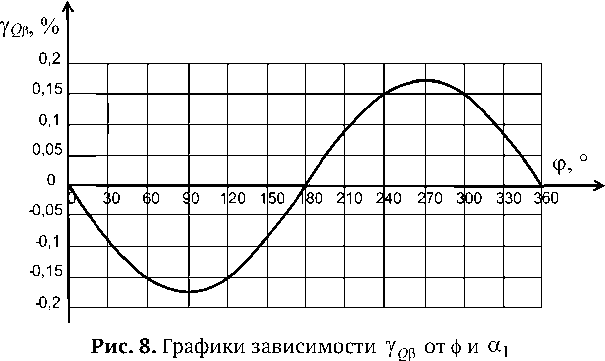
приведенную погрешность определения РМ этот параметр вообще не оказывает влияния.

ЗАКЛЮЧЕНИЕ

Разработанный метод измерения параметров гармонических сигналов позволяет начинать процесс измерения в произвольный момент времени, что сокращает, в общем случае, время измерения. Кроме того, метод прост в реализации и требует незначительных аппаратурных затрат.

Полученные в работе результаты позволяют оценить предельные значения погрешностей определения параметров гармонических сигналов и, следовательно, выбрать области возможного использования метода.