Оценка погрешности синхронизации разнесенных наземных пунктов спутниковой связи

Возможность выполнять высокоточные измерения координат объектов и осуществлять синхронизацию шкал времени с помощью ГЛОНАСС в любой точке земного шара не исключает возможности использования в наземных пунктах спутниковой связи автономных навигационных средств и средств синхронизации. Необходимость этого обусловлена тем, что в тех или иных районах земной поверхности точностные характеристики ГЛОНАСС в значительной степени ослабевают и снижаются до минимального уровня [1-6]. Причинами этого может быть неблагоприятный геометрический фактор, ограничения радиови- димости космических аппаратов, неполнота сети и масса других обстоятельств. Особенно это касается северных и арктических территорий Российской Федерации. Однако потребители навигационного сигнала, в том числе и наземные пункты спутниковых систем связи, предъявляют все более высокие требования к доступности и надежности данных о местоположении и системной шкале времени. На сегодняшний день глубина проработки вопросов теории и возможных направлений решений задач синхронизации наземных пунктов систем спутниковой связи не соответствует запросам практики. Указанные задачи являются актуальными и полностью согласуются с принятой в России концепцией Единой системы координатно-временного и навигационного обеспечения. Вопросам синхронизаций радиотехнических систем посвящены исследования и работы таких авторов как А. Д. Аргунова, С. Н. Малюкова, В. Г. Боровицкого и др. [7].

1. Оценка погрешности синхронизации приемной аппаратуры наземных пунктов спутниковой связи

Система временной синхронизации является важной частью мультипозиционных активных или пассивных наземных радиотехнических систем. Погрешность временной синхронизации наземных объектов должна быть меньше, чем σ _i / c , где σ _i – ошибка измерения координат, c – скорость света. Например, ошибка синхронизации в масштабе времени должна быть меньше 10 нс для достижения ошибки измерения координат менее чем 10 метров. Такая высокая точность может быть обеспечена двухсторонней передачей сигналов синхронизации в диапазоне ультравысоких частот между разнесенными пунктами сети наземных станций спутниковой связи [8].

Шкала времени представляет собой двоичную последовательность, синхронизированную с опорным сигналом и формируемую на ведущем пункте. Опорный сигнал синхронизирует псевдослучайную m -последовательность с периодом 1023

ющая включает в себя аппаратную компоненту, и вторая связана с условиями распространения синхронизирующего сигнала.

Главные факторы сбоя счета времени распространения радиоволны для радиоканала, находящегося около поверхности Земли, - это непостоянность скорости радиоволн и рассеяние радиоволн, вызванное разнородностью рельефа. Уравнение для вычисления скорости радиоволны в пространстве с коэффициентом преломления n имеет вид: c = c ₀/ n , где c ₀ – скорость радиоволны для области свободного распространения.

Коэффициент преломления зависит от ат- 103 мосферного давления, температуры и влажности воздуха. Уравнение для коэффициента преломления имеет вид:

n = 1 + N-10-6, где N = 200...400 для зон вблизи поверхности Земли.

Уравнение для временной задержки распространения радиоволны имеет вид [9]:

^т d = — J ^{n (} ^ ) ^dS ,             (1)

c 0 L где интегрирование выполнено для радиокана-

знака и длительностью составляющего символа в 100 нс. Ультравысокочастотный (УВЧ) сигнал синхронизации представляет собой сдвинутый по фазе несущий УВЧ сигнал с частотой 1065 MГц, промодулированный с помощью псевдослучайного сигнала. Основная доля диапазона частот УВЧ сигнала составляет 20 МГц. Передатчик ведущего пункта излучает синхроимпульсы турникетной антенной, имеющей всенаправленную диаграмму направленности в горизонтальной плоскости. В периферийном (ведомом) пункте m -последовательность синхронизируется с помощью сигнала, полученного от ведущего пункта и модулирует УВЧ несущий сигнал с частотой 625 МГц. Несущий сигнал с фазовым сдвигом излучается также изотропной антенной. Принятый сигнал синхронизирует m -последовательность приемника ведущего пункта. Синхроимпульсы переданных и полученных последовательностей формируют входные сигналы для измерителя временных интервалов.

В ходе проведения натурных испытаний аппаратуры взаимной синхронизации определялась потенциальная точность синхронизации оборудования на наземных объектах с заранее неизвестными координатами, при этом аппаратура синхронизации обеспечивала измерение времени распространения сигнала с одного наземного объекта к другому и формировала универсальные шкалы времени на пунктах. Измеренная временная задержка состоит из двух частей. Первая составля- ла, соответствующего минимальному времени распространения. Необходимо детально знать n как функцию координат для вычисления выражения (1). В большинстве случаев это является проблемой, потому что коэффициент преломления зависит от погодных условий и рельефа подстилающей поверхности. Если среднее значение N оценивается по погодным условиям для некоторой пространственной точки и среднее значение отклонений меньше, чем ΔN, тогда используется выражение (1) для определения флуктуации времени распространения для радиоканала длиной L:

∆ N ⋅ L

∆τ _d

c ₀

Δτ

Следовательно, d = Δ N , где τd – время τd для области свободного распространения.

Экспериментальная оценка разницы отклонений коэффициента преломления для приповерхностных радиоканалов в разных пространственных точках представлена в [9]. Измеряя температуру, атмосферное давление и влажность воздуха в одно время, средняя квадратичная разница ко эффициентов преломления σ = Δ N для пространственных точек протяженностью 103 км будет равна от 2 до 8,5. Экспериментальные измерения были сделаны для городов Кемерово и Томск. Для случая, когда AoN = 10, L = 40 км, по-

(оСМИЧЕскиЕ

АППАРАТЫ И

Том 5

грешность флуктуации времени распространения составит о_т = 1,5 нс. Таким образом, используя среднее знач ^d ение можно определить зависимость времени распространения сигнала от отклонения скорости радиоволны.

и амплитудным детектором. Выражение для расчета величины напряжения выходного сигнала на выходе схемы вычитания имеет следующий вид:

2. Расчет погрешности синхронизации приемной аппаратуры наземных пунктов и эксперементальные результаты погрешности синхронизации разнесенных пунктов

T udiscr (т) = J x (t — т) • U0( t — у)dt — т 0                                     (4)

-j x ( t + T -т ) • U _o ( t + T + T ¹ ) dt .

о                                           ₂'

Корреляционный приемник имеет

Так как m -последовательность периодическая, можно выполнить преобразование (4):

m -последовательность такую же, как и передатчик. Для формирования сигнала временной ошибки между входным и опорным сигналами опорная m -последовательность имеет сдвиг во времени T 1 /2 или минус T ₁/2 для каждого периода последовательности, где T 1 - длительность символа, составляющего последовательность;

T udiscr (t) = J x(t — T) • U0(t + y)dt — 0                  2

T

-[ x ( t + T — t ) • U _o ( t + T -) dt .

о                                     ₂'

т - дискрета временного сдвига, управляющая электронным коммутатором. Блок-схема корреляционного приемника в упрощенном виде изображена на рис. 1.

Пусть

При условии отсутствия рассеяния сигнала синхронизации подстилающей поверхностью и пренебрежительно малого уровня собственных шумов приемной аппаратуры:

x ( t ) = a ■ u₀ ( t) + u_s ( t ) + n ( t ) = Re x ( t ) • e^{j m} ° t , где a • u ₀( t ) - полезный сигнал; u s ( t ) - сигнал, рассеянный рельефом; n ( t ) - собственный шум приемника.

Комплексный вид полезного сигнала:

TT udscr (т) = a0 • U0(t — т) • U0(t — V)dt — О                    2

T

— а ₀ • J U _o ( t — т ) • U _o ( t +—1 ) dt + 0 ²

a • u₀ ( t ) = a • Re A ( t ) • e j * t ) • Jt = = a • Re U ( t ) • Jt ,

T

+ a ₁ • f U _o ( t -т — т ) • U _o ( t —1) dt —

^{1       0        1            0}        2

где уравнение для полезной интегральной амплитуды сигнала:

N

и ( t ) = L U «= ( t - ( i - 1 ) ' Z 1 ) , i =

U 0i = ±1.

Суммарная корреляция входного сигнала и опорной m -последовательности выполняется множителем функции, узкополосным фильтром

T

^— a l • J ^U 0 ⁽ t - ^T 1

T

— т ) • U _o ( t + -^-) dt =

= a 0 •

+ a^ •

K ( т — T^) — K ( т + T ¹ )

+

TT

K ^{( т + т} 1 ^— у)^— K ^{( т + т} 1 ⁺ у)

где   K (τ)  – автокорреляционная функция

m -последовательности.

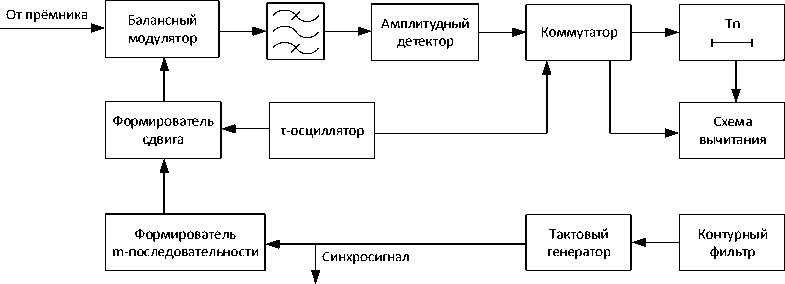
Рис. 1. Блок-схема корреляционного приемника

натора. Характеристика линейная если | т |

На рис. 2 представлена корреляционная функция и характеристика временного дискрими- T

< — , тог- 2

да:

u_dis Дт) = 2 a ¹ .               (7)

discr

T 1

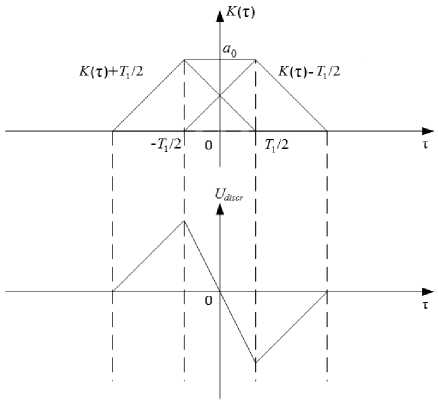
Рис. 2. Характеристика временного дискриминатора

Максимальное значение напряжения на выходе временного дискриминатора соответствует корреляции во времени входа и опорной m -последовательности в условиях без помех. Если отсутствуют собственные шумы приемника, но присутствует рассеяние сигнала из-за рельефа, тогда используется уравнение (5):

T

U dscr ( т ) = a 0 ■ [ и о ( t -т ) • U о ( t - T ") dt о                    ²

-

T

• - a₀ • J U _o ( t + T - т ) ■ U _o ( t + — ) dt + о ²

T

+j Uо(t- т) •Uо(t - "y) dt -о2

T

• -f U _o ( t + T - т ) • U _o ( t + ^T -) dt . о ²

  
  

Сбой счета времени зависит от статистических данных рассеянного сигнала и динамических характеристик следящей системы.

В общем виде, рассеянный сигнал представляет собой сумму отраженных лучей [3; 4; 11]:

N us (t) = Е aiu0(t -тi)’            (9)

i = 1

где a_i – коэффициент амплитуды, τ _i – разница во времени распространения полезного и отраженного сигналов.

Форма сигнала u s ( t ) зависит от пути распространения сигнала, высоты антенн, диаграммы направленности антенн ведущего и периферийных (ведомых) пунктов. Согласно условиям сумма отраженных сигналов (9) может варьироваться от нуля до значения верхней границы. Как правило, сигнал u_s ( t ) является стационарным случайным процессом.

Для операционного анализа следящей системы наиболее интересными являются отраженные сигналы с задержками относительно прямого меньшими, чем ширина дискриминационной характеристики схемы слежения за задержкой. Допустим только отраженный сигнал с коэффициентом амплитуды а 1 , временем задержки т 1 < T 1 и фазовым сдвигом несущей частоты φ₁=0.

Следовательно, принимая во внимание выражение (7):

• ^{2 а}^     ² a-

• udis^er (Т) = — Т + — (Т+Т1), T1         T1

I т< £.

T

I ^т-т 1 <  у.

a

Пусть —- = K j , тогда, исходя из выраже- a ₀

ния (10), ошибка схемы слежения в установившемся режиме, вызванная отраженным сигналом, описывается следующим выражением:

_т = ^Т ' ^K 1

1 + к ’

I Т<-•

Знак «–» в правой части уравнения означает задержку опорной последовательности относительно входного полезного сигнала.

Если количество отраженных сигналов N , тогда выражение (11) преобразуется:

N

Ё т- K ii

• т = - i=1- N----, при | т|<   .

1+Z к

= -

Таким образом, точность синхронизации зависит от разности фаз прямого и отраженного сигналов. Каждый входной сигнал формирует гармонические колебания на входе детектора, амплитуды гармонических колебаний пропорциональны функции взаимной корреляции комплексной огибающей входного сигнала и опорной m -последовательности (рис. 1). Пусть на входе приемника будет три сигнала: прямой сигнал и два отраженных сигнала. Функция взаимной корреляции общего входного сигнала и основной последовательности вычисляется как:

(оСМИЧЕскиЕ АППАРАТЫ И

Том 5

К^ (t) = V( Ko (т) + K (t)cos Ф1 + K2 (T)cos ф2)2 +(K (T)sin ф[ + K (T)sin Ф2 )2, где K 1 (т) - функция взаимной корреляции опорного и прямого сигналов; K2(τ) – функция взаимной корреляции опорного сигнала и второго отражения сигнала; т1 - разница распространения радиоволны первого отражения сигнала и прямого сигнала; τ2 – разница распространения радиоволны второго отражения сигнала и прямого сигнала; φ1 - фаза первого отражения сигнала; ф2 - фаза второго отражения сигнала.

Для формирования m -последовательности ¹⁰⁶ длиной в 1023 знака необходимо смоделировать 10-битный регистр сдвига с обратными связями. Каждый знак m -последовательности состоит из 20 дискретных значений. Число дискретных значений определяет точность моделирования 100/20 = 5 нс. Входной сигнал состоит из прямого сигнала и только первого отражения. В режиме поиска следящей системы синхронизации определяется максимум корреляционной функции и фиксируется время максимума корреляционной функции. В режиме автосопровождения сравниваются

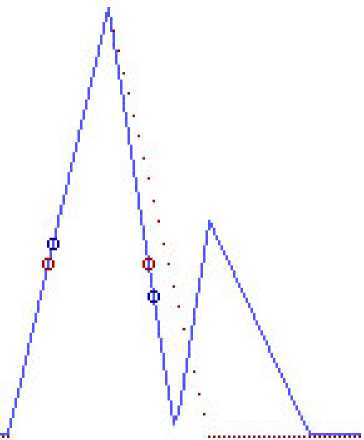
Рис. 3. Функция взаимной корреляции входного и опорного сигналов k1 = a1/a0, a2 = 0, τ2 = 100 нс, φ1 = π, Δt = 10 нс значения К^ (т — 50) и К^ (т + 50). В зависимости от результата сравнения выполняется увеличение на 1 или уменьшение на 1 значения τ до тех пор, пока К2 (т — 50) не станет равно К^ (т). Результаты моделирования для отраженных сигналов с различными параметрами показаны на рис. 3 и 4.

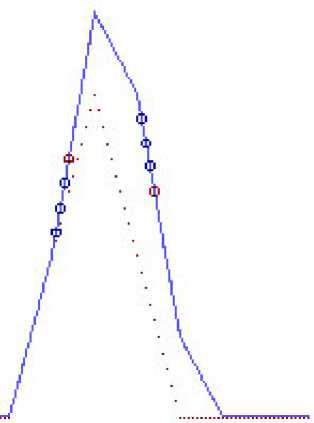
Рис. 4. Функция взаимной корреляции входного и опорного сигналов k ₁ = a ₁/ a ₀, a ₂ = 0, τ₂ = 50 нс, φ₁ = 0, Δ t = 17 нс

Пунктирной линией отображена функция взаимной корреляции опорного сигнала и входного сигнала в условиях отсутствия рассеяния синхронизирующего сигнала. Точки на графике обозначают работу следящей системы в режиме автосопровождения. Погрешность синхронизации приемной аппаратуры наземных пунктов спутниковой связи по результатам моделирования составила менее 5 нс. По результатам экспериментальных испытаний двух наземных пунктов максимальная погрешность синхронизации составила до 60 нс. Результаты измеренных значений задержки синхронизирующего сигнала и погрешность системы синхронизации представлены в табл. 1.

Таблица 1

Результаты экспериментальных испытаний

Номер радиоканала	Измеренная задержка, нс	Среднеквадратичное значение, нс	Реальная задержка, нс	Данные системы синхронизации, м	GPS данные, м	Измеренная ошибка, м
1	54710,02	0,80	54411,48	8167,13	8154,38	4,14
2	72649,50	2,85	72330,76	10853,96	10839,55	5,81
3	55128,19	1,53	54662,89	8204,82	8191,09	5,13
4	55217,42	1,68	54752,12	8218,20	8187,03	11,57
5	55222,40	0,49	54724,04	8213,99	8187,03	18,36

Окончание таблицы 1

6	55222,10	0,54	54723,67	8213,94	8187,03	18,30
7	55226,30	2,03	54727,9	8214,58	8187,03	18,94
8	55232,09	3,70	54733,69	8215,44	8187,03	19,81
9	55239,52	1,98	54741,12	8216,55	8187,03	20,92
10	55239,53	1,10	54741,13	8216,55	8187,03	20,92
11	55236,57	0,96	54738,17	8216,11	8187,03	20,48
12	55236,52	0,89	54738,12	8216,10	8187,03	20,47