Оценка потенциальных возможностей имитационного моделирования при прогнозировании хода и исхода боевых действий с применением методов теории возможностей

ВЕСТНИК 2016

Сложность отечественных систем вооружения и военной техники, высокий темп ведения боевых действий определяют высокую сложность задачи разработки математических моделей вооружённого противоборства. Особенно сложно моделировать процессы, протекающие в условиях неопределённости. А неопределённость обстановки - постоянный фактор, сопутствующий планированию и ведению боевых действий.

При проведении тактических расчётов на основе существующих методик эффективность стрельбы оценивается вероятностью поражения цели одной зенитной ракетой. А именно: эта вероятность не известна, более того, эту вероятность никто и никогда не вычислял. Вычисляется только оценка вероятности, то есть величина случайная, оцениваемая с большой относительной погрешностью, характеризуемая математическим ожиданием и дисперсией. Поэтому в ходе статистического моделирования боевых действий само значение вероятности поражения цели должно рассматриваться как случайная величина. Значение этой вероятности перед каждой реализацией должно разыгрываться по правилам статистического моделирования в соответствии с законом распределения оценки указанной вероятности. Если этого не делать, то модель боевых действий станет несостоятельной, по Колмогорову [1], что означает, прежде всего, крайне низкую достоверность результатов моделирования. Как это ни печально звучит, но большинство математических моделей, с которыми приходилось работать авторам, относится именно к типу несостоятельных.

Одной из главных проблем, возникающих при корректном учёте статистического характера оценки эффективности стрельбы данного огневого средства по данной цели в ходе статистического моделирования, является резкое снижение темпа сходимости результатов статистического моделирования при росте числа машинных реализаций. Выход из столь неприятной ситуации может быть найден на основе отказа от парадигмы вероятностного моделирования и переходе к парадигме теории возможностей [2], частными случаями которой являются аксиоматики теории возможностей и классической теории вероятностей. Предлагается методический подход, базирующийся на одном из простейших приёмов теории возможностей, позволяющий учесть статистический характер оценок эффективности своих огневых средств и мер противодействия противника и обеспечить высокую оперативность тактических расчётов с применением имитационных статистических моделей боевых действий.

Суть данного подхода заключается в следующем. На начальном этапе оцениваются границы доверительного интервала оценки эффективности стрельбы зенитными ракетами. Левая граница интервала будет в дальнейшем обозначаться как «нижний уровень» оценки эффективности зенитного ракетного огня в простых условиях. Правая граница интервала - «верхний уровень». Середине интервала будет соответствовать «средний уровень». Эффективность мер противодействия противника также оценивается по трём аналогичным уровням. Возможные пары характера оценок эффективности зенитного ракетного огня и мер противодействия противника представлены в таблице.

Путём предварительного статистического моделирования для 9 пар точечных оценок получаются 9 интервальных оценок показателей эффективности стрельбы (рис. 1).

На рисунке символами Эi- и Эi+ обозначены соответственно левая и правая границы доверительного интервала, соответствующего i-му варианту, указанному в таблице. Большое количество полученных интервальных оценок определяет целесообразность обобщения полученного статистического материала. Результатом такого обобщения стали три интервальных оценки, представленные на рис. 2. Небольшое количество интервалов, полученных после обобщения, существенно упрощает дальнейшие действия.

Таблица

Пары вариантов сравнения огневой эффективности своих войск с огневой эффективностью противника

№ варианта	Характер оценки эффективности зенитного ракетного огня в простых условиях	Характер оценки эффективности мер противодействия противника (с точки зрения противника)
1	Нижний уровень	Верхний уровень

2	Нижний уровень	Средний уровень
3	Средний уровень	Верхний уровень
4	Средний уровень	Средний уровень
5	Верхний уровень	Верхний уровень
6	Верхний уровень	Средний уровень
7	Нижний уровень	Нижний уровень
8	Средний уровень	Нижний уровень
9	Верхний уровень	Нижний уровень

После получения эталонной оценки эффективности боевых действий Э_б ^э _д ^тал на основе «медленного» статистического алгоритма с предварительным розыгрышем значений эффективности стрельбы и мер противодействия противника начинается процедура поиска единственной (точечной) оценки эффективности стрельбы зенитными ракетами в условиях противодействия. Для этого в каждой реализации выбирается значение показате _- ля эф ₊ фективности из диапазона значений [ Э в ], [ Э с ] . Закон выборки внутри данного интервала равномерный. Если получаемая в ходе моделирования оценка эффективности не превышает 5%, то соответствующий интервал A , B , C , из которого было выбрано значение оценки эффективности получает соответствующий бонус - его вес увеличивается на единицу. В итоге, каждый из интервалов A , B , C получает вес n A , n B , n C , характеризующий количество реализаций, при которых аппроксимация оценкой эффективности из данного интервала оказалась достаточно удачной.

После этого высота прямоугольников, соответствующих интервалам A , B , C (рис. 2), устанавливается пропорционально весам n_A , n_B , n_C соответственно (рис. 3). И наконец находится проекция на ось абсцисс центра масс фигуры, полученной в результате объединения прямоугольников, отображённых на рис. 3.

Использование точечных оценок позволяет получать оценки прогнозируемой эффективности принимаемых решений в течение 1-2 минут (для масштаба соединения). Использование тех же вычислительных ресурсов «медленного алгоритма» статистического моделирования требует проведения вычислений в течение нескольких суток, что, конечно же, неприемлемо в условиях военного времени.

ВЕСТНИК 2016

--- вариант JYe 1

-*- - вариант

- вариант

- вариант

- вариант

- вариант

- вариант

- вариант

Рис. 1. Интервальные оценки показателей эффективности стрельбы с учётом мер противодействия противника

ВЕСТНИК 2016

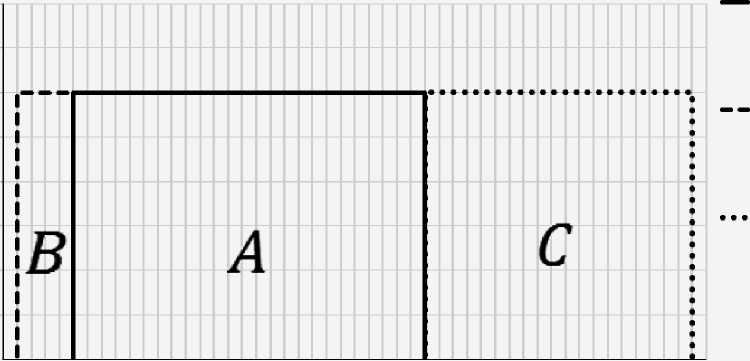
- диапазон

- диапазон оценок варьирования правых границ интервальных варьирования левых границ интервалов

- общая часть всех интервальных оценок

0,2     0,26     0,32     0,38     0,44     0,5     0,56     0,62     0,68     0,74     0,8

Показатель эффективности стрельбы с учётом мер противодействия противника

Эд

Эд*-*Эд

э^

Эс------------------------ Э£

Рис. 2. Результат обобщения интервальных оценок, представленных на рис. 1

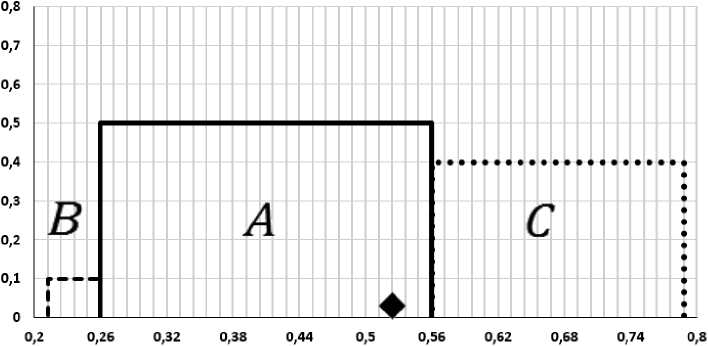
^■- общая часть всех интервальных оценок

— —- диапазон варьирования левых границ интервалов

• • • - диапазон варьирования правых границ интервальных оценок

• -♦- - наиболее точная аппроксимация оценки эффективности стрельбы

Показатель эффективности стрельбы с учётом мер противодействия противника

Эд--------------------------------- Эд эв—Эд                             эс«-------------------► Эд

Рис. 3. Формирование наиболее точной аппроксимации оценки эффективности стрельбы