Оценка применимости графовых нейронных сетей для расширения методов численной оптимизации

Графовые нейронные сети – это вид искусственных нейронных сетей, основной задачей которых является обработка данных, имеющих графовое представление.

В современном мире графовые нейронные сети находят свое основное применение в создании рекомендательных систем, решении задач по комбинаторной оптимизации, таких как оптимизация транспортного трафика и логистических маршрутов, в задачах проектирования структур в естественных науках и электронике, создании физических систем, белково-белковых взаимодействий и построении графов знаний.

Цель статьи – уточнение, систематизация и анализ существующей научной литературы в области графовых нейронных сетей и методов численной оптимизации.

В качестве источников для поиска научных трудов, использовались такие агрегаторы работ, как Elibrary, Research Gate, IEEExplore. В рамках работы рассматривались источники, опубликованные не позднее 2021 года.

Общая информация о графах

Граф – это топологическая модель, состоящая из множества вершин и множества ребер, соединяющих вершины между собой. Такие графы также принято называть неориентированные графы, поскольку у ребер таких графов не указано направление. На Рисунке 1 изображен пример такого графа.

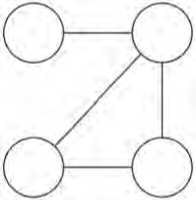
Рисунок 1. Неориентированный граф

Источник: здесь и далее рисунки выполнены автором.

Оценка применимости графовых нейронных сетей для расширения численных методов оптимизации

Каждой вершине и ребру в графе характерно свойство инцидентности.

Инцидентность – свойство, заключающееся в том, что вершина является концом ребра. На основе этого свойства можно определить свойство смежности для вершины и для ребра графа.

Вершины называются смежными , если они инцидентны одному ребру, и наоборот, если две ребра инцидентны одной вершине, то они смежные.

Ребро, инцидентное одной вершине, то есть замыкающееся на этой вершине, называется узлом .

Ребра, инцидентные одинаковым вершинам, называются кратными или параллельными .

Граф, в котором любые две вершины соединены между собой одним ребром, называется полным . На Рисунке 2 представлен пример такого графа.

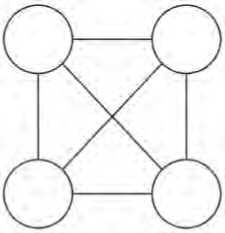
Рисунок 2. Полный граф

Если все вершины графа можно разделить на два множества таким образом, что каждое ребро соединяет вершины из разных множеств, то такой граф называется двудольным .

Любое подмножество вершин и ребер в графе называется его подграфом.

Если граф можно изобразить на плоскости так, чтобы не существовало пересечения ни одного из его ребер, то такой граф называется планарным . На Рисунке 3 представлен пример планарного графа.

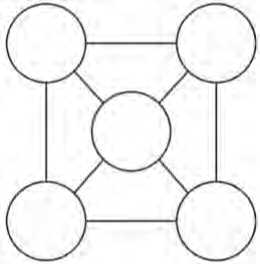
Рисунок 3. Планарный граф

Граф, в котором у каждого ребра и/или каждой вершины есть «вес» – некоторое число, которое может обозначать длину пути, его стоимость или другой определенный параметр, называется взвешенным графом .

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление», выпуск 2 за 2025 год

Аналогично граф, каждое ребро которого имеет направление, называется ориентированным графом . В таком графе для вершин определяются полустепени захода и исхода по количеству входящих и исходящих дуг соответственно. Пример взвешенного ориентированного графа представлен на Рисунке 4.

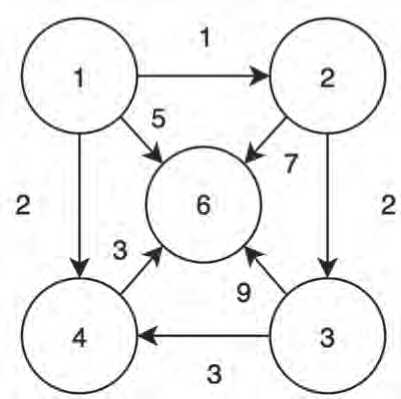
Рисунок 4. Взвешенный ориентированный граф

Вершины с нулевой полустепенью захода называются истоками , а вершины с нулевой полустепенью исхода – стоками .

Основными характеристиками графа являются матрица смежности , которая определяет связи между вершинами, и матрица инцидентности определяющая связь вершин и ребер в графе, то есть список вершин для каждого ребра, которые это ребро соединяют.

Общая информация о графовых нейронных сетях

Графовой нейронной сетью называется такая нейронная сеть, или искусственная нейронная сеть (ИНС), которая работает с данными, представленными в виде графов, то есть имеющих связанную структуру. Такие нейронные сети в основном применяются для решения трех основных типов задач:

• •    предсказание на уровне целого графа – для предсказания свойств всего графа (например, предсказать для целой молекулы ее запах; если приводить аналогию с картинками, то это задача классификации картинок);

• •    предсказание на уровне узлов – для предсказания свойств конкретного элемента в графе (например, если мы анализируем социальную сеть, то можем попытаться предсказать интересы пользователя, в случае с картинками – это задача сегментации);

• •    предсказание на уровне ребер – для предсказания свойств между двумя элементами графа (например, в анализе сцен мы можем предсказывать связь между объектами или вероятность существования определенной связи, что аналогично задаче понимания сцен).

Проблема хранения графа решается с помощью использования матрицы смежности или матрицы инцидентности, описанных выше. Поскольку матрица смежности в целом имеет разреженную структуру, то есть количество нулевых элементов значительно пре-

Оценка применимости графовых нейронных сетей для расширения численных методов оптимизации вышает количество ненулевых, и это даже в средних графах вызывает проблемы с вычислениями, предпочтительнее использовать матрицу инцидентности.

Для обработки графовой информации нейронными сетями используется механизм эмбеддинга , преобразующий исходные данные в числовые векторы. Обычно в графовых нейронных сетях эмбединг применяется к вершинам, ребрам или графу в целом в зависимости от задачи.

Также немаловажную роль играет процедура пуллинга в графовых нейронных сетях – процесс уменьшения размерности на основе окна свертки в зависимости от условия, после которого остаются либо наиболее значимые признаки, либо их агрегаты.

Таким образом, процедуры эмбеддинга и пуллинга активно используются для реализации процедуры свертки на графах, как, например, в нейронных GCN-сетях.

Для реализации свертки часто используется еще один подход, основанный на пространстве признаков, – свертка осуществляется путем агрегации объектов, находящихся только в смежных узлах или вершинах графов.

Нейронные GCN-сети

GCN (Graph Convolution Network) – графовая сверточная нейронная сеть, предназначенная для работы с графовым представлением данных, то есть имеющим связи между объектами. Такие нейронные сети хорошо решают задачи, где важно учитывать не только признаки самих объектов, но и связи с соседними объектами.

Наилучшие результаты такие нейронные сети показывают для обработки спутниковых данных, учета пространственных характеристик между объектами, распознавания образов, представленных на изображениях [1–5], данных, представленных в виде сетей [6; 7], обработки текстовой информации, поскольку нейронные сети такого типа позволяют сохранять долгосрочные зависимости и опираться на них между ключевыми словами [8].

Таким образом, GCN является отличным инструментом, подходящим для задач классификации и обработки связанных данных. Из его плюсов можно отметить следующие пункты:

• •    возможность предсказывать свойства для конкретного элемента в графе;

• •    способность предсказывать свойство между двумя элементами графа;

Но, как и другие, модель имеет ряд недостатков:

• •    разреженность матрицы смежности, что может приводить к затратам на память, так как данные не всегда сильно связаны;

• •    однородное распределение значений скрытых состояний узлов, так как различные узлы могут иметь более или менее одинаковые значения скрытых состояний, что делает их менее различимыми друг от друга, что, в свою очередь, может привести к потере информации о существенных различиях между узлами и снижению способности модели различать между ними.

Нейронные GAT-сети

В отличие от классических GC-сетей , которые вычисляют взвешенную сумму признаков соседних узлов с постоянными весами, сети GAT используют механизм внимания и самовнимания, при котором учитывается влияние не только соседних узлов, но и предыдущего состояния текущего узла, динамического определения весов на основе содержимого узлов. Это позволяет модели уделять больше внимания более важным узлам в графе.

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление», выпуск 2 за 2025 год

Сети GAT позволяют каждому узлу иметь разные веса в зависимости от контекста, что делает модель более гибкой и мощной для обработки различных графов [9; 10].

В качестве положительных качеств такой модели можно отметить:

• •    высокую точность, что достигается благодаря механизму самовнимания, который автоматически вычисляет весовые коэффициенты;

• •    самообучаемость – самостоятельное принятие решения, как выполнить заданную задачу, иногда с применением неочевидных для людей методов;

• •    эффективную фильтрацию шумов – умение сети игнорировать шумы и обрабатывать лишь необходимую информацию;

• •    адаптацию – готовность модели к возможным переменам во входных данных и продолжению эффективной работы после небольшого периода адаптации;

• •    отказоустойчивость – даже при повреждении некоторых нейронов остальные продолжают функционировать и выдавать логичные и правильные ответы, хотя точность их работы уменьшается.

Но и эта модель не лишена недостатков. В их числе:

• •    длительное обучение, что может стать проблемой при работе с крупными наборами графовых данных;

• •    проблема насыщения сети, то есть чем больше значения сигналов, тем ближе к нулю градиенты активационной функции, что мешает подбору наилучших коэффициентов;

• •    прозрачность, когда невозможно получить информацию о том, как нейросеть пришла к решению», ее можно назвать «черным ящиком»;

• •    отсутствие данных, то есть для обучения необходимо большое количество данных, и если это уникальные данные или их сложно собрать, то это может быть серьезным вызовом для разработчиков.

Методика Graph Sage

Очевидно, что при увеличении количества данных стандартная нейронная сеть и любая графовая нейронная сеть не смогут обработать все данные за адекватное количество времени. Для решения проблемы масштабируемости при работе с большими данными используют подход Graph Sage , основанный на батчировании – разбиении исходного графа на подграфы фиксированной размерности путем разбиения каждой вершины. Поскольку каждый раз генерировать новый подграф невыгодно с точки зрения вычислений, обычно берется множество точек, имеющих один общий подграф [11].

Также существует альтернатива методике Graph Sage – PinSage . В своей основе здесь используется метод случайного блуждания по графу и выбору точек с дальнейшей их приоритизацией и оценкой относительной значимости.

T-GNN нейронные сети

Одной из новейших разновидностей графовых нейронных сетей являются сети на динамических графах ( Temporal Graph Neural Network ). Идея таких сетей состоит в том, что узлы и ребра меняются со временем, а также к уже измененному графу добавляются новые временные связи и сущности.

Развитие численной оптимизации

Одной из основных частей при обучении нейронных сетей являются методы численной оптимизации, на основе которых и происходит обновление весов на каждой итера-

Оценка применимости графовых нейронных сетей для расширения численных методов оптимизации ции модели, если используется прямой ход (feed-forward) архитектуры нейронной сети, или после прохождения каждой эпохи, если используется метод обратного распространения ошибки (back-propagation).

Большая часть самых актуальных методов основана на минимизации функции потерь и прохода по вектору антиградиента для поиска локального или глобального минимума.

Также существует отдельная группа методов численной оптимизации, таких как метод имитации отжига, генетический алгоритм, которые по своей природе отличаются от градиентных методов [12].

Все методы численной оптимизации имеют один глобальный недостаток – проблему попадания в седловую точку в гиперпространстве признаков, что неизбежно приведет к недообучению модели.

Но существует ли возможность замены классических методов численной оптимизации на графовую нейронную сеть или их развития на основе таких технологий для решения существующих проблем при использовании классических подходов численной оптимизации? На данный момент существует особый класс графовых нейронных сетей, называющийся «физически информированные нейронные сети» ( PINN ). Нейронные сети, созданные на основе такого подхода, сочетают в себе физические законы и способны решать системы дифференциальных и интегральных уравнений, которые имплементируют физику какого-либо процесса. Это достигается за счет применения подхода оптимизации на основе остатков ( Residual-Based optimization ), заключающийся в том, чтобы рассматривать не ошибку предсказания, а ошибку невязки, определенную этим предсказанием [13–16].

Соответственно, из этих рассуждений можно сделать вывод, что возможность расширения численных методов оптимизации нейронными сетями существует.

Существующие проблемы

На основе изученного материала можно выделить следующие существующие проблемы графовых нейронных сетей:

• •    отсутствие достаточного количества данных для обучения моделей;

• •    сложность интерпретируемости модели, поскольку невозможно понять, каким образом нейронная сеть пришла к тому или иному решению;

• •    проблема масштабируемости, характеризующаяся сложностью оптимального разбиения большого количества графовых данных на подграфы и невозможностью обучения на огромном графе за линейное время.

В любом случае, в настоящее время существует несколько перспективных направлений развития графовых нейронных сетей:

• •    развитие интерпретируемости GNN, создание explainable AI (XAI);

• •    добавление мультимодальных данных к графу.

Прикладные области

Графовые нейронные сети могут быть применены в самых разных сферах жизни, таких как:

• •    социальные сети:

• – создание рекомендательных систем;

  – анализ сообщений;

  – детектирование сообществ;

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление», выпуск 2 за 2025 год

• •    транспорт и логистика:

  – оптимизация транспортных потоков;

  – прогнозирование ситуаций на дорогах;

• •    компьютерное зрение:

  – анализ геометрических структур;

  – сегментация изображений;

• •    научные вычисления:

  – решение комплексных математических моделей с помощью графовых нейронных сетей.

Заключение

Таким образом, в рамках данной статьи проведен анализ, систематизация и уточнение существующей научной литературы в области графовых нейронных сетей и методов численной оптимизации. В современных реалиях графовые нейронные сети являются востребованными для изучения объектами ввиду их способности обрабатывать данные, представленные в виде сложных связных структур, учитывая динамичность связей в таких данных, что позволяет делать более точные прогнозы относительно будущего поведения рассматриваемых объектов.

Также на основе результатов, полученных с помощью изучения графовых нейронных сетей и конкретно физически информированных нейронных сетей, способных решать сложные системы дифференциальных уравнений, существует возможность реализации численных методов с помощью графовых нейронных сетей и расширения возможностей этой области науки.