Оценка прочности структурированного стержня методом осреднения

Многие материалы (композиты, пенопласты, перфорированные пластины, железобетонные плиты, материалы с системой трещин и др.) и конструкции (фермы мостов, каркасы высотных зданий, наделенных междуэтажными перекрытиями) имеют структуру, близкую к периодической. Процессы в средах с периодической структурой описываются уравнениями с периодическими быстроосциллирующими коэффициентами, зависящими от малого параметра е , характеризующего относительный размер периодической ячейки. Эффективным методом исследования макроскопических и микроскопических свойств периодических структур является асимптотический метод осреднения [1], в котором решение уравнения разыскивается в виде ряда по степеням малого параметра е . Целью такого построения является получение уравнений, коэффициенты которых не являются быстроосциллирую-щими, а их решения близки в среднем к решениям исходных уравнений. Эти новые уравнения называют осредненными уравнениями, а их коэффициенты — эффективными коэффициентами материала или конструкции [1]. Отметим, что для применения метода осреднения необходимо наличие соответствующей гладкости коэффициентов уравнений.

В монографии [1] на стр. 40-49 проведено построение и подробное исследование асимптотического разложения решения задачи

(K (x/ е)и') = f (x) .    x е (0,l), и (0) = g,, и(l) = g2,

где f (x) — бесконечно дифференцируемая функция, не зависящая от е , K(x/е) = K(^), С е R — бесконечно дифференцируемая 1-пе- риодическая по ^ функция. Уравнение (1) мо- жет описывать, например, состояние равновесия линейно упругого одномерного композита длиной l всюду вне поверхностей зерен [1].

В данной работе рассматривается применение метода осреднения в задаче оценки прочности высотной башни с междуэтажными перекрытиями. За основное определяющее уравнение выбрано уравнение ( S ( x / е ) E ( x ) и'( x )) = f (x), где и (x) — величина смещения поперечного сечения башни, S(x / е) — площадь поперечного сечения с абсциссой x , f (x) — плотность равнодействующей внешних сил, действующих на сечение с абсциссой x вдоль оси башни [2]. Модуль Юнга E(x) считается постоянным, не зависящим от x. Аналогичные задачи возникают при растяжении– сжатии композитных стержней, когда структура стержня периодически меняется, причем параметр е = 2r0 /1, где 2r0 — диаметр структурной ячейки, характеризует быструю осцилляцию [3]. Обратим внимание на то, что ниже исследуется задача прочности. А потому необходимо построение асимптотических разложений решений в высших приближениях.

ПОСТАНОВКА ЗАДАЧИ

Исследуем распределение напряжений при сжатии вертикального стержня под действием собственного веса с быстроменяющейся по периодическому закону площадью поперечного сечения стержня. Такой стержень может моделировать, например, высотное здание с учетом между- этажных перекрытий. В качестве математической модели данной задачи рассмотрим уравнение

( K ( x I £ ) U ' ) = f ( x ) + g ( x I £ ) , 0 <  x <  l , (3) при краевых условиях

U (0) = U '( l ) = 0 ,            (4)

где l — высота стержня, £ = l1 n — малый параметр (при достаточно больших натуральных n , n — количество этажей), характеризующий частоту изменения жесткости K(x I £) = S (x I £) E (x) поперечного сечения стержня. Так как процедура осреднения [1] накладывает некоторые ограничения на выбор функции K(x I £) = K(^) , x I £ = e e R , то пусть K (^) является бесконечно дифференцируемой 1–периодической функцией, удовлетворяющей условию 0 < К1 < K(^) < к2, где К1 и к2 — произвольные положительные числа. Правая часть уравнения (3) отличается от правой части уравнения (1), так как f (x) описывает гладкую часть нагрузки, а g(x I £) — нагрузка, связанная со структурой ячейки (этажа). Пусть функция g(x I £) = g(^) также является дифференцируемой 1–периоди-ческой функцией, для которой {g(^)) = 0 , где угловые скобки здесь и далее означают среднее зна- чение функции по периоду {g(^)) = J g(^)de .

Кроме отличия правых частей уравнений (1) и (3) имеется и второе отличие: краевое условие (4) при x = l записано для напряжений и этим отличается от условия (2). Эти отличия обуславливают внесение изменений в метод осреднения [1]. Кроме того, в отличие от задачи (1)–(2) в задаче (3)–(4) большее значение имеет оценка напряжений, то есть производной U '( x ) решения, а не само решение U(x ) , представляющее перемещение поперечного сечения стержня.

Построим методом осреднения формальное асимптотическое разложение решения задачи (3)–(4) в высших приближениях. Предположительно целесообразно строить асимптотическое разложение до членов, содержащих £ ² включительно, чтобы с достаточной точностью можно было получить оценки напряжений, как для гладкой, так и для быстроосциллирующей составляющей решения. На конкретном примере проведем сравнение численных результатов, полученных с помощью построенного асимптотического решения с точностью до членов, содержащих £ и £ ² включительно, и аналитического точного решения.

ПОСТРОЕНИЕ

АСИМПТОТИЧЕСКОГО РЕШЕНИЯ

Учитывая линейность уравнения (3), его решение U ( x , £ ) будем разыскивать в виде

U ( x , £ ) = u ( x , £ ) + w ( x I £ ) .       (5)

Так как

( KU ' ) '= ( K ( u + w ) ‘ ) = ( Ku ' + Kw ' ) ' =

= (Ku') +(Kw') = f (x) + g(x I £) , то функцию u(x, £) — асимптотическое разложение уравнения

( Ku ') ' = f ( x )                 (6)

• — построим с помощью аналогичного [1] алгоритма, причем функция u ( x ) = u ( x , £ ) не будет зависеть от £ сингулярно; а функцию w ( x I £ ) найдем из уравнения

( Kw ' ) = g ( x I £ ) .              (7)

Произвольные постоянные в общем решении U(x, £) выберем так, чтобы выполнялись краевые условия (4). Частное решение обыкновенного дифференциального уравнения (7) можно записать в виде e                                        i

w ( e ) = J k ( y ) J g ( t ) dt + e , dr + c 0 V 0                  J

2 , (8)

где C _£ = -( K ^{- 1} )^{- 1} ( K ^{- 1}( y ) J ^r g ( t ) dt > = £ ² C i , причем C 1 не зависит от £ , C ₂ = 0 . Так как функции K ( e ) и g ( e ) являются 1-периодически-ми, то, благодаря лемме 1 из [1] и указанному выбору постоянных интегрирования C ₁ и C ₂ , построенное решение (8) оказывается 1–перио-дической функцией, причем

w (0) = 0 , w '( l ) = £ ^{- 1} w \ ( l ) = £ C 1 K ^{- 1}(0) . (9)

Перейдем к построению функции u ( x ) . Асимптотическое разложение решения уравнения (6) разыскивается в виде

E °° i d‘v ( x )

^£ N i ^{( e )} —— ,    (10)

i=i             dx где e = x I £ , функции Ni (e) — 1 периодические функции e; функция v(x) не зависит от § и имеет асимптотическое разложение

w

• v ⁽ x ) = £ ^£ P _V ⁽ x ) ,           (ii)

j =0

причем V j ( x ) не зависят от £ . Из краевых условий (4), учитывая выражение (5) и условия (9), получим следующие краевые условия для функции u ( x )

u (0) = 0 ,    u ' ( l ) = - £ C 1 K ^{- 1}(0) .     (12)

Подставим ряд (10) в левую часть уравнения (6) и краевые условия (12) и сгруппируем слагаемые при одинаковых степенях £. Будем формально считать, что переменные x и e незави- симы. Выберем функции Vj (x) и Ni (,) так, чтобы слагаемые порядка g2 и g-1 обратились в нуль, а все слагаемые более высоких порядков относительно g не зависели от ,. Так как функции Ni определяются из дифференциальных уравнений с точностью до некоторых постоянных слагаемых, то для определенности положим Ni (0) = 0 при i > 1.

Построение функций N i , i >  1 проводится по следующей рекуррентной процедуре. Для очередного по порядку значения i определим функцию T ( , ) по формулам

T ( , ) =- dK ( § )/ d g ,

T ( , ) =- K ( , ) ( dN -i /d ,+ N ₂ ) - d ( к ( , N -i ) / d , , i >  1 .                      (13)

Заметим, что функции T i ( , выражаются через функции N с меньшим индексом j <  i , причем полагается N ₀ = 1 . Определим константы h_i через средние по периоду значения функций T ( , ) , а именно положим h i =-{ T i ) , например, h 1 = 0 и h ₂ = { K ^{- 1} ) ¹ в силу 1 периодичности функции K( , ) . Затем находим очередную функцию N i ( , ) , удовлетворяющую условию N i (0) = 0 при i >  1 , как 1 периодическое решение уравнения

( K (М)' ,, ) , = T ( , ) + <  h^      (14)

Благодаря лемме 1 из [1], такое решение N i ( , ) существует и единственно.

Для построения функции v(x ) разложения (10) найдем функции V j ( x ) разложения (11), шаг за шагом решая краевые задачи следующей цепочки задач

h ₂

^{d 2 v} 0 dx ²

= f ^{( x} ) ,

h 2

^{d 2 V} q dx ²

q -1

= " E h q-j+2

j =0

dq-j+2 vj dxq-j+2 при q > 0,(15)

где n = l / g . В записи разложения (16) и уравнения (17) подразумевается, что для функций N i ( x / g ) = N i ( , ) производные вычисляются по , , а для функций и ( x ) , v i ( x ) производные вычисляются по x . Приравнивая в справедливом для любого g равенстве (17) коэффициенты при различных степенях g к нулю, получим цепочку соотношений, из которой последовательно для каждого q = 0,1,2,... найдем краевые условия для v q ( l ) . Выпишем первые три (для q = 0,1,2 ) соотношения этой цепочки

( 1 + N ;( n ) ) v 0 ( l ) : 0 ,          (18)

( 1 + NК n ) ) v ‘ ( l ) + N 2 ( n ) v 0 ( l ) : - C , K ^{- 1} ( 0 ) , (19) ( 1 + n ; ( n ) ) v ₂ ( l ) + n ; ( n v ( l ) + n ( n ) v₀(l ) = 0 . (20) Для x = l имеем

1 + dN1 / d, = K-1 (lXK-1 )-1 ^ 0 , поэтому из равенства (18) найдем краевое условие для v0 (l) и, решив краевую задачу h2 (v0)"xx = f (x),i v0(0) = 0 , v0(l) = 0, (21) где h2 =-{T2 ) = {K ) , определим функцию v0 (x). Задача (21) называется осредненной задачей нулевого порядка. Она описывает напряженное состояние в таком однородном стержне, свойства которого в некотором смысле близки эффективным свойствам исходного стержня с периодической структурой. Хотя истинные перемещения и (x) близки к средним перемещениям v0 (x), однако разность между производными точного решения и решения осредненной задачи может заметно отличаться [1]. Следовательно, для правильного определения напряжений необходимо учитывать в разложении (10) члены, содержащие g2 включительно. Решением цепочки краевых задач (15) последовательно находим функции vq (x) при всех q > 0 и этим завершается построение асимптотического разложения решения задачи (3)–(4).

АНАЛИТИЧЕСКОЕ

ТОЧНОЕ РЕШЕНИЕ

V_q (0)=0 при q >  0 , а краевые условия для v q ( l ) определяются следующим образом. Так как N i ( l / g ) = 0 , то в выражении производной асимптотического разложения (10)

to / и'(x) = v'(x) + ^2 g-1N/

1=1 V

x

g

dv¹ ( x ) dxⁱ

+ g N i

второе слагаемое под знаком суммы при x = | обращается в нуль. Подставляя в (16) разложение v(x) в ряд (11) и собирая члены при одинаковых степенях g , запишем определяющее уравнение для краевых условий vq (l) в виде и'(l) :(1 + N(n)) v0(l) +

Из уравнения (3) с учетом краевого условия

U ' ( l ) = 0 и неравенства K ( x / g ) >  0 следует равенство            x

U ' ( x ) = к ^{- 1} ( x , g ) J ( f ( z ) + g ( z / g ) ) dz .(22)

Отсюда, учитыв l ая краевое условие

U (0) = 0 , для задачи (3)-(4) получим точное решение

U ⁽ x ) = J ^{K - 1} ( y^{, g} ) J ( f ⁽ z ) + g ⁽ z / ^{g )} ) dz dy . (23)

x

Г           y

0 V               l

+ g [ ( 1 + Nn) ) цу. ) + N ₂( n ) i j ( l ) ]+ ... =- g c ; к ¹ ( 0 ) ,(17)

Для обоснования полезности сложных построений асимптотического разложения решения отметим, что хотя задача (3)–(4) имеет решение в квадратурах (23), однако непосредственный

анализ структуры этого решения (например, влияние величины малого параметра £ на значение наибольшего напряжения) сложнее анализа асимптотического разложения (10). Кроме того, точного решения может не существовать, например, в математической модели задачи, описывающей двоякопериодическую структуру конструкции. Подробное изложение преимуществ асимптотических разложений можно найти в [4]. Возможно так же, как в рассмотренном ниже примере, что уже несколько первых членов асимптотического разложения представляют точное решение.

СРАВНЕНИЕ АСИМПТОТИЧЕСКОГО И ТОЧНОГО РЕШЕНИЙ

НА КОНКРЕТНОМ ПРИМЕРЕ

Построим асимптотическое разложение решения краевой задачи

( K ( x I £ ) U ') ' = K ( x I £ ) , 0 <  x <  l , (24) U (0) = U '( l ) = 0 ,         (25)

где K ( x I £ ) = K ( 5 ) = 2 + sin ( 2 n x / £ ) . Выбор функции K( 5 ) в таком виде можно связать с выбором первых двух членов в разложении произвольной функции в ряд Фурье. Уравнение (24) является частным случаем уравнения (3), причем можно считать f (x ) = 2 , g ( x I £ ) = sin(2 nx / £ ) . В этом случае 1 периодическим решением w(x I £ ) уравнения (7) является функция

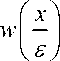
£ 2 1 fi     1 •

--- ln 1 + —Sin

4 п ²   I     2

2 . x У

^£ VJ

для которой w (0) = 0 , w '( l ) = -£ I(4 n ) . Поэтому для решения уравнения

(K (x I £) u')'= 2 , (27) краевые условия с учетом выражения (5) и условия (25) имеют вид u (0) = 0, u'(l) = £ I(4n). (28)

Функции Ni(5), i > 1 разложения (10) найдем из уравнения (14) с учетом соотношений (13). Так, для определения функции N1 уравнение (14) при i = 1 можно записать в виде d (K (dN,I d5 +1)) I d5= 0, следовательно, dN11 d^ = C11K (5) — 1. Отсюда, учитывая ра венство Ni (0) = 0,получим

^N 1 = c f

d 5

K ( 5 )

где константа c ₁ вычисляется из условия 1 периодичности функции N ₁ следующим образом. Так как справедливо равенство (dN 1 I d ^ = N 1 (1) — N 1 (0) = 0 и равенство

(dN1I d^ = c (k-1 (5 )}—1 , то c 1 = ^K ^

d ^

0 2 + sin(2 n5 )

—1

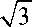
Окончательно для функции N ₁ получим выра жение _{z x} ,-C

N1 (5 ) = V3 f—d4——5

(29)            0 ^{2 + Sin ( 2 n5} )

-

.

Заметим, что так определенная функция N 1 ( 5 ) является 1 периодической, причем N 1 ( n ) = N । ( 0 ) . Для определения функции N ₂ ( 5 ) сначала, пользуясь равенствами (13), (14) и учитывая 1 периодичность функций K ( 5 ) и N i ( 5 ) , находим функцию

T ( 5 ) = —⁷³— 5 K ( 5 ) N 1 )

и вычисляем

среднее по периоду \ Т ₂/ = — V3 . Затем из уравнения (14) имеем

KdN21 d5 = f (T2 — (T2))d5 = — KN1 + c2, где константа c2 вычисляется аналогично вычислению константы c1 из условия 1 периодичности функции N2 следующим образом. Так как (dN2I d5 = c2 (k — (N1) = N2 (1) — N2 (0) = (0 то c2 = {N1)I(k^ = c1 (N1) = V3{N,). Наконец, учитывая равенство (29) и условие N2 (0) = 0 , получим для 1 периодической функции N2 выражение

N 2 ( 5 ) = f dN 2 d 5 = f (V3( N 1) I K — N 1 ) d 5 .(30) 0 d ⁵ 0

Функции N i ( 5 ) при i >  2 находятся аналогично из рекуррентных соотношений (13)–(14), но их вычисление для решения задачи (24)–(25) не требуется, потому что в этом случае, как будет показано ниже, ряд (10) не содержит членов с £ ⁱ при i >  3 .

Для определения функции v ( x ) разложения (10) находим функции V j ( x ) разложения (11), решая последовательно краевые задачи цепочки задач (15). Краевая задача (21) при h 2 ={ K ') ¹ = V3 и f ( x ) = 2 имеет решение V ₀ ( x ) = x ( x — 2 1 ) IV3 . Пользуясь представлениями (29), (30) вычислим значения выражений 1 + N ‘ ( 11 £ ) = V3I2 , N ‘ ( 11 £ ) = V3 { N 1 >  I2 и с учетом условий (28), (17) и (19) для определения функции V 1 ( x ) запишем краевую задачу

V3 ( V 1 )' x, = 0 - v 1 ⁽°) = « •

V1'(l) = 2(1I4n—(N1»Л/3 , решением которой является многочлен первой степени v1 (x) = 2(1/4п — NN। ^) x/ V3 . Следовательно, благодаря соотношению (20), для нахождения функций vq краевая задача (15) при q > 2 принимает простой вид V3v^'(x) = 0 , vq (0) = vq (l) = 0 , решением которой является vq ( x ) = 0 для любого q > 2 . Окончательно для функции v (x) находим разложение (11) в виде многочлена второй степени относительно x

K

x — l + 8 1 — cos 4п V

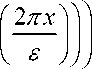
v ( x ) = v0 ( x ) + 8v1 ( x ) =

x (x — 2l)

+ 8~^

4n

—

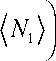
x

.

Используя выражение (31) в разложении (10) для производной решения и ( x ) краевой задачи (27)–(28) получим представление

и'(x) = 2(x — l + 8/(4n))/K(x/8). (32)

Если в разложении (10) пренебречь членами, содержащими 8 во второй и более степени, то получим приближенное выражение производной

и'(x)«(v (x) + eN1 (x / 8) v'(x)) =

которое полностью совпадает с асимптотическим разложением (34).

Полученные выражения (33), (35) для напряжений в стержне со структурой ( n –этажной башне) сравним с выражением напряжения с т ( x ) в однородном стержне с постоянной площадью S ₀ поперечного сечения [5, 6]

с ( x ) — x — l . (36)

Заметим, что формулу (36) для с ( x ) — U ' ( x ) можно получить, вычислив производную точного аналитического решения задачи (24)-(25) при K ( x / 8 ) — S 0 — const . Эту же формулу (36) можно получить для производной с ( x ) — v 0 ( x ) решения v 0 ( x ) осред-ненной задачи нулевого порядка (21), то есть для напряжений в эквивалентном однородном стержне, при h ₂ — ( K ^{— 1} )^{— 1} — 2 , f ( x ) — K , где K — K ( x / 8 ) — 2 , причем в этом случае производная U ' ( x ) асимптотического разложения решения U ( x ) задачи (24)-(25) совпадает с v ‘ ( x ) , то есть U ' ( x ) — v ‘ ( x ) — с т ( x ) — x — l .

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ РАСЧЕТОВ

2 L . 8 ] , — — x — l +--+ 28

K V      4n J

N 1

v

—

(Ni))

Интересно отметить, что приближенное с точностью до 8 включительно выражение (33) оказалось сложнее точного представления (32). Согласно (26) функция w ( x / 8 ) « O ( 8 ² ) , поэтому приближенное с точностью до 8 разложение производной U '( x ) решения задачи (24)-(25) дается по-прежнему выражением (33), а асимптотическое разложение производной решения с учетом всех членов записывается формулой

U'( x ) — и'( x ) + w'( x ) —

2 f , 8 ) 8 cos (2nx / 8)

— — x — l +------------- ("34У

K V       4 n J 2 n      K ’ ^{( )}

где для функций и ' ( x ) и w ' ( x ) использованы представления (32) и (26) соответственно.

Теперь найдем точное решение задачи (24)– (25). Пользуясь равенством (22), получим для производной точного решения выражение

U' (x) — K—1 j (2 + sin (2nx / 8)) dx —

l

Приведем численное сравнение полученных результатов для стержня высотой l _— 1 . На рис. 1-3 для различных 8 ( 8 — 1/2 ,1/5 и 1/50) построены кривые 1–3 зависимости напряжения от высоты x поперечного сечения стержня, вычисленные по формулам (33), (35) и (36) соответственно. С уменьшением 8 значения напряжений, вычисленные по формулам (33) и (35), почти совпадают, поэтому кривые 1 и 2 на рисунке 3 неразличимы.

На рис. 4 приведены графики трех первых волн зависимости напряжения U ' ( x ) от высоты x поперечного сечения стержня для 8 _— 1/20 , вычисленные по формуле (34): при 0 <  x <  8 — волна 1 (нижняя), при 8 <  x — x 1 <  2 8 — волна 2 (средняя) и при 2 8 <  x — x ₂ <  3 8 — волна 3 (верхняя). Существенно, что напряжение (34) в структурированном стержне представлено алгебраической суммой гладкой и быстроосциллирующей частей, причем последняя, как видно из рис. 4, является почтипериодической функцией. Именно это обстоятельство позволяет сформулировать периодические граничные условия задачи (3) для структурной ячейки [7], опираясь только на гладкую часть решения [4] в точке x _— 0 • Периодические граничные условия ставятся как на саму функцию U ( x ) , так и на функцию напряжения

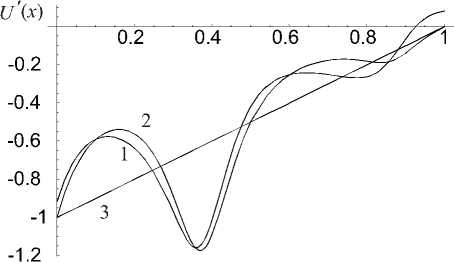
Рис. 1. Зависимость напряжения от высоты x для £ — 1/2

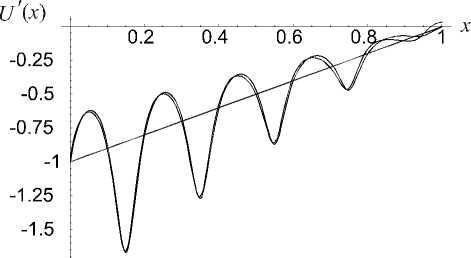
Рис. 2. Зависимость напряжения от высоты x для £ — 1/5

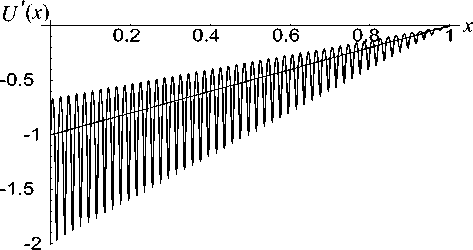
Рис. 3. Зависимость напряжения от высоты x для £ — 1/50

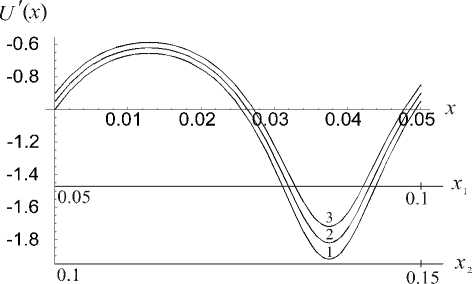
Рис. 4. Три первых волны зависимости напряжения U '( х ) для £ = 1/20

5ЛА^

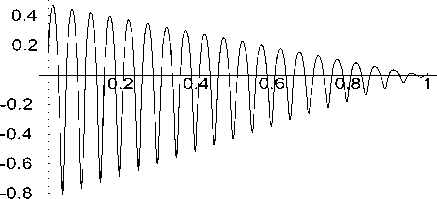
Рис. 5. Вклад в зависимость U '( х ) членов,

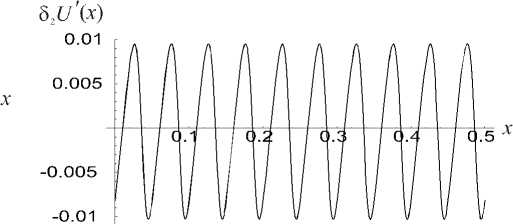
Рис. 6. Вклад в зависимость U '( х 1 членов,

содержащих только £ ( ^{£ —} 20 ).

содержащих только £ ² ( ^{£ —} 20 ).

Таблица. Концентрация напряжений в структурированном стержне.

£	x	U ( х )	° ( х )	U ( х ) / о ( х )
1/2	0,375	- 1,170	-0,625	1,87
1/5	0,15	- 1,668	-0,85	1,96
1/10	0,075	- 1,834	-0,925	1,983
1/20	0,0375	- 1,917	-0,9625	1,992
1/50	0,015	- 1,967	-0,985	1,997
1/100	0,0075	- 1,983	-0,9925	1,998

U '( х ) . Задача (3) с периодическими граничными условиями позволяет получить наихудшую оценку на коэффициент концентрации напряжения за счет структуры.

На рис. 5 с учетом выражений (5), (10) и (26) дан график вклада в зависимость напряжения U '( х ) членов, содержащих только £ в первой степени, то есть построен график функции

5 1 U ' ( х ) — £ [ N 1 ( ^ )v ' ( х ) ] . На рис. 6показан график функции

52U(х) — £ |_N2 (^)v (х) -ln(1+sin(2пх/£)/2)/2nJ, содержащей только члены с £2, которая является 1–периодической функцией благодаря 1–периодичности функции N2 (^) и равенству v"(x) = 2/V3 .

В таблице для различных £ приведены значения напряжения U ' ( x ) в структурированном стержне высотой l = 1 и значения напряжения с т ( x ) в однородном стержне, вычисленные при x = 3 £ /4 . В последнем столбце таблицы дан коэффициент концентрации напряжения за счет структуры — значение отношения U ' ( x ) / с т ( x ) . Из выражений (35) и (36) находим, что для любых £ справедливо неравенство U ( x ) / с ( x ) <  2/ K ( x / £ ) = 2/ ( 2 + sin ( 2 n x / £ ) ) <  2 . При этом равенство достигается в n = l / £ точках x = x_k = £ k - £ /4 , где k = 1,2,..., n . Следовательно при £ ^ 0 в этих n ^ да различных внутренних точках стержня коэффициент концентрации напряжения за счет структуры стремится к двум, что согласуется с данными последнего столбца таблицы.

ВЫВОДЫ

Расчеты показывают, что напряжения в структурированном стержне могут почти вдвое превышать напряжения в эквивалентном однородном стержне, распределение максимальных напряжений в осредненной задаче позволяет поставить периодическую задачу для наиболее нагруженной ячейки композита.