Оценка производительности приложений параллельной обработки изображений
Автор: Волотовский Сергей Геннадьевич, Казанский Николай Львович, Попов Сергей Борисович, Серафимович Павел Григорьевич
Журнал: Компьютерная оптика @computer-optics
Рубрика: Обработка изображений: Восстановление изображений, выявление признаков, распознавание образов
Статья в выпуске: 4 т.34, 2010 года.
Бесплатный доступ
Предложен метод оценки производительности приложений, предназначенных для параллельной обработки изображений. Данный метод базируется на сочетании аналитического подхода и использования результатов вычислительных экспериментов. Аналитическая составляющая метода представлена в характерном для типовых задач параллельной обработки изображений виде и параметрически учитывает три вида вычислительных затрат: использование процессора, межпроцессорные пересылки данных, операции ввода/вывода. Результаты вычислительных экспериментов использованы для оценки неизвестных параметров аналитической модели, что позволяет эффективным образом строить новые или модифицировать существующие алгоритмы параллельной обработки изображений.
Параллельные вычисления, обработка изображений, масштабируемость параллельных приложений
Короткий адрес: https://sciup.org/14058978
IDR: 14058978
Текст научной статьи Оценка производительности приложений параллельной обработки изображений
Создание эффективных параллельных приложений предполагает умение предсказывать зависимость их производительности от алгоритма, внутренних параметров, архитектуры вычислительной системы. Для этой цели используются как аналитические подходы, так и результаты вычислительных экспериментов. Использование аналитики позволяет наиболее быстро получать требуемые результаты . Однако для многих сложных параллельных приложений затруднительно создать адекватную аналитическую модель оценки производительности. С другой стороны, проведение вычислительных экспериментов иногда требует затрат недопустимо большого времени [1].
Часто основное внимание при оценке производительности параллельного приложения уделяется той его компоненте, которая связана непосредственно с вычислениями на центральном процессоре. В этом случае, однако, исключение из анализа других важных компонентов, например, обмена данными между процессорами или операций ввода/вывода, может исказить правильность полученных результатов. Доля влияния каждого из компонентов параллельного приложения на производительность системы может зависеть от специфики самого приложения, архитектуры вычислительного комплекса, его поколения [2].
Например, в современных суперкомпьютерах и кластерах всё более увеличивается разрыв между производительностью центрального процессора и устройств ввода/вывода. Производительность центрального процессора растёт значительно быстрее. Чтобы оптимизировать операции ввода/вывода, необходимо уметь точно оценивать их вклад в общую работу системы. Учитывая иерархичность архитектуры современных средств работы с памятью, это является сложной задачей. Архитектура памяти обычно состоит из регистров центрального процессора, кэшей разных уровней, оперативной и дисковой памяти. Скорость обмена между оперативной и дисковой памятью минимальна в этой иерархии. Поэтому оптимизация операций этого звена, как правило, наиболее важна [3].
С ростом объёма регистрируемой фото- и видеоинформации возрастает важность эффективной обработки крупноформатных изображений [4-6]. Для хранения крупноформатных изображений обычно используются файловые хранилища с возможностью параллельного чтения/записи. Возникающие при обработке изображения промежуточные результаты можно сохранять в локальной файловой системе (ЛФС) вычислительного узла или использовать сетевую файловую систему (СФС), например NFS (Network File System) [7]. Каждый из этих подходов имеет свои преимущества и недостатки .
Использование СФС является единственным способом сохранения промежуточных данных при использовании бездисковых класт еров. Преимуществом СФС является простота использования, при которой достигается доступность всего файла, размещённого в СФС, всем вычислительным узлам. Недостатком СФС является низкая по сравнению с ЛФС скорость чтения/записи. При активном использовании СФС также необходимо, чтобы файловые операции не замедляли операции пересылки данных межд у процессорами. Поэтому для файловых операций в СФС желат ельно организовать отдельную коммуникационную сеть межд у вычислительными узлами.
Использование ЛФС обеспечивает высокую скорость чтения/записи. Н едостатком ЛФС для разработчика параллельного приложения является необходимость обеспечивать вычислительным узлам доступ к требуемым фрагментам используемого файла. Часто это приводит к дублированию частей файла на вычислительных узлах. Таким образом, по сравнению с СФС возрастает объём необходимого дискового пространства. Также использование ЛФС за- трудняет организацию корректного завершения программы, при котором не наруш алась бы целостность сохранённых данных. Эта проблема особенно актуальна при использовании менеджера ресурсов кластера, например, Torque [8].
Аналитическая модель
В качестве примера использования покомпонентного подхода, предлагаемого для оценки производительности приложений параллельной обработки изображений, рассмотрим задач у параллельной обработки изображения скользящим окном [9, 10]. Отсчёты обработанного изображения являются результатом свёртки соседних значений каждого отсчёта со значениями маски. Таким образом, при размере маски m×m для каждого отсчёта выполняется m2 операций умножения-сложения. Буд ем полагать, что m нечётно. Определим время работы процессора, треб уемое для выполнения одной операции умножения-сложения, как tCPU. Тогда один проход по изображению скользящим окном треб ует времени при последовательной обработке m2 tCPU n2. Здесь полагается, что изображение, как и маска, является
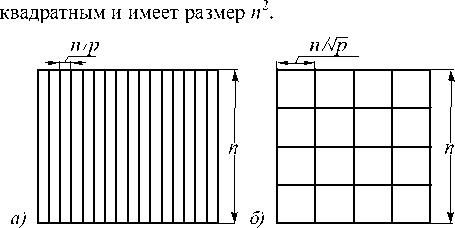
Рис. 1. Примеры распределения фрагментов изображения между процессорами:
одномерная сетка (а) и двумерная сетка (б)
Параллельная обработка изображения предполагает распределение вычислений по заданному количеству процессоров p . На рис. 1 показаны два возможных способа такого распределения: разделение изображения на полосы (рис. 1 а ) и на квадратные блоки (рис. 1 б ). Оценим отношение затрат на пересылку данных межд у процессорами к вычислительным затратам для обоих этих способов. Обозначим этот параметр как CCR (communication-to-computation ratio) [11]. При разбиении изображения по одномерной сетке (рис. 1 а ) каждый процессор обрабатывает фрагмент изображения размером n 2/ p отсчётов. Для обработки граничных отсчётов каждому процессору потребуются данные от соседних процессоров. Данная пересылка содержит n ( m – 1) отсчётов. Если не учитывать затраты на чтение/запись обрабатываемого изображения, то CCR равно 2 ( m – 1) p/n .
При разбиении изображения по двумерной сетке (рис. 1 б ) каждый процессор также обрабатывает фрагмент изображения размером n2 / p отсчётов. В данном случае пересылаются отсчёты, которые расположены по периметру каждого некраевого фрагмента изображения. Данная пересылка содержит
4( m - 1) n / 4"p отсчётов. Без учёта затрат на чте-ние/запись обрабатываемого изображения CCR в данном случае равно (4( m - 1) -Jp ) / n .
Определим время работы параллельного алгоритма обработки изображения скользящим окном при разбиении изображения по одномерной сетке. Процесс обработки в общем случае состоит из 3 шагов:
-
а) чтение/запись изображения,
-
б) пересылка данны х межд у процессорами,
-
в) обработка фрагмента изображения скользящим окном.
Таким образом, время выполнения параллельного алгоритма обработки изображения скользящим окном записывается в следующем виде:
km 2 n 2
Tp = tCPU + p (1)
+k ( m-1)( tL + tBn ) + ( toe + tRw ( n 7 p )) , где n x n - размер изображения, m x m - размер скользящего окна, k – количество проходов по изображению скользящим окном, p – количество процессоров, tCPU – время выполнения базовой операции процессором, tL – латентность межпроцессорных соединений, tB – ширина пропускания полосы межпроцессорных соединений, tOC – время откры-тия/закрытия файла, tRW – ширина полосы передачи данных при чтении/записи файла.
Функция накладных расходов, которая определяет время, потраченное всеми процессорами на «неполезную работу», в данном случае записывается в виде:
T o = kp ( m - 1 )( t L. + tBn ) + pt o C + tRWn 2 . (2)
Параметры, которые содержатся в аналитической модели (1), позволяют охватить широкий класс алгоритмов обработки изображений скользящим окном. Например, параметр m позволяет определить несколько видов операций:
-
1) точечные операции ( m = 1),
-
2) окрестные операции (1 < m < n ),
-
3) глобальные операции ( m = n ) [12].
Результаты экспериментов
Для определения значений параметров в формуле (1), соответствующих конкретной вычислительной системе, было проведено моделирование на кластере, содержащем 28 четырёхядерных процессора ( p = 28 × 4 = 112), с пиковой мощностью около 1 Тфлопс.
Для определения значения t CPU фиксировались остальные (кроме n ) значения параметров в первом слагаемом формулы (1). При запуске тестовой программы обработки изображения скользящим окном замерялось время, затрачиваемое непосредственно на обработку, т.е. без учёта затрат на чтение/запись файла и на п ересылку данных межд у процессорами. Размер отсчёта изображения равен одному байт у.
На рис. 2а показаны затраты на обработку в виде зависимости времени от размера изображения. Точ- ки на графике данной зависимости аппроксимируются линейной зависимостью. Исходя из этой ап-
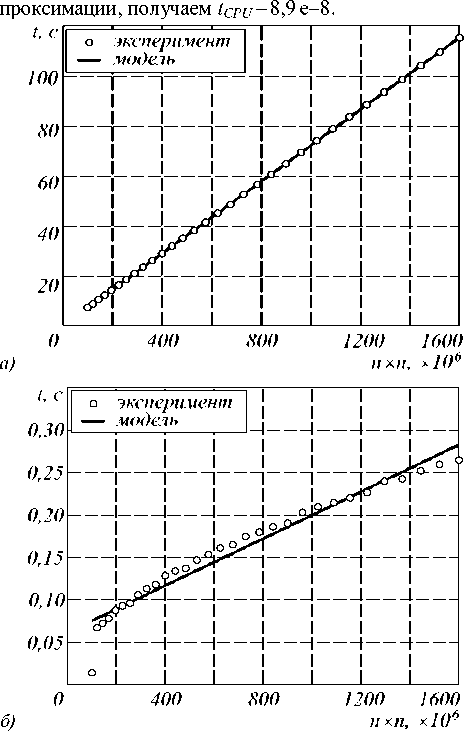
Рис. 2. Линейные аппроксимации зависимости времени выполнения фрагментов тестовой программы (секунд) от размера изображения (млн. отсчётов) для обработки изображения скользящим окном (а) и операций чтения/записи изображения (б)
Аналогично рассчитываем в ремя, которое затрачивается на чтение изображения (рис. 2 б ). В исследуемой реализации алгоритма скользящего окна фрагменты обрабатываемого изображения размещаются локально на каждом вычислительном узле. Также, используя линейную аппроксимацию, получаем t RW = 1,5 e–8 и t OC =6,1 e–8.
На используемом кластере установлены коммуникационные сети двух спецификаций: Gigabit Ethernet и InfiniBand. На основании стандартных тестов для этих сетей были получены значения t L = 46,85 e–6, t B =9,5 e–6 для Gigabit Ethernet и t L = 1,25 e–6, t B = 8,9 e–7 для InfiniBand. В дальнейшем анализе использованы параметры сети InfiniBand, если не оговорено другое.
Введённое выше понятие CCR удобно использовать для оценки вклада каждого из компонентов вычислительной системы в выполненную работу по параллельной обработке изображения. Определим понятие коммуникации в CCR как совокупны е операции по чтению/записи обрабатываемого изобра- жения и операции пересылки данных межд у процессорами. Тогда выражение для CCR запишется в виде
CCR =
P ( m - 1)( tL + tBn )
2_.2 + tCPU m n ptOC + tRWn
+ 2...2
ktCPU m n
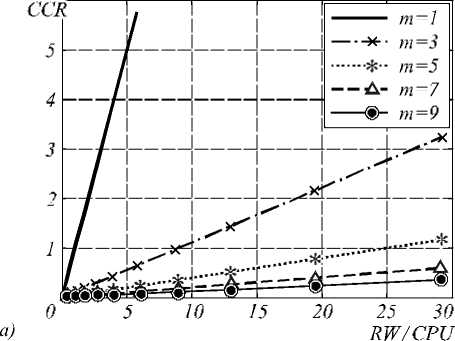
На рис. 3 а показана зависимость CCR от отношения t RW / t CPU для операций чтения изображения при различных размерах маски. Здесь фиксировалось значение t CPU = 8,9 e–8. Можно интерпретировать уменьшение отношения t RW / t CPU при фиксированном t CPU как использование более быстрых дисковых накопителей, а его увеличение как, например, использование сетевой файловой системы NFS вместо локального размещения фрагментов изображения на каждом вычислительном узле. С другой стороны, уменьшение отношения t RW / t CPU при фиксированном t RW можно интерпретировать как использование более быстрых процессоров.
0 20 40 60 80 100 120 140
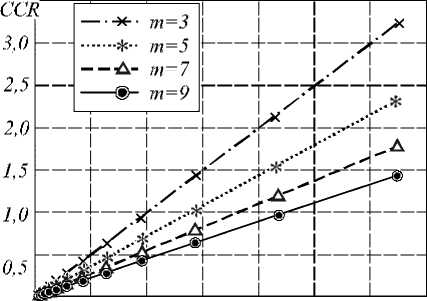
Рис. 3. Зависимость CCR для операций чтения файла от отношения tRW /tCPU (а), для операций пересылки от отношения tB /tCPU (б)
На рис. 3 б показана зависимость CCR от отношения t B / t CPU для операций чтения изображения при различны х размерах маски. Здесь также фиксировалось значение t CPU = 8,9 e–8. Можно интерпретировать уменьшение отношения t B / t CPU при фиксированном t CPU как использование более быстрых ком-
-
б)
муникационных сетей. Так, переход на графике от значения отношения t B / t CPU , равного ~100, к значению, равному ~10, означает переход от сети Gigabit Ethernet к сети InfiniBand.
Анализ масштабируемости приложения
Для дальнейшего анализа определим эффективность задачи E как отношение полученного ускорения к количеств у процессоров. Функция изоэффективности [1] определяет скорость, с которой должен расти размер задачи с ростом количества процессоров, чтобы поддерживать фиксированную эффективность. Рассматриваемая вычислительная задача считается хорошо масштабируемой, если размер изображения должен расти линейно как функц ия от количества процессоров.
В нашем случае ф ункция изоэффективности записывается в виде tCPUm 2 n 2 = E-^TO (n, P) . (4) 1 - E
Чтобы получить зависимость размера изображения от количества процессоров, необходимо решить квадратичное по переменной n уравнение.
На рис. 4 показаны фун кции изоэффективности для нескольких значений эффективности. Отметим, что накладные расходы в виде затрат на п ересылку данных и чтение/запись изображения не повлияли на линейный характер ф ункции изоэффективности. На рис. 4 а размер маски равен 3. На рис. 4 б показана ф ункция изоэффективности для различных значений размера маски. Значение эффективности на рис. 4 б принято равным 70%.
Функция изоэффективности позволяет выполнять анализ масштабируемости параллельной задачи в зависимости от различных параметров. Например, из анализа рис. 4 б след ует, что с ростом размера маски при фиксированном размере задачи треб уется большее количество процессоров, чтобы поддерживать заданное значение эффективности. Таким образом, с увеличением размера маски масштабируемость задачи улучшается.
Заключение
Проведённый покомпонентный анализ вычислительной системы позволил получить функции ускорения, накладных расходов, масштабируемости и исследовать их зависимость от различных параметров, например, от размера окна обработки, количества итераций, доли операций ввода/вывода в общем количестве вычислений .
Сочетание аналитического подхода с использованием результатов вычислительных экспериментов, с одной стороны, позволяет сократить время, затрачиваемое на вычислительные эксперименты при анализе эффективности сложных приложений параллельной обработки изображений. С другой стороны, аналитическ ая составляющая модели позволяет эффективным образом строить новые или модифицировать существующие алгоритмы параллельной обработки изображений.
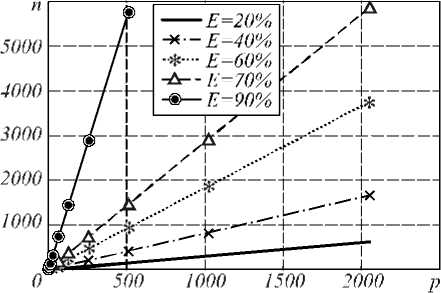
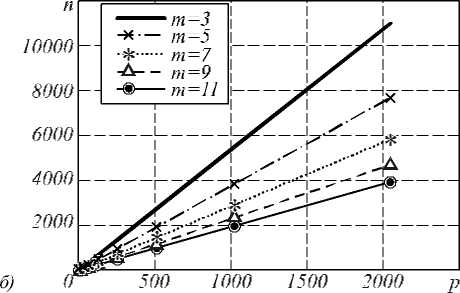
Рис. 4. Функция изоэффективности для m=3 (a) различных значений размера маски m при E=70% (б)
Работа выполнена при финансовой поддержке Программы фундаментальных исследований Президиума РАН «Проблемы создания национальной научной распределённой информационно-вычислительной среды на основе развития GRID технологий и современных телекоммуникационных сетей», грантов РФФИ № 10-07-00553, 09-07-00269 и гранта Президента РФ № НШ-7414.2010.9, а также Федеральной целевой программы «Научные и научно-педагогические кадры инновационной России» на 2009-2013 годы.


