Оценка радиолокационных характеристик мишени - «большой корабельный щит»

При анализе результатов испытаний ракет возникла необходимость в оценке радиолокационных характеристик мишени – «большого корабельного щита пр. 436-бис» (БКЩ) на конечном участке полета ракеты, а именно измерение эффективной отражающей поверхности (ЭПР) и получение процесса флюктуации кажущегося центра отражения (КЦО) в пределах продольной оси мишени. Аналогичные измерения параметров мишени были проведены более 30 лет назад в воинской части, эксплуатирующей данную мишень, но в настоящее время воинская часть этими результатами не располагает.1

Проведение дополнительных облетов мишени самолетом-лабораторией является весьма дорогостоящим мероприятием. Поэтому для оценки радиолокационных характеристик мишени целесообразнее провести моделирование отражения радиоволн от мишени в сантиметровом диапазоне длин волн.

Оценка радиолокационных характеристик мишени приведена в научно-техническом отчете [1].

Но в данном отчете результаты моделирования приведены только для участков полета ракеты в несколько десятков длин волн, чего явно недостаточно для решения поставленной задачи. Получение результатов работы этой модели для всего конечного участка полета ракеты затруднительно, так как отчет не содержит подробного описания модели, а также не приведена и сама модель.2

В связи с этим предложена простая и удобная (в плане вычислительных затрат) модель перемещения КЦО мишени, которая в отличие от указанного моделирования [1] не учитывает сферичности фронта отраженной волны в ближней зоне наблюдения мишени.

Корректность предложенной модели подтверждена путем сравнения результатов расчета и результатов натурной работы с реальной ракетой по БКЩ. Сравнение результатов расчета и натурной работы выполнено по имеющимся в телеметрической информации параметрам ω а и β а – угловой скорости и угловому положению по азимуту строительной оси антенны радиолокационной сис-

темы наведения (РСН) ракеты. Для преобразования расчетного положения КЦО мишени в ω а и β а использована упрощенная модель системы угловой автоматики (СУА) РСН.

Согласно данным в [2] мишень БКЩ представляет собой надводную плавающую платформу с расположенными на ней в особом порядке 11 отражающими элементами – уголковыми отражателями (УО) с разными высотами расположения и разными значениями ЭПР.

Как сказано в [3], такой многоточечный объект формирует суммарный кажущийся центр отражения. По мере подлета к мишени изменяется характер ее отражающей способности – ЭПР и смещается положение КЦО. Временные флюктуации угла прихода отраженного от БКЩ сигнала называют угловым шумом или угловым мерцанием объекта. Это явление приводит к угловой ошибке при сопровождении радиолокационной системой наведения ракеты.

Исходными данными для расчета являются телеметрические параметры, полученные с натурной работы ракетой по мишени БКЩ: координаты ракеты – Х р , Z p , Y p , проекции скорости ракеты на оси х и z – V x , V z и координаты цели – Х ц , Z ц . РСН ракеты работает в многочастотном режиме автосопровождения (цикличный перебор из k частот (массив длин волн λ [ k ]) с фиксированным шагом) при обработке s подпачек из n импульсов. Темп считывания исходных данных и шаг расчета соответствуют периоду повторения импульсов в РСН.

Также в качестве исходных данных использованы координаты расположения УО на мишени (массивы трехмерных координат X [ i ], Y [ i ], Z [ i ]) и ЭПР каждого из УО (массив σ [ i ]), где i = 0…11.

На рис. 1 показана структурная схема программы расчета углового положения, скорости перемещения и ЭПР КЦО мишени.

Принимается, что БКЩ расположен перпендикулярно к направлению подлета ракеты, вследствие чего ось Х БКЩ сонаправлена с осью Z р (рис. 2).

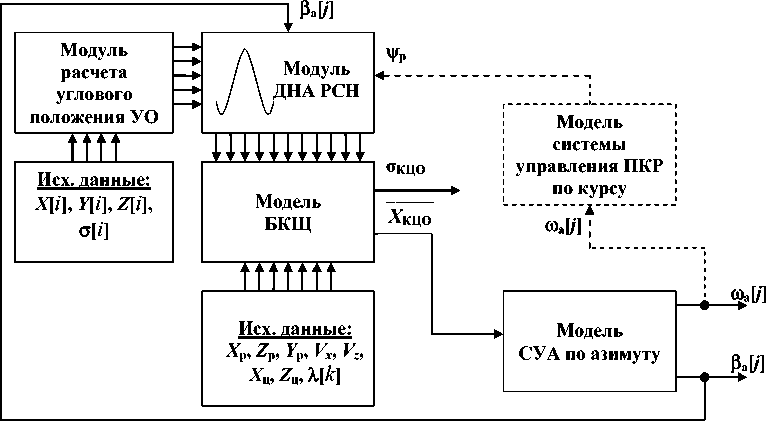
Рис. 1. Структурная схема программы расчета характеристик БКЩ

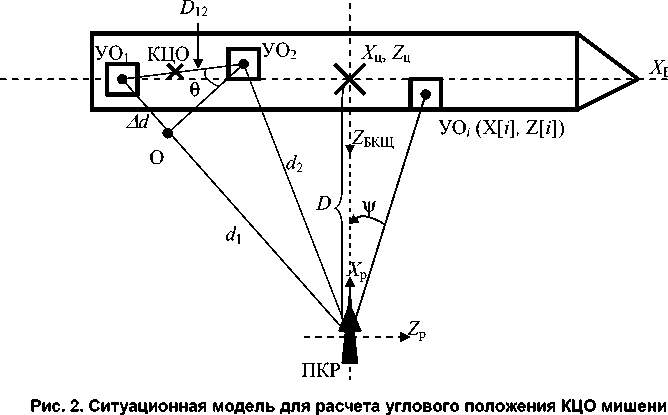
Координаты центра БКЩ совмещены с координатами цели Х _ц , Z _ц .

Исходные данные X [ i ], Y [ i ], Z [ i ] поступают в модуль, выполняющий расчет углового положения уголкового отражателя БКЩ. Угловое положение i -го УО может быть определено как

4) набег фазы сигнала РСН (в рад) на интервале A d

4 nA d ^ф = X [ к ] ’

V _УО [ i ] = - a tan

X [ i ] D

5) коэффициент m отношения откорректированных по (3) ЭПР УО 1 и УО 2

где X [ i ] – координата i -го уголкового отражателя по продольной оси БКЩ; D – текущая дальность от ракеты до центра БКЩ ( Х _ц , Z _ц ).

Модуль ДНА РСН содержит аппроксимирующую функцию вида

m =

o [1]

\ o[2] *

9а (V) =

sin( u v ) u V

• 6)    суммарная ЭПР УО 1 и УО 2 (ЭПР кажущегося центра отражения от УО 1 и УО 2 )

° КЦО = 0 (1] * + O [2] * + 2V o [1J * o [2J * cos ф ;

• 7)    расстояние между УО 1 и УО 2

D 12 = V ( X [1] - X [2] ) 2 + ( У [1] - Л 2] ) 2 + ( Z [1] - Z [2] ) ²;

где u = 20, v = 2 – параметры аппроксимации ДНА; V (в рад, см. рис. 2) является аргументом функции диаграммы направленности антенны, соответствующим угловому положению i -го уголкового отражателя БКЩ из (1) и текущему угловому положению строительной оси антенны Р а [ /' ] для j -й подпачки ( j = 1… s ), и может быть определен как

V = V УО ^[ i ^] -Р а ^[ j ^].

В соответствии с (2) ширина ДНА по уровню половинной мощности составляет 8 ° .

С помощью функции, аппроксимирующей диаграмму направленности антенны РСН, в модуле ДНА РСН производится корректировка значения ЭПР каждого уголкового отражателя БКЩ.

Корректировка ЭПР i -го уголкового отражателя ( о [ i ]) осуществляется следующим образом:

о [ i ] * = о [ i ] 6 а ( у ).                                (3)

Расчет [3–5] углового положения кажущегося центра отражения БКЩ ( Х КЦО , Y КЦО , Z КЦО ) осуществляется для текущего положения ракеты при излучении РСН одного импульса с длиной волны Л [ k ] ( к - номер рабочей частоты РСН) путем нахождения углового положения КЦО, образованного первыми двумя отражателями (см. рис. 2, УО 1 и УО 2 ), а затем последовательного нахождения углового положения КЦО, образованного следующим уголковым отражателем (УО i ) и кажущимся центром отражения, определенным ранее. Процесс продолжается до достижения последнего УО 11 .

Соотношения для расчета КЦО для БКЩ в соответствии с ситуационной моделью (см. рис. 2) приведены ниже:

• 1)    дальность от ракеты до первого уголкового отражателя (УО ₁ )

d i = / X ц - z [1] - X р ) 2 + (Л 1] - У ) 2 + ( z ц + X [1] - z р ) 2 ;

• 2)    дальность от ракеты до второго уголкового отражателя (УО 2 )

d 2 = ^( X ц - Z [2] - X р ) ² + ( Л 2] - У ) ² + ( Z ц + X 2] - Z р ) ²;

• 3)    разность дальностей от ПКР до первых двух отражателей

A d = d ₂ - d 1 ;

8) угол 6 (в рад)

6 = arcsin

Ad

^D 12

9) величина смещения КЦО («центр тяжести»)

AL =

^D 12 ^a

2(cos² c + b sin² c )

где коэффициенты a , b , c определяются следующим образом:

1 - m о a =----cos 6, b =

1 + m

1 - m

1 + m

2 nA d c =-----

^ к

10) координаты КЦО ( Х КЦО 12 ), образованного УО 1 и УО 2 ,

X 1 + X 2

КЦО12 = 2

+ AL

X 1 X 2

^D 12

После обработки последнего излученного РСН импульса j -й подпачки производится вычисление усредненного X _КЦО за подпачку по формуле

X X КЦО

V _ n = 1

X КЦО =    64

где Х КЦО – положение кажущегося центра отражения БКЩ для n -го излученного импульса РСН.

Модель системы угловой автоматики РСН вычисляет угловое положение антенны РСН в азимутальной плоскости, соответствующее отработанному

усредненному за подпачку положению КЦО ( X _КЦО ).

На рис. 3 приведена упрощенная структурная схема модели СУА РСН по азимуту.

Моделирование звеньев произведено путем численного интегрирования с шагом ( A t ), равным периоду повторения импульсов РСН, умноженному на число импульсов в подпачке. Коэффициент усиления k = 6, постоянная времени Т = 0,5 с.

Угол линии визирования ( ф _ЛВ ) вычисляется по формуле

ф ЛВ = - a sin

^Х КЦО D

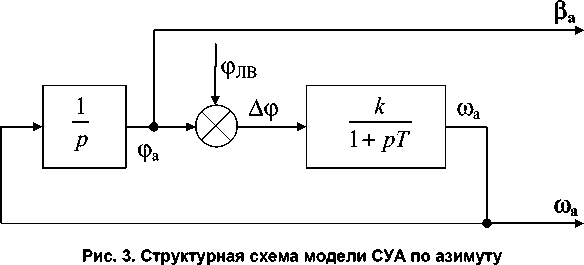
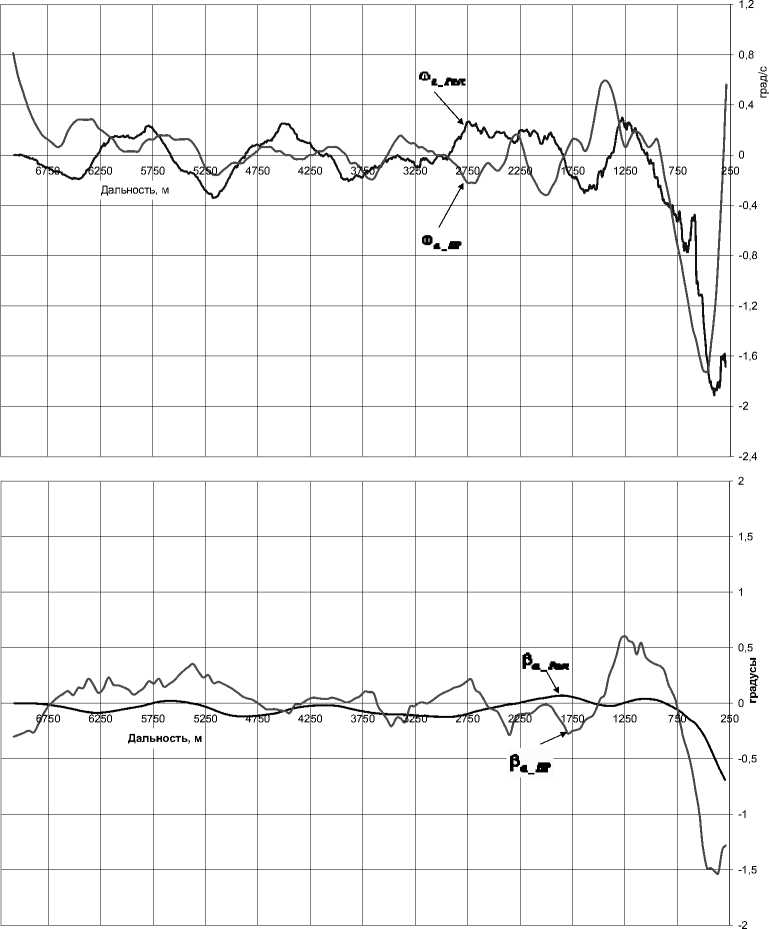
Рис. 4. Изменение углового положения и угловой скорости перемещения КЦО в зависимости от дальности ракета-БКЩ

Переменной D в данном случае обозначена дальность от ракеты до КЦО БКЩ:

Угловая скорость антенны РСН ю _а для j -й подпачки ( ю _а [ /' ]) вычислена как

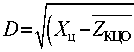
2        „\2             _\2

- X р ) ⁺ ( ^ КЦО - ^ р ) ⁺ ( Z u ⁺ X КЦО - Z p )

® а ^[ j ^] = ® а ^[ j ^{- 1] +} ^ t

k Ф лв ^- k Р а ^[ j ^- 1^] T

^^^^^^е

® а ^[ j ^{- 1]} ■

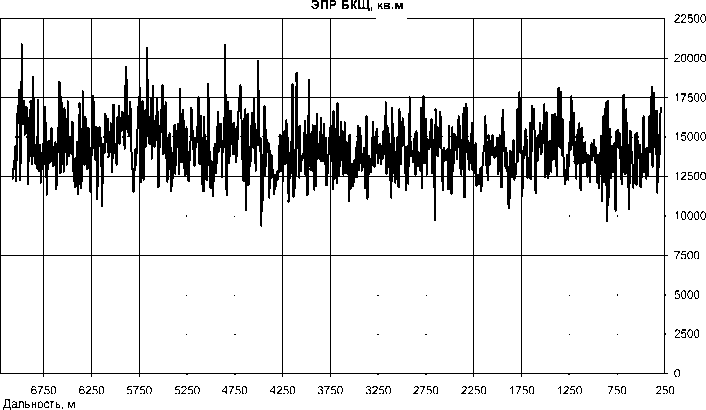
Рис. 5. Зависимость расчетной ЭПР кажущегося центра отражения БКЩ от дальности ракета-БКЩ

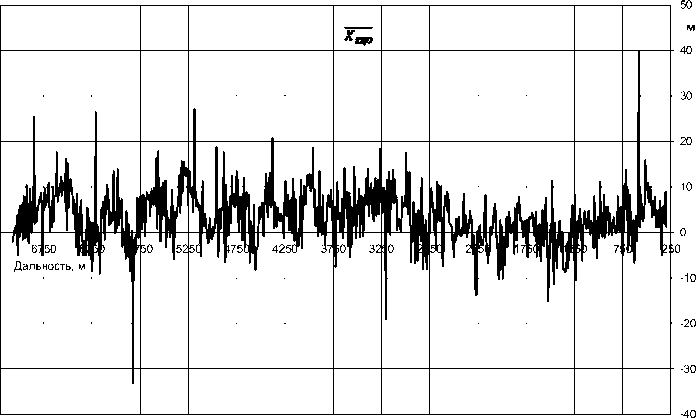
Рис. 6. Зависимость смещения КЦО вдоль продольной оси БКЩ ( X КЦО ) от дальности ракета-БКЩ

Угловое положение антенны РСН по азимуту Р а ( в а [ /' ]) определяется следующим образом:

Р а [ / ] = в а [ / - 1] + А t « а [ / ].

При расчете в а [ / '] и ю _а [ / '] для первой подпачки ( /' = 1) принимается «> _а [ / -1] = в а [ / '-1] = 0, т. е. в начале расчета строительная ось антенны РСН направлена на центр БКЩ (нулевые начальные условия).

Результаты работы программы расчета углового положения, скорости перемещения КЦО и ЭПР БКЩ приведены на рис. 4, 5. На рис. 4 показано изменение углового положения и изменение угловой скорости перемещения КЦО в азимутальной плоскости в зависимости от дальности ракета-БКЩ (расчетные юа[/'] и Ра[/'] обозначены как ®а_расч и ва_Расч). На этом же рисунке для сравнения и подтверждения результатов расчета приведены эти же параметры юа и Ра, взятые из телеметриче ской информации (юа_нР и ва_НР) с натурной работы ракеты (прямолинейный подлет ракеты перпендикулярно продольной оси БКЩ на конечном участке траектории).

На рис. 5 приведена зависимость расчетной ЭПР кажущегося центра отражения БКЩ в зависимости от дальности от ракеты до БКЩ.

На рис. 6 приведена зависимость смещения КЦО вдоль продольной оси БКЩ ( X _Кц_О ) от дальности от ракеты до БКЩ.

Выводы

Проведена оценка характеристик для мишени типа БКЩ пр. 436-бис при прямом подлете ракеты с дальности 7 км, перпендикулярно продольной оси мишени. Амплитуда флюктуаций КЦО вдоль продольной оси БКЩ в среднем составила ± 15 м относительно центра БКЩ. Среднее значение ЭПР

БКЩ составило порядка 15 000 м². Сравнение графиков на рис. 4 указывает на схожесть полученных результатов и результатов натурной работы. Например, значение дисперсии для ю _а__Расч составило 0,14 ( ° /с)², для ® _а_нР — 0,16 (°/с)². Математическое ожидание для ю _а__Расч составило -0,05 ° /с, для ш _{а НР} составило -0,08 °/с.

Разница в значениях дисперсии и математических ожиданиях связана с неточностью принятых моделей, возможным несовпадением фаз сигналов в реальной РСН с расчетным набегом фазы в модели БКЩ и отсутствием учета отражений от морской поверхности. Также дополнительный вклад в разницу математических ожиданий вносит имеющаяся статическая ошибка СУА реальной РСН. В целом принятая модель позволяет достаточно достоверно оценить радиолокационные характеристики БКЩ.

Намечен путь по улучшению разработанной программы расчета ЭПР, углового положения и скорости перемещения КЦО мишени, заключающийся в разработке модели системы управления ракеты по курсу (на рис. 1 – блок, обозначенный пунктирной линией). Это позволит выбирать раз- личные пути подлета ракеты к БКЩ, а также корректировать курс полета ракеты в зависимости от изменения юа, выдаваемого РСН в бортовую аппаратуру ракеты.