Оценка распределения температуры в локальной приконтактной зоне при свободном ортогональном резании

Введение. Основная задача, решаемая в рамках настоящей работы, состоит в том, чтобы показать, как, опираясь на методы формального описания процессов теплопередачи и решения краевых задач теплопроводности, проводить теплофизический анализ процессов, происходящих в технологических системах обработки материалов под действием внешних и внутренних источников (стоков) теплоты. Целью этого теплофизического анализа является определение путей, методов и средств повышения эффективности технологических систем и качества производимых изделий.

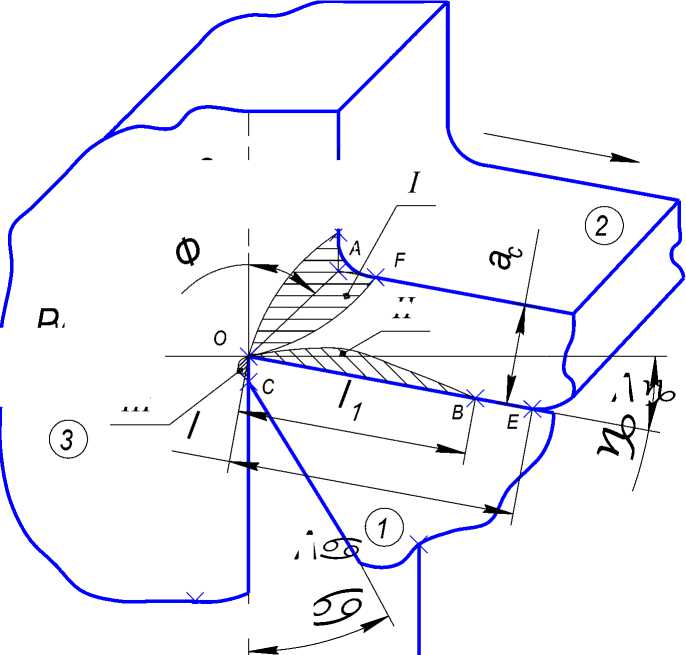
Независимо  от конкретной цели теплофизического  анализа и определяемой информации, а также от конкретного вида технологической системы, анализ проводят в определенном порядке, который можно представить в виде обобщенного алгоритма [1]. Теплофизический анализ целесообразно начать с рассмотрения схемы теплообмена при работе простым единичным режущим клином (схема свободного ортогонального резания). Эта схема имеет одно движение (главное движение резанья Dr с постоянной скоростью V) и допускает плоское представление (рис. 1). Физическая модель свободного ортогонального резания. Источники тепловыделения [2]:

V c

A

II

A

A

I

V (Dr)

a

E

III

u

(IV)

Рис. 1. Физическая модель свободного ортогонального резания (контактирующие твердые тела: 1. инструмент; 2. стружка;

• 3.    заготовка)

• I.    Зона первичных сдвиговых деформаций (OEF), которая в моделях стружкообразования первого приближения может быть представлена в виде единичной плоскости сдвига ОА;

• II.    Зона вторичных деформаций на прирезцовой поверхности стружки (тонкий пластический деформируемый слой);

• III.    Зона пластических деформаций в поверхностном слое заготовки, примыкающем к задней поверхности Аα инструмента. Структура этой зоны в основном подобна структуре зоны II, касательные и нормальные напряжения распределены аналогично. Протяженность зоны III при работе

острозаточенным инструментом значительно меньше протяженности зоны II.

• IV.    Дополнительные источники энергии, поступающей в зону резания (электроконтактный подогрев, нагрев плазмой, ТВЧ, лазером и т. п.).

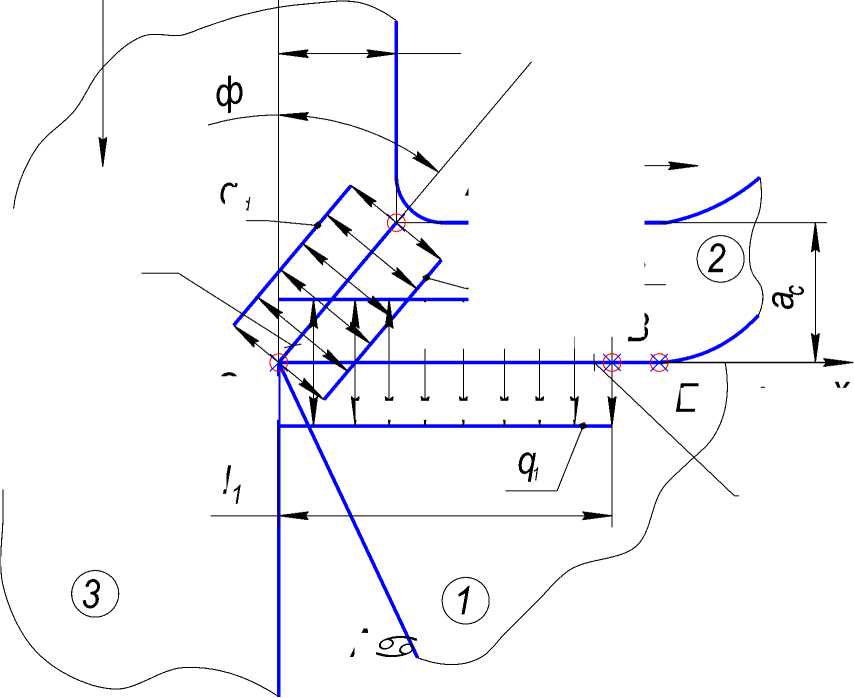
Сделаем следующие упрощения в физической модели зоны резания (рис. 2):

• 1)    Зону первичных деформаций I представим в виде единичной плоскости сдвига ОА (граница раздела между заготовкой 3 и стружкой 2);

• 2)    Пренебрегаем влиянием зоны III (площадь контакта инструмента с заготовкой по задней поверхности инструмента считаем равной нулю);

• 3)    Источники тепловыделения на площадке ОА (зона I) и ОВ (зона II), считаем распределёнными равномерно.

Поверхностная плотность источника тепловыделения в зоне первичных деформаций I:

W′ 2 = О деф + Ч э1 = Ч 2д +Ч 2с = (1-b*) W'₂ + b*W'₂ ,                     (1)

• где О деф - поверхностная плотность источника тепловыделения от пластических сдвиговых деформаций в зоне I;

д_э 1 - поверхностная плотность источника тепловыделения, обусловленная подводом дополнительной энергии (электроконтактный подогрев) в зоне I;

д_2д = (1-b*) W / - поверхностная плотность теплового потока, поступающего в заготовку (тело 3) через площадку ОА;

q2c=b*W'2   - поверхностная плотность теплового потока, поступающего в стружку (тело 2 ) через площадку ОА;

b* - коэффициент распределения тепловых потоков на условной плоскости сдвига ОА.

V

y

a

B

l q2d .

E

A

Рис. 2. Упрощённая физическая модель зоны резания (первичная подсистема ТС обработки лезвийным инструментом).

Vc A

q 2c          ^q2

O

V V V V V V V

A ^

В

q деф = τ s Vсдв = Vτ s cos γ/ cos (Ф - γ).                                     (2)

q э1 = I²R 1 / f сдв ,                                                                             (3)

где R1 – электрическое сопротивление зоны I;

I – электрический ток;

fсдв = ab/sin Ф – площадь сдвига (b – ширина среза).

Поверхностная плотность источника тепловыделения на площадке контакта инструмента со стружкой (зона II)

W' i = q i + q 2 = q mp + q э2 = (1- X ) Wy + X W ,                           (4)

где qтр – поверхностная плотность источника тепловыделения от сил трения (внутреннего и внешнего) на передней поверхности инструмента;

Qэ2 - поверхностная плотность источника тепловыделения, обусловленного подводом дополнительной энергии к зоне II;

q₁ = (1- x )W / - поверхностная плотность теплового потока, поступающего в инструмент через площадку ОВ (считаем, что В = Е и 1 1 - 1 );

q₂ = X W / - поверхностная плотность теплового потока, поступающего в стружку со стороны передней поверхности через площадку ОВ (итоговый поток теплообмена);

X - коэффициент распределения теплового потока на передней поверхности инструмента (неизвестен, будет определен решением соответствующего балансового уравнения).

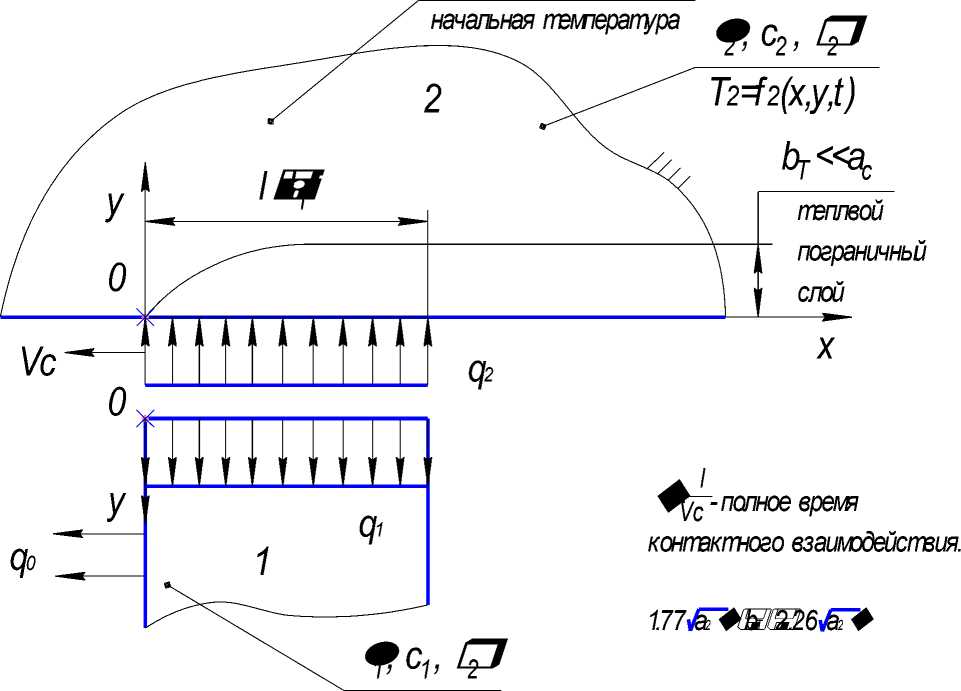
Структурная схема теплообмена в системе контактирующих тел представлена на рис. 3.

Тело 1 (инструмент): полуограниченный стержень, нагреваемый с торца тепловым потоком плотностью q₁; на свободных поверхностях стержня идет теплообмен с окружающей средой по закону Ньютона Q₀=a₁(T₁-T_oc); стационарный тепловой режим.

Тело 2 (стружка): полупространство с адиабатической границей; на поверхности действует движущийся источник тепловыделения с поверхностной плотностью q₂; нестационарный тепловой режим.

В построенной структурной схеме теплообмена тела 3 (заготовка) исключено из рассмотрения. Влияние источников тепловыделения, расположенных в зоне первичных деформаций, учитываем, считая, что начальная температура в теле 2 равна

То= Тос + Т 2с ,                                                  (5)

где Тос - температура окружающей среды (для упрощения анализа полагаем Тос = 0);

T o =T oc +T 2c

T1=f1(y)

Рис. 3. Структурная схема теплообмена в системе контактирующих тел

Т2C – температура в стружке после прохождения зоны первичных деформаций I (распределена равномерно по сечению стружки).

Т 2C = (Q c ) /( W c c 2 ρ 2 ),                                                           (6)

где Qc – доля мощности источников тепловыделения, расположенных в зоне I, поступающая в стружку;

c2,  ρ2  – удельная теплоёмкость и плотность материала заготовки, соответственно;

W c = Vab – объём стружки, образуемой за единицу времени.

Краевая задача теплопроводности для тела 2  (стружка).

Температурное поле в теле 2 (рис.4)

Т 2 = f 2 (x,y,t) = T o + T 2п (x,y,t),                                                (7)

где T_2п (x,y,t) – приращение температуры за счёт действия подвижного источника с поверхностной плотностью q 2 .

Источник q2 считаем быстродвижущимся, т.е.

Ре = V с l /a 2 ≥8…10.

Это означает, что распространением теплоты перед движущимся источником можно пренебречь и считать, что теплота распространения только по нормали к прирезцовой поверхности стружки.

Формализованная физическая модельy тела 2 ( неподвижное полупространство)

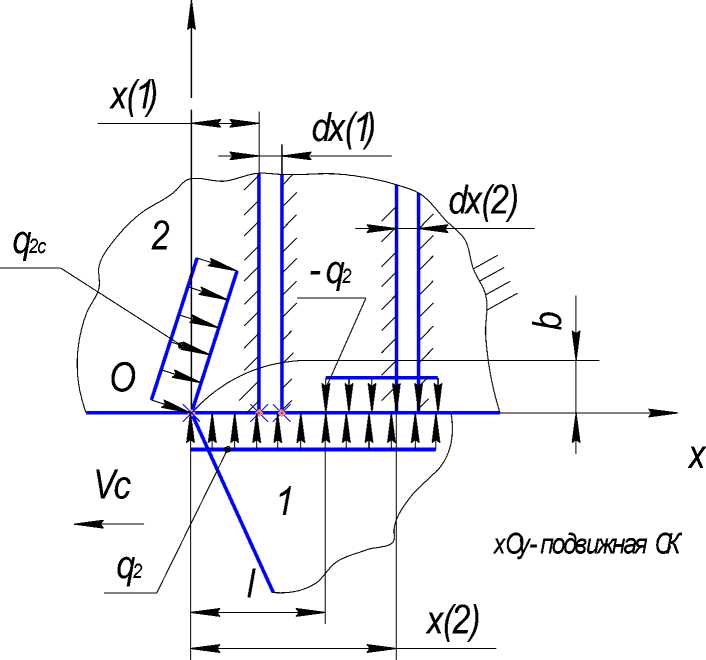
Рис. 4. Формализованная физическая модель тела 2 (неподвижное полупространство)

Такое допущение позволяет представить полупространство как пакет полуограниченных стержней толщиной dx, имеющих адиабатическую изолированную боковую поверхность, и свести задачу к классу задач одномерной нестационарной теплопроводности.

Элемент dx ( ₁ ) можно рассматривать как полупространство, нагреваемое постоянным тепловым потоком q 2 , действующим в течение времени (текущее время контактного взаимодействия)

t' = х / V c (0≤ t' ≤τ =l/V c ).

Для элемента dx ( ₂ ) при t^/>τ добавляется дополнительный фиктивный сток теплоты с поверхностной плотностью – q 2 и временем действия

И X -1 I t =----= t 7 - T

V c

Для описания «моментального снимка» температурного поля в теле 2 в подвижной системе координат хОу, который будет воспроизводиться в каждый текущий момент t при установившемся процессе стружкообразования, можно использовать решение задачи нагрева полупространства поверхностным импульсным источником постоянной мощности.

Это решение в нашем случае имеет вид :

- при 0≤ х ≤ l    (0≤ t' ≤τ);   0≤ у <∞:

Т 2 = Т 2 П ( X , y ) + Т 0

x q2  a2

c

^

ierfc

2 a

y

- x/ ⁺ T0

c

x q2  a2

c

^

f 1

"7= е

n

V

y 2 V c 4 a ₂ x

—

y

2 a^x

erfc

2 a

V _c

A

y

• x/

2 /V

/ c 7

⁺ T 0 ;

при х> l (t^/>τ); 0≤y<∞:

T

Т ₂

2 q a

^ 2

^^

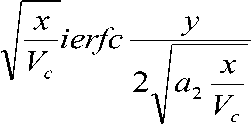
x — l

V c

ierfc

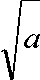
x — l

V c

y

^{+ T} 0 ^. (9)

Краевая задача теплопроводности для тела 1 (инструмент). Тело 1 рассматриваем как полуограниченный стержень без тепловой изоляции. Конец стержня (у = 0) нагревается постоянным тепловым потоком с поверхностной плотностью q1 = (1-χ) W'1, на свободных поверхностях стержня идёт теплообмен с окружающей средой по закону Ньютона q0= α(Т1-Тос) = αТ1 (считаем Тос = 0).

Математическая     формулировка     задачи     стационарной теплопроводности для тела 1:

∂ T 1 _{= a} ∂ ² T 1 ₊ q v 1 _{= 0}

∂ t       ∂ y 2     c ρ     ,                       (10)

λ 1

где а1 =    – коэффициент температуропроводности материала тела c1ρ1

1;

qv1 – объёмная плотность источника теплопоглощения, учитывавшего конвективный теплообмен с окружающей средой на свободных поверхностях стержня.

dQ qV1= dW , где dQ=-αT1Pdy – мощность теплообмена на боковых поверхностях элемента стержня длиной dy (P – периметр сечения стержня);

dW=Fdy – объем элемента стержня длиной dy (F – площадь сечения стержня).

α T

δ = ^F P ^.

Таким образом, q v 1 = -      , где

С учетом этого дифференциальное уравнение теплопроводности

принимает вид:

d2T1(y)   α

-

dy ²

T1(y)=0 или d T1 dy2

- m 2T = 0,

где m 1

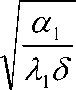
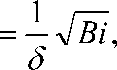
. Ri = 01

где Bi - р критерий Био.

Граничные условия (І-го рода):

• а)    Т₁(0)=Т_1К (температура контактного конца стержня);

• б)    Т 1 (∞)=0.

Общее решение линейного однородного уравнения стационарной теплопроводности:

Т ( y ) = Ae my + Be - m y .

Постоянные интегрирования A и B определяем из граничных условий:

• б)    y→∞:       А=0;

• а) y=0:           В=Т 1К.

После подстановки постоянных интегрирования решение примет вид:

- V Bi . y

Т 1 ( y ) = T 1 K e - m ¹ y = T 1 _K e    ⁵

Для определения Т 1К используем уравнение

qi = (1 -X)W; = -Л ^Т1(0) = ZimiTiк.

dy

Согласование решений, полученных для тел 1 и 2, и определение коэффициента распределения теплового потока % . Балансовое уравнение:

2 max

= т i к,

2Wi/XT  (i - х )Wi/ yj ПЛ Ср рг     Zimi

Коэффициент распределения теплового потока:

У пЛc ₂ P 2 W - T ₂ Лт) W_v¹ (2\m_v T + 4 пЛ c₂ P )

С целью упрощения в последней формуле целесообразно пренебречь

Т 2с , тогда

χ =

1 + 2

V ^пЛ 2 c 2 ^p 2

Таким образом, получив зависимость для расчёта коэффициента распределения теплового потока на площадке контакта инструмента со стружкой по передней поверхности χ, мы определили последнюю неизвестную величину, входящую в формулы для расчёта температурного поля в корректирующих телах 1 (инструмент) и 2 (заготовка), а также распределение поверхностной температуры на площадке контакта. Задачу теплофизического анализа процесса обработки единичным режущим клином (схема свободного ортогонального резания) можно считать решенной. Полученные расчётные зависимости являются замкнутыми и не содержат неизвестных величин.

В заключение сделаем два общих замечания:

• 1)    Разработанный алгоритм расчёта температурных полей в контактирующих телах может быть представлен в виде программы для ЭВМ, что позволяет существенно ускорить проведение расчетов при решении конкретных задач теплофизического анализа процесса обработки лезвийным инструментом.

• 2)    Рассмотренная методика теплофизического анализа не содержит каких-либо ограничений на вид и количество контактирующих тел в системе, характер контакта между ними и природу источников теплообразования; поэтому изложенная методика является, в принципе, применимой к любым технологическим системам или их подсистемам

независимо от того, какие рабочие процессы осуществляются в этих системах (обработка ППД, шлифование и т.д.).