Оценка размеров области загрязнения естественных грунтовых вод инфильтрационным потоком

The task about movement of ground waters in the interfluves massif of soil in the presence of an infiltration food from an earth surface is described in article.

This task is actual as rather often meets in engineering practice.

Орлов В. Т., Зайцев О. И., Локтионова Е. А. Оценка размеров области загрязнения естественных грунтовых вод инфильтрационным потоком. /

The simplest scheme of the solution of tasks about movement of ground waters - model use gradually changing movement at which live sections of a stream can be considered vertical and flat is submitted, and the average speed of a filtration in section can be determined on Dupuis's formula.

Задача о движении грунтовых вод в междуречном массиве грунта при наличии инфильтрационного питания с поверхности земли (рис. 1) достаточно часто встречается в инженерной практике. Обычно целью решения этой задачи является определение положения депрессионной поверхности и величины фильтрационного расхода q, который зависит не только от расхода естественных грунтовых вод q e , но и от плотности инфильтрационного питания ε и её распределения по поверхности.

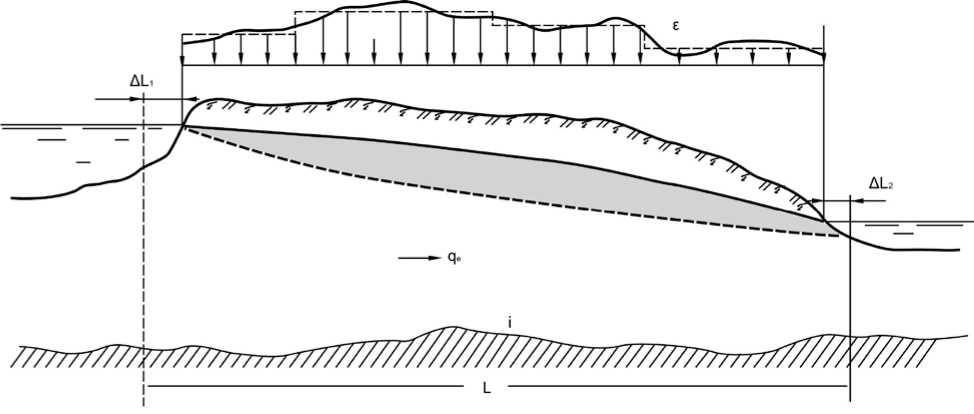
Рис. 1. Задача о движении грунтовых вод в междуречном массиве грунта при наличии инфильтрационного питания с поверхности земли

Вместе с тем в случае инфильтрации с поверхности загрязнённой жидкости, практически не отличающейся по плотности от грунтовой воды, важно знать размеры области загрязнения потока. В первом приближении оценку границы области загрязнения может дать положение раздельной линии тока (на рис. 1, 2 показана пунктиром), ниже которой находится часть естественного потока из одного водоёма в другой, а выше неё — часть потока, обусловленная инфильтрационным питанием. Конечно, такая граница раздела соответствует только так называемому конвективному переносу (или поршневому вытеснению) загрязнения, и концентрация примеси на ней меняется скачкообразно. В действительности эта граница раздела размывается за счёт фильтрационной дисперсии, и концентрация изменяется непрерывно. Однако решения уравнений фильтрационной дисперсии имеются главным образом только для простейших фильтрационных течений [3, 7, 8]. В силу этих причин использование раздельной линии тока вполне приемлемо для предварительной оценки положения границы области загрязнения.

Наиболее простой схемой решения задач о движении грунтовых вод является использование модели плавноизменяющегося движения, при котором живые сечения потока можно считать вертикальными и плоскими, а среднюю скорость фильтрации в сечении можно определять по формуле Дюпюи [1, 2, 3, 4, 5, 6]. При использовании этой модели несовершенство водотоков или водоёмов в фильтрационном отношении учитывается введением фильтрационных сопротивлений в виде дополнительных участков длиной ∆ L ₁ и ∆ L ₂ (рис. 2) [9, 10]. В случае переменной плотности инфильтрационного питания функцию ε ( x ) заменяют кусочно постоянной, разбивая весь массив на фрагменты с постоянным значением ε [7, 9].

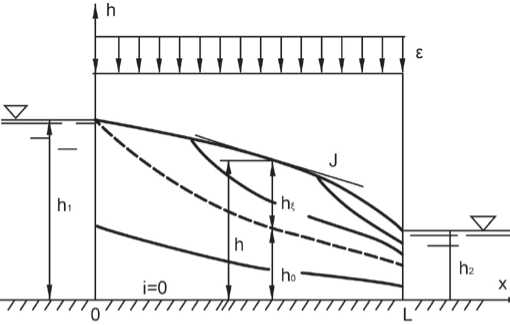
Рис. 2. Расчетная схема

Орлов В. Т., Зайцев О. И., Локтионова Е. А. Оценка размеров области загрязнения естественных грунтовых вод инфильтрационным потоком. /

В простейшем случае расчётная схема представляет собой прямоугольный массив грунта с коэффициентом фильтрации k на горизонтальном водоупоре (i = 0) с постоянной плотностью инфильтрации е (рис. 2). Глубины воды в верхнем и нижнем бьефах равны соответственно hl и h2. Будем принимать длину прямоугольного массива L такой (например, L / h1 > 5 [1]), чтобы высотой промежутка высачивания в нижнем бьефе при любых соотношениях h 2 / h 1 >  0 можно было пренебречь.

Применительно к этой схеме уравнение движения грунтовых вод можно записать в виде [1, 2, 3, 4]

dq     d   dh

— = - k h = е , dx     dx ( dx J

где h (x) — глубина воды в сечении x.

При граничных условиях: 1) h (0) = h1, и 2) h (L) = h2 в качестве решения получим [4, 5, 6]

и

h ²( x ) =

h 1 ²( L - x ) + h 2 x

L

е

+ k (L — x) x

q (x ) = k

( h i^{2 - h} 2 )

2 L

( L

-е - x

Уравнение (2) позволяет построить кривую депрессии, которая представляет собой часть эллипса, а формула (3) даёт величину удельного фильтрационного расхода в любом живом сечении. Из формулы (3) можно получить величину расхода q0 во входном сечении (x = 0), который постоянен по длине в части потока ниже раздельной линии тока

( ^h i2 ^{- h}I ) e L q ⁰        2 L      2 .

Таким образом можно теперь записать

dh q (x) = qQ +e x = - kh .

0            dx

Представим глубину потока h (x) в виде суммы (рис. 1)

h (x) = ho( x) + he (x), где h0 (x) — глубина воды под раздельной линией тока; he (x) — глубина воды над раздельной линией тока.

Теперь из выражения для расхода

q ⁽ х ) = q о +е х = ^- kh o dx - kh е ^^

можно получить hе = h -—eh—- h0 = h - h = h—q0— (q0 +еx) и 0 е qо +еx

.

Из формулы (4) можно найти значение предельной плотности инфильтрации е п, при которой q0 = 0, т. е. вода из верхнего бьефа не поступает в грунтовый массив (h0 = 0)

е

п

^k ( h i ²

^{- h2} )

L ²

Орлов В. Т., Зайцев О. И., Локтионова Е. А. Оценка размеров области загрязнения естественных грунтовых вод инфильтрационным потоком. /

При этом раздельная линия тока совпадает с вертикальным входным сечением и водоупором. Величина расхода q0 может быть представлена в виде q0п=(£ — e)2.

Далее будет рассматриваться течение при ^е-^е п . При ^e > ^ положение раздельной линии тока известно [4, 5, 6]. В этом случае расход воды, обусловленный инфильтрацией, поступает как в нижний бьеф, так и в верхний, и эти доли расхода легко определяются. При этом загрязнённые поверхностные воды будут поступать через всё живое сечение как слева, так и справа. В частном случае при h1 = h2, когда уровни воды в обоих водоёмах одинаковы, раздельная линия будет представлять собой горизонтальную прямую, а загрязненные воды будут поступать в оба водоёма на их поверхность.

Известное уравнение кривой депрессии (2) можно представить в виде

2 q

)2 — —— x

1 k

—

e 2

x 2 . k

Если ввести безразмерные соотношения

h(x) -h(xУ - x - e h = h'x); x = L: = = k: =п

^£ п ^k и

e e m = — = —,

^£ п     ^£ п

тогда уравнение кривой депрессии (2) можно записать как

где

h ( x ) = V1 — ax — bx ² ,

a = ^L (		г 1 _ 1	f h 2 Г"
h 12	i mi —	L	. h 1 )	( I m ) ,

_h  e l ²

b = — m = h 1²

1 —

h ₂ h 1

to.

Таким образом, уравнение раздельной линии тока можно представить в виде в соответствии с (7)

h₀ (x ) = 7 q^k—h(_x \

0 ( ) (q0/k + ex) ( ), причём, используя (9), можно получить соотношение q 0/ k    =    (1— m)

( q о / k + e x ) ( 1 — m + 2 x m )

Имея уравнение раздельной линии тока в безразмерном виде

^h о ( ^x ) =

-(1— ^m)_ V1 — ax — bx ², — m + 2 x m )

Орлов В. Т., Зайцев О. И., Локтионова Е. А. Оценка размеров области загрязнения естественных грунтовых вод инфильтрационным потоком. /

h                                                                   £ можно, задавая отношение глубин — и относительную интенсивность инфильтрации ю = —, hi                                                                                £ п построить раздельную линию тока в прямоугольном грунтовом массиве.

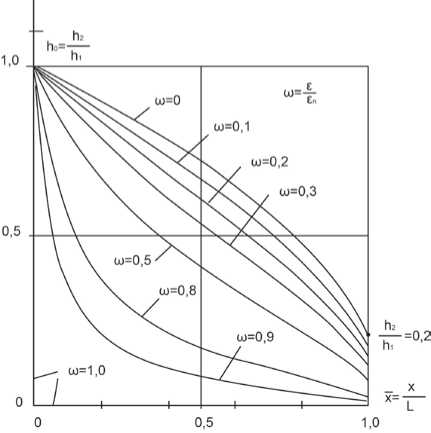
Рис. 3.

В качестве примера на рис. 3 приведены в безразмерной форме раздельные линии тока при h

— = 0,2 для различных относительных интенсивностей инфильтрационного питания ю< 1..При h1

отсутствии инфильтрации ( ю = 0 ) раздельная линия тока совпадает с кривой депрессии, тогда как при ^ю >  ⁰ кривая депрессии вообще не является линий тока.